构造等时三角形 巧解直线运动题
郑 金
(辽宁省凌源市职教中心,辽宁 朝阳 122500)
对于物体在竖直平面内的直线运动问题,有时可通过构造等时三角形,利用自由落体运动规律求解,巧妙快捷。
1 等时三角形的构建
如图1所示,在半径为R的竖直圆环内,放置几个光滑的直轨道,其一端位于圆环的最高点A或最低点B,另一端在圆环上。应用运动学公式可以证明:若两个小球同时从最高点A由静止沿不同的轨道下滑,会同时到达点C、D。若两个小球同时从点C、D由静止开始沿不同的轨道下滑,会同时到达最低点B。而且下滑运动经历的时间与各弦的倾斜程度和长度无关,都等于小球从圆周的最高点自由下落到最低点经历的时间。
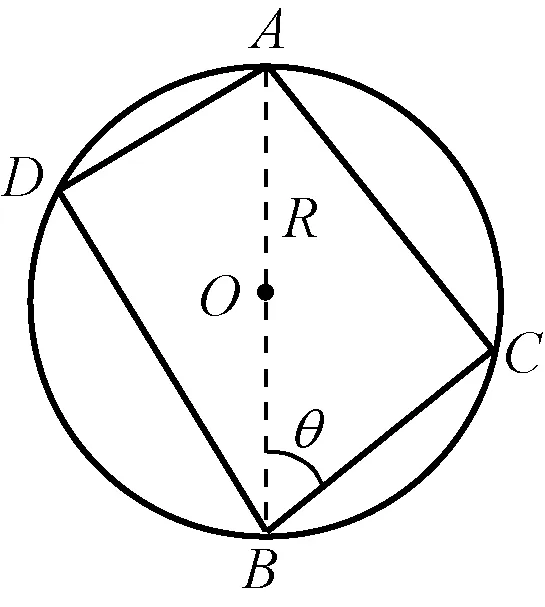
图1
2 应用实例
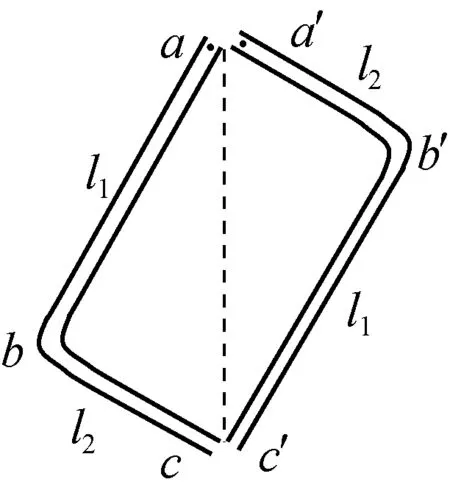
图2
例1:如图2所示,两个完全相同的光滑直角弯管abc和a′b′c′,摆放成矩形固定放置,一条对角线沿竖直方向。有两个完全相同的小球A、B分别从两个弯管的上端管口由静止滑下,假设小球在直角转弯处无机械能损失,两球到达出口c和c′处经历的时间分别为t和t′,则( )。
A.t=t′ B.t>t′
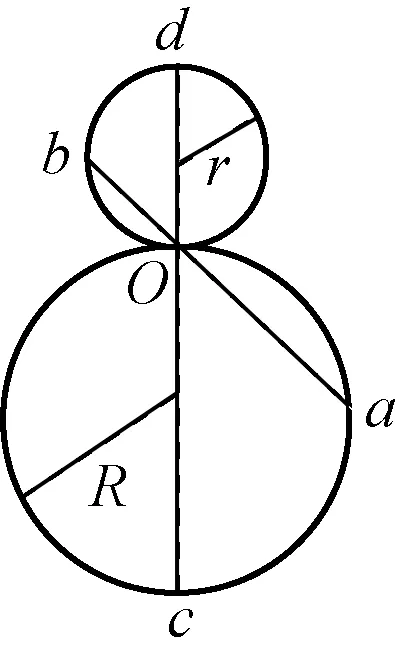
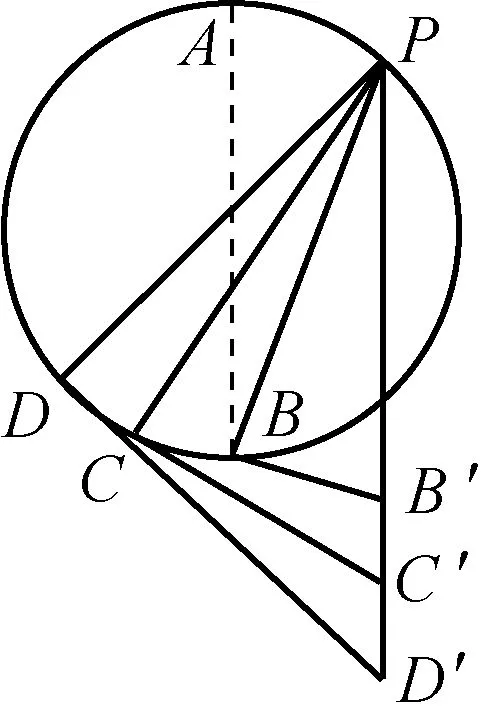
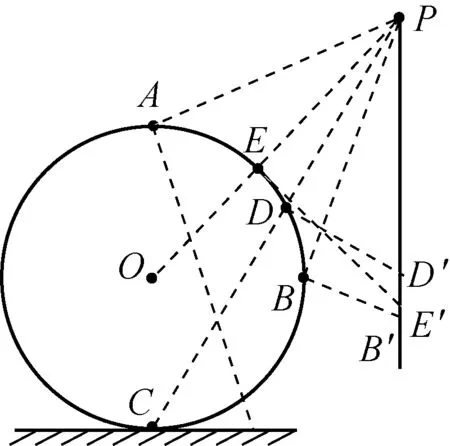
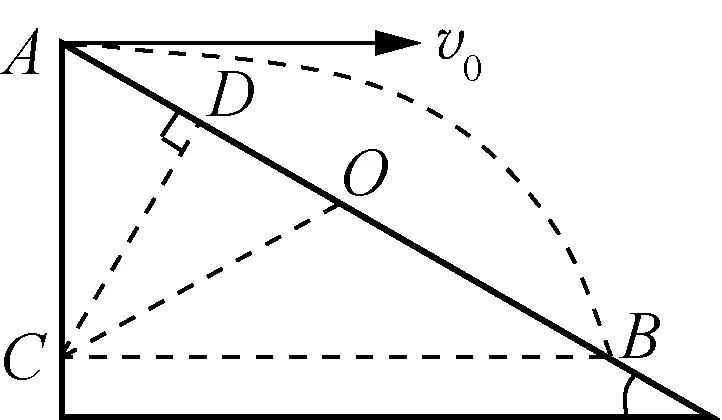
C.t 图3 解析:由于直角弯管的内壁光滑,且到达转弯处无机械能损失,由机械能守恒定律可知:两球到达出口处的速率相等,则速度图像的末端位于同一水平线上。由于两球通过的路程相同,则图像与横轴围成图形的“面积”相同。两个小球在l1段的加速度a1相同,在l2段的加速度a2也相同,且a1>a2,因此图像为折线。由于直角三角形的斜边沿竖直方向,可知小球从两个弯管的最高点下滑到转弯处经历的时间相同,则两条折线拐点位于同一平行于速度轴的直线上。速率-时间图像如图3所示,可知小球先从左侧弯管下端掉出,即t 例2:如图4所示,半径分别为R和r的圆环竖直放置,一条公共弦过两圆的切点、且分别与两圆相交于a、b两点。在此弦上铺一条光滑轨道,令一小球从a点以某一初速度沿轨道向上运动,设小球恰好能到达b点,则该小球从a点运动到b点所用的时间为多少? 图4 图5 解析:因小球恰能上升到b点,即到达b点时速度为零,则根据运动的可逆性,可把小球由点a向b的匀减速运动等效为由点b向a的匀加速运动,这样就能利用等时性解题了。 对于在竖直平面内的两个外切的圆而言,小球沿过切点的公共弦从上端由静止滑到下端的时间等于小球从一个圆的最高点由静止下落到另一个圆的最低点经历的时间,这与等时圆的特性相似。 例3:如图6所示,PB、PC、PD是竖直平面内三根固定的光滑细杆,细杆两端都位于同一圆周上,A为圆周最高点,B为圆周最低点。每根细杆上都套着一个小环,三个小环都从P点无初速释放,用t1、t2、t3依次表示小环沿细杆运动到点B、C、D所经历的时间,试比较t1、t2、t3的大小。 图6 图7 解析:如图7所示,过P作竖直线,以竖直线为斜边,分别以PB、PC、PD为直角边作直角三角形,可知对应的斜边长度不等,那么对应自由落体运动的时间不等,易知t1 图8 例4:如图8所示,圆环和点P在同一竖直平面内,在环上取一点与P连成光滑直轨道,一物块由静止开始从P点滑向圆环。A是圆环的最高点,B是圆环的最右端,C是圆环与地面的接触点,D是PC与环的交点,O为圆心,E是PO与环的交点,物块滑到圆环上所需的最短时间为( )。 A. 沿PA轨道运动的时间 B. 沿PB轨道运动的时间 C. 沿PD轨道运动的时间 D. 沿PE轨道运动的时间 图9 解析:如图9所示,过点P画一竖直线,以此作为斜边,再分别以PA、PB、PD、PE作为直角边,构造直角三角形,可见:过D的直角三角形的斜边PD′最短,则沿PD轨道运动的时间最短,选项C正确。 图10 图11 虽然等时三角形与等时圆是等效的,但在作图时,利用等时三角形比较简单,不必再作圆了。而直接利用等时三角形解答有关问题,只需定性分析,不必定量推导,显得直观简便。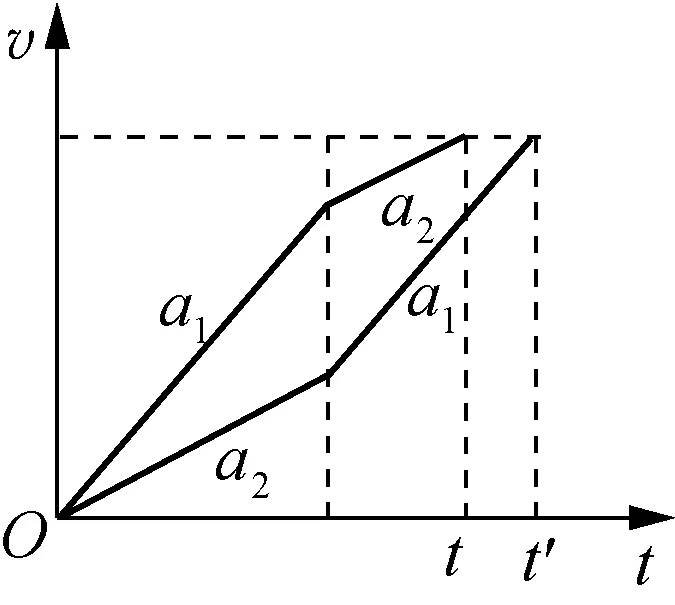
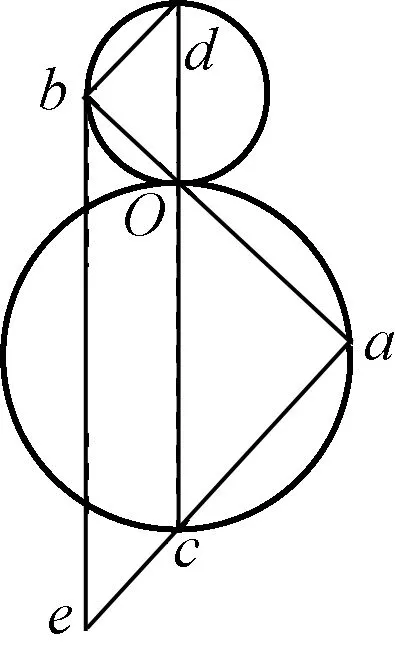





3 结语

