应用Geogebra软件突破几何光学教学难点

孙宁波 袁海泉

(苏州大学物理科学与技术学院,江苏 苏州 215006)

1 引言

信息技术与物理教学的深度融合是提升学生核心素养的有效手段，Geogebra作为一款结合几何、代数、图形、统计和计算的动态数学软件,有着开源、免费、操作简单等诸多优点。[1]笔者以几何光学为例,阐述Geogebra在教学中的应用,厘清课件原理,讲明操作步骤,简要说明学生应用该软件的探究流程。

2 Geogebra在几何光学中的应用

2.1 从光的折射到全反射的动态变化模拟

2.1.1 难点分析

理解光线发生全反射的条件是本节课的难点,但教材受限于呈现形式,只能给出光线发生全反射时的静态图像,学生难以清晰地认识光线从折射到全反射的动态变化,从而造成学生对全反射的理解困难。

2.1.2 突破方法

以光线的入射角为变量,依据折射定律得到折射角的表达式,利用Geogebra易得折射角随入射角变化的动态折射光线。该课件不仅可以帮学生建立光线发生全发射的动态模型,而且能够对每一个状态进行分析,从而深化学生对全反射的理解。

2.1.3 课件制作

(1) 如图1所示，输入“线段[(0,0),(20,0)]”得到线段a,用“描点”工具单击线段a得到点O,再运用“垂线”工具得到过点O且垂直AB的垂线g。

图1

(2) 输入“圆弧[(10,0),(0,0),(10,4)]”得到圆弧c,运用“描点”工具在圆弧c上除A、D两点外的其他位置单击,得到点S。

(3) 输入“射线(O,S)”,利用“角度”工具得到射线OS和垂线g的夹角α。

(4) 点击“滑动条”,创建变量n,设置其最大值为2,最小值为1,输入γ=arcsin((sinα)*n),k=tan(90°-γ),y=k*(x-10)，得到函数图线p。

(5) 通过“轴对称”工具得到射线OS关于垂线g的对称图线h。

2.1.4 课件说明

点S是光源,滑动条n代表介质n的折射率，拖动点S或右键单击“启动动画”,可以看到折射光线随入射角增大而逐渐偏离法线的动态过程,在折射光线与界面AB重合的瞬间,折射光线消失,只剩下反射光线,这就实现了从光的折射到全反射的动态变化模拟。拖动滑动条,改变n值,还可以比较光线在不同介质中发生折射和全反射的情况。

2.2 白光的三棱镜色散现象模拟

2.2.1 难点分析

在人教版高中物理选修2-3中,仅简要介绍了三棱镜的色散,而在实际教学中,学生会对色散后的色光分布、影响偏向角大小的因素等认识不清,而传统的作图分析难以使学生动态地观察到光的色散过程,不利于对色散和偏转角进行定量分析,这导致学生难以深入认识光的色散现象。

2.2.2 突破方法

以入射角为变量,依据折射定律算出对应的折射角,再利用图中的角度关系绘出棱镜内的折射光线,并将其作为下一次的入射光线,重复上述过程,得到出射光线,实现棱镜内折射光线和出射光线跟随入射光线偏转的动态效果，不仅能够直观地演示该过程,而且还能对色散现象进行定量的阐释和分析。

2.2.3 课件制作

(1) 利用“多边形”工具画出等边△ABC,利用“垂线”工具过B点作AC的垂线f,再利用“交点”工具作出垂线f与AC的交点D。

(2) 单击“滑动条”,创建变量a,设置最大值为3,最小值为-3.5,输入(0,a)创建动点E,输入“直线(D,E)”得到直线m,再利用“角度”工具作出m与f的夹角α。

(3) 单击“滑动条”创建变量n,设置最大值为2,最小值为1,依次输入α1=arcsin((sinα)/n),k1=-tan(30°-α1),(y-1.29)/(x-2.74)=k1,作出直线j,再利用“夹角”工具画出j和f的夹角α1。

(4) 重复上述过程,得到出射光线，展示三棱镜对不同色光的偏折(图2)、三棱镜对入射角不同的单色光的偏折(图3)。

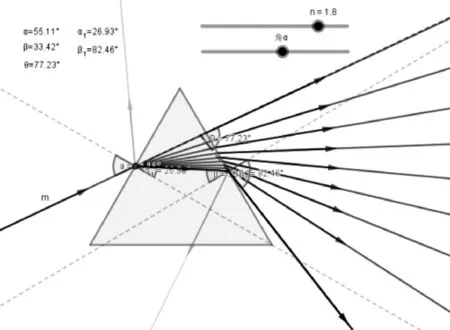
图2

2.2.4 课件说明

滑动条n的数值代表三棱镜对色光的折射率,改变n的数值,可以比较三棱镜对不同色光的偏折程度,并用来说明色散现象,如图2所示,从上到下的出射光线依次代表折射率为1～1.8的色光的偏折情况,当折射率为1.9时,在三棱镜右界面发生全反射。滑动条角α代表入射角的大小,改变α可以比较入射角变化时,出射光线的偏折情况,图3中θ代表偏向角的大小,从上到下的出射光线依次代表入射角改变6°时的偏折情况。

图3

2.3 凸透镜成像规律的动态表达

2.3.1 难点分析

在人教版高中物理选修2-3中介绍了“探究凸透镜成像规律”实验和“透镜成像作图法”,学生进行实验后,一般难以将形象的实验现象抽象成相应的物理模型,从而造成学生对运用“透镜成像作图法”分析透镜成像规律的困难。

2.3.2 难点突破

以物距为变量,运用透镜成像作图法,绘出特殊光线,在Geogebra中易得像的位置,再利用“向量”工具对直线进行修饰,就能得到透镜的动态成像过程，可以帮助学生建构该物理模型,而且还能对物体在任意位置的光路进行定量分析,有助于学生理解凸透镜成像规律。

2.3.3 课件制作

(1) 如图4所示，单击“滑动条”创建变量p,设置最大值为0,最小值为-20,输入(p,0)、(p,3)、(-2,0)、(2,0)、(0,0)，得到点A、B、F、F1、O,输入“向量(A,B)”。

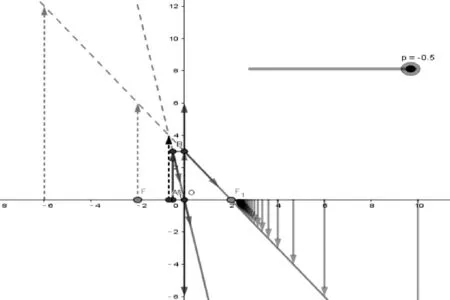
图4

(2) 画出过光心的光路g和平行主光轴的光路m。

(3) 输入“交点(g,m)”得到B1,再利用“向量”工具画出两个相等向量b(A1,B1)、c(A1,B1)。

(4) 在c的脚本中输入“if(p>-2,设置可见性(c,1,false),设置可见性(c,1,true))”,在b的脚本中输入“if(p<-2,设置可见性(b,1,false),设置可见性(b,1,true))”。

2.3.4 课件说明

滑动条p代表物体到透镜的距离,改变p的数值,能够使学生直观地看到像跟随物距变化的动态过程。在教学中,该课件能够通过透镜成像作图，定量分析透镜的成像规律,解决了传统作图、分析繁琐的弊端。此外,课件还可以用来分析物距、像距和焦距之间的关系。

2.4 光学习题的情景再现

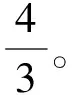
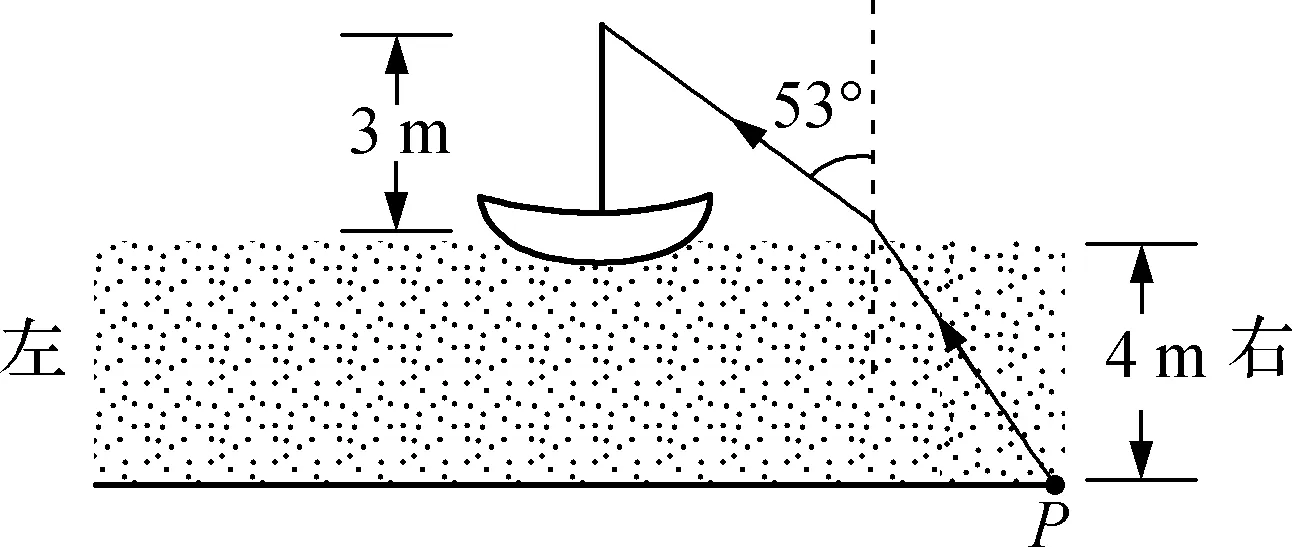
图5

(1) 求桅杆到P点的水平距离；

(2) 船向左行驶一段距离后停止,调整由P点发出的激光束方向,当其与竖直方向夹角为45°时,从水面射出后仍然照射在桅杆顶端,求船行驶的距离。

2.4.1 难点分析

光路的动态变化问题一直是几何光学的难点,帮助学生分析动态的物理过程,是使学生顺利解决临界问题的有效途径。

2.4.2 难点突破

以入射角为变量,通过折射定律求得折射角,在Geogebra中易得偏转程度与折射角大小的动态关系直线,再做出该直线与y=3的交点,就能得到随船的移动而变化的动态光路图。

2.4.3 课件制作

(1) 单击“滑动条”创建变量a,设置最小值为6,最大值为10,输入(a,0)得到点A,输入“垂线(A,x轴)”得到过点A且垂直于x轴的直线h。

(2) 输入(10,-4)得到点P,输入“线段(P,A)”,再利用“角度”工具得到直线h和线段PA间的夹角α。

(3) 依次输入α1=arcsin((4/3)*sin(α)),y=-tan(90°-α1)*x,得到直线p,再利用“平行线”工具单击点A和直线p,得到过点A且平行于p的直线i。

(4) 画出代表船的向量DC，图6展示了光随船运动的偏折过程。

图6

2.4.4 课件说明

如图6所示，滑动条角α的数值代表入射角的大小,通过滑动条改变角α,控制入射角的大小,可以直观地看到从水面射出的光线仍然照射在桅杆顶端时船移动的过程。再定量分析入射角为45°的情况,学生就能建构清晰的物理模型,正确分析对应的几何关系。

2.5 显微镜光路的探究

2.5.1 难点分析

在学生学习过透镜成像公式后,人教版高中物理选修2-3介绍了常见的光学仪器,其中显微镜和望远镜都是对透镜成像作图法和透镜成像公式的应用,而教材只给出了基本的介绍,缺少相应的定量分析。

2.5.2 难点突破

运用Geogebra建立模型,对显微镜的光路进行定量研究,可以深化学生对透镜成像作图法和透镜成像公式的理解。

2.5.3 课件制作

(1) 单击“滑动条”创建变量p,设置最小值为-10,最大值为-9,依次输入(p,0)、(p,3)得到点A、B,输入“向量“(A,B)”。

(2) 依次输入p1=1/(1/6-1/abs(p)),b=3*(p1/abs(p)),由(p1,0),(p1,b)得到点A1,B1,再利用“向量”工具得到向量A1B1。

(3) 依次输入p2=(1/(1/(30-p1)-1/16)),c=b*(p2/(30-p1)),由(-p2+30,0),(-p2+30,c)得到点A2、B2,再利用“向量”工具得到向量A2B2。

(4) 运用“直线”工具画出光路。

2.5.4 课件说明

如图7所示，滑动条p的数值代表物体到物镜的距离,通过滑动条改变p值,控制物体与物镜的距离,可以得出放大倍率和物体与物镜间距离的关系,改变物镜或目镜的焦距,还可以分析物镜与目镜的焦距与放大倍率的关系。

图7

3 结语

利用Geogebra软件制作课件，可呈现动态的物理过程。在分析物理问题时,能够帮助学生理解复杂的物理过程,在进行物理实验时,一方面可以将实验抽象成简化的物理模型,另一方面也可以用来演示一些不易做的实验,来促进学生对知识的理解。