基于模型驱动架构的电动汽车电动助力转向系统可靠性研究＊

马铮 周海鹰 李小庆 何细鹏

（1.武汉交通职业学院，武汉 430065；2.湖北汽车工业学院，十堰 442002）

主题词：电动助力转向系统 模型驱动架构 可靠性 故障树分析 电动汽车

1 前言

目前，国内外对汽车电动助力转向（Electric Power Steering，EPS）系统的可靠性研究主要集中在系统核心部件建模与控制技术、机械故障诊断两个方面。EPS系统核心部件建模技术主要指系统核心部件的数学方程描述[1]，控制技术指系统控制方法[2]、控制策略[3]；机械故障诊断方面主要包括部件的故障诊断与隔离[4]、部件优化设计及容错控制技术[5]、故障统计与预测[6]。然而，上述对EPS 系统可靠性研究的内容主要是针对该系统的单一部件，缺乏系统性研究，必须采用一种更有效的可靠性分析方法，从系统层面入手，构建EPS 系统可靠性模型并进行可靠性综合评估。文献[7]提出了基于模型的结构分析（Structural Analysis，SA）方法，该方法采用故障模式影响及危害性分析（Fault Mode Effect and Criticality Analysis，FMECA）对EPS 系统部件故障模式、故障影响进行分析，通过定性分析确定系统关键部件并建立EPS 系统故障模型，但该方法是在FMECA 定性分析下构建的系统故障模型，存在模糊不确定性且没有综合考虑软、硬件对系统可靠性的影响。陈奇等人[8-9]采用SA 方法，建立了系统故障数学模型并利用DM（Dulmage-Mendelsohn）分解和故障隔离矩阵（Fault Isolability Matrix，FIM），对系统的故障可检测性和可隔离性进行了分析，该方法侧重于故障诊断与检测能力，无法对EPS 系统整体失效率及薄弱环节进行预测评估。因此，必须从系统级模型入手，全面考虑EPS 系统各构件及其之间的依赖关系，并综合考虑软、硬件在系统运行中存在的安全问题，实现对EPS系统综合可靠性的分析。

本文将模型驱动架构（Model-Driven Architecture，MDA）[10]与故障树分析（Fault Tree Analysis，FTA）[11-12]相结合，对EPS系统可靠性进行分析评估。从系统级模型出发，综合采用结构分析与设计语言（Architecture Analysis and Design Language，AADL）[13]和错误模型附件（Error Model Annex，EMA）[14]语言，构建系统架构（EPS Architecture，A-EPS）模型及系统可靠性（EPS Reliability，R-EPS）模型，研究并改进MDA 模型到FTA模型的映射规则，实现R-EPS 模型到EPS FTA 模型的转换，最后通过FTA 定量分析预测EPS 系统失效率，定性分析确定EPS 系统可靠性关键部件并给出合理化建议，为工程实际提供理论依据。

2 A-EPS模型构建

本文提出的基于MDA的电动汽车EPS系统可靠性分析方法如图1所示。首先对EPS系统进行分析，采用AADL 对系统架构进行建模，采用EMA 对系统可靠性进行建模；其次对EPS 系统可靠性模型到故障树模型的转换进行研究，并生成故障树模型；最后通过FTA 方法对EPS 系统进行可靠性评估，并为系统改进给出合理建议。

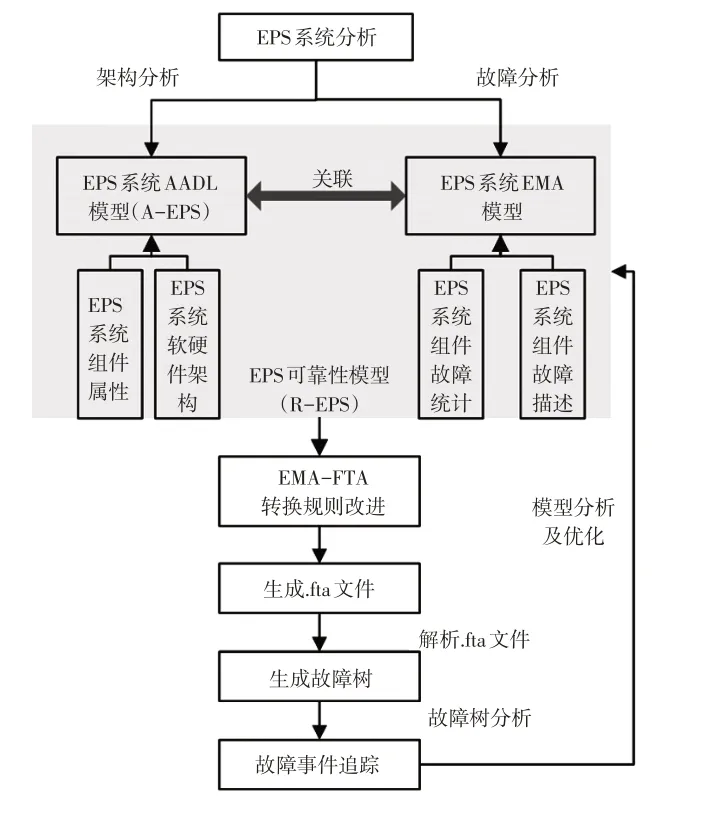
图1 基于MDA的EPS系统可靠性分析方法

2.1 EPS系统原理分析

EPS系统的结构及工作原理如图2所示。EPS系统主要由车速传感器、转向盘转矩传感器、电动机电枢电流传感器、控制器、功率驱动电路、故障指示灯、离合器和直流电动机等组成。控制器根据各传感器输出的信号决定电动机的转动方向和最佳助力扭矩，并向电动机和离合器发出控制信号，然后通过功率驱动电路控制直流电动机的转动。电动机的输出经过减速机构减速增扭后驱动齿轮齿条机构，产生相应的转向助力[15]。

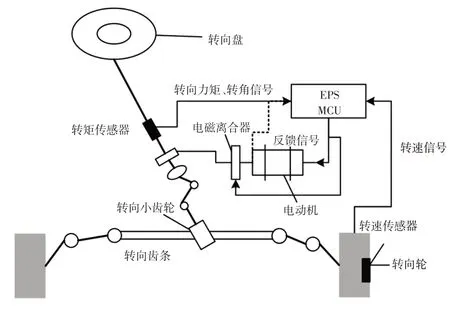
图2 EPS系统结构及工作原理

2.2 EPS系统AADL模型建立

根据EPS系统的系统组成和工作原理，其AADL模型（A-EPS模型）架构如图3所示。

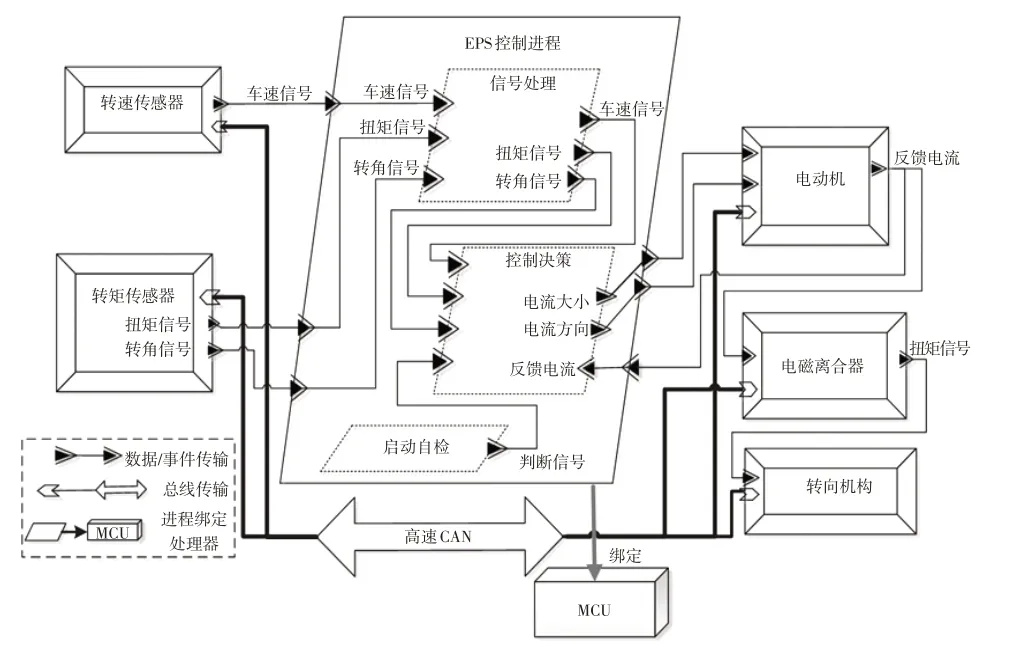
图3 EPS系统AADL模型

EPS系统由控制单元、轮速传感器、扭矩传感器、电动机、电磁离合器以及转向机构组成。控制单元包含信号处理、决策控制和启动自检3个线程。控制单元绑定于微控制单元（Microcontroller Unit，MCU），各传感器、电动机、电磁离合器、转向机构之间通过CAN 总线相连。

考虑试验样车的部分软件参数，使用标准属性集和自定义属性集对输入/输出（I/O）端口、任务类型、总线属性、处理器相关属性等进行详细描述。其中控制决策线程具有周期性且周期为30 ms，计算截止时间默认等于周期，计算执行时间为3 ms。处理器采用NXP STM32L431RCT6，线程交换执行时间为2～3 ns，调度策略采用最早截止期限优先（Earliest Deadline First，EDF）策略，采用高速CAN 总线和载波侦听多路访问（Carrier Sense Multiple Access，CSMA）协议，硬件部分采用VHSIC 硬件描述语言（Very-High-Speed Integrated Circuit Hardware Description Language，VHDL）。此外，还可以对线程的优先级、调度策略，以及处理器的处理速率、优先级范围和总线的带宽等进行详细设置。

3.R-EPS模型构建与转换

3.1 EPS系统故障统计分析

本文故障数据来源于某自主品牌电动汽车在开发测试期间内240 辆样车一年内重复试验的全部故障跟踪记录[16]。通过对故障数据进行统计分析，全部样车中主要故障部位共有10处，分布情况如表1所示。

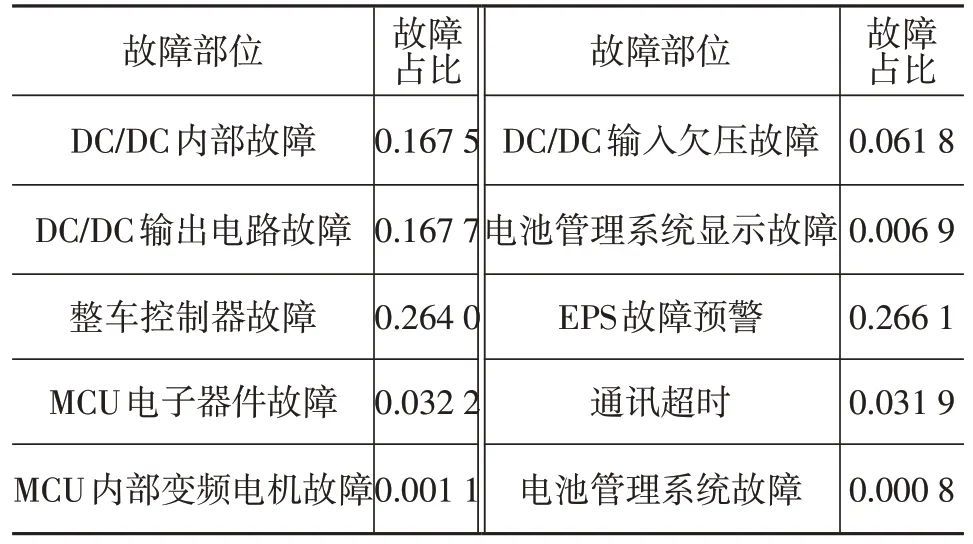
表1 故障部位统计

由表1 可知，EPS 故障预警占故障总数的26.6%。对EPS 系统的结构及工作原理进行分析，该系统的故障主要分为硬件故障、软件故障、电路故障，其中硬件故障主要是EPS 控制器（MCU）、电磁离合器、电动机、转矩传感器、车速传感器等部件故障，软件故障主要是车速、转角、转矩、反馈电流等信号处理失效，电路故障主要是部分器件电路的短路、断路以及触点的异常连接。

文献[17]推导出了EPS 系统常见元器件的失效特征参数。本文在其基础上，结合实际故障统计数据分析得出常见EPS 故障底事件及其失效概率，如表2所示。

3.2 EPS系统EMA模型构建

AADL可靠性模型由AADL架构模型（A-EPS模型）和AADL 错误模型附件（EMA）两部分构成[13]。EMA 描述了组件可靠性相关的信息，包括故障类型、故障事件、故障状态、故障状态变迁、故障分布等。

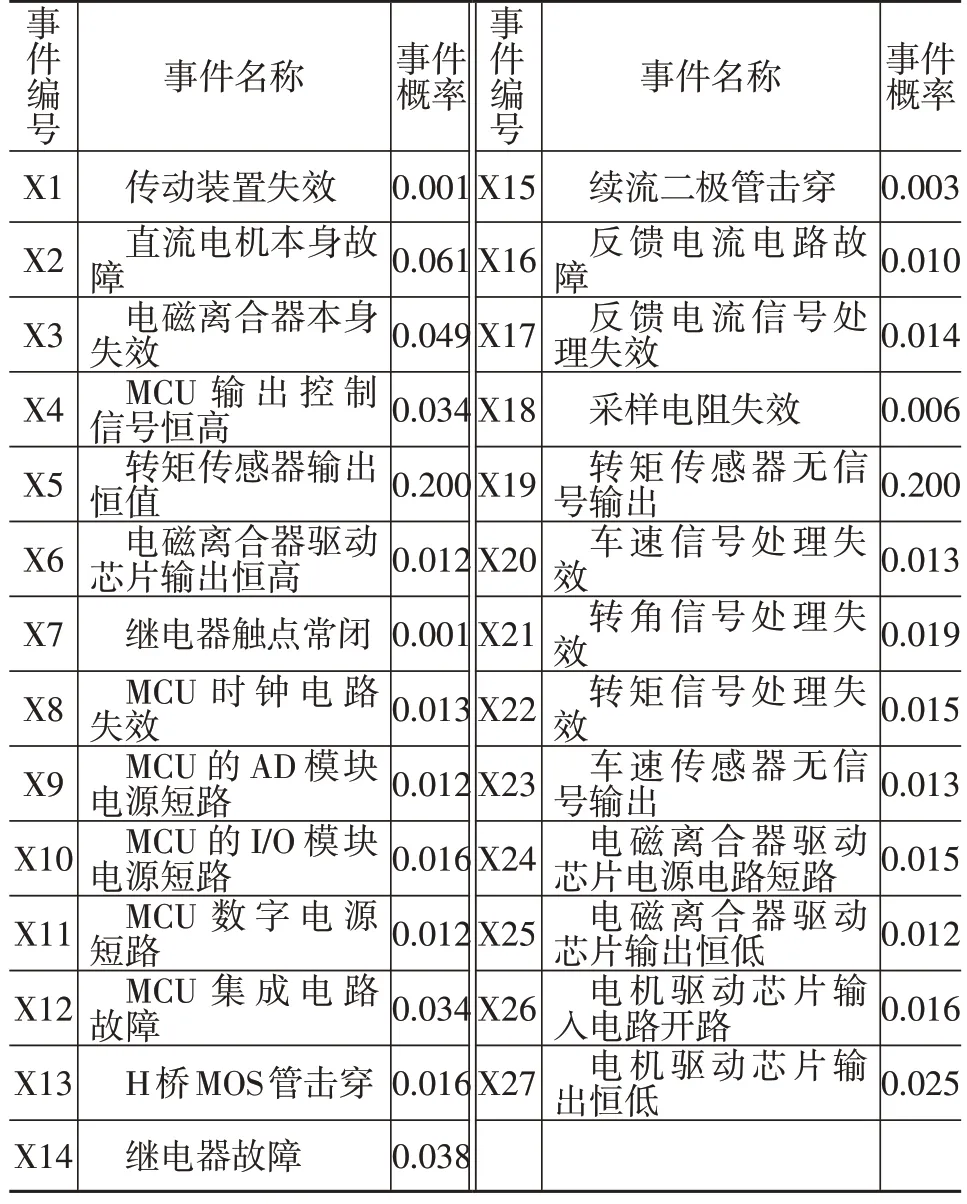
表2 EPS故障底事件

为构建EPS 系统EMA 模型，需要对各元件的故障信息进行描述，本文利用EMA 语言构建了子系统通用错误模型：

标记（1）定义了故障类型，可以采用EMA标准集中提供的，也可以自定义故障类型，例如信号处理故障，标记（2）定义了故障事件及故障状态（operational 和failed），标记（3）定义了故障变迁，标记（4）定义了故障分布类型，可分为泊松（Poisson）和固定（Fixed）概率分布，此外还可定义严重性级别、可能性、危害性等。标记（2）～标记（4）共同定义了故障行为模型。

将AADL 架构模型和AADL 错误模型相结合即可构建EPS系统可靠性模型，其中EPS系统进程控制的可靠性模型为：

从模型中可以看出，当进程EPS_control 中线程signal_ processing、startup、control_decision 均失效时，进程EPS_control 失效。其中部分故障数据，例如故障分布、失效概率由测试数据分析得出，其他数据由可靠性预计模型及失效参数推导得出。

3.3 EMA模型到FTA模型的转换规则

文献[18]、文献[19]描述了从AADL 模型到静态故障树的转换方法，但这些方法中缺乏对构件间干扰性的考虑，没能对故障构件间的相关性进行描述。李东民等人[20]描述了从AADL 故障模型到动态故障树的转换方法，但该模型中缺少对底事件故障分布及故障产生概率的描述。因此，本文在前者研究基础上，对EMA模型到FTA模型转换规则进行了改进：

定义1：基本故障树可以定义为一个四元组F=(T,I,B,G)。其中：T为顶事件（Top Event），位于故障树顶端，表示所有事件联合发生作用的结果；I为中间事件（Intermediate Event）集合，位于顶事件和底事件之间；B为底事件（Bottom Event）集合，包括基本事件（Basic Event），表示该事件已无需继续探明原因，且故障模式已知；G表示门（Gate）集合，包括或门（Or Gate）和与门（And Gate）。

定义2：EMA 的基本元素可表示为一个四元组E=(ES,EE,T,O)。其中：ES={es1,es2,…,esm}为所有错误状态的集合；EE={ee1,ee2,…,eem}为所有错误事件的集合；O为错误事件的故障分布及发生概率的集合；T为所有错误状态间变迁的集合，转移函数T(esi,eej)=esk。

对比EMA 及FTA 模型基本元素，可得到这2 种模型中元素的对应关系，转换规则如下：

规则1：错误模型中的错误事件转换为故障树中的底事件。

规则2：错误模型中的错误事件概率转换为故障树底事件概率。

规则3：错误模型中的错误状态转换为故障树中的中间事件或顶事件。

规则4：错误模型的连接弧转换为故障树中的逻辑门，其中逻辑门的转换规则有2种：

a.EMA 中的复合错误行为（Composite Error Behavior）描述的是复合故障行为，表述错误事件与状态变迁之间的关系。与（And）表示几个错误事件均发生才导致状态变迁，或（Or）表示任意一个事件发生都将导致状态变迁。因此，可将EMA 中的And 转换为FTA 的与门，EMA中的Or转换为FTA的或门。

b.不同故障事件间的相关性：当eei与eej之间存在相关性，即故障事件i发生会引发故障事件j发生，则可转换为与门；若eei与eej间不存在相关性，即故障事件i发生不会引发故障事件j发生，则可转换为或门。

3.4 R-EPS系统FTA模型的生成

在构建好EPS系统可靠性模型（R-EPS模型）后，将其进行实例化，包含EPS 系统架构实例和错误模型实例，基于3.3节模型转换规则将这些错误模型实例进行转化，并通过软件OSATE的故障树分析运行（Run Fault Tree Analysis）插件生成.fta 文件，最后通过OpenFTA 工具解析.fta 文件，生成EPS 故障树模型。图4 所示为最终生成的EPS系统FTA模型，其中各中间事件名称及编号如表3所示。

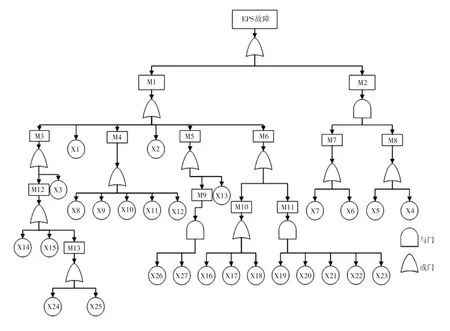
图4 EPS系统FTA模型

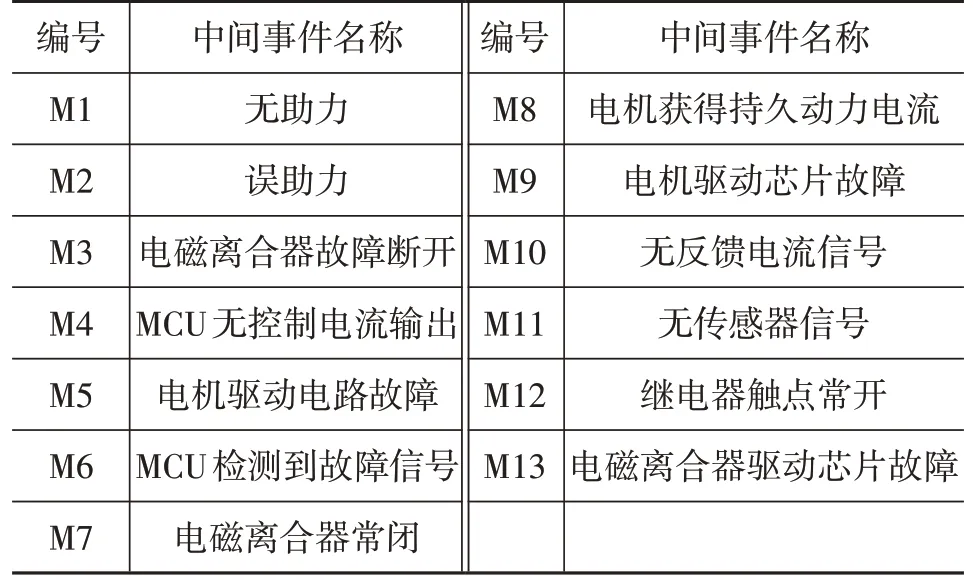
表3 中间事件编号及名称

4 R-EPS系统可靠性分析

4.1 R-EPS系统FTA定量分析

设X={X1,X2,…,Xn}为故障树的n个互相独立的底事件的集合，故障树的结构函数表示为：

式中，n为故障树所有底事件的数量；xi为相应底事件是否发生的状态。

与门和或门的结构函数分别为：

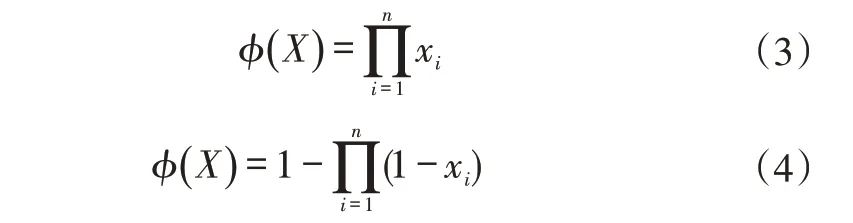
依据逻辑门的概率计算公式[19]，可分别求得与门和或门下系统的不可靠度Fs(t)：

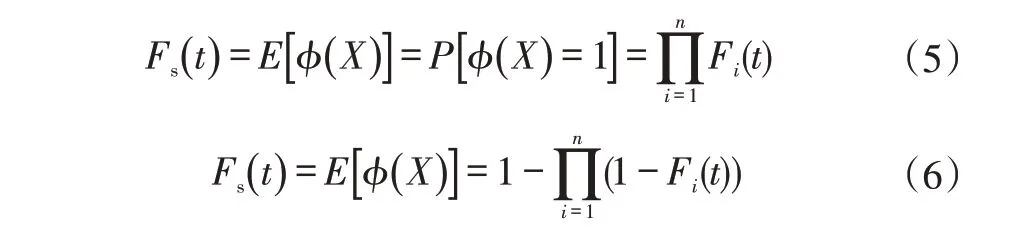
依据EPS系统FTA模型以及表1中EPS故障底事件及其概率，可逐层求出各中间事件的概率，最终求得顶上事件概率。经计算，顶上事件概率为0.274，对比3.1节故障统计数据，EPS故障预警占故障总数的26.6%，实际测试与模型分析数据误差为3%，准确度较高。

4.2 R-EPS系统FTA定性分析

根据故障树底事件或最小割集对顶事件产生的贡献，可以确定系统薄弱环节并以此改进系统方案设计，可分为概率重要度、临界重要度和结构重要度[21]。

4.2.1 基本事件概率重要度分析

基本事件概率重要度表述第i个元件不可靠度的变化导致系统不可靠度变化的程度。g函数为顶上事件发生概率，其为多重线性函数。对自变量Fi(t)求偏导即可得到基本事件的概率重要度Igi：

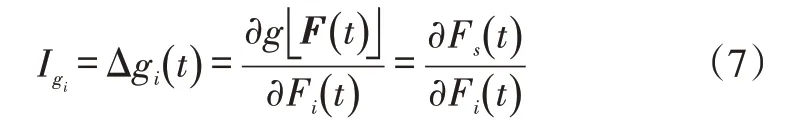
式中，为顶事件发生概率；

利用式（7）可求出各基本事件的概率重要度，排序结果如表4所示。

从表4中可以看出，事件继电器触点常闭（X7）造成的影响最大，转矩传感器输出恒值（X5）、电磁离合器本身失效（X3）造成的影响次之，因此系统工程师在设计时应多注重这些关键部件，尽可能降低其故障概率，必要时设计容错系统，以提高整个系统的可靠性。影响最小的是事件为X19～X23，多为软件类型故障。

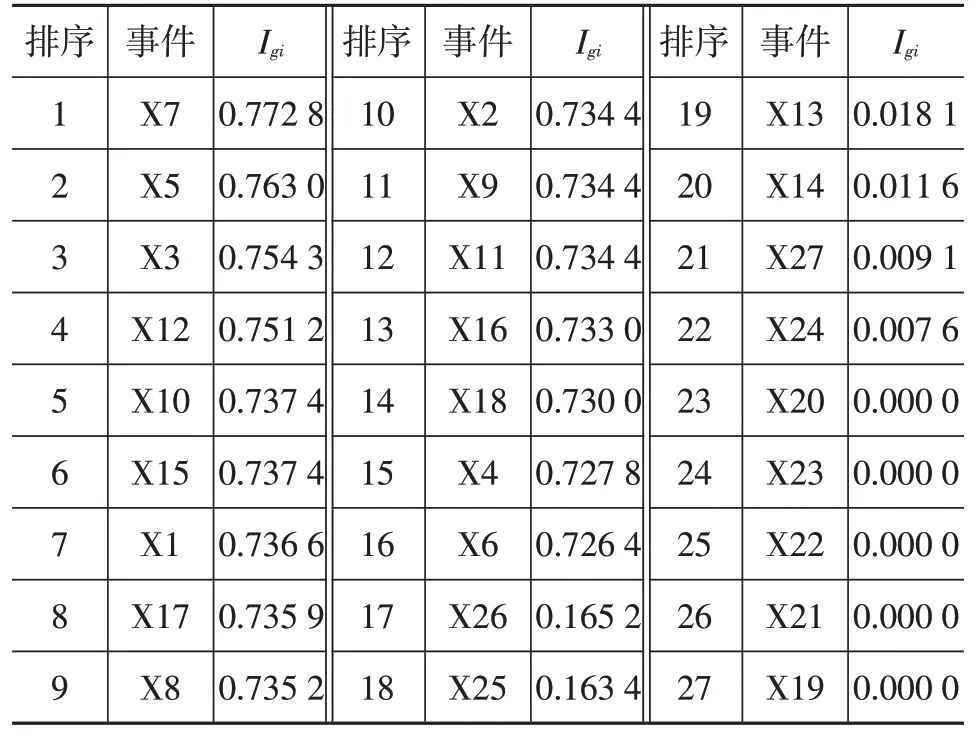
表4 基本事件概率重要度

4.2.2 临界重要度分析

临界重要度也称关键重要度，是从系统安全角度考虑，用基本事件发生概率的相对变化率与顶上事件发生概率的相对变化率之比来表示基本事件的重要度[21]，它是综合考虑敏感度和自身发生概率来衡量各基本事件的重要度标准：

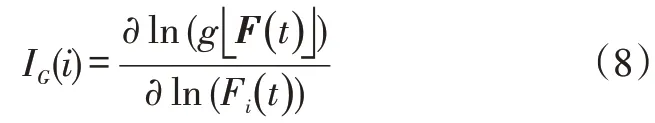
概率重要度和临界重要度IG(i)的关系为：

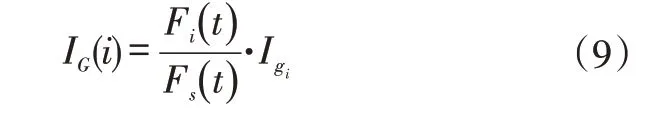
根据式（8）、式（9）可得出各基本事件临界重要度，如表5所示。

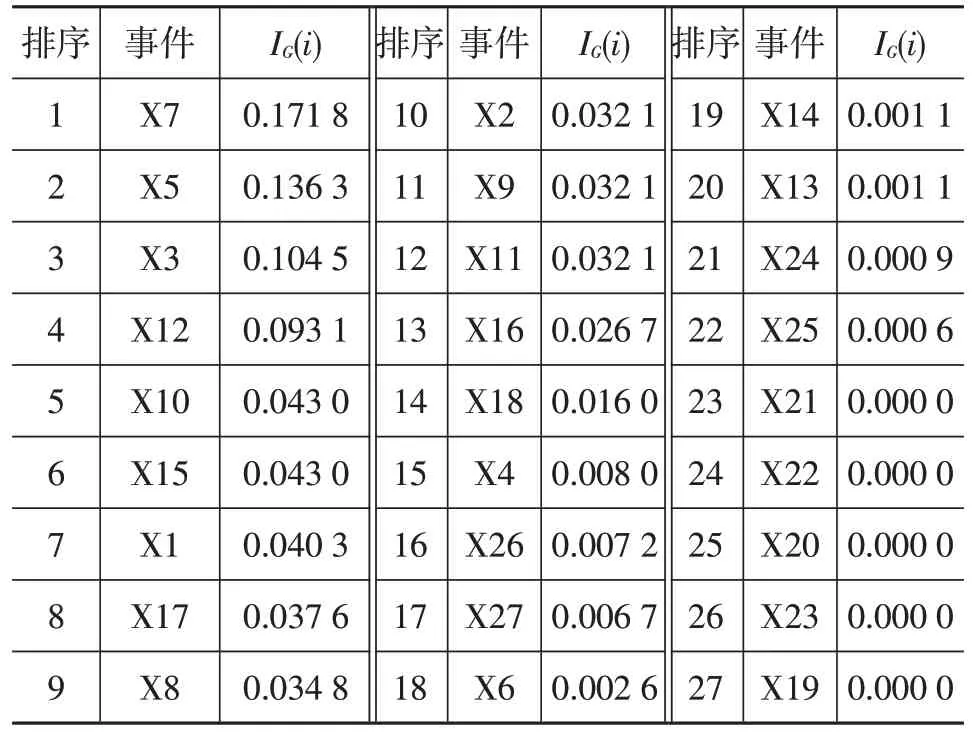
表5 基本事件临界重要度

由表5可知，临界重要度最高的3个事件分别为继电器触点常闭（X7）、转矩传感器输出恒值（X5）、电磁离合器本身失效（X3），与基本事件概率重要度结果分析相近。

4.2.3 结构重要度分析

结构重要度表述元部件在所处系统中的重要程度，与该系统的元部件自身故障概率并无关系，仅从结构上分析各基本事件对顶上事件发生的影响程度，其数学表达式为：

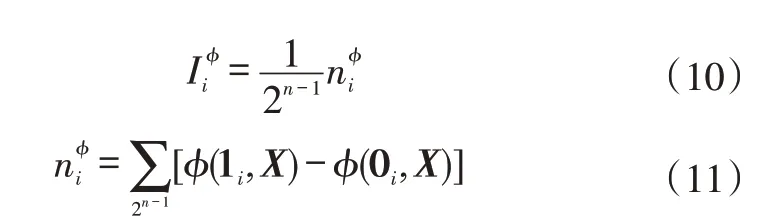
经分析得出EPS系统结构重要度为I(X18)=I(X17)=I(X16)=I(X15)=I(X11)=I(X10)=I(X9)=I(X8)=I(X7)=I(X6)=I(X5)=I(X4)=I(X3)=I(X2)=I(X1)＞I(X27)=I(X26)=I(X25)=I(X24)=I(X14)=I(X13)＞I(X23)=I(X22)=I(X21)=I(X20)=I(X19)。这表示采样电阻失效、反馈电流信号处理失效、反馈电流电路故障等事件在EPS 结构上具有最高的重要程度，处于系统关键部位，其次为电机驱动芯片输出恒低、电机驱动芯片输入电路开路等，最后为转角信号处理失效、转矩信号处理失效等。

5 结束语

本文提出了基于MDA的电动汽车EPS系统可靠性评估方法。依据某自主品牌电动汽车开发测试期间故障跟踪记录，以及部分元器件的失效特征参数分析得出EPS 系统常见故障事件及失效概率。利用AADL 建立了系统架构模型（A-EPS 模型），在此基础上利用EMA子语言建立了系统可靠性模型（R-EPS 模型），并对EMA 模型到FTA 模型的转换规则进行了改进，生成了系统FTA 模型，最后通过FTA 定量、定性分析得到以下结论：系统分析误差为3%，准确度较高；导致EPS 失效的重要事件为继电器触点常闭、转矩传感器输出恒值、电磁离合器本身失效，影响最小的事件多属于软件类型故障；采样电阻失效、反馈电流信号处理失效、反馈电流电路故障等事件重要程度最高，处于系统关键部位，其次为电机驱动芯片输出恒低、电机驱动芯片输入电路开路等，最后为转角信号处理失效、转矩信号处理失效等。

该方法体系可在系统开发前期对系统薄弱环节进行排查，为系统的改进及元件健康管理提供理论依据。