CL⁃20/1,4⁃DNI共晶及共晶组分的声子谱和热力学性质的第一性原理研究
郭 蓉,段晓惠,李洪珍,伍 波
(1.西南科技大学环境友好能源材料国家重点实验室,四川 绵阳621010;2.中国工程物理研究院化工材料研究所,四川 绵阳621999)
1 引言
在制造、运输、存贮和使用中,开展含能材料初始引爆机理的研究具有十分重要的理论和实际意义[1]。目前实验上主要通过监测升温或升压过程中的热分解产物来逆向反推热分解机理[2-3],而理论模拟则主要通过分子动力学(MD)方法来直观模拟升温或升压时的分解过程[4-5]。但这些方法均不能解释外界刺激如何转移到原子或基团上、能量在含能材料中的分布及传导过程。对驱动含能材料引发化学反应的潜在机制尚不清晰。声子是晶格振动的元激发,其作为热载体在克服能垒和引发热分解反应中起着重要作用[6-9]。Dlott 和Fayer[10]提出了一种“多声子向上泵浦”模型来研究冲击诱导下凝聚相有机含能化合物的热能流动情况:当冲击波开始在有机含能晶体中传播时,过剩的机械能和热能首先作用于晶格振动模式产生热声子,热声子进而与低频振动区(即“入口模”区)发生非谐耦合作用,将能量传递到高频振动区,进而引发化学键的断裂。
声子谱显示了声子能量与动量的关系,是研究固体热力学性质(热容和热膨胀等)和微观过程(热传导)的 重 要 手 段[11-15]。Long Yao[16]等 开 发 了 一 种 计 算HMX 声子态密度的物理模型,据此推导出了HMX 的状态方程、热膨胀系数、体积模量、恒压比热和Hugo‑niot 曲线等热力学性质,理论计算结果与低压实验数据相吻合。Kraczek 等[17]运用MD 方法计算了α‑RDX的声子谱,由于晶格声子的贡献显著大于热弛豫阶段内部声子的贡献,判断是通过晶格振动传热并引起键断裂。
综上,声子谱的研究可以从微观层次加深对含能材料冲击诱导引爆过程的理解。目前文献报道主要集中在单质炸药,而对共晶炸药声子谱及热力学性质的研究则较少[18]。CL‑20/1,4‑DNI共晶具有较高的晶体密度(1.922 g·cm-3)和优异的热稳定性。其爆轰性能(爆速9242 m·s-1,爆压39.01 GPa)低于CL‑20(9792 m·s-1,45.07 GPa),但 明 显 高 于1,4‑DNI(8270 m·s-1,29.65 GPa),与目前综合性能最优的高能炸药HMX(9214 m·s-1,38.58 GPa)相当,但撞击感度(10 J)明显优于CL‑20(2.5 J)和HMX(6 J),高能低感的特性使其可能在高效毁伤钝感弹药中得到应用[19]。因此,本研究以CL‑20/1,4‑DNI 共晶为研究对象,采用第一性原理方法,研究共晶及共晶组分的声子谱和热力学性质,揭示其爆轰性能和感度的微观物理机制,为化学分解前的能量传递过程提供重要信息。
2 计算方法
2.1 模型构建及结构优化
基于剑桥晶体数据库(CCDC)构建CL‑20/1,4‑DNI[19]、1,4‑DNI[19]和ε‑CL‑20[20]的单胞结构,如图1 所 示。CL‑20/1,4‑DNI 共 晶 中 共 有8 个 分 子,CL‑20 和1,4‑DNI 各4 个,为1∶1 型 共 晶。其 中,CL‑20 分 子 的 构 象 与ε‑CL‑20 晶 体 中 的 构 象 相 同。CL‑20/1,4‑DNI 共 晶 为 正 交 晶 系,空 间 群 为P212121,与1,4‑DNI 相 同,显 著 不 同 于ε‑CL‑20(单 斜 晶 系,P21/n)。
利用Materials Studio 材料模拟平台中的CASTEP模块分别对CL‑20/1,4‑DNI、1,4‑DNI 和ε‑CL‑20 晶体进行结构优化。在周期性边界条件内,电子的交换相关函数选用广义梯度近似(generalized gradient approxi‑mation,GGA)和PBE(Perdew‑Burke‑Ernzerhof)方法。由模守恒赝势(norm‑conserving Pseudopotential)代替离子实,平面波基组描述体系的电子波函数,并引入TS 色散校正法修正范德华力的计算。截止能量选为830 eV,k点1×2×2,电子弛豫标准≤1×10-6eV/atom。
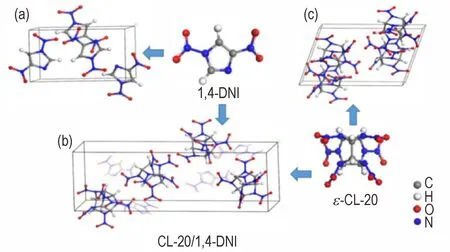
图1 1,4‑DNI[19],CL‑20/1,4‑DNI[19]和ε‑CL‑20[20]的晶胞结构及分子结构Fig.1 The unit cell structures of 1,4‑DNI[19](a),CL‑20/1,4‑DNI[19](b)and ε‑CL‑20[20](c)and their molecular struc‑tures
2.2 声子谱计算
基于优化后的晶体结构,采用有限位移法计算单点能,通过分析得到声子色散曲线和声子态密度。模拟参数设置:q 矢量间距为0.015 Å-1,声子色散精度0.015 Å-1,声子态密度为2×2×3。
3 结果与讨论
3.1 优化后的结构
表1 列出了CL‑20/1,4‑DNI 共晶和共晶组分优化后的晶胞参数及与实验值的相对误差。从表1 中可看出,计算值和实验值的相对误差均<3%,在计算声子谱的允许误差范围之内,同时也说明计算方法和参数设置的可靠性。

表1 CL‑20/1,4‑DNI、1,4‑DNI 和ε‑CL‑20 晶体的晶胞参数和相对误差Table 1 Cell parameters and relative errors of CL‑20/1,4‑DNI,1,4‑DNI and ε‑CL‑20 crystals
3.2 声子色散曲线
CL‑20/1,4‑DNI 共晶及共晶组分声子色散曲线的计算结果如图2 所示。CL‑20/1,4‑DNI 晶胞中包含8个分子(196 个原子)[19]和588 条色散曲线,1,4‑DNI晶胞内含4 个分子(52 个原子)[19]和156 条色散曲线,ε‑CL‑20 晶 胞 中有4 个分子(144 个原子)[20]和432 条色散曲线。在布里渊区中心点(即倒格子原胞的原点)附近均没有虚频,表明结构优化的参数设置合理,优化后 的 结 构 稳 定。此 外,CL‑20/1,4‑DNI、1,4‑DNI 和ε‑CL‑20 存 在 较 大 带 隙,带 隙 宽 度 分 别 为43.29,46.17 THz 和44.13 THz。可见,形成共晶后带隙宽度变窄,这种现象在其它共晶中也有发现[21]。
根 据“ 多 声 子 向 上 泵 浦”理 论[10],将CL‑20/1,4‑DNI 共晶及共晶组分的声子态密度划分为五个频段。其中,选择ωc作为第一条带隙处的振动频率,小于ωc为外振动区(又称晶格振动区),ωc~2ωc为“入口模”区,而内振动A、B 和C 区由声子色散谱中明显的带隙来确定,详细划分结果见表2。采用直接计数法计算了ε‑CL‑20,CL‑20/1,4‑DNI 和1,4‑DNI 的“入口模”声子数,分别为44、26 和13。有研究表明“入口模”声子数与撞击感度呈线性正相关,即入口模数越大,撞击感度越高[14,22]。因此,根据“入口模”声子数预测的撞击 感 度 顺 序 为ε‑CL‑20> CL‑20/1,4‑DNI>1,4‑DNI。此外,按照文献[23]定义特征振动频率Δωd(=ωd‑ωc),其值也可用于撞击感度相对高低的预测,即ωc与“入口模”区第一条频率(ωd)之间的带隙越大,撞击感度越低。ε‑CL‑20,CL‑20/1,4‑DNI 和1,4‑DNI 晶体的Δωd分别为4.858,15.203 cm-1和46.919 cm-1,由此预测的撞击感度顺序为:ε‑CL‑20> CL‑20/1,4‑DNI>1,4‑DNI。实 验 上 对 撞 击 感 度 的 测 试 结 果 为ε‑CL‑20∶IS=2.5 J,CL‑20/1,4‑DNI∶IS=10 J 和1,4‑DNI∶IS=14 J[19]。可见两种方法预测的撞击感度顺序与实验结果相一致。

图2 CL‑20/1,4‑DNI、1,4‑DNI 和ε⁃CL‑20 晶体的计算声子色散曲线Fig.2 Phonon dispersion curves of CL‑20/1,4‑DNI,1,4‑DNI and ε⁃CL‑20 crystals obtained by caculation

表2 CL‑20/1,4‑DNI、1,4‑DNI 和ε‑CL‑20 晶体的振动模式划分Table 2 Division of vibration modes of CL‑20/1,4‑DNI,1,4‑DNI and ε‑CL‑20 crystals THz
3.3 ε⁃CL⁃20 晶体的声子态密度
ε‑CL‑20 的 声 子 态 密 度 如 图3 所 示,图3a 为 总 态密度,图3b 和图3c 分别为选定基团和原子的态密度。表3 为选定基团对声子态密度的贡献。从表3 可以看出,ε‑CL‑20 晶体中,O─N─O 基团对晶格振动区的贡献最大,为87.01%,而其它基团的声子态密度较小。因此,根据“多声子向上泵浦”原理[10]可以认为,O─N─O 基团对于外加刺激的应激反应将最明显。其次,在表示能量进入或离开分子的“入口模”区,O─N─O 基团的贡献仍最大(58.45%),且N─N 和笼形骨架(Skeleton)的百分比均大于40%,而碳原子在“入口模”区的声子态密度非常弱,最大值小于0.006 THz-1(图3c),因此“入口模”区主要由N─NO2决定。从晶格振动区到“入口模”区,O─N─O 的贡献从87.01%减少到58.45%,而N ─N 和Skeleton 的增幅均大于23%(表3)。这表明能量从O─N─O 流经N─N键并进一步转移到Skeleton 上的其它原子,多余的能量将通过分子内振动再分布(IVR)过程进一步消散。因此,可推测ε‑CL‑20 晶体中分子引发键是N─NO2。在易引起化学键断裂的30~60 THz 中,即内振动区,选定基团的占比均大于30%,也就是说在IVR过程中,化学键可能会被激发并最终断裂。已有实验和理论模拟发现,不同晶型CL‑20 的分解均始于N─NO2键的断(均)裂,进而是C─N 和N─N 键断裂发生开环反应[24-25],本研究从晶格振动和能量转移角度印证了这一观点。此外,声子频率的高低与原子质量有关,轻原子在高频区的振动明显。因此随着频率的增加,C─H 键的振动具有明显增强的趋势。在内振动C 区,氢原子的振动占主导地位。
通过以上声子态密度的分析,可得到ε‑CL‑20 晶体的能量流动方向,如图3a 所示。外界刺激后过剩的热能和机械能首先转移到O─N─O 基团上发生振动弛豫,产生热声子。热声子与相邻原子发生非谐耦合,促使能量从O─N─O 基团流到N─N 键,最后流至Skeleton 上的其它原子。

图3 ε⁃CL‑20 晶体的声子态密度Fig.3 Phonon density of states of ε‑CL‑20 crystal
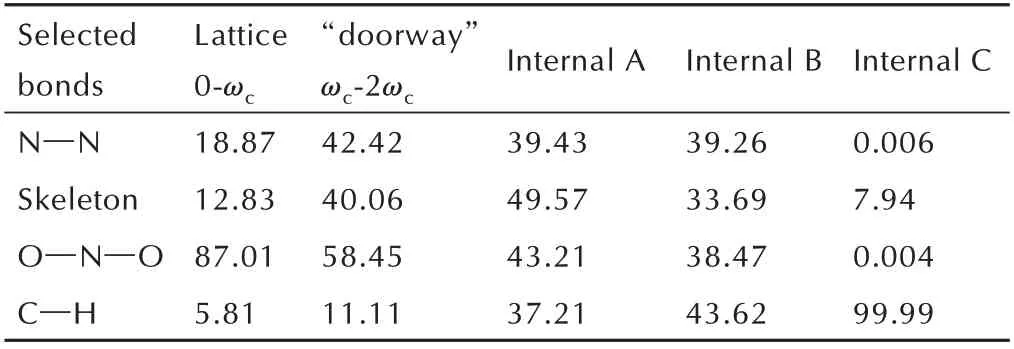
表3 ε‑CL‑20 晶体中选定基团对声子态密度的贡献Table 3 Contribution of each selected bond to phonon den‑sity of states in ε‑CL‑20 crystals %
3.4 1,4⁃DNI 晶体的声子态密度
图4 是1,4‑DNI 晶体的声子态密度,图4a 为总态密度,图4b 和图4c 分别为选定基团和原子的态密度。表4 为选定基团对声子态密度的贡献。从图4a 可以看出,振动频率范围主要在0~48.07 THz 和94.14~96.65 THz,而在48.07~94.14 THz 频段内的声子态密度为零。图4b 和表4 显示,在0~5.82 THz 的晶格振动区,O ─N ─O 基团对晶格振动的贡献最大(67.19%),其 次 是 咪 唑 环 骨 架(Skeleton),为30.69%,表明当有外界刺激时,O─N─O 的晶格热振动最强烈。此外,Skeleton 对外加刺激的应激反应也较明显。在“入口模”区,O─N─O 和Skeleton 的模式振动位居第一和第二。从晶格振动区到“入口模”区,O ─N ─O 和C ─H 的 贡 献 分 别 降 低 了11.53% 和2.7%,而其它基团均有不同程度的增加,其中C─NO2和N ─NO2共 增 加 了14.26%,Skeleton 增 加 了10.64%。图4c 显示氢原子在低频区的振动非常弱。

图4 1,4‑DNI 晶体的声子态密度。Fig.4 Phonon density of states of 1,4‑DNI crystal

表4 1,4‑DNI 晶体中选定基团对声子态密度的贡献Table 4 Contribution of each selected bond to phonon den‑sity of states in 1,4‑DNI crystal %
综上,1,4‑DNI 晶体中能量流动的总趋势是从O─N─O 经C─N 和N─N 键流入咪唑环内。在容易引起化学键断裂的高频段(30~60 THz)内,咪唑环的晶格热振动最剧烈,据此推测1,4‑DNI 的初始热分解更易发生咪唑环的开环反应。由于对1,4‑DNI 的初始热分解机理目前尚未见文献报道,仅刘慧君[26]等报道了1,4‑DNI 热重排制备2,4‑DNI 的研究工作,因此该推测还需进一步证实。
3.5 CL⁃20/1,4⁃DNI 共晶的声子态密度
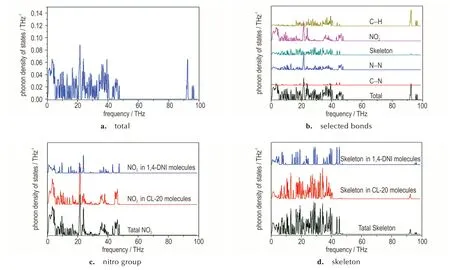
图5 CL‑20/1,4‑DNI 共晶的声子态密度Fig.5 Phonon density of states of CL‑20/1,4‑DNI cocrystal
图5 为CL‑20/1,4‑DNI 共 晶 的 声 子 态 密 度,表5为选定基团对声子态密度的贡献。由图5b 和5c 可以看出,在晶格振动区和“入口模”区,O─N─O 基团在总声子能量中占比最大,特别是CL‑20 分子中的O─N─O 贡献最大。因此,CL‑20 分子中O─N─O的晶格热振动为“热声子”的产生起到重要作用。同样地,从晶格振动区到“入口模”区,可以观察到O ─N ─O 的百分比减小,其它基团均有不同程度的增大(见表5),而N─N 和环骨架(Skeleton)的增幅 最 大,能 量 流 动 方 向 是 从O ─N ─O 经N ─N 键流到环骨架中的其它原子。此外,共晶中1,4‑DNI分 子 的C ─N 基 团 仅 增 加 了0.97%,比1,4‑DNI 单体的C─N 基团(7.43%)少很多,说明形成共晶后,1,4‑DNI 分子的晶格热振动受到抑制。在引起化学键 断 裂 的30~60 THz 频 段,以O ─N ─O 和 环 骨 架为例,CL‑20/1,4‑DNI 共晶中CL‑20 分子比1,4‑DNI分子的声子数更多,声子态密度峰更强(见图5c 和图5d)。因 此,在CL‑20/1,4‑DNI 共 晶 中,CL‑20 分子的晶格热振动占主导地位,即CL‑20 分子不仅吸收更多的能量,对外部刺激的应激反应也更强,更易发生化学键的断裂。 因此,可推测CL‑20/1,4‑DNI 共 晶 的 初 始 热 分 解 始 于CL‑20 分 子 的N─NO2键。

表5 CL‑20/1,4‑DNI 共晶中选定基团对声子态密度的贡献Table 5 Contribution of each selected bond to phonon den‑sity of states in CL‑20/1,4‑DNI cocrystal %
图6 绘制了一个CL‑20 分子和一个1,4‑DNI 分子分别在CL‑20/1,4‑DNI 共晶及 纯组分中的声子态密度。从图6a 可以直观地看出,共晶中CL‑20 分子的峰比在ε‑CL‑20 晶体中的弱,但峰位和峰形基本相同。同样地,1,4‑DNI 分子也表现出了相同的规律(见图6b),但峰强降低得更为明显。基于力参数矩阵与近邻原子间相互作用关系[26],可知声子谱能够从本质上反映出近邻原子间的相互作用。因此,这些差异可归因为形成共晶后分子构象和分子间相互作用的变化。图6 中声子态密度的对比说明:(1)CL‑20 和1,4‑DNI形成共晶后没有发生分子构象的转变,这与单晶结构测试结果相一致[19‑20];(2)CL‑20/1,4‑DNI 共晶中存在NO2‑π、CH…O 和CH…N 等相互作用。这些相互作用导致CL‑20 分子和1,4‑DNI 分子的晶格热振动受到抑制,热稳定性得到改善,从而使共晶的热稳定性优于两个单体,与实验差示扫描量热法测试结果相吻合[19]。
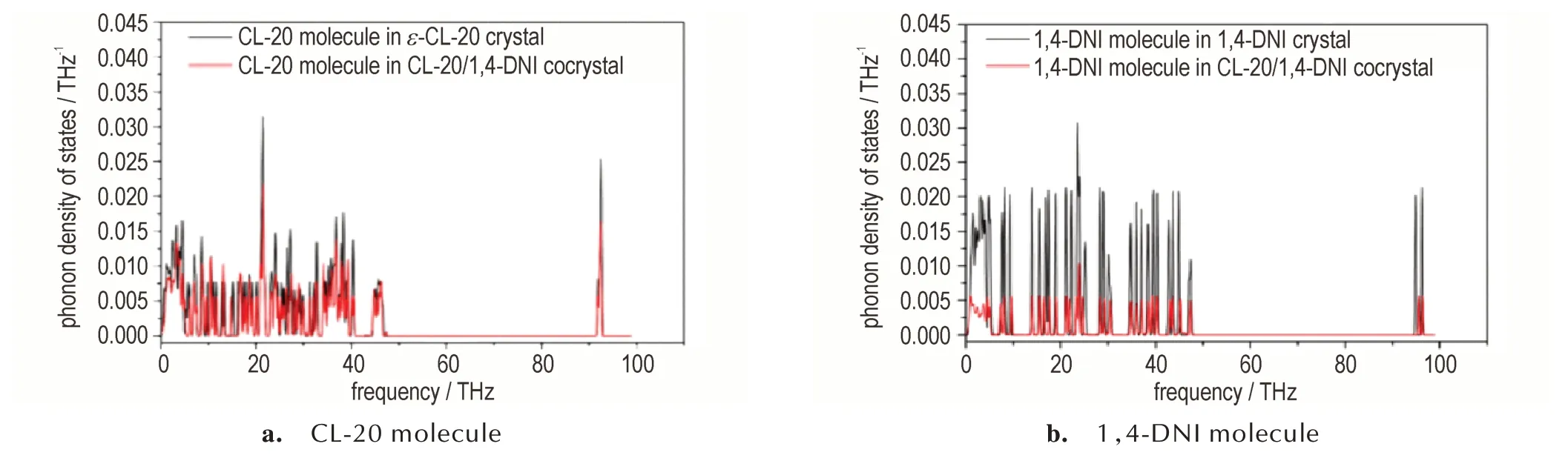
图6 CL‑20 和1,4‑DNI 分子分别在共晶和纯组分中的声子态密度Fig.6 Phonon density of states of CL‑20 and 1,4‑DNI molecules in cocrystal and pure components,respectively
3.6 热力学性质分析
材料的热力学性质与晶格振动密切相关,利用晶格振动频率计算材料的热力学性质关系如下[27]:
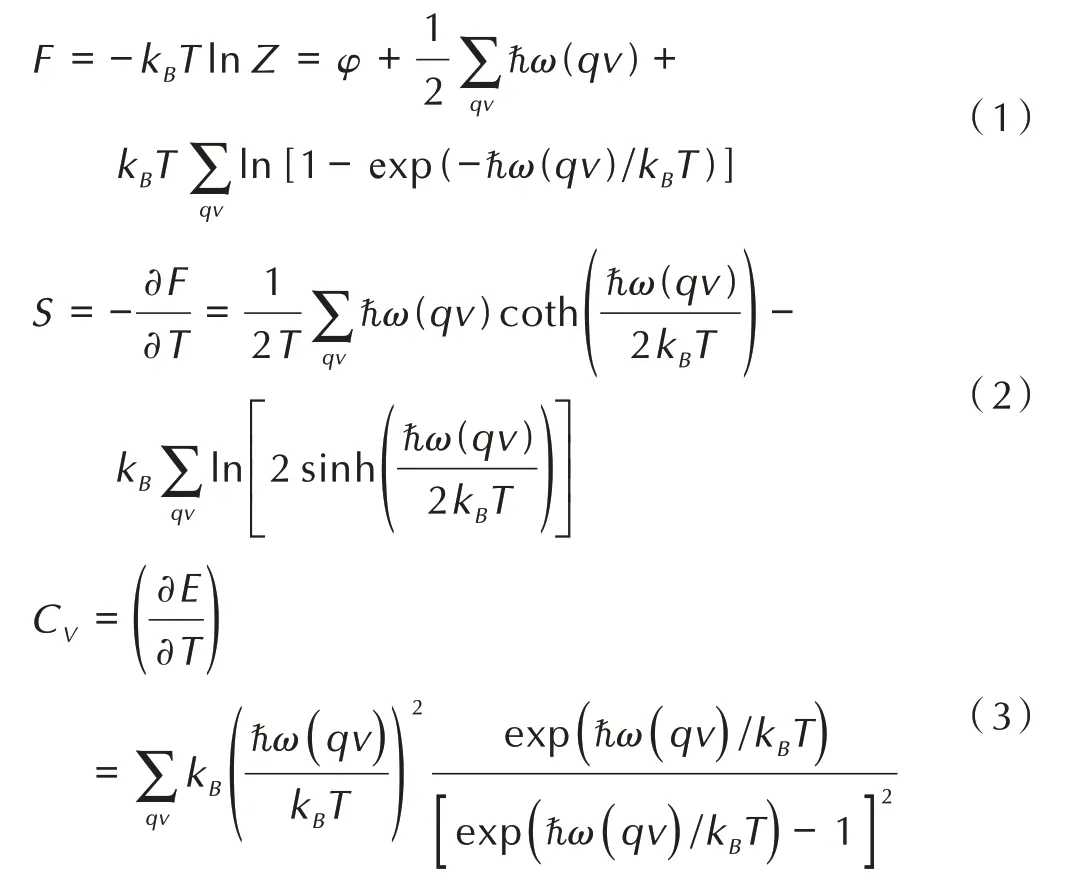
式中,F为赫姆霍兹自由能,eV;S为熵,eV·K-1;CV为恒容热容,J·mol-1·K-1;波矢q,rad·m-1;和角频率ω,rad·s-1。
图7 显示了温度对CL‑20/1,4‑DNI 共晶及共晶组分热力学参数的影响趋势。其中,图7a 为TS 随温度的变化关系。温度增加,共晶及共晶组分中原子的热运动加剧,粒子的无序度增加,导致S 随温度的增加而增加。此外,由于晶体内共价键的作用,极化效应也对S 产生影响,从而导致S 随温度呈非线性增加。图7b显示了H 与温度的关系,H=U+pV。当温度增加时,U 和pV 均增加,表现为H 随温度的增加而增加。图7c 为F 随温度的变化趋势。温度升高,U 和S 均不断增加,但ST 增加的速度大于内能U,根据F=U⁃TS 可知,F 随温度的增加而减小。此外,相同温度下共晶体系 的S、H 和F 绝 对 值 从 大 到 小 的 顺 序 为CL‑20/1,4‑DNI>ε‑CL‑20>1,4‑DNI。图7d 显示了Debye 温度与温度的关系。基于德拜模型计算了0~600 K 时CL‑20/1,4‑DNI 共 晶 和 共 晶 组 分 的CV‑T 曲 线,见图7e。尽管在相同温度下三者的Debye 温度仅有微小差异,但仍可以观察到CL‑20/1,4‑DNI 的Debye 温度介于两个纯组分之间。众所周知,Debye 温度与固体的许多物理性质有关,例如比热和熔点。从图7e 可见,0~600 K 时,三种晶体的CV值均随温度升高而升高。在环境温度和压力下,CL‑20/1,4‑DNI、ε‑CL‑20 和1,4‑DNI 晶体的CV分别为2232,621.43 J·mol-1·K-1和1607.49 J·mol-1·K-1,其 从 大 到 小 的 顺 序 为CL‑20/1,4‑DNI>ε‑CL‑20>1,4‑DNI。
从以上分析可以得到,对特定温度下的热力学函数值(S、H、F、CV),其大小顺序均为CL‑20/1,4‑DNI>ε‑CL‑20>1,4‑DNI。这与文献[19]通过热分析得到的热稳定性顺序相一致。
此外,还计算了300 K 下CL‑20/1,4‑DNI 共晶和共晶组分的振动模式对CV的累计贡献,见图8 和表6。以CL‑20/1,4‑DNI 共晶为例,发现晶格振动对CV的贡献最大,为1010.038 J·mol-1·K-1,其次是“入口模”区(317.835 J·mol-1·K-1)和内振动A区(750.039 J·mol‑1·K-1),这三个频段占比高达95.39%。同样地,1,4‑DNI 和ε‑CL‑20 晶体也表现出了相同的规律,即晶格振动区对CV的贡献最大,“入口模”区和内振动A 区次之。显然,对CV的主要贡献源自0~33.28 THz 区域的低频声子,而内振动B 和C 区对CV的贡献很小,因此低频声子支配了热传导过程。由此可推测,CL‑20/1,4‑DNI 共晶和共晶组分由能量转移引起的化学键断裂经历了“多声子向上泵浦”过程。
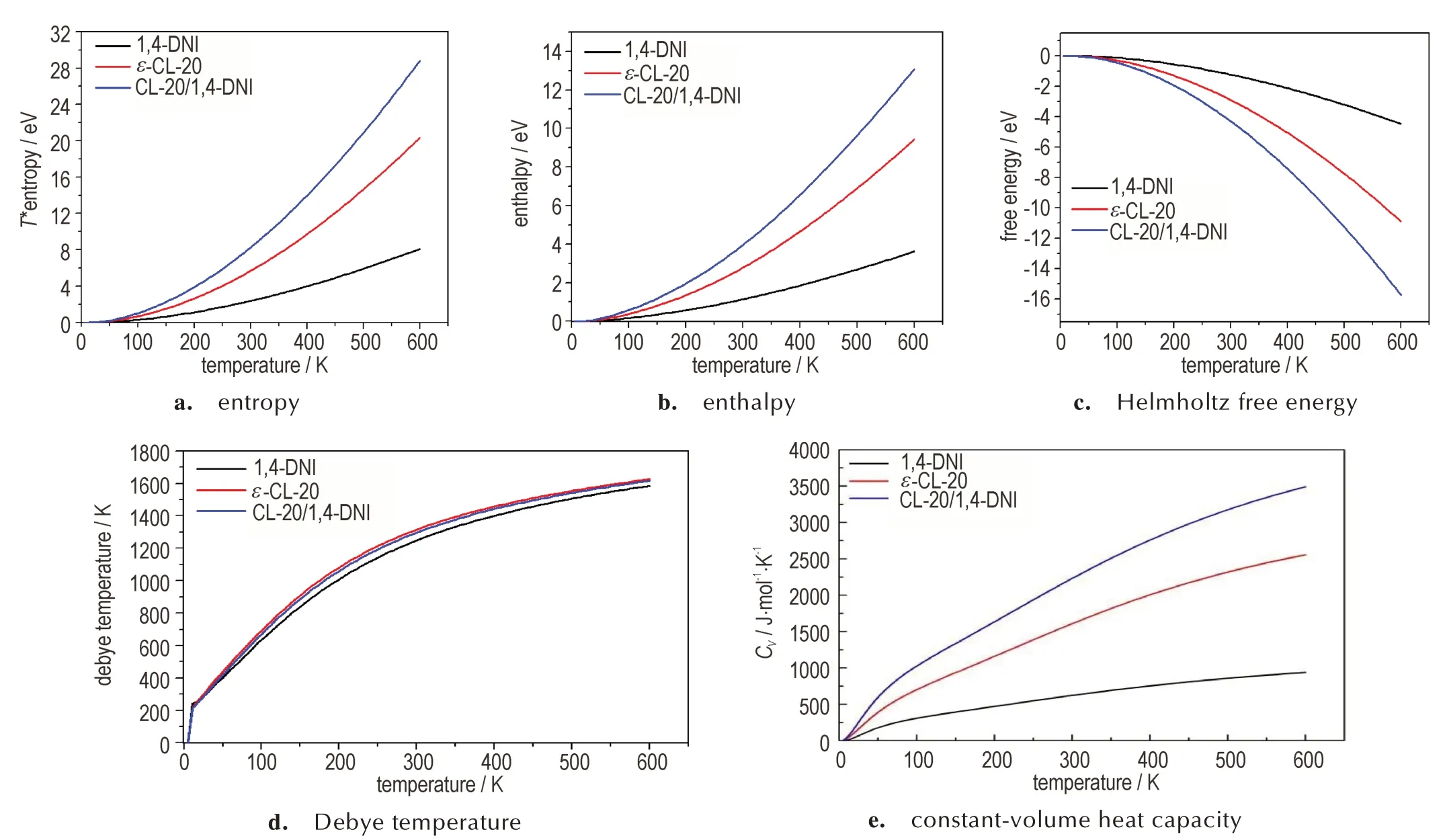
图7 CL‑20/1,4‑DNI、1,4‑DNI 和ε‑CL‑20 晶体的热力学函数值随温度的变化关系Fig.7 Functional values of the thermodynamics as a function of temperature in CL‑20/1,4‑DNI,1,4‑DNI and ε‑CL‑20 crystals
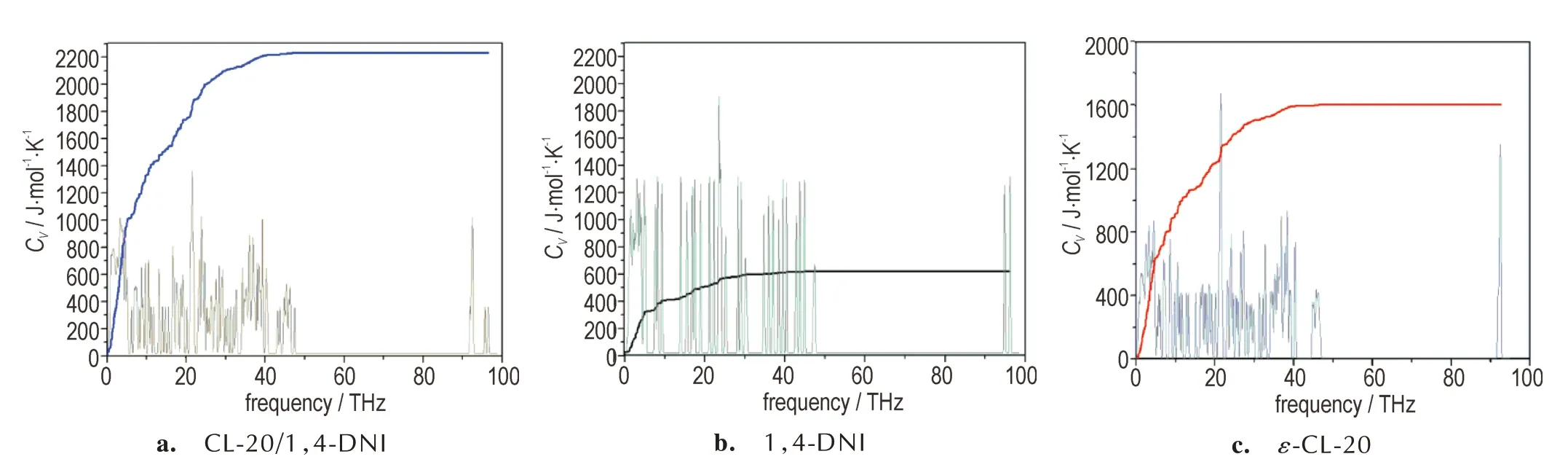
图8 300 K 下振动模式对CV的贡献Fig.8 Cumulative contributions of vibration modes to the heat capacity at 300 K
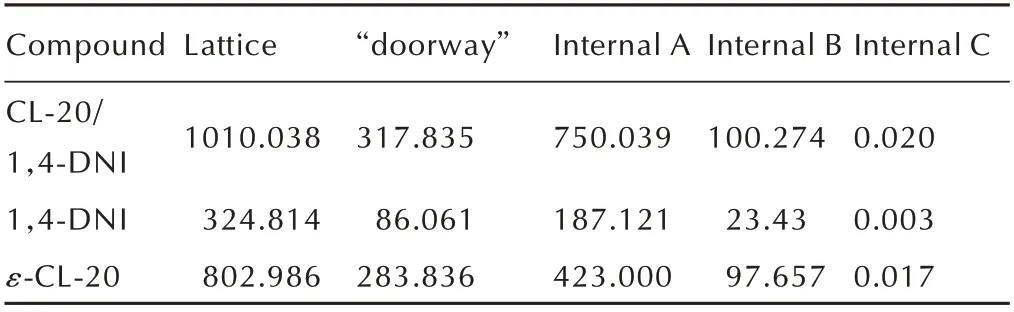
表6 300 K 下CL‑20/1,4‑DNI、1,4‑DNI 和ε‑CL‑20 晶体的振动模式对CV的贡献Table 6 Contributions of vibration modes to the heat capaci‑ty in CL‑20/1,4‑DNI,1,4‑DNI and ε‑CL‑20 crystals at 300 K J·mol-1·K-1
4 结论
运用DFT‑PBE 方法结合TS 色散校正计算了CL‑20/1,4‑DNI 共晶及共晶组分的声子谱,通过声子谱的分析可得到如下结论:
(1)1,4‑DNI、CL‑20/1,4‑DNI 和ε‑CL‑20 在 布里渊区中心点附近没有虚频,其带隙分别为46.17,43.29 THz 和44.13 THz;计算得到的“入口模”声子数分别为:13、26 和44,与撞击感度线性正相关;特征振动频率Δωd分别为:46.919,15.203 cm-1和4.858 cm-1,与撞击感度线性负相关。
(2)能量在ε⁃CL‑20 晶体中的流动方向为:外界刺激后过剩的热能和机械能首先转移到CL‑20 的硝基上发生振动弛豫,产生热声子。热声子与相邻原子发生非协耦合,促使能量从硝基流到N─N 键,最后流至笼形骨架上的其它原子,据此推测CL‑20 晶体的引发键为N─NO2。1,4‑DNI 晶体中能量流动方向为从硝基经C─N 和N─N 键流入咪唑环内,初始分解过程可能与咪唑环的开环反应有关。通过对比CL‑20/1,4‑DNI 共晶和共晶组分的声子态密度,推测共晶的初始热分解引发键为CL‑20 分子的N─NO2键。且形成共晶后,CL‑20 分子和1,4‑DNI 分子的热稳定性均得到改善,从而导致共晶的热稳定性优于两个单体。
(3)Debye 温度、S、H 和CV随温度的升高而增大,F 随温度的升高而减小。相同温度下热力学函数值的顺序为CL‑20/1,4‑DNI>ε⁃CL‑20>1,4‑DNI。通过计算振动模式对CV的累计贡献可以得出,低频声子对CV的贡献高达95.39%,由此推断由能量转移引起的化学键断裂经历了多声子向上泵浦过程。

