机器人用精密减速器空载摩擦转矩分析与测量

徐 航，何元春，吴耀庭，施 军，谢桂平，赵新宇

（1.中原工学院 a机电学院；b计算机学院，郑州 450007；2.宁波夏厦齿轮有限公司，浙江宁波 315202）

精密减速器具有传动精度高、效率高、传动比大、刚度大、体积小等优点，被广泛应用于工业机器人等领域［1-2］。工业机器人应用减速器主要有RV减速器、谐波减速器和行星减速器。精密减速器的性能对工业机器人的性能有直接影响。工业机器人的主要技术参数包括几何参数、运动学特性、负载特性、精度特性和重复性等。其中，几何参数如工作空间等特征是通过机器人的关节参数来表征的；加速、位置稳定时间等运动学特性则取决于精密减速器的背隙、扭转刚度和转矩密度；负载特性由精密减速器的扭转刚度、力矩负载和转矩密度决定；精度、重复性与精密减速器的精度、可重复性直接相关［3］。

精密减速器的非线性摩擦特性是造成工业机器人迟滞特性的重要原因。国标GB/T 35089—2018将空载摩擦转矩作为精密减速器的重要性能指标，通常需在出厂前进行测量评定，它是指在空载稳定转速下精密减速器的摩擦转矩［4］。目前，工业领域通常在空载状态下从输入端启动精密减速器，在不同转速下采集输入转矩及转速，绘制转矩 转速曲线，获得精密减速器的空载摩擦转矩特性，见式（1）。

式中：T为空载摩擦转矩；ω为转速；c为常数。

部分学者从测量和控制的角度出发，研究了精密减速器的摩擦特性。吕明帅［5］分析了RV减速器的摩擦特性，建立了静摩擦力+Coulomb+Strick+Stribeck摩擦模型；黑沫［6］分别基于 Stribeck静态摩擦模型和LuGre动态摩擦模型，研究了谐波减速器的摩擦特性；Prasanna等［7］基于LuGre动态摩擦模型研究了谐波减速器的摩擦特性及控制策略。大量实践表明：从低速到高速的整个过程，精密减速器的空载摩擦转矩与转速并不是线性关系，而是呈现出典型的Stribeck效应。因此有必要对精密减速器的空载摩擦转矩进行深入分析和测量。

本文中对精密减速器的空载摩擦特性与模型进行分析，介绍了空载摩擦转矩的测量原理，并进行从低速到高速的测量实验，为精密减速器的空载摩擦转矩性能测量与评价提供参考依据。

1 精密减速器的空载摩擦性能分析与建模

1.1 精密减速器的空载摩擦性能分析

采用油脂润滑的精密减速器，其摩擦特性呈现出典型的Stribeck效应，即摩擦转矩在低速阶段随转速的增加而减小，当大于一定的转速时，摩擦转矩随转速的增加而增加［8-9］，如图 1［10］所示。

根据Stribeck摩擦理论，为了描述精密减速器在低速阶段的Stribeck现象，将精密减速器的摩擦特性分为以下4个阶段：

1）静摩擦阶段：在驱动力矩未达到最大静摩擦力矩之前，精密减速器尚未转动，摩擦转矩主要由弹性变形所产生。

2）边界润滑阶段：精密减速器啮合副之间的润滑膜尚未建立，仍为固体到固体接触。

3）流体润滑阶段：接触表面间形成液体薄膜，但接触面未被润滑剂完全分开，仍有区域为固体接触［2，11-12］。

4）全流体润滑阶段：物体间的液体薄膜完全形成，没有固体接触的区域，摩擦转矩主要取决于速度和润滑剂的黏性系数，摩擦转矩随转速的增加而增加［2，11-12］。

1.2空载摩擦转矩 转速曲线模型

目前，国内外的学者通常采用Tustin模型、Gaussian模型、Lorentzian模型来描述 Stribeck效应［10，13］，如式（2）～（4）所示。

Tustin模型：

其中：Tf（ω）为摩擦转矩；Tc为库伦摩擦转矩；Ts为静摩擦转矩；ωs为Stribeck转速；B为黏滞摩擦因数；sign（ω）为符号函数。

以上3个模型均为静摩擦模型，其中Stribeck转速ωs可用于描述Stribeck曲线的形状。基于空载摩擦转矩的实际测量数据，采用合理的数据拟合方法可以获得精密减速器精确的空载摩擦转矩—转速曲线。

当需要对精密减速器的摩擦特性进行精确控制时，由于 Tustin模型、Gaussian模型、Lorentzian模型均为非线性模型，存在参数识别困难等问题，因此工业领域通常基于双直线模型进行控制，即将低速阶段、高速阶段的摩擦转矩 转速曲线分别做线性化处理，如图2所示。其中T1、T2的表达式见式（5）。

2 测量原理

在精密减速器综合性能测量仪上测量精密减速器的空载摩擦转矩时，其测量原理如图3所示。精密减速器的输入端由伺服电机驱动，并控制其工作在速度模式下，保证测量时转速稳定、输出端空载。

在精密减速器运转平稳时，其空载摩擦转矩等价于精密减速器的输入转矩，如式（6）。精密减速器输入端的转矩通过输入端扭转传感器测量获得。

其中：Tf为精密减速器的空载摩擦转矩；Tin为输入端转矩。

由于精密减速器不同啮合位置处的受力不同，导致精密减速器不同啮合位置的摩擦转矩不同，在输出端一转范围内，摩擦转矩呈周期性变化。对精密减速器输出端一转范围的扭矩信号进行均值滤波处理，即取扭矩的均值作为该转速下的摩擦转矩［14］，获得摩擦转矩与转速的一一对应关系，见式（7）。

3 实验分析

基于精密减速器综合性能测量仪（图 4）［2，15］，对某型号的RV减速器进行空载摩擦转矩测量实验。被测RV减速器的传动比为121，额定扭矩为784 N·m，额定转速为15 r/min。

3.1 空载摩擦转矩测量

在设定工况（设定转速、空载）下，由于不同啮合位置处精密减速器的受力不同，导致在输出端一转范围内摩擦转矩呈周期性变化。例如在输出端转速为2.094 ras/s时，测得输入端转矩如图5所示，表现出摩擦转矩随啮合位置的变化而变化。根据式（7），由计算可得该测量转速下的RV减速器的空载摩擦转矩为0.208 8 N·m。

3.2空载摩擦转矩—转速曲线

为了准确获得精密减速器的Stribeck摩擦效应，分别进行低速到高速的摩擦转矩测量实验。在低速阶段，测量间隔设置较小，高速阶段测量间隔可适当增大。测量获得的RV减速器的摩擦转矩—转速如图6所示。

基于Tustin模型，采用最小二乘法进行曲线拟合，获得所测RV减速器的空载摩擦转矩—转速曲线如图7所示。拟合获得模型的各项参数如表1、2所示。

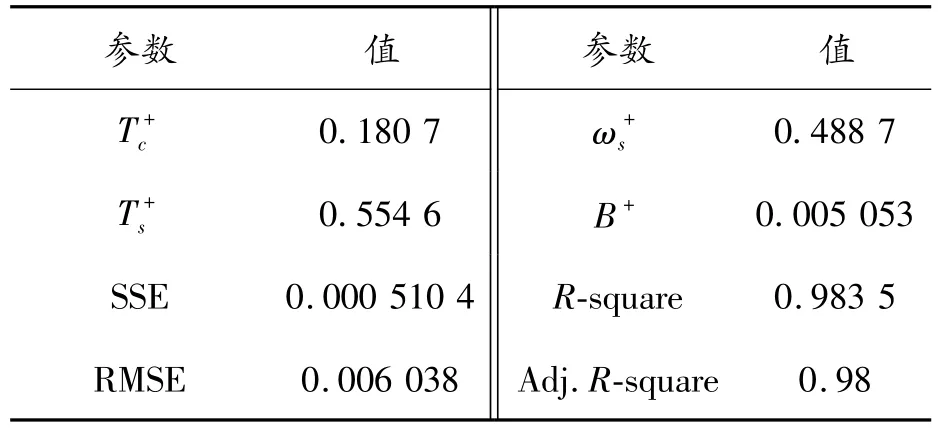
表1 RV减速器的正向拟合参数（Tustin模型）

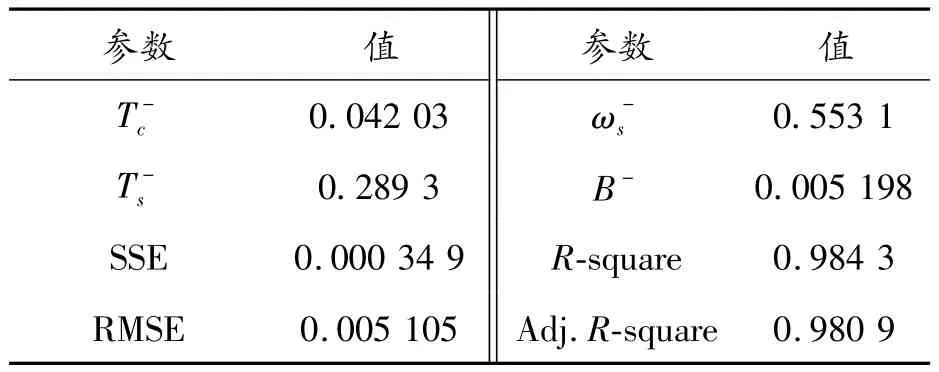
表2 RV减速器的反向拟合参数（Tustin模型）

基于Gaussian模型，采用最小二乘法进行曲线拟合，获得所测RV 减速器的空载摩擦转矩—转速曲线如图8所示，拟合获得模型的各项参数如表3、4所示。

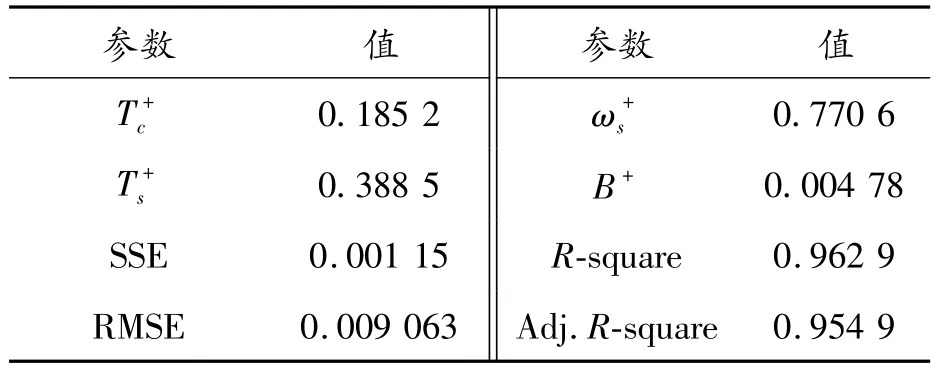
表3 RV减速器的正向拟合参数（Gaussian模型）

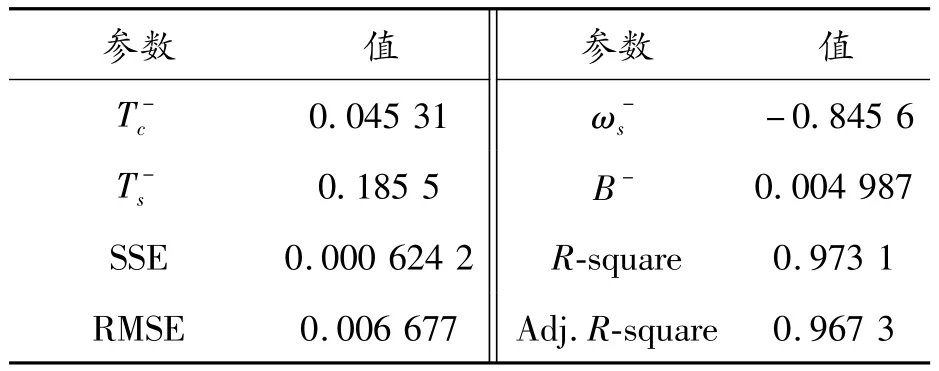
表4 RV减速器的反向拟合参数（Gaussian模型）

基于Lorentzian模型，采用最小二乘法进行曲线拟合，获得所测RV 减速器的空载摩擦转矩—转速曲线如图9所示。拟合获得模型的各项参数如表5、6所示。

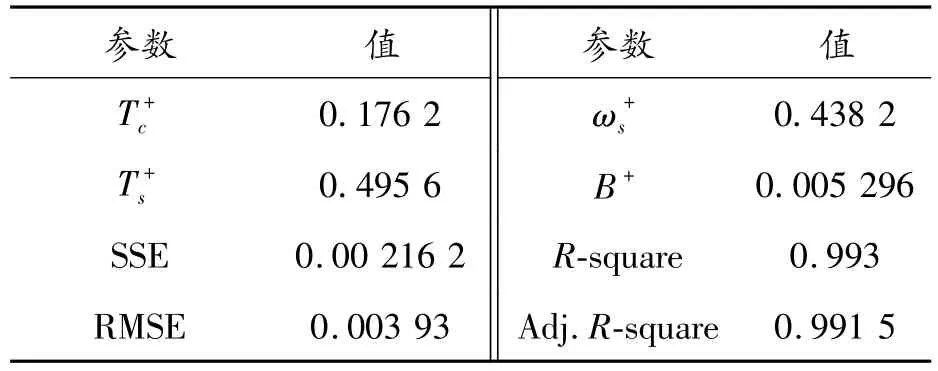
表5 RV减速器的正向拟合参数（Lorentzian模型）

表6 RV减速器的反向拟合参数（Lorentzian模型）

3.3 拟合效果对比

对比Tustin模型、Gaussian模型和Lorentzian模型的拟合结果，可以看出3个模型的校正决定系数（Adj.R-Square）均接近1，均达到理想的拟合效果。

3个模型中，Lorentzian模型正反向的拟合参数 SSE、RMSE均最小，R-square、Adjusted R-square均最大，说明Lorentzian模型的拟合效果最佳，更适合精密减速器空载摩擦性能分析。

4 结论

1）精密减速器的空载摩擦转矩与转速呈现出典型的Stribeck效应，在低速阶段摩擦转矩随转速的增加而减小；在高速阶段，摩擦转矩随转速的增加而增加。

2）Lorentzian模型可以精确描述精密减速器的Stribeck效应，具有理想的拟合效果。