浅谈常微分方程在数学模型中的应用及其数值模拟
史诗洁 吕羽 张红梅


[摘 要]常微分方程是重要的数学理论,在实际中具有广泛的应用,也是数学建模的重要理论之一。基于培养“应用型”“创新型”人才的实际需求,结合实际问题—人口预测问题,分析在数学理论的课堂教学中,如何将理论知识应用于实际问题中,使学生了解数学理论的实际应用,加深学生的理解与记忆;以及在数学建模课堂的教学中,如何选择恰当的教学内容,使学生快速掌握建模方法。
[关键词]数学模型;常微分方程;分离变量法;人口模型;数值模拟
[基金项目]2018年度深圳技术大学教改研究项目“数学建模课程建设的探索”(2018.11:2018105101035);2018年度深圳技术大学教改研究项目“新工科背景下基于LEGO Mindstorms机器人系统的大学计算机基础课程创新教学的研究”(2018.11:2018105101031);2020年度深圳技术大学教改研究项目“面向应用型人才的启发与实践有机结合的数学教学新模式探究”(2020.01:202018666601012)
[作者简介]史诗洁(1990—),女,广东汕头人,博士,深圳技术大学大数据与互联网学院讲师,主要从事趋化系统解的性态研究;吕 羽(1983—),男,广东深圳人,博士,深圳技术大学大数据与互联网学院副研究员,主要从事机器学习算法研究;张红梅(1973—),女,黑龙江齐齐哈尔人,博士,深圳技术大学大数据与互联网学院副教授,主要从事数学基础学科和应用学科的教学和研究工作。
[中图分类号] G642;O13-4 [文献标识码] A [文章编号] 1674-9324(2020)45-0-02 [收稿日期] 2020-05-19
一、引言
數学是科技发展的重要理论基础,在高等教育中占有重要的地位。其中,常微分方程是大部分理工专业的必修课程。客观世界是实时变化的,常微分方程正是描述这种变化规律的主要工具。在高等教育中,使学生掌握理论知识只是最基本的要求,而理论的实际应用才是最终目的。本文以常微分方程[1]中最基本的类型—可分离变量方程为例,结合人口模型,说明如何将常微分方程理论应用于实际问题。对于大学理工科一年级的学生,该模型所需的预备知识以及求解方法是他们在高等数学的课堂中刚刚结束学习以及正在学习的内容,印象深刻,比较容易理解和掌握,因此学生的注意力将完全集中到整个建模的流程上,快速理解数学建模的目的,以及所学的数学理论在数学建模和实际问题中的应用价值。
二、常微分方程基础理论
若一阶微分方程F(x,y,y)=0可写f (x)dx=g(y)dy,则称为可分离变量方程。可分离变量方程的名称中隐含其求解方法:
首先,对方程进行变量分离,即将两个变量x和y分别归拢到等式两侧,得
其次,对(1)式等号两侧同时积分,得到
若等号两侧的积分都存在,则(1)有隐式通解F(x)=G(y)+C,其中C是积分常数。
三、微分方程在数学建模中的应用
常微分方程的应用领域非常广泛,无论在基础科学、应用科学和社会科学中都可以找到常微分方程的影子,例如:电磁学,流体力学,海洋动力学,控制科学等。本文以社会科学中的人口预测问题为例,说明其应用。
1798年,英国人口学家马尔萨斯提出了马尔萨斯(Malthus)人口模型[2,3]
其中x(t)表示t时刻人口,r表示人口增长率。显然上式是可分离变量方程,可以解得
x(t)dx=x(0)ert
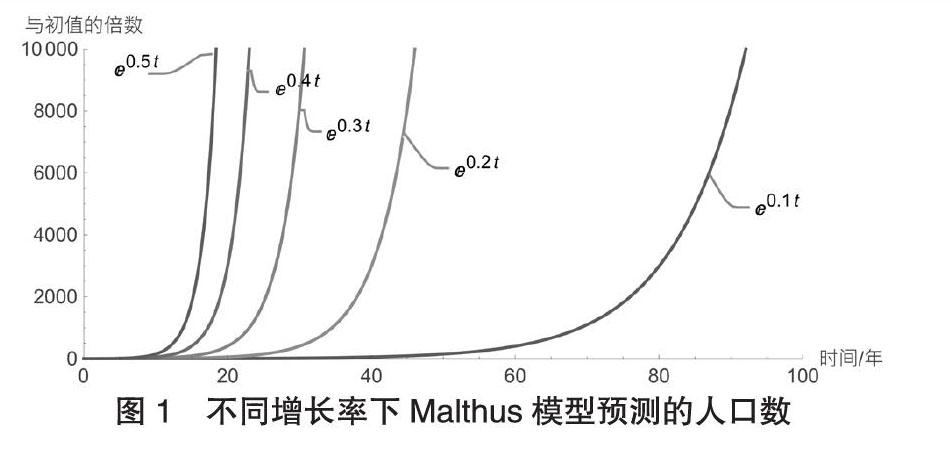
上式表明,自然增长率r一旦取定,按马尔萨斯模型预测的人口数将以指数形式增长,如图1所示,这显然与实际情况是相悖的。这是源于马尔萨斯认为生产资料对人口增长的限制是“弹性”的,因此人口增长率基本维持在一个稳定水平[3]。然而,人口增长数不仅受限于资源,还受环境承载力的影响,包括国家政策,地理环境,经济发展水平,生态环境等。
其中,M为最大人口容量,为人口增长率。这同样是一个可分离变量方程,其解为
基于Malthus模型与Logistic模型对1949—2020年全国人口数的预测以及实际人口数[6],本文运用数学软件进行数值模拟,如图2所示。可以看出,Logistic模型自始至终可以准确预测实际的人口数量,而Malthus模型在1980年以后逐渐偏离实际的人口数,而且趋势是无限上升,与实际情况相悖。在实际的课堂教学中,通过这个例子让学生明白要解决实际问题,需要考虑实际情况中的影响因素,建立实用的数学模型。
虽然从图2中还可以看到,至目前为止(2020年),Logistic模型可以准确预测实际的人口数量,但是随着社会的进步,人们对人口数量发展规律的认识不断加深,人口发展问题还应考虑其他因素的影响,例如生育率、性别比例、社会年龄结构、环境承载力、生活必需品等。考虑到上述因素的影响,Logistic模型中还存在哪些不足?在课程结束时,可以引导学生去发现问题,并通过改进模型来解决问题。这也是我们开设数学模型课程的初衷。
参考文献
[1]同济大学数学系.高等数学[M].第7版.北京:高等教育出版社, 2014:303.
[2]姜启源.数学建模[M].第5版.北京:高等教育出版社,2005:141.
[3] [英]马尔萨斯.人口原理[M].朱泱,等,译.北京:商务印书馆, 1992:1.
[4]王学保,蔡果兰.Logistic模型的参数估计及人口预测[J].北京工商大学学报(自然科学版),2009(27):75-78.
[5]顾樵.数学物理方程[M].北京:科学出版社,2015:2.
[6]国家统计局[DB/OL].http://data.stats.gov.cn/index.htm.
The Application of Ordinary Differential Equation and Its Numerical Simulation in Mathematical Model:
Taking Population Model as an Example
SHI Shi-jie, L? Yu, ZHANG Hong-mei
(College of Big Data and Internet, Shenzhen Technology University, Shenzhen, Guangdong 518118, China)
Abstract: Ordinary differential equation is an important field in mathematics, which is widely used in practice, and is also one of the important theories of mathematical modeling. Based on the needs of applied universities to cultivate "applied" and "innovative" talents, this paper introduces a method about applying theoretical knowledge to practical problems in mathematical classes, which helps students to understand the practical application of mathematical theory, and deepens their understanding and memory. Moreover, this paper also introduces how to choose the appropriate content to make students master the modeling method quickly in the mathematical modeling class. For more details, the authors choose the population model as an application example mainly because the modeling principle of the model is simple and the method is intuitive.
Key words: mathematical modeling; ordinary differential equation; separation of variables; population model; numerical simulation

