一类阻尼控制半主动隔振系统的解析研究1)
张婉洁 牛江川,2) 申永军 杨绍普 王 丽
∗(石家庄铁道大学交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043)
†(石家庄铁道大学机械工程学院,石家庄 050043)
引言
隔振是一种有效的振动控制方式,通过在振源和隔振对象之间合理设计隔振装置,选择合适的隔振系统的阻尼或者刚度,使得振源传至隔振对象的力或运动激励降低,减小外部扰动向系统敏感部分的传递,达到良好的隔振效果[1-2].传统的被动隔振系统结构和参数一旦确定就无法改变,无法满足复杂多变的工况条件,也无法协调共振响应与高频衰减之间的矛盾,制约了被动隔振系统性能的进一步提高.主动隔振系统减振效果好,但是成本高、能量消耗大、结构复杂.而基于半主动控制的隔振系统具有被动控制简单易操作和主动控制良好的隔振性能的优势,近年来在车辆悬架减振系统、高精密机械系统、飞机着陆装置、建筑结构振动控制系统、船舶的可控浮阀隔振系统中得到了广泛的应用[3-7].
半主动控制属于参数控制,根据一定规则来实时改变结构的刚度或阻尼等参数,进而提高隔振系统在不同激励下的隔振性能,控制过程依赖于结构反应及外部激励信息.相对于变刚度,采用电子控制阻尼调节的方法来实现阻尼控制更为容易,目前已有很多成熟的可控阻尼器,如电流变阻尼器和磁流变阻尼器等.在隔振系统的半主动控制中,控制策略直接决定着隔振系统的隔振效果.Karnopp 等[8]在1974 年首次提出了半主动悬架系统速度负反馈的“天棚”(sky-hook,SH)阻尼控制算法;Margolis 等[9-10]在天棚阻尼控制的基础上提出了开关控制,即阻尼力与相对速度的乘积为正,则阻尼器从悬架系统吸收能量,起到减振的效果;反之表示阻尼器要向悬架系统提供能量.Valasek 等[11]根据SH 原理,提出了与SH 算法相似的“地棚”(ground-hook,GH)阻尼控制算法,将非簧载质量与大地连接在一起,以大地作为系统坐标,目的是减小非簧载质量加速度;Savaresi 等提出了加速度驱动阻尼(acceleration driven damper,ADD)控制算法[12]用以优化簧载质量加速度,以及混合SH-ADD 控制算法[13-14],结合两种算法优势,在整个频域内提高车辆舒适性;Riccardo 等[15]提出了动力驱动阻尼器(power-driven-damper,PDD)算法.Nirala 等[16]提出了冲击驱动阻尼(jerk driven damper,JDD)控制算法,在突然刹车时能有效减小垂向加速度.Poussot-Vassal 等[17]对SH,GH,ADD,SH-ADD 等多种半主动悬架控制方法进行了综述.
开关控制的思想是在高阻尼和低阻尼之间切换来实现减振的效果.由于半主动开关控制算法简单、响应快、易于实现,并能实现较好的控制效果,在实际工程中有很好的应用前景.半主动控制系统中依据不同开关控制算法和切换条件,根据系统状态的不同来实现开、关两种不同状态下阻尼的快速切换,属于强非线性系统.其中,依据相对速度和不同变量的乘积作为切换条件的控制策略包括天棚阻尼控制算法、地棚阻尼控制算法和加速度驱动阻尼控制算法等.Shen 等[18]对4 种基于不同反馈的地棚阻尼控制策略的半主动吸振器进行了解析研究;D´ıaz 等[19]分析了3 种基于速度反馈的非线性开关控制在高增益和显著振级的振动下的饱和问题;Eslaminasab 等[20]研究了半主动相对控制的单自由度悬架系统的控制效果;申永军等[21-24]分别采用有限相对位移控制、天棚控制等策略对含有时滞的单自由度半主动悬架系统进行了动力学分析;Yu 等[25]分析了基于磁流变液阻尼器组成的天棚阻尼控制隔振系统的非线性和时滞特性;Fischer 等[26]分析了主动和半主动车辆悬架系统;王昊等[27]以某磁流变阻尼器作为作动器,研究了4种开关半主动控制策略对整车悬架系统参数的影响;Kim 等[28]对比了在不同激励下主动、半主动和混合质量调谐阻尼器的控制效果;Dong 等[29]对比分析了包括天棚阻尼控制、混合控制、滑模控制、LQG 控制和模糊逻辑控制等5 种磁流变半主动悬架的控制效果.目前,大多数研究是采用数值分析的方法对控制性能进行分析,而且针对多种半主动控制策略的对比分析较少.
本文从近似解析分析的角度,以含立方刚度的单自由度半主动隔振系统为例,通过平均法建立系统的近似解析解,进而对3 种基于相对速度反馈的半主动开关控制策略的动力学性能进行分析,利用Lyapunov 理论分析系统的稳定性;通过数值解和解析解的比较,验证解析结果的正确性;详细分析了3 种控制策略在简谐激励和随机激励下的控制效果.
1 近似解析解
1.1 数学模型
通常非线性半主动隔振系统都是基于“质量--弹簧--阻尼”结构体系来近似简化模型,其单自由度半主动隔振系统的模型[30]如图1 所示,可用一个并联的弹性元件和阻尼器来表示.此模型中,除线性刚度和线性阻尼外,引入非线性刚度,用以克服线性隔振技术的缺陷,改善系统隔振性能[25].可控阻尼通过传感器对系统状态进行判断后,依据不同的变化规律,在一定范围内对可控阻尼进行调节,从而达到减振的效果.具有这种形式的如1/4 车辆悬架系统、船舶浮阀减振系统等.以1/4 车辆悬架为例,图1 中m为车体质量,x为车体的位移,x0为路面激励,F1为非线性弹性力:F1=k1(x0−x)+k2(x0−x)3,其中k1表示线性刚度系数,k2表示非线性刚度系数;F2为阻尼力:F2=c(˙x0−˙x),其中c表示线性阻尼系数.
根据牛顿第二定律得系统的运动方程为

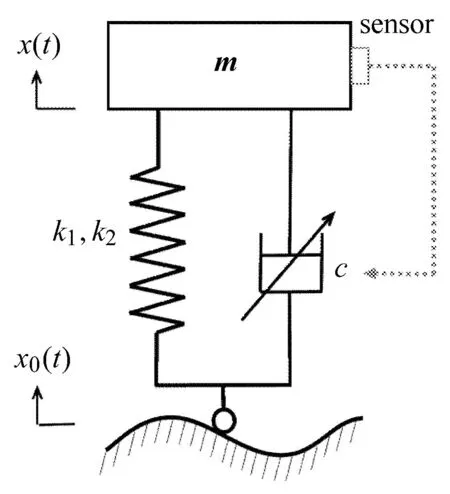
图1 单自由度半主动隔振系统模型Fig.1 Model of a single-degree-of-freedom semi-active vibration isolation system
令y=x−x0,路面激励取简谐激励x0=Acos(ωt),A为简谐激励的幅值,且为常数,ω 为简谐激励的角频率.代入式(1)得
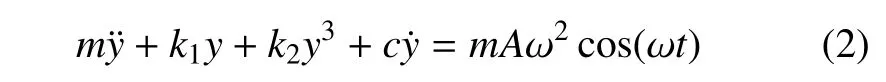
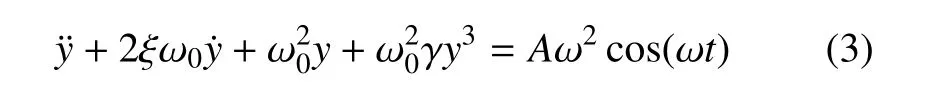
分析系统的主共振,即路面激励频率ω 接近系统固有频率ω0时的共振,引入ω2=+εσ(σ 为调谐参数),定量表示两个频率之间的接近程度,且限制ξω0=εµ,γ=εγ1,Aω2=εf,代入式(3)可得
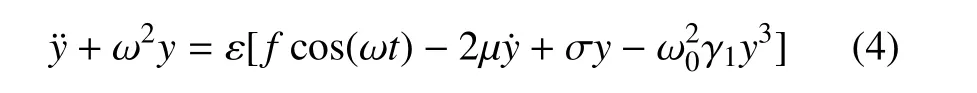
1.2 未加控制时的近似解析解
采用平均法求解方程的近似解析解[31],假设振幅a和相位ψ 是时间的慢变函数
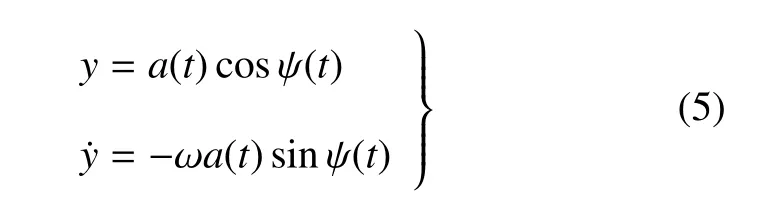
其中,ψ(t)=ωt+ϕ(t).根据平均法可得到一阶近似解振幅和相位满足的方程
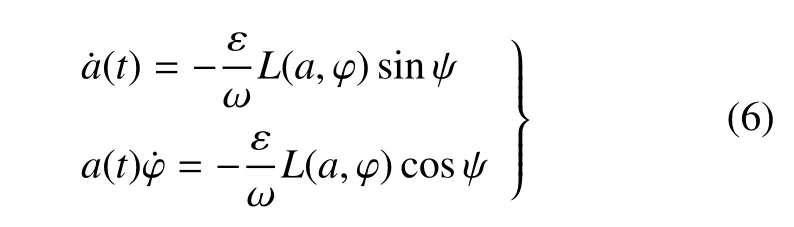
其中
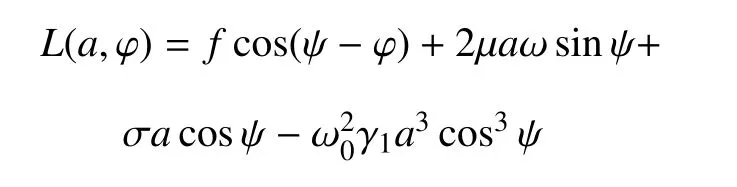
由于振幅和相位是随时间变化的ε 的同阶小量,可以将式(6)在一个周期内进行平均处理,得到近似解振幅和相位的显式,即
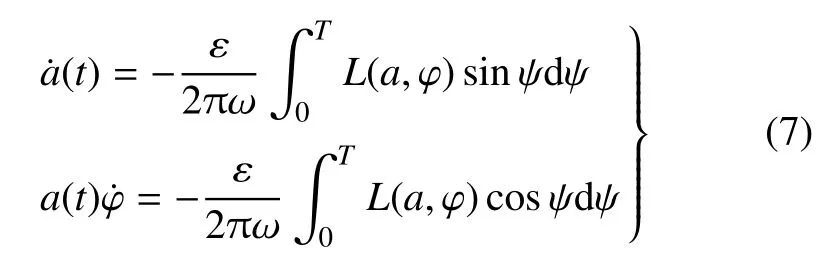
当不采取任何控制策略时,在一个周期[0,2π]内进行积分,得到幅值和相位的近似值为
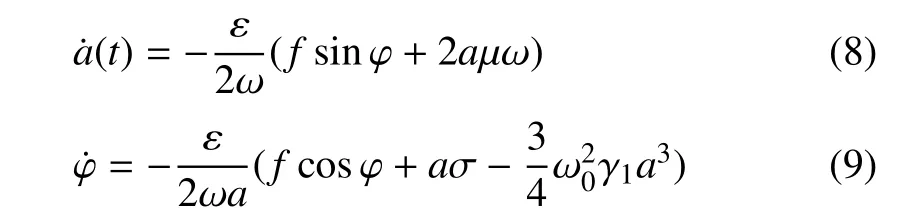
1.3 加速度驱动阻尼控制下的近似解析解
非线性隔振系统采用加速度--相对速度的加速度驱动阻尼ADD 的控制策略,根据簧载质量加速度和相对速度得出期望阻尼力,ADD 控制策略为
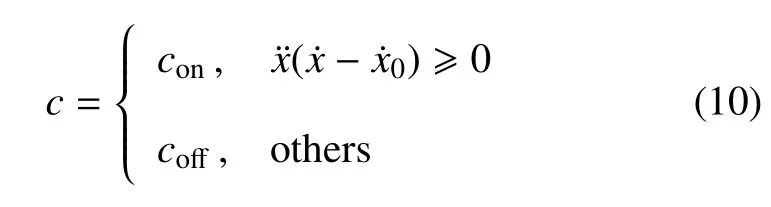
其中,con表示状态“开”时的阻尼系数,coff表示状态“关”时的阻尼系数.
根据前述对参数的定义,可利用定义的参数µ来表示控制策略,即参数µ需要根据系统变化进行调节
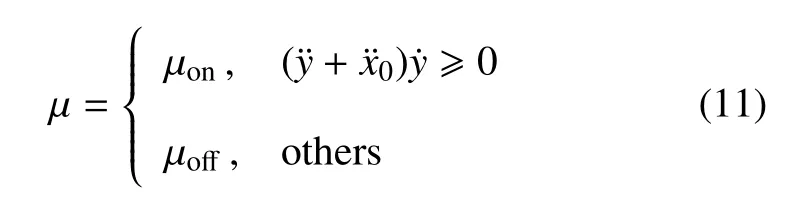
为简化判断条件,由于振幅a(t)和相位ϕ(t)随时间的变化是与ε 的同阶小量,与ψ(t)相比,是缓慢变化的,因此根据式(5)可近似取=−ω2acos ψ,则有
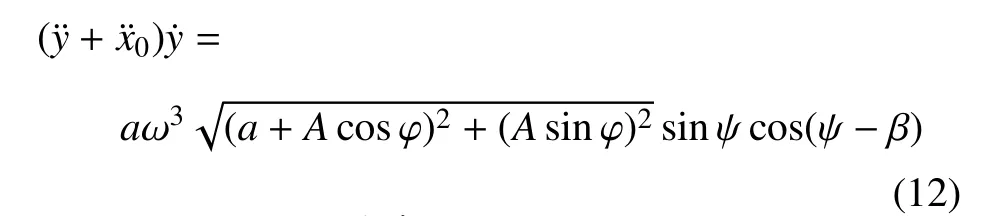
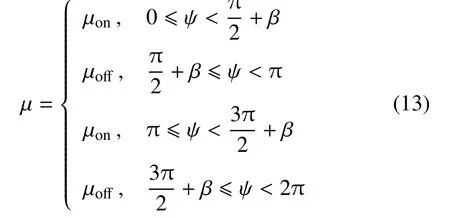
采用平均法,在一个周期内进行积分,可得振幅和相位的近似值为
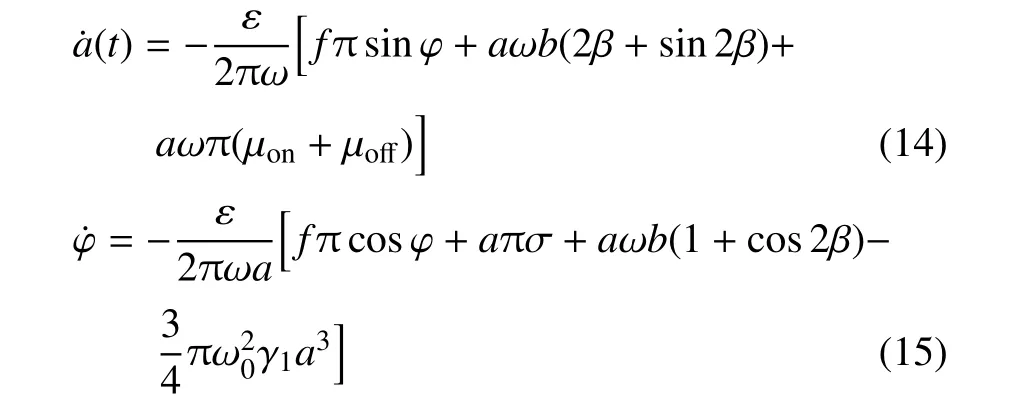
其中,b=µon−µoff.
1.4 天棚阻尼控制下的近似解析解
非线性隔振系统采用速度--相对速度的天棚SH 阻尼的控制策略为
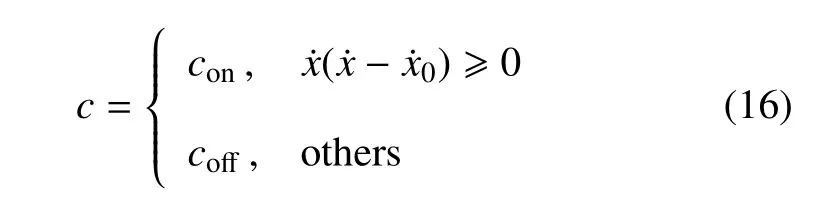
类似地可以得到采用SH 控制策略时,控制策略用参数µ表示为
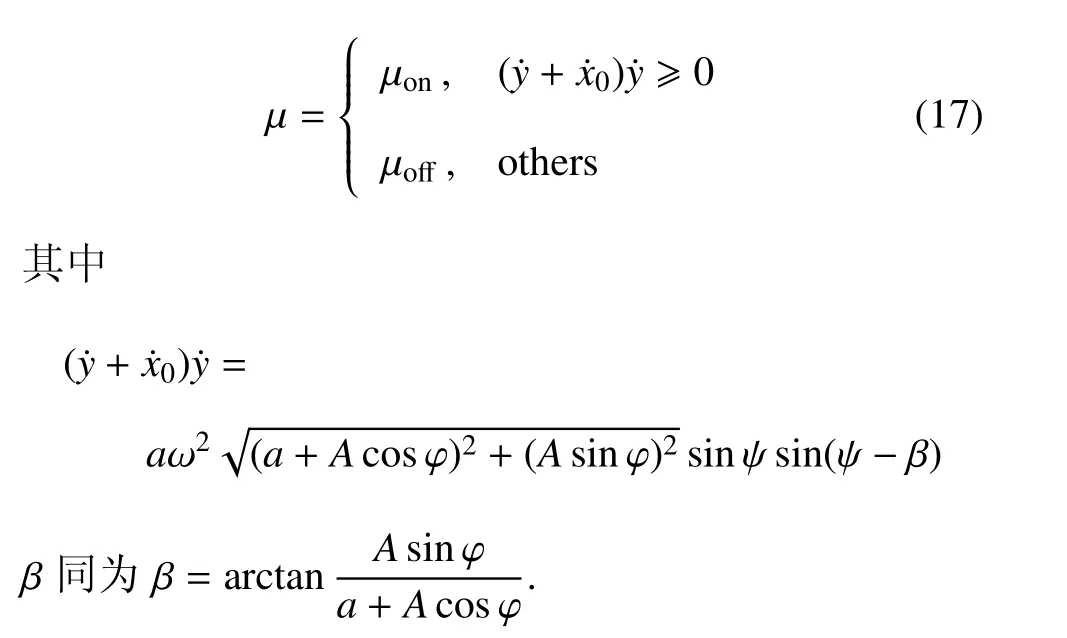
当β > 0 时控制策略在一个周期内的变化规律为

采用平均法,在一个周期内进行积分,可以得到:
当β>0 时,振幅和相位的近似值为

当β < 0 时,控制策略在一个周期内的变化规律为
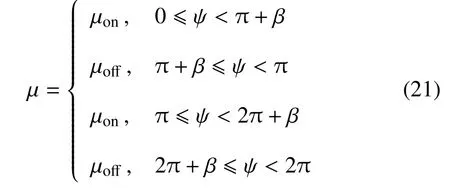
采用平均法,在一个周期内进行积分,可以得到当β<0 时振幅和相位的近似值为
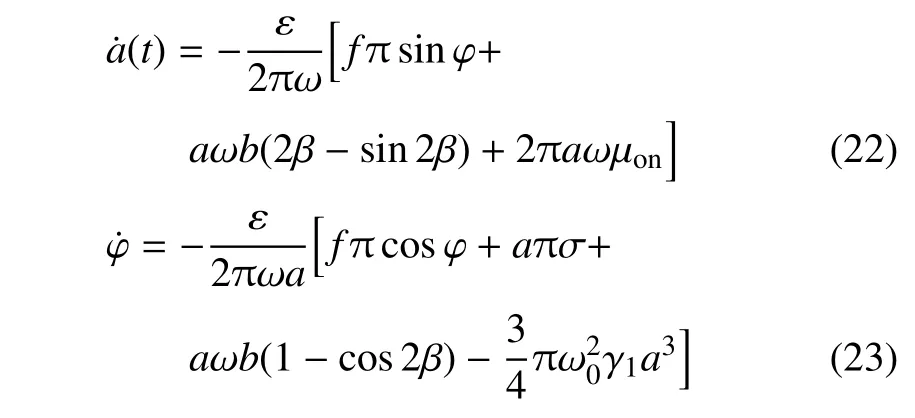
1.5 地棚阻尼控制下的近似解析解
非线性隔振系统采用位移--相对速度的地棚GH 阻尼控制策略为

类似地,采用GH 控制策略时,控制策略用参数µ表示为
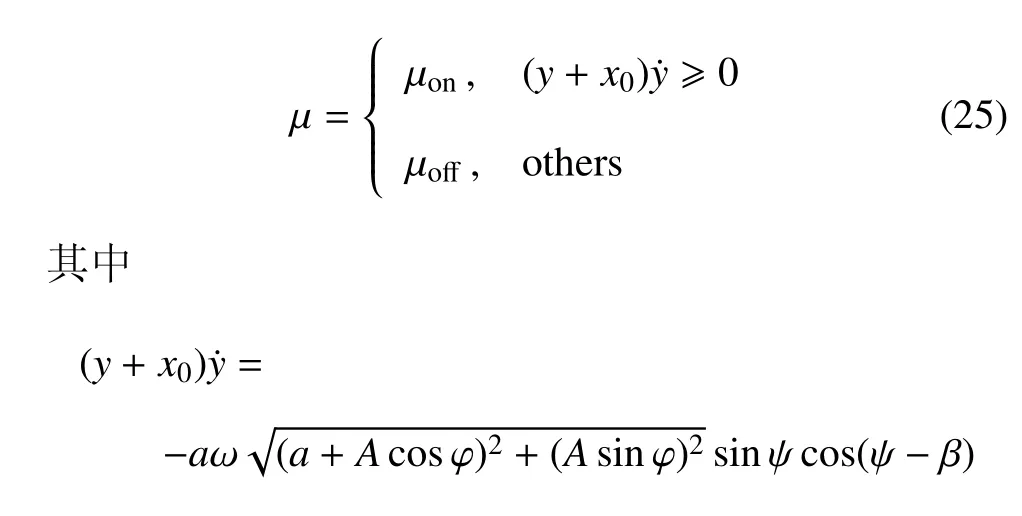

采用平均法,在一个周期内进行积分,可得振幅和相位的近似值为

2 定常解和稳定性分析
2.1 控制策略下的定常解
对于振动控制系统而言,系统的稳态运动更有意义.以下以ADD 控制的系统为例说明此类控制策略下的系统的定常解和稳定性分析.设ā 和分别表示稳态幅值和稳态相位,令式(14)和式(15)中(t)=0 和=0,可以得到系统的稳态方程组
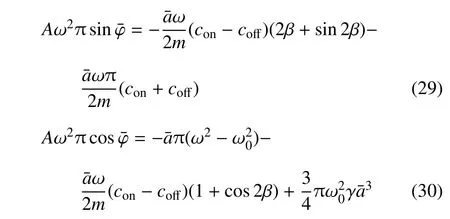
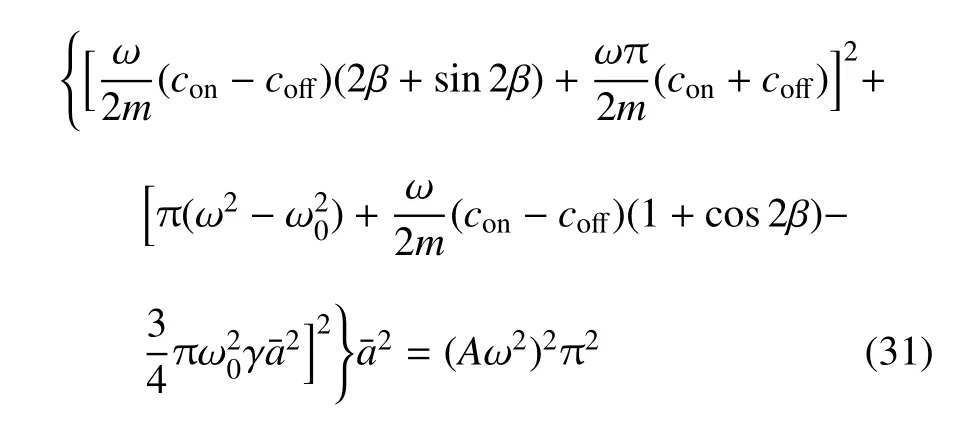
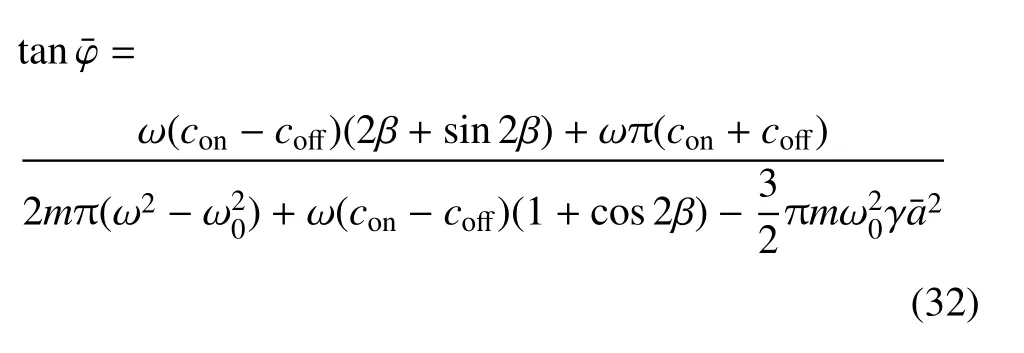
因此主共振的峰值即稳态振幅的最大值为

由于ω>0 解得主共振的骨架线方程为

类似可以得到在SH 控制下,β > 0 时稳态的幅频响应方程为
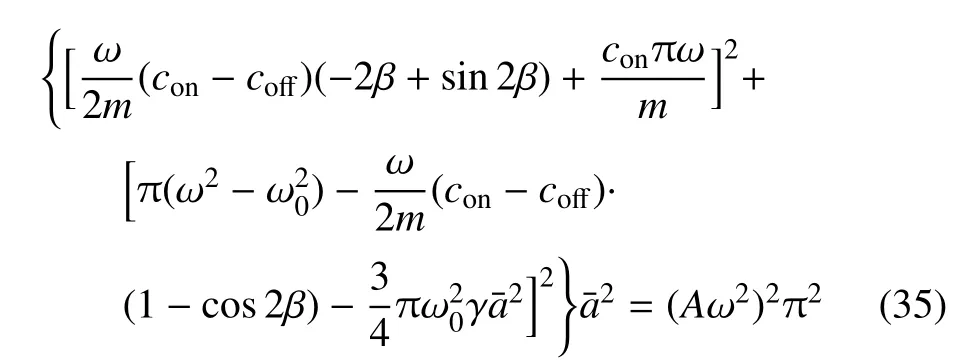
相频响应方程为

相频响应方程为
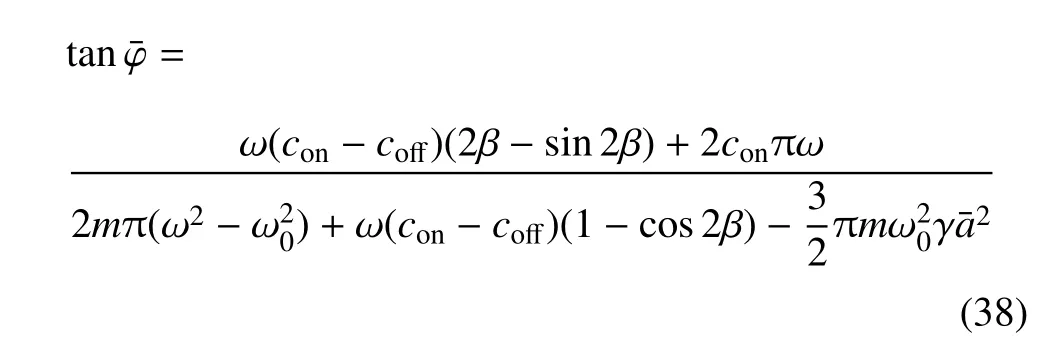
在GH 控制下,稳态的幅频响应方程为
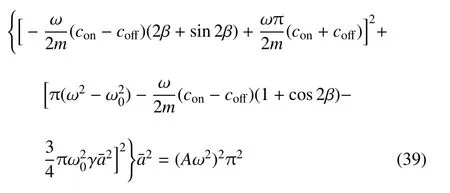
以及相频响应方程为
从试验结果可知,随着两种铁离子用量的增大,磁性产品的产率逐步升高。通过前面的反应式可知,矿浆中生成新的Fe3O4颗粒,并在赤铁矿表面形成物理吸附。随着亚铁离子与铁离子用量不断增大,赤铁矿表面吸附越来越多的Fe3O4颗粒。由于新的Fe3O4颗粒增强赤铁矿表面的磁性,间接使赤铁矿磁性不断增大,使其克服自身重力,被磁选机的磁场捕获,使得磁选的回收率增大。当亚铁离子和铁离子总用量为0.021 mol/L,赤铁矿回收率达到最大。

2.2 稳定性分析
对于ADD 控制的系统,采用Lyapunov 理论研究其稳态解的稳定性.对稳态解引入小扰动,令a=+∆a,ϕ=+∆ϕ,并代入式(14)和式(15)中,进行泰勒展开并略去高阶项,得
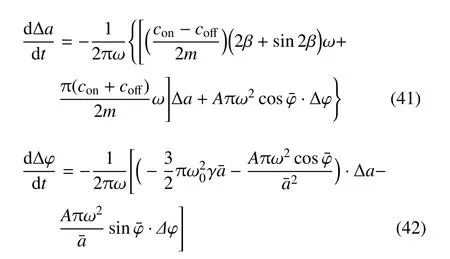

展开式(43),得到特征方程
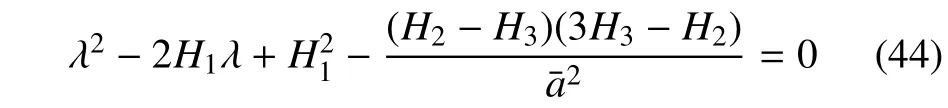
由于H1<0,因此得到系统周期解的稳定性条件为
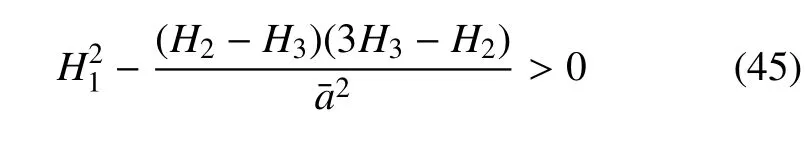
分析上式可知,当幅频特性曲线方程中存在3 个定常解时中间解为不稳定解,存在不稳定解的原因是在于弹性元件存在非线性刚度.若模型中不存在非线性刚度k2,那么式(43)中H3=0,则特征方程(44)可变换为
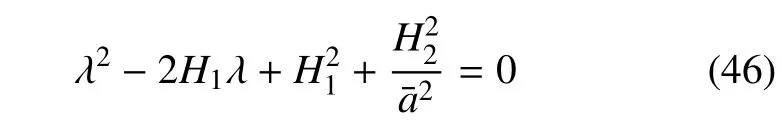
依据稳定性判定准则可知,系统定常解恒为稳定的.
类似地,对于GH 控制下系统周期解的稳定性进行分析,得到特征方程为
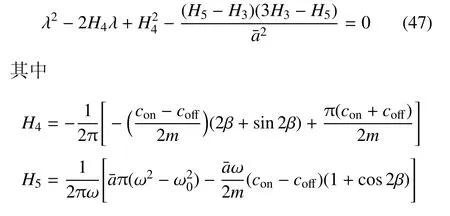
由于H4<0,因此得到系统周期解的稳定性条件为
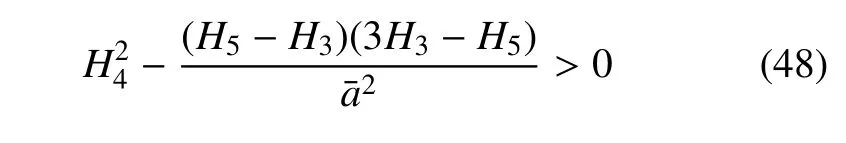
对于SH 控制下β > 0 时系统周期解的稳定性进行分析,得到特征方程为
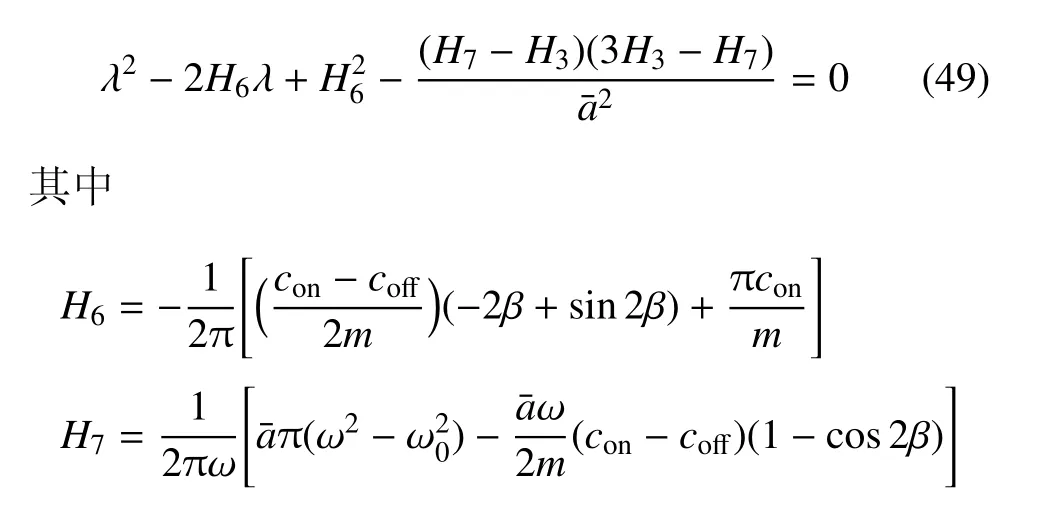
由于H6<0,得到系统周期解的稳定性条件为

β<0 时得到的特征方程为
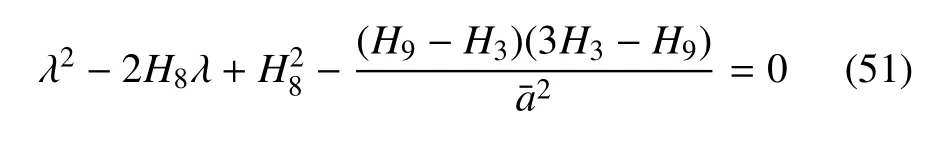
其中
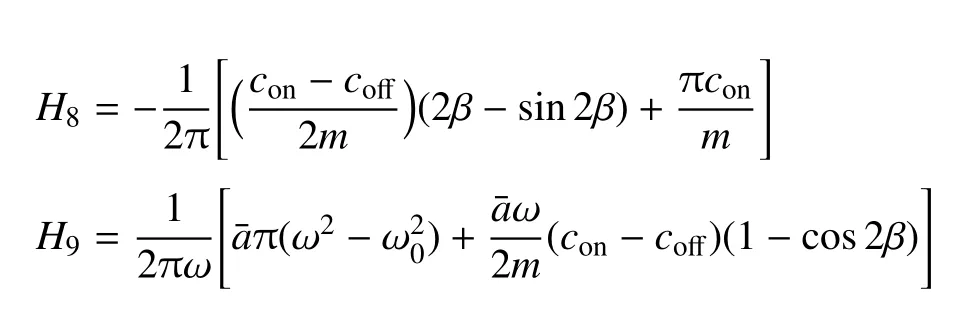
由于H8<0,得到系统周期解的稳定性条件为
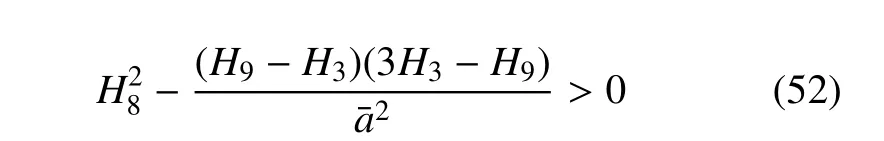
3 数值解验证
对于给定的某一悬架系统,取各参数为[32-33]:车体质量m=240 kg,弹簧线性刚度k1=16 000 N/m,非线性刚度k2=320 000 N/m.为对比在不同条件下近似解析解和数值解的吻合程度,在3 种不同控制策略下的开/关阻尼系数及路面简谐激励振幅取值略有不同.数值解的求解采用Runge-Kutta 法,计算时间为800 s,将后10%的响应的最大值作为稳态响应的幅值.图2 ∼图4 分别为在ADD、SH 和GH 控制策略下数值解和近似解析解得到的幅频响应曲线,图中横轴为激励频率ω,纵轴为响应振幅a.从图2 ∼图4 可以看出,3 种控制策略的解析解在不同的激励幅值和系统参数下,在低频区和共振区均和相应的数值解均具有较好的一致性,证明了系统解析解的求解方式的正确性和准确性.需要注意的是,由于半主动控制系统响应中存在高阶奇次谐波成分,因此在高频区可能会表现出颤振现象[23].

图2 ADD 下的幅频响应曲线Fig.2 Amplitude-frequency response with acceleration driven damper control(con=1500 N·s/m,coff=50 N·s/m,A=0.06 m)
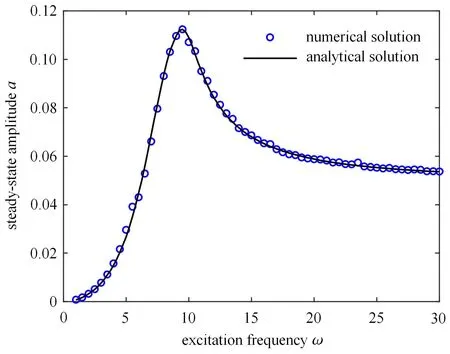
图3 SH 下的幅频响应曲线Fig.3 Amplitude-frequency response with sky-hook control(con=1000 N·s/m,coff=50 N·s/m,A=0.05 m)
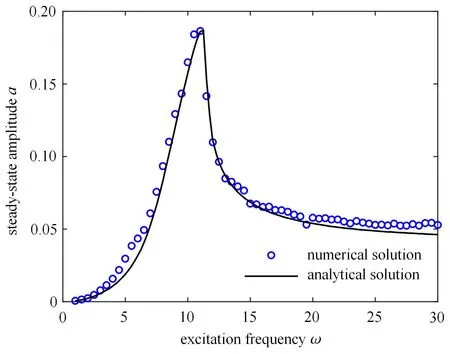
图4 GH 下的幅频响应曲线Fig.4 Amplitude-frequency response with ground-hook control(con=1000 N·s/m,coff=50 N·s/m,A=0.04 m)
4 控制效果分析
4.1 开关控制阻尼的变化分析
以ADD 控制为例,分析半主动开关控制的开/关阻尼变化时对主共振振幅的影响.
令coff=50 N·s/m 并且保持不变,con分别取500,1000,1500 和2000 N·s/m 时系统的幅频响应曲线如图5 所示.可以看出,增大阻尼con,系统在全频域内共振振幅都逐渐减小,而且系统的非线性特性被抑制,分析结果与式(33)吻合.
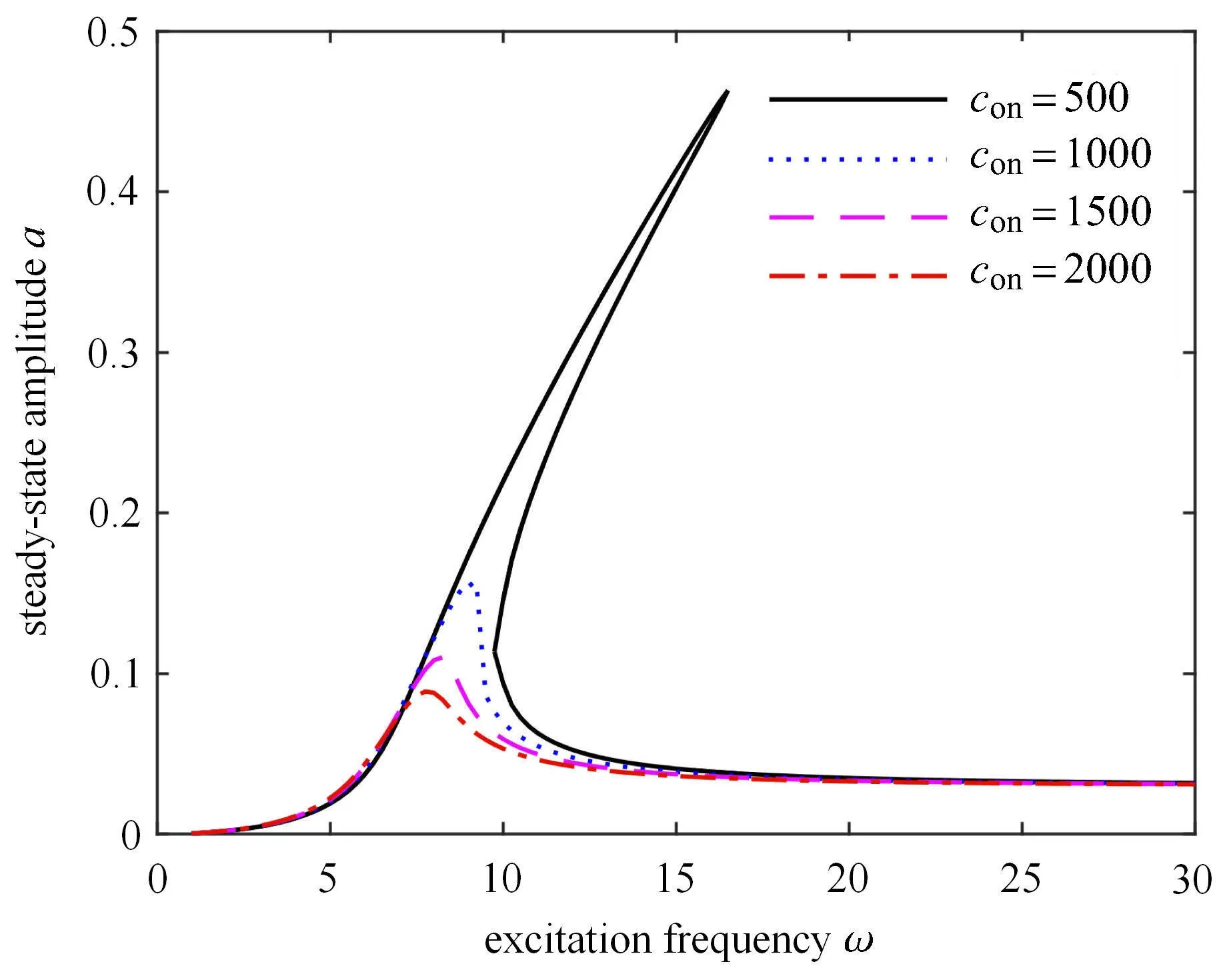
图5 con 变化时的幅频响应曲线Fig.5 Amplitude-frequency responses with different con
令con=1000 N·s/m 且保持不变,coff分别取50,200,500 和1000 N·s/m 时系统的幅频响应曲线如图6 所示.从图6 可以看出,随着coff增大,在低频域系统的共振振幅逐渐减小,而在高频域内系统的共振振幅逐渐增大,式(33)也表明,幅值a除与阻尼有关外,也与外激励频率ω 有关.
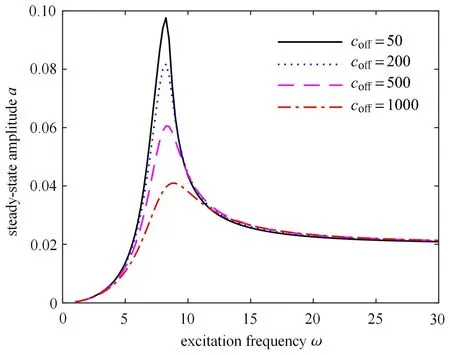
图6 coff 变化时的幅频响应曲线Fig.6 Amplitude-frequency responses with different coff
4.2 外激励振幅的变化分析
以ADD 控制为例,半主动开关控制的开/关阻尼保持不变,取con=2000 N·s/m,coff=0.02con,分析外激励幅值A变化时对主共振振幅的影响.A分别取0.01,0.03,0.05 和0.08 m 时系统的幅频响应曲线如图7 所示.从图7 中可以看出,外激励幅值A越大,系统的共振振幅越大.

图7 外激励振幅变化时的幅频响应曲线Fig.7 Amplitude-frequency responses with different A
4.3 3 种控制策略的控制效果分析
这里分析3 种半主动控制策略对于同一个悬架系统的控制效果,并与未加控制的悬架系统进行比较.外激励振幅A=0.04 m,开关控制阻尼分别为con=1500 N·s/m,coff=0.02con,得到3 种控制策略下系统解析解的幅频响应曲线和未加半主动控制时系统解析解的幅频响应曲线,如图8 所示.从图中看出,3 种控制策略下系统的共振响应振幅与未加半主动控制时相比均有明显的降低:在低频时,基于速度--相对速度反馈的SH 控制策略在降低振幅方面最优,减振效果最好;在高频时,基于加速度--相对速度反馈的ADD 控制策略在降低振幅方面最优.ADD 控制策略在降低共振峰值的同时,共振的频率也发生了偏移.由此可见,采用控制策略改变了幅频曲线的弯曲程度,即改变了系统的频率特性,对共振振幅、定常解的多值性以及系统的稳定性均有影响.
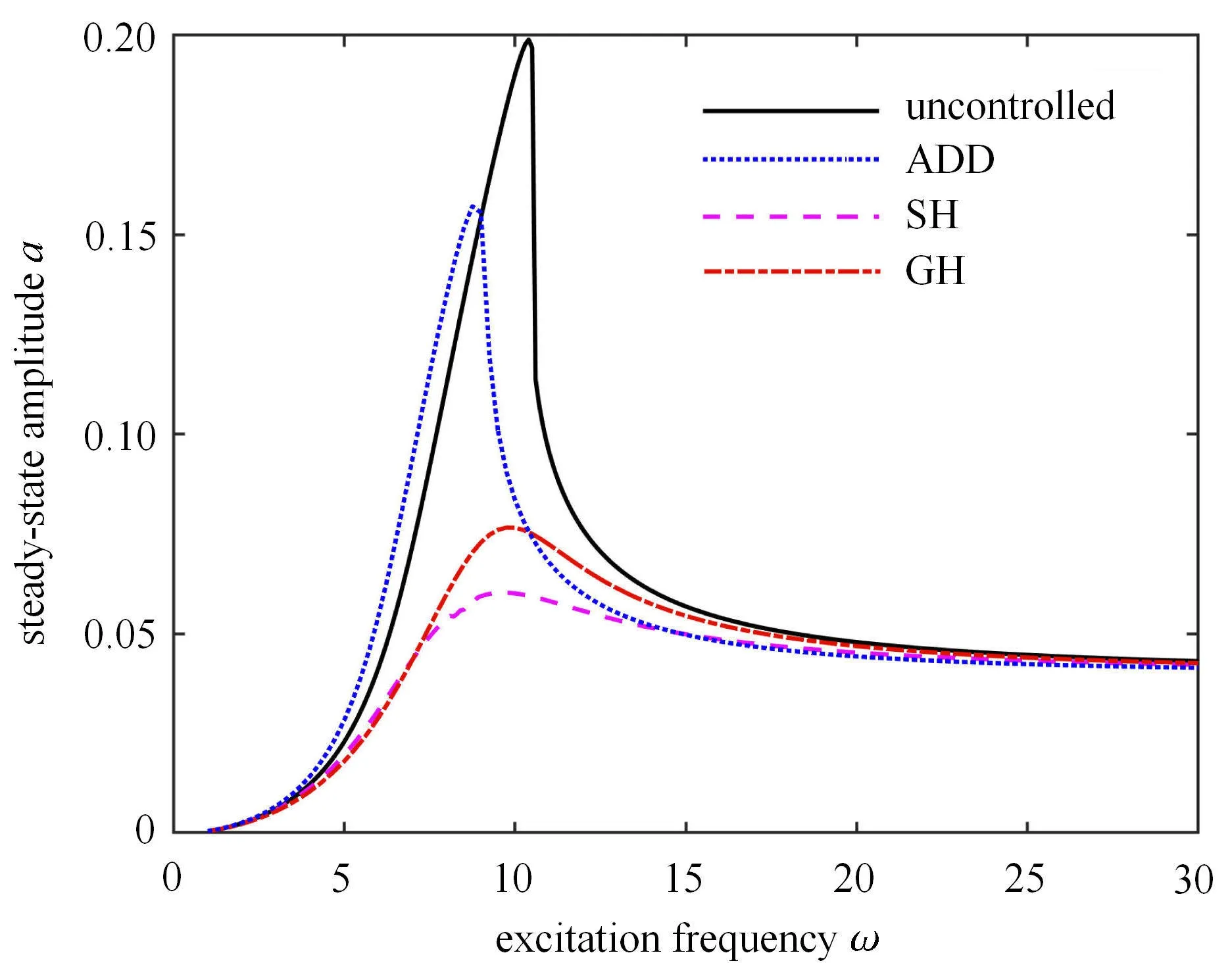
图8 不同控制策略下的幅频响应曲线Fig.8 Amplitude-frequency responses with different control approaches
对比主共振频率附近ω=10 rad/s 时的时域响应,图9 ∼图11 依次为簧载质量的位移时间历程、加速度时间历程以及速度--位移相平面图.从图9 中可以得出与图8 相同的结论,即采用半主动控制策略可明显降低系统的相对位移响应振幅.在主共振频率附近,基于速度--相对速度反馈的SH 控制策略的减振效果最优,均优于基于加速度--相对速度反馈的ADD 控制策略和基于位移--相对速度反馈的GH 控制策略.从图10 中可以看出,采用半主动控制策略在降低垂直加速度的幅值上具有明显的效果.此外,半主动控制策略下的加速度响应存在明显的突变,这是半主动开关控制的分段线性导致的系统强非线性引起的,这也是开关控制的本质特征,在切换过程中会产生的抖振现象,突变的强度依次为ADD 控制策略、SH 控制策略、GH 控制策略.从图11 相平面图中可以看出,采用半主动控制同时能够降低簧载质量振动的位移和速度,而且SH 控制策略的效果最佳.
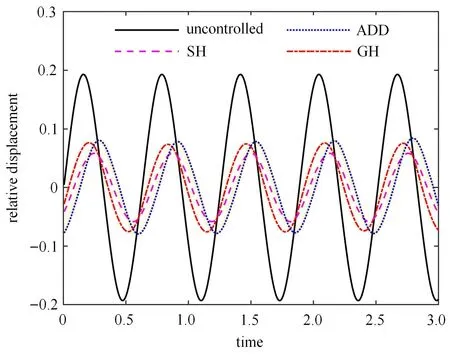
图9 簧载质量的位移时间历程Fig.9 Time history of relative displacement
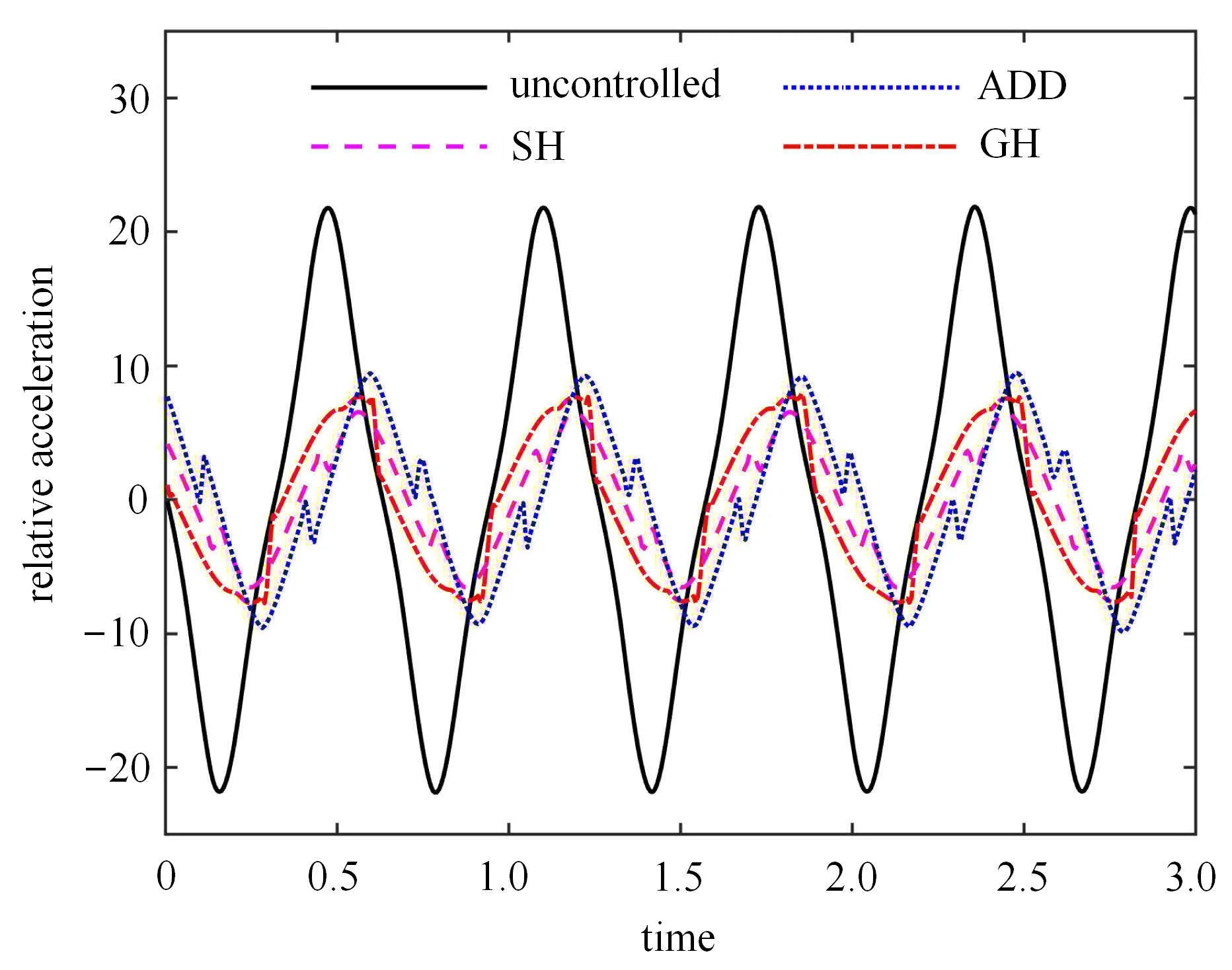
图10 簧载质量的加速度时间历程Fig.10 Time history of relative acceleration
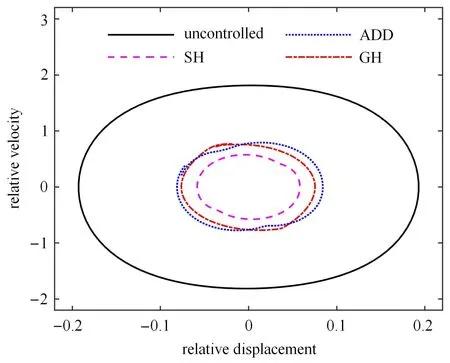
图11 簧载质量的相平面图Fig.11 Phase-portrait of sprung mass
5 随机激励下的控制效果
在实际的工程应用中,非线性隔振系统较多情况下所受到的外力更接近于随机激励,半主动隔振系统在随机激励下的响应更具有实际意义[34-39].采用刘献栋等[40]的数值模拟方法建立D 级路面不平度值来模拟随机激励,如图12 所示.选取车速为10 m/s 情况下时,时间间隔为0.01 s 的40 s 随机激励,得到3 种控制策略下和未加半主动控制时的位移时间历程曲线分别如图13(a)∼图13(d) 所示.
采用车身基于路面的相对位移量的均方根值和加权加速度均方根值对平顺性进行评价[41],按下式计算加权加速度均方根值
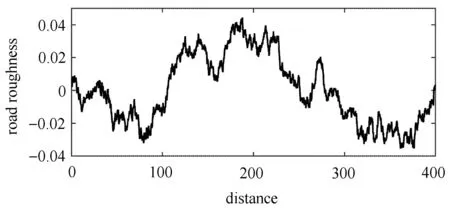
图12 D 级路面的不平度Fig.12 Road roughness of D grade

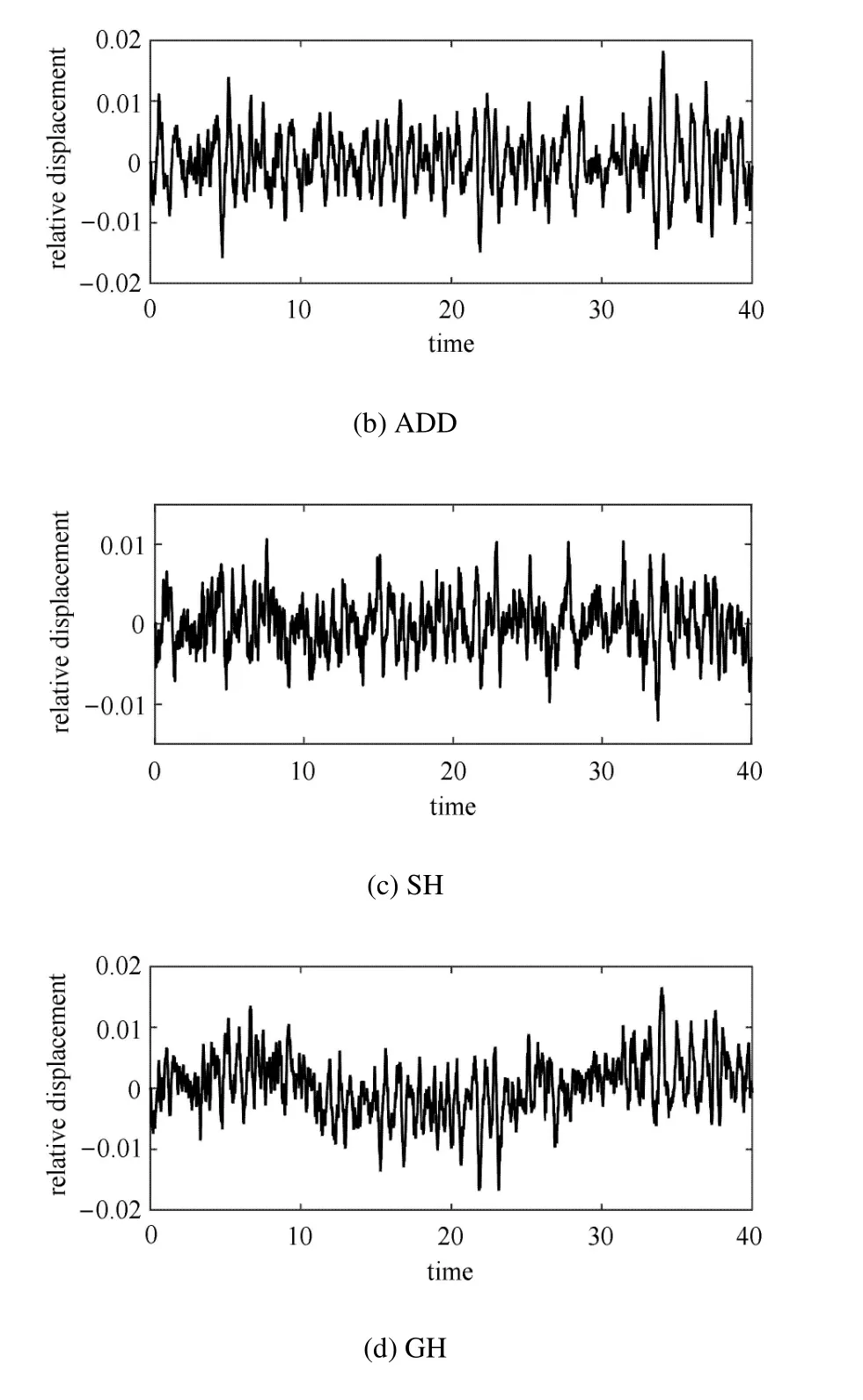
图13 不同控制策略下相对位移的时间历程曲线Fig.13 Time history of stochastic relative displacement responses

式中,T为振动的分析时间.
不同控制策略下位移均方根值和加权加速度均方根值的结果如表1 所示.由图13 和表1 中可以看出,相对于未加控制策略来说,3 种控制策略都能够有效降低系统的相对位移量和加权加速度均方根值,提升平顺性效果明显.基于速度--相对速度反馈的SH 控制策略在降低相对位移量方面更突出,而基于加速度--相对速度反馈的ADD 控制策略更侧重于降低加权加速度均方根值.
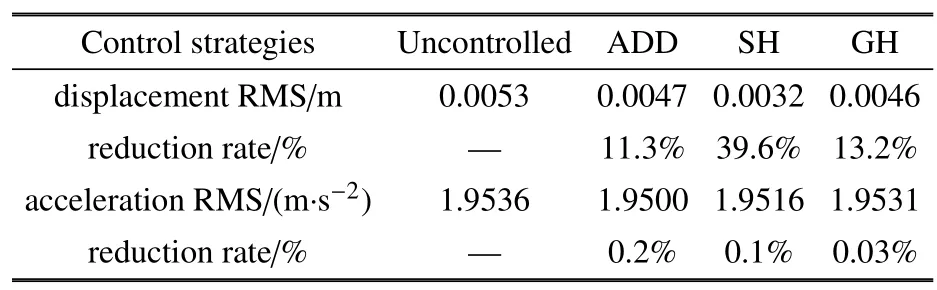
表1 不同控制策略下性能指标均方根值Table 1 RMS values of relative displacement and acceleration
6 结论
本文对一类基于相对速度反馈控制的半主动隔振系统的解析求解以及动力学行为进行了研究.首先利用平均法求解了未加控制时含立方刚度的单自由度隔振系统在主共振情况下的响应,进而分别采用加速度--相对速度反馈的ADD 控制策略、速度--相对速度反馈的SH 控制策略和位移--相对速度反馈的GH 控制策略对系统的一阶近似解进行了分析,利用Lyapunov 理论分析了系统的稳定性,得到了系统定常解的稳定条件.利用数值仿真对一阶近似解进行了验证,结果表明解析研究结果和数值解具有很好的一致性.最后对3 种控制策略分别在简谐激励和随机激励下的控制效果进行了对比分析,分析结果表明,在抑制共振响应振幅方面,低频时SH控制策略的减振效果最好;高频时ADD 控制策略的减振效果最优.ADD 控制策略在降低加权加速度均方根值方面更为突出,可以有效提升平顺性.本文提供的半主动控制隔振系统的解析研究,也可应用到其他半主动开关控制策略中,为半主动隔振系统的控制策略研究提供了参考.

