随机空间柔性多体系统动力学分析1)
郭祥 靳艳飞 田强
(北京理工大学宇航学院,北京 100081)
引言
随着高新技术的发展,在实际工程技术中,特别是轻质、高精度、柔性零部件被广泛应用于众多工程领域,如空间站柔性操作机械臂、卫星环形桁架天线、航天器太阳帆板、空间机器人等.因此,系统各部件以刚体为假设的多刚体系统动力学不再适用当前的研究需求.传统的柔性多体系统动力学特性的描述方法存在着众多缺点,且某些动力学模型本身就不精确.在小转动和小变形假设下的公式无法精确描述多体系统柔性部件同时承受大转动和大变形的情形[1-2].Shabana[3]提出了绝对节点坐标法(absolute nodal coordinate formulation,ANCF) 对具有大整体运动和大变形的柔性多体系统精确地建模.ANCF 作为一种精确的非增量有限元方法,已成为柔性多体系统研究的奠基石[4-7].
然而在传统的多体系统研究中,系统的参数一般被认为是确定性的或可精确测量的.而在实际工程中,由于设计公差、装配制造误差、环境温度、摩擦、磨损等因素的存在,导致系统的材料特性、动力学参数、载荷、边界条件、初始条件等都具有不确定性,最终导致系统的刚度、质量和阻尼特性也具有不确定性.研究表明,若将把某些不确定量假定为某一确定性量,是对真实模型的过度简化,甚至会得出矛盾、不合理的分析结果[8].Wu 等[9]将几何参数和外力均考虑为不确定性参数,研究了不确定性参数对曲柄滑块机构的位移影响.赵宽等[10]研究了不确定性参数对旋转杆滑块系统动力学响应的影响.上述研究仅限于不确定性多刚体系统动力学,具有不确定参数的柔性多体系统的动力学研究还面临众多挑战.
工程系统建模中广泛使用的不确定性表示方法包括区间数学、模糊理论和概率分析.区间数学不需要关于参数不确定类型的信息,区间分析的目的是根据模型输入和参数的边界估计不同模型输出的边界[11-15].研究表明,区间理论分析结果较为粗糙,某些情况下会带来较大误差[16].模糊理论中模糊集的表示是用隶属度函数来刻画的,利用模糊算法可以计算出一个模型输出在另一个集合中的隶属度[17-19].模糊理论在描述模糊概率判断的隶属度函数时,显得过于武断和不够精确[16].描述物理系统不确定性最广泛使用的方法就是概率分析.基于经验积累,工程中大部分不确定性因素均可用特定的概率分布描述,且各个不确定性因素都存在其相应的物理意义.概率分析方法可以描述由随机扰动、变异性条件等引起的不确定性,且其输出的统计特性是由随机输入模型的概率分布来估计的[20].
通常不确定性分析的最终目的是统计矩和可靠性的估算.由计算表达式不难知道,数学上的统计矩和失效概率的估算其实就是求积分.一般情形下,对于实际工程问题的积分式都不存在封闭解,不确定性分析的本质内容就是求解其近似解.数字模拟法(抽样法)是不确定性分析中较早发展且相对简单的方法,其主要包括蒙特卡洛法[21]、重要性抽样[22]、分层抽样[23]、拉丁超立方抽样[24]和自适应抽样[25]等.局部展开法主要用来估算可靠性,主要包括一次二阶矩法[26]、一次可靠度法[27]和二次可靠度法[28]等.不确定性分析也可以通过数值积分的方式得到.数值积分法主要用于估算统计矩,主要包括全因子数值积分法[29]、单变元降维法[30]、基于稀疏网格数值积分法[31]、随机因子法[10]等.以上几种不确定性分析方法,功能较为单一,只能用于估算统计矩或估算失效概率.
随机展开法是不确定性分析中一种较为经典的方法,主要包括随机配点法[32]和混沌多项式展开法(polynomial chaos expansions,PCE)[33-34].其中,PCE 方法最大的优势在于其能够精确地描述任意分布形式的随机变量,并能构建原随机输出变量的代理模型,可以得到原输出量的任意不确定性信息,如统计矩、可靠性、概率密度函数等,同样也适用于稳健性设计和可靠性设计.PCE 方法大致分为侵入式混沌多项式展开(intrusive polynomial chaos expansion,IPCE)[35]和非侵入式混沌多项式展开(non-intrusive polynomial chaos expansion,NIPCE)[36].Sandu 等[37-38]利用IPCE方法对不确定性多刚体系统响应进行分析,但是对于原模型方程较为复杂时,例如原模型的广义坐标数目或随机输入参数较多的情况,对原模型方程进行诸多改动和变换非常不便,故此种方法不再适用;而NIPCE 不需要对原模型方程进行改动,将响应函数看作“黑箱子”,仅关注输入与输出随机变量之间的函数映射关系即可.因此NIPCE 被广泛用来分析不确定性动力学问题,且在实际工程问题中的应用更为广泛.
对于PCE 方法,获取PCE 系数是最关键的一步,关系着PCE 模型的效率和精度.对于非侵入式混沌多项式展开法,可以采用Galerkin 投影的方法[39-40]或随机响应面法(stochastic response surface method,SRSM)[41]对工程系统进行不确定性分析.基于Galerkin 投影的PCE 方法在构建PCE 模型时,构建过程以及PCE 模型的形式与SRSM 是完全一样的,唯一不同的地方在于估算PCE 系数的方法不同.Galerkin 投影的方法利用Galerkin 投影来获取PCE系数,而SRSM 则是运用回归方法.
Isukapalli[41]提出的高效配点法(efficient collocation method,ECM) 的优点是利用高概率区域的点较好地捕获模型的行为.由于配点的选择与多项式混沌展开的项相对应,从而避免了未知系数的线性方程组的奇异性.但是正如Atkinson[42]所述,ECM 方法不能收敛于三阶多项式混沌逼近,这是由于配点方法的内在不稳定性造成的.特别是对于高阶多项式近似,因为要求多项式(曲线或曲面) 必须通过所有的配点,而在实际计算过程中只选择了其中部分配点,具有一定的主观性,因此这种配点方法在本质上是不稳定的.靳红玲[43]利用改进抽样的回归方法(regression method with improved sampling,RMIS)分析了随机平面柔性梁系统动力学响应;皮霆等[44]也利用该方法对不确定性刚柔耦合曲柄滑块机构进行了分析,该回归方法的计算成本虽高,但其不失为一种较为稳健的估计函数逼近系数的方法.因为在该方法中使用了更多样本点的模型结果,并且每个样本点对模型的影响由所有其他样本点调节.但是由于该抽样方法得到的样本组合数呈指数增长,计算过程中不可能将所有样本点全部进行回归运算,目前仅局限于选取其中部分样本(一般取N=2K组,K为混沌多项式展开项数),存在太多主观因素,使得计算结果的精度受到影响.单项求容积法则[45](monomial cubature rules,MCR) 所产生的回归样本点组合数相对较少,且将多元积分近似为被积函数在若干离散积分节点上的函数响应值的加权和,得到具有较高代数精度的积分形式.
本工作采用ANCF 来描述含多个随机参数的空间柔性多体系统,基于广义alpha 算法提出了一种非侵入式的混沌多项式计算方法来求解随机微分−代数方程组.同时对比了当前几种统计矩估算方法的计算效率,得出采用MCR 方法确定的样本点组数相对较少,从而提高了计算效率.此外通过数值算例发现,随机参数对空间柔性多体系统动力学响应的影响是不可忽视的.本工作以期为分析随机柔性多体系统的动力学行为提供参考.
1 含随机参数的柔性多体系统
本文采用ANCF 描述缩减三维曲梁单元的变形[46],利用相关动力学原理可得到系统动力学的微分代数方程
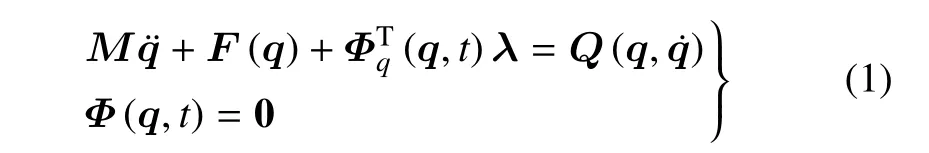
其中,M为系统广义质量阵,q为系统广义坐标,Q为系统广义外力,F为系统广义弹性力,Φ和Φq分别为系统约束方程以及对广义坐标的Jacobi 矩阵,λ为Lagrange 乘子.
系统中第i个单元的质量阵可表示为
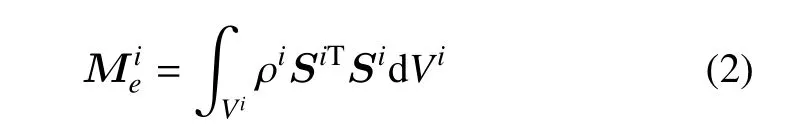
利用ANCF 建模得到的系统质量矩阵为常数矩阵.由虚功原理
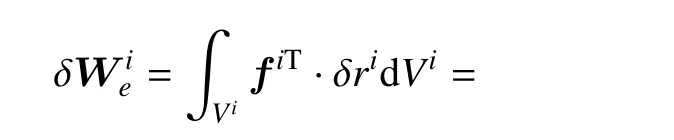
可得到系统广义外力为

文献[46] 根据虚功原理并采用第一类Pioa-Kirchhoff 应力张量的方法推导得到弹性力F及其Jacobi 矩阵的解析表达式可使基于ANCF 建模的计算效率大大提高.
根据方程(1),可将含随机参数的柔性多体系统动力学方程可表示为
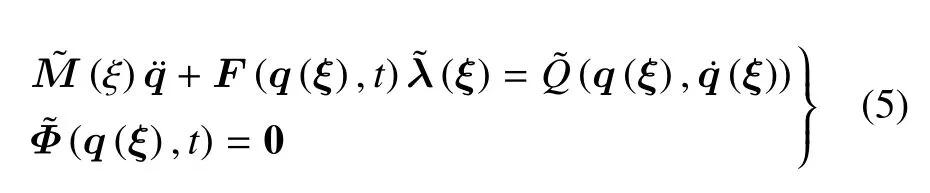
其中,带“∼” 的矩阵和向量均为含有随机参数的矩阵和向量,随机变量ξ=[ξ1,ξ2,···,ξd],第i个随机参数可表为ξi(i=1,2,···,d) 的函数,d为随机参数个数.
2 非侵入式混沌多项式计算方法
针对随机微分−代数方程组(5),本节介绍一种非侵入式混沌多项式计算方法.
2.1 混沌多项式展开
设随机过程Y可利用混沌多项式[16]表为
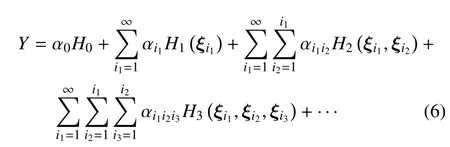
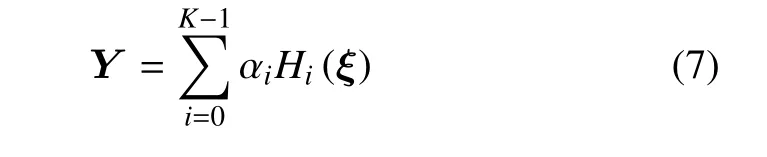
其中,Hi(ξ) 为p阶 Hermite 正交多项式,ξ=[ξ1,ξ2,···,ξd],αi为待定系数.Y的展开项数

其中,d为输入随机变量维数,p为混沌多项式展开的阶数.阶数越高截断误差越小,展开项数越多.结合实际计算情况,一般取p=2 或p=3 时的PCE 模型即可得到较为精确的结果.
2.2 随机系统动力响应分析
2.2.1 随机响应面法
将系统的输入输出变量全部用混沌多项式展开之后,为求得系统输出响应的统计矩信息,需要得到待定系数的信息.对于非侵入式混沌多项式的不确定性分析方法,最常用的方法就是随机响应面法[16],图1 为随机响应面法的计算流程图.随机响应面法主要包括抽样、随机响应面的构建.
Step 1随机响应面的构建.
设y=f(x)的输出响应的p阶混沌多项式展开为
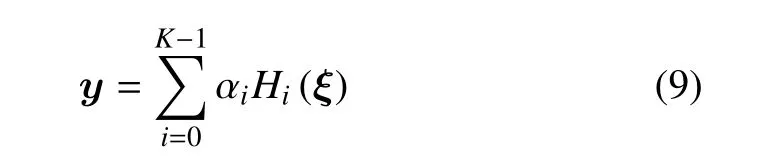
其中,ξ为d维标准随机变量,一般情况d与随机输入变量x的维数的相同,αi是待定的PCE 系数.
Step 2估算PCE 模型中的系数.


图1 随机响应面法流程图Fig.1 Flow chart of SRSM

根据线性最小二次回归可得
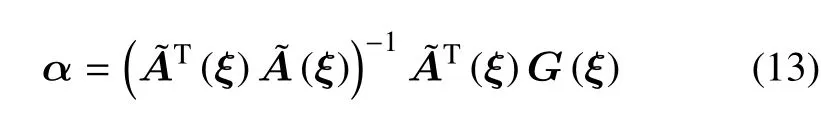
2.2.2 单项求容积法则
关于随机响应面法Step 2 中样本点的选取,另一种有效的方法是单项求容积法则[45].运用MCR获得回归的样本点的优势在于:可以运用较少的积分点数得到较高代数精度的积分形式,且由MCR 产生的样本点可以全部用来估算PCE 系数,保证了不确定性传播的精度.适用于具有5 阶精度d(d3)维变量的MCR 公式为

式 (14) 中求和号下面的 “permutation” 意为对括号中的数做全排列,式(14) 中第一项排列结果为(r,0,···,0),(0,r,0,···,0),···,(0,···,0,r),(−r,0,···,0),(0,−r,0,···,0),···,(0,···,0,−r),第二项同样对±s作全排列,A,B,C,D为常数.本文在求解PCE 系数时只需对公式中给出的样本点进行回归计算,总的样本点组数为N1=2d+2d.虽然式(14)的样本点组数比文献[43]中的公式I 增加较多,但对于较高维变量的问题具有较好的计算稳定性.
适用于具有7 阶精度d(d=3,4,6,7) 维变量的MCR 公式为

积分点个数为N2=2d+2d2+1.
2.2.3 随机输出响应变量的数字特征
利用随机响应面法得到PCE 的系数之后,可以较为方便的得出随机输出响应变量的数字特征

2.3 非侵入式随机微分代数方程组计算方法
将方程组(5) 通过差分直接离散成随机代数方程组进行求解,迭代过程如下
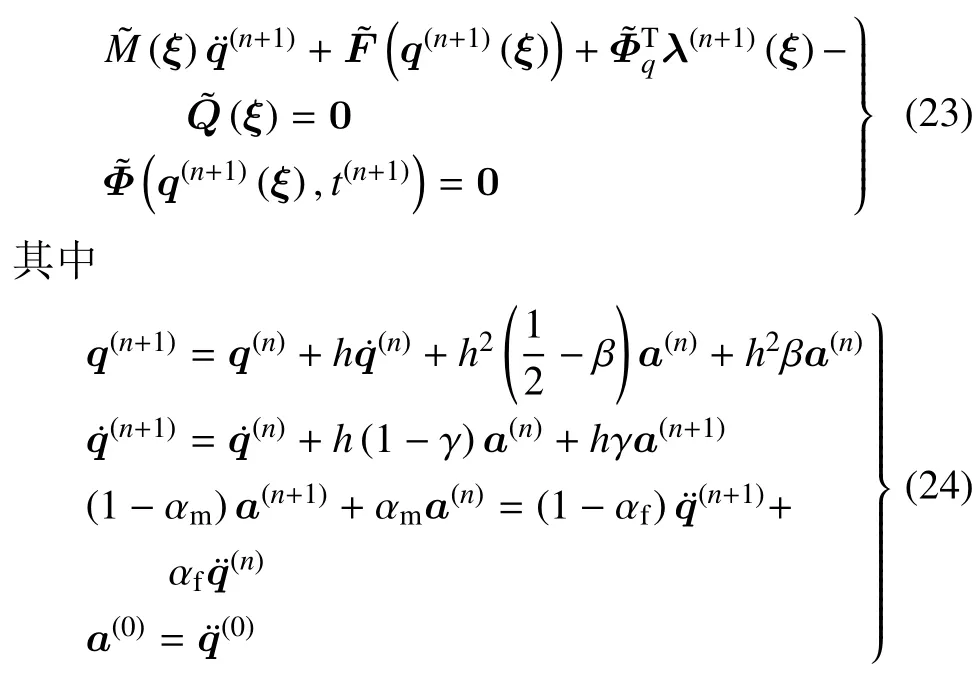
广义alpha 算法的参数取值为
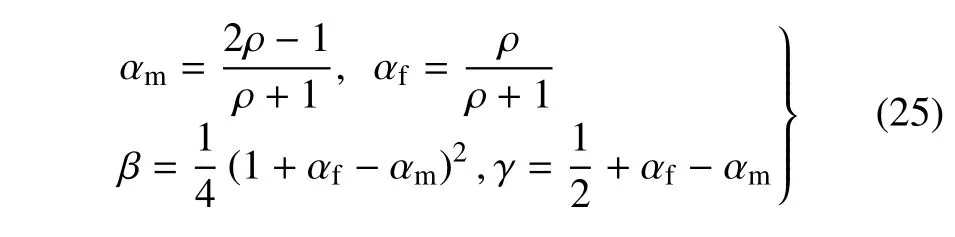
其中,算法谱半径ρ ∈[0,1],ρ 取值越大耗散越小,本文取ρ=0.8.设方程组(5)的解为
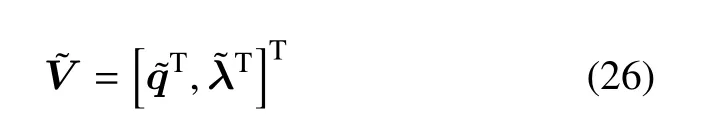
其中,,分别为随机广义坐标以及随机拉格朗日乘子,定义在第n个时间步长上的非线性方程组为
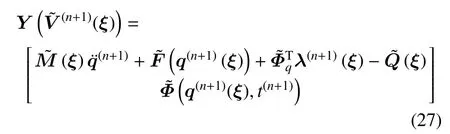
非线性方程组(27)可由Newton-Raphson 迭代求解

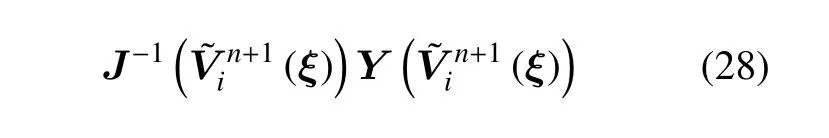
式中i表示第i次Newton-Raphson 迭代,J为Y关于V的Jacobian 矩阵
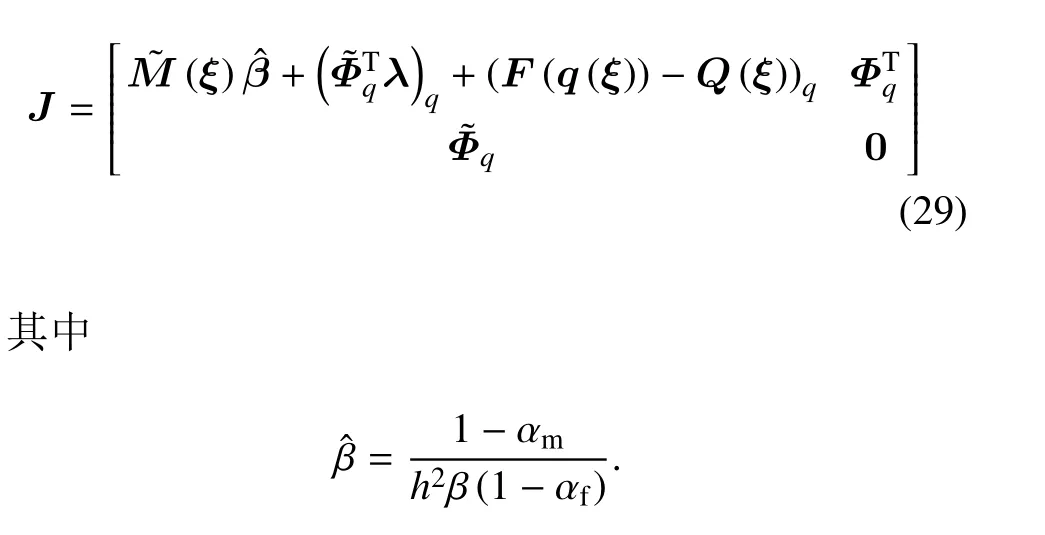

图2 非侵入式随机微分代数方程组求解算法Fig.2 The non-intrusive computation methodology for solving stochastic DAEs
本文提出的求解随机微分代数方程组的非侵入式计算方法流程图如图2 所示,首先针对系统中所含的随机参数选取N组样本点,样本点组数N由具体的采样方法、PCE 阶数及随机变量维数确定;其次,随机响应面法与广义alpha 算法相结合,将SDAEs 转化为若干组确定性非线性代数方程组.图2中样本点简写为 ξ=简写为ξj,j=1,2,···N.ξj为具体某一组采样的样本点,tol为Newton-Raphson 迭代过程中的收敛误差,Tfin,h分别为总仿真时长和时间步长.得到PCE 的系数后,根据式(21)和式(22)可计算输出响应的均值和标准差.
3 数值算例
如图3 所示,空间六连杆柔性多体系统的各杆长度分别为l1=l2=l3=l4=l5=2 m,l6=4 m,密度和杨氏模量分别为ρ=2767 kg/m3,E=6.895×1010Pa.本文对空间六连杆柔性多体系统分别使用含4,4,4,4,4,8 个ANCF 缩减梁单元对各杆进行建模.为了获得更加精确的结果,避免所采用的ANCF单元产生泊松闭锁问题[48-49],本文不考虑梁单元的泊松效应,假定泊松比为零.梁的截面积和惯性矩分别为A=7.299×10−5m2,I=8.215×10−9m4.设重力加速度g=9.81 m/s2,初始状态为水平,考察系统在重力作用下的动态过程.现设空间六连杆柔性多体系统的密度、杨氏模量、截面积和转动惯量为服从正态分布的随机变量,即=ρ+r1ρξ1,=E+r2Eξ2,=A+r3Aξ3,=I+r4Iξ4,ri(i=1,2,3,4)为不确定性系数.此外,所使用的计算机主要参数为8 核主频2.3 GHz 的CPU 和8 GB 内存,本文算例的仿真时间步长均为5×10−4s.
图4 给出了不确定性系数ri=0.05(i=1,2,3,4)时的运动过程,基于混沌多项式的随机响应面法,分别采用改进抽样的回归方法(RMIS)及单项求容积法则(MCR)所选取的样本点计算随机空间六连杆柔性多体系统末端点B6的X方向和Z方向位移响应的均值和标准差.图4(a)和图4(c)分别给出了系统末端点B6的X方向和Z方向位移随机响应的均值;图4(b)和图4(d)为末端点B6的X方向和Z方向位移随机响应的标准差,并分别与蒙特卡洛模拟(MCS)104次的结果对比.由于MCS 计算成本较高,故只对比前2 s 的运动过程,三种方法MCR,RMIS,MCS 的计算时间分别为629.65 s,783.77 s,2.519 3×105s.结果显示MCR 方法所得结果与MCS 方法基本吻合,RMIS 方法在确定样本点时具有一定的主观性,造成其计算结果较为不稳定.
为了进一步研究空间六连杆柔性多体系统在较长时间的运动过程,图5 给出了不确定性系数ri=0.05 (i=1,2,3,4) 时空间六连杆柔性多体系统的末端点的位移随时间变化的历程图,仿真时间为10 s.其中图5(a)和图5(c)分别给出了系统末端点B6的X方向和Z方向位移的确定性模型响应(deterministic model response,DMR)与随机响应的均值,图5(b)和图5(d)为X方向和Z方向随机响应的标准差.随机响应的均值和标准差全都分别用RMIS 和MCR 方法计算得到,且其混沌多项式展开阶数均为p=2,不确定性系数rall=0.05 等价于ri=0.05(i=1,2,3,4).由于RMIS 方法在选择样本点时,不同的样本点组合计算得出的结果都是不相同的,RMIS1 和RMIS2 分别为不同的样本点组合的情况,造成其计算结果不稳定.而MCR 方法所确定的样本点可以全部用于计算过程,其计算结果比RMIS 方法较为稳定.
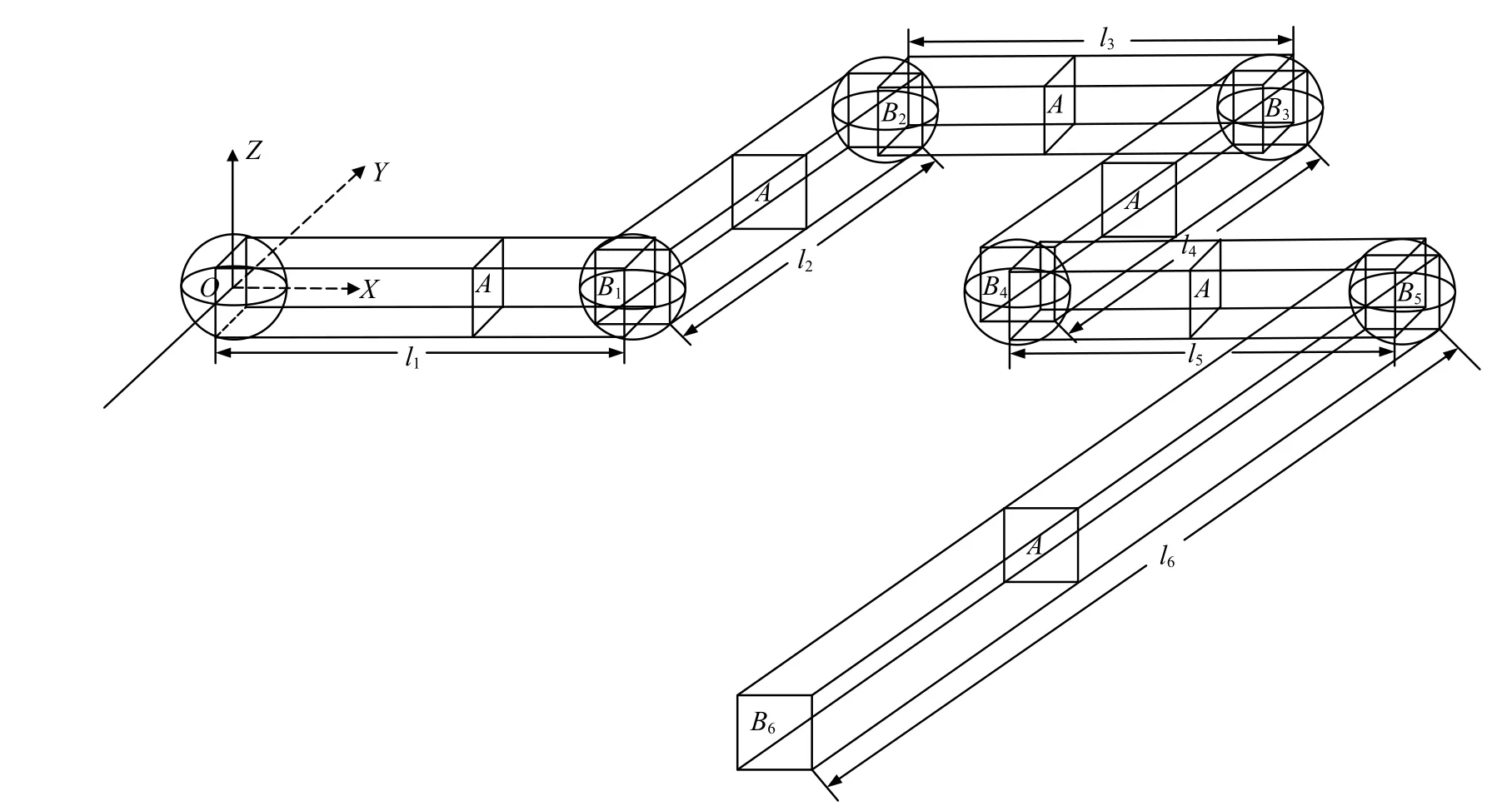
图3 空间六连杆柔性多体系统示意图Fig.3 Schematic view of the spatial flexible multibody system

图4 系统末端点位移响应Fig.4 Displacement response at the end point of the system
此外,RMIS 方法除了计算结果具有不稳定性,其计算效率较MCR 方法也是大打折扣.假设空间六连杆柔性多体系统各杆长度为服从正态分布的随机变量,即li=li+riliξi,i=1,2,···,6,ri为不确定性系数,其余参数取值与上述算例一致.图6(a)和图6(b) 分别给出了系统末端点B6的X方向和Z方向位移的确定性模型响应(deterministic model response,DMR) 与随机响应的均值.其中随机响应的PCE 展开阶数为p=2,不确定性系数rall=0.05 等价于ri=0.05(i=1,2,···,6).表1 给出了当PCE 阶数分别为2 和3 时,随机变量维数分别为4 和6 时,MCR方法、RMIS 方法、SGNI 方法和FFNI 方法分别所需的样本点组数.结果显示:MCR 方法的计算效率相对较高,RMIS 和SGNI 方法次之,FFNI 所需的样本点组数随着PCE 的阶数和随机变量维数的增大呈指数上升.
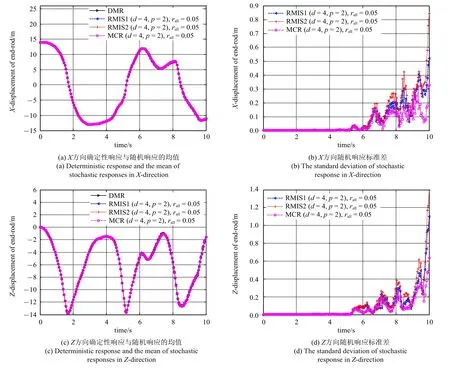
图5 含4 个随机参数的系统末端点位移响应Fig.5 Displacement response at the end point of the system with four random parameters
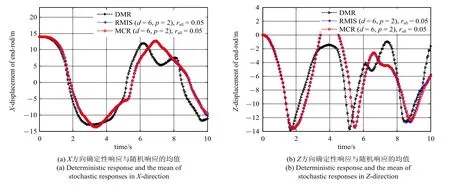
图6 含6 个随机参数的系统末端点位移响应Fig.6 Displacement response at the end point of the system with six random parameters
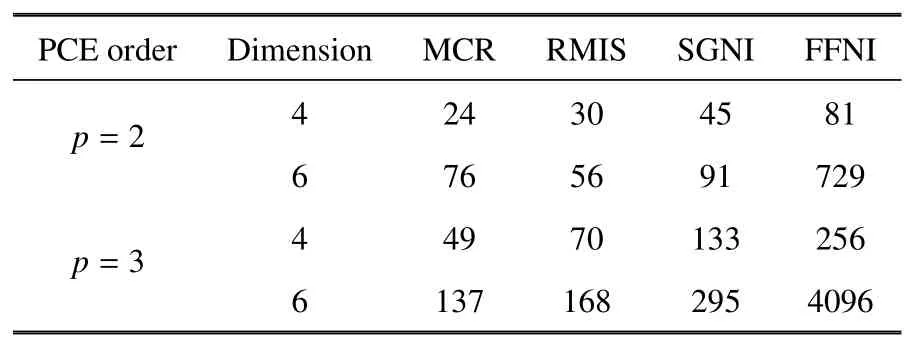
表1 四种方法所需样本点组数Table 1 The number of sample point groups required________________for the four methods
为了深入研究各个随机参数对空间六连杆柔性多体系统动力学响应的影响,图7 ∼图10 分别为d=4,p=3,rall=0.05 时,密度、杨氏模量、截面积及惯性矩的不确定性系数分别为0.05,0.1 时系统末端点X方向和Z方向位移的标准差.当密度、截面积参数的不确定性系数取0.05 时要比0.1 时对随机系统X方向和Z方向位移响应的影响都较为显著;杨氏模量和惯性矩参数的不确定性系数取0.05 时对随机系统X方向位移响应的影响较为显著,取0.1 时对随机系统Z方向位移响应的影响较为显著.
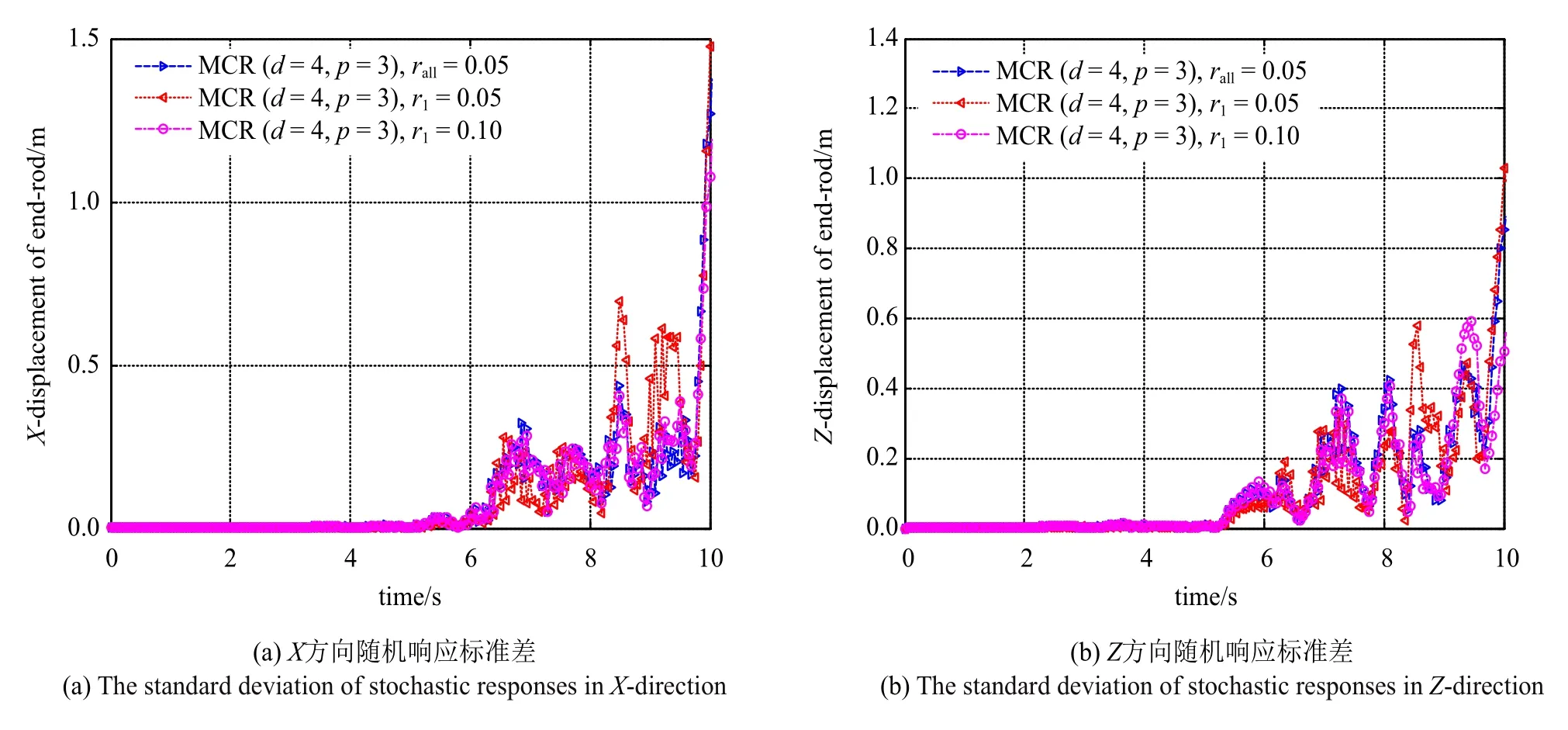
图7 材料密度的不确定性对系统末端点位移响应的影响Fig.7 The influence of the uncertainty of material density on the displacement response of the end point of the system
图8 杨氏模量的不确定性对系统末端点位移响应的影响Fig.8 The influence of the uncertainty of Young’s modulus on the displacement response of the end point of the system
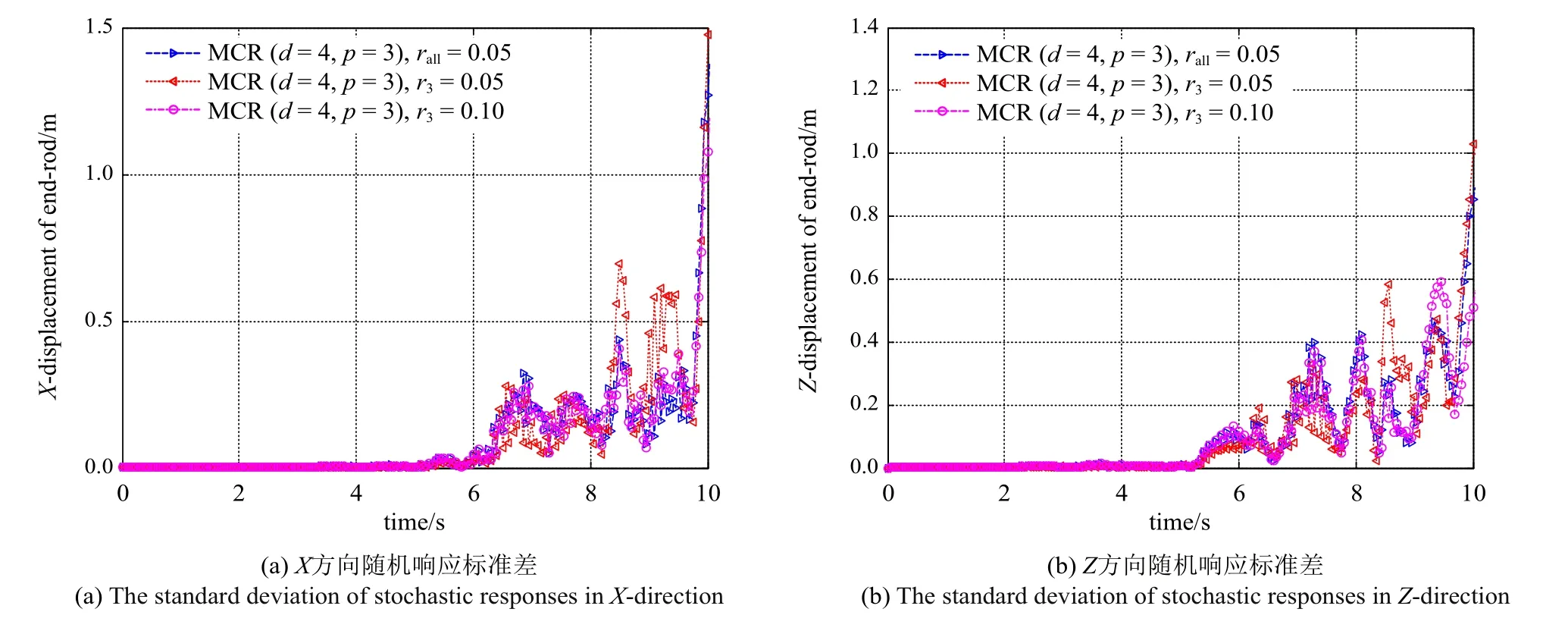
图9 梁截面积的不确定性对系统末端点位移响应的影响Fig.9 The influence of the uncertainty of beam cross-sectional area on the displacement response of the end point of the system

图10 惯性矩的不确定性对系统末端点位移响应的影响Fig.10 The influence of the uncertainty of area moment of inertia on the displacement response of the end point of the system
表2 给出了随机系统前10 s 内,各个参数的不确定性对随机系统响应的数字特征最大绝对值的影响(结果保留4 位小数).结合表2 以及图7 ∼图10可以得出:各个随机参数不确定性对随机系统的均值响应影响较小,但是对随机系统的标准差影响较为显著.其中,杨氏模量和惯性矩的分散性对随机系统X方向位移响应的影响较大; 密度和截面积的分散性对随机系统Z方向位移响应的影响较大.
4 结论
本文针对具有多个随机参数的不确定性柔性多体系统,提出了一种基于广义alpha 算法的非侵入式计算方法.采用ANCF 的缩减梁单元对柔性体进行网格划分.首先利用广义alpha 算法直接将随机微分代数方程组转化为非线性随机代数方程组.然后利用PCE 方法构建系统代理模型,在此基础上采用SRSM 求解PCE 的待定系数.在应用SRSM 方法时分别用RMIS 和MCR 方法进行采样,并用MCS 验证了结果的正确性,同时通过数值仿真得到:与RMIS方法相比,MCR 方法的计算结果更加稳定;且与其他方法相比MCR 方法的计算效率更高.
本文采用MCR 采样策略,对含有随机参数的空间柔性多体系统的动力学行为进行研究.仿真结果表明参数的不确定性对随机系统响应的影响是不可忽视的.数值结果表明,本文提出的计算方法对研究含有多个随机参数的柔性多体系统的动力学特性是有效和适用的.

