浅析复核基桩基础沉降计算分析研究
姚学朝 江苏省有色金属华东地质勘查局
一、引言
桩基础作为一种历史悠久的基础形式,应用非常广泛。桩基设计理论,主要是考虑承载力是否满足要求,也即设计时桩承担绝大部分荷载,如果按照传统的桩基理论来设计,必然会造成用桩总数过多、工程造价过高,差异沉降满足设计要求而总沉降却远低于允许沉降量。
因此复合桩基差异沉降控制优化设计方法出现了,它能利用桩间土承载能力,在满足整体承载力的要求下,可以降低和控制建筑物的沉降。复合基桩由单桩及其对应面积的承台底地基土共同组成,传力路径为上部荷载-承台-桩-桩间土,一方面发挥桩基的优势,减少建筑物沉降;另一方面让桩土协同作用,满足承载力要求,此项设计理念,经济上合理,技术上先进。
二、复合桩基差异沉降计算模型
(一)土体的本构模型
土体采用摩尔~库仑理想弹塑性模型,是较为理想的本构模型。摩尔~库仑强度理论对土的破坏形式做了理想化假定,一般为剪切强度,它与土的粘聚力和法向应力有关,某点在任一平面上剪应力达到此值时,该点处于极限平衡状态,土就发生破坏。
摩尔~库仑模型计算参数共7 个,其中土容重γ、渗透系数k、凝聚力c、内摩擦角φ 可根据现场实测资料来确定它们的值。
杨氏模量E:Plaxis 计算程序使用变形模量E,也可根据压缩模量Es计算E 进行使用:
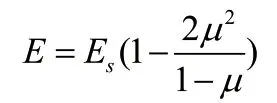
泊松比μ:一般在0.3~0.4 之间,饱和黏土在不排水条件下可能接近0.5。
库仑剪切破坏准则:

式中,
c 为黏聚强度
φ 为内摩擦角
τf为破裂面上的剪应力,也是土的抗剪强度
σ 为破裂面上的法向总应力。
(二)桩和承台的本构模型
由于相对土层来说,桩和承台的刚度大,在正常受力条件下,它们一般处于弹性状态,故假定它为线弹性,线弹性理论模型,在混凝土受力的应力和变形关系中,属于简单本构模型,服从广义胡克定律,两个弹性系数为E 和μ。表达式形式如下:

式中,[D]为应力应变关系矩阵,表达式为:

式中,E、μ 分别为弹性系数。
三、复合桩基差异沉降计算思路
根据多年的研究和经验,可以按照以下思路进行计算:①上部结构对提高建筑物抗弯刚度非常重要,在降低不均匀沉降方面发挥有限。上部结构中,其刚度矩阵元素存在特有性质,因此可以将上部结构的刚度贡献简化到筏板上进行考虑。②在保证桩土共同作用的基础上实现变刚度的调平设计,因此建筑物的沉降将会大于按常规桩基设计时的沉降,土体已经工作于非线性状态。③由于只进行平面分析,将筏板和桩的支承刚度进行换算,使板带的刚度等于筏板的刚度。这样沿板带方向计算出的建筑物不均匀沉降基本反映了建筑物沿该方向的实际变形特性。
四、实例计算
(一)材料参数
桩型采用预制桩,砼强度为C30,桩长30m,桩径为Φ500。计算模型的地下水位取为0m,采用二维轴对称模型来分析,桩与承台简化为线弹性模型,土层简化为摩尔-库仑模型,粘聚力为1kpa,内摩擦角为30 度,泊松比为0.35,荷载按照150kN考虑。
(二)布桩方式
模型1 的布桩方式为:桩数为7 根,均匀布桩,桩间距3.0m;模型2 的布桩方式为:桩数为7 根,中间桩距2.5m,边桩桩距3.0m;模型3 的布桩方式为:桩数为5根,均匀布桩,桩间距2.5m。
(三)土层指标
拟试验场地土层共分为7 层:
②-1 层含水量为39.7%,重度为18.2 kN/m3,孔隙比为1.089,塑性指数为18.6,液性指数为0.79,压缩系数为0.569 Mpa-1,压缩模量为3.68Mpa,粘聚力为18kpa,内摩擦角为14.3 度。
②-2 层含水量为41.4%,重度为17.7 kN/m3,孔隙比为1.172,塑性指数为15.9,液性指数为1.27,压缩系数为0.737Mpa-1,压缩模量为2.99Mpa,粘聚力为16.2kpa,内摩擦角为16.6 度。
②-3 层 含 水 量 为25.2%, 重 度 为19.5kN/m3,孔隙比为0.742,塑性指数为9.27,液性指数为1.01,压缩系数为0.192Mpa-1,压缩模量为10.36Mpa,粘聚力为13.3kpa,内摩擦角为30.0 度。
②-4 层含水量为35.4%,重度为18.0 kN/m3,孔隙比为1.041,塑性指数为13.9,液性指数为1.16,压缩系数为0.578Mpa-1,压缩模量为3.56Mpa,粘聚力为15.1kpa,内摩擦角为20.9 度。
③-1 层含水量为24.0%,重度为19.4 kN/m3,孔隙比为0.726,压缩系数为0.135 Mpa-1,压缩模量为13.44Mpa,粘聚力为11.9kpa,内摩擦角为33.4 度。
③-2 层含水量为23.7%,重度为19.6 kN/m3,孔隙比为0.698,压缩系数为0.128 Mpa-1,压缩模量为14.07Mpa,粘聚力为9.04kpa,内摩擦角为33.6 度。
(四)计算结果分析
本算例针对变桩距模型进行了对比分析,模型1 计算总沉降为94.630mm,差异沉降为6.316mm;模型2 计算总沉降为91.410mm,差异沉降为13.452mm;模型3 计算总沉降为113.100mm,差异沉降为13.022mm;
五、结论与建议
建筑物的平均沉降约为90mm,与计算结果比较吻合,按照变刚度调平的理论方法可以进一步的调平,桩数尚可进一步减少,但是为了满足建筑物的建筑与构造布置,在局部区域桩数不能减少。当然上述区域可以通过缩短桩长的方法来减少桩基的卸荷量,从而达到真正的零差异沉降。

