面向列控系统的多目标测试序列集生成方法

赵晓宇

(中国铁道科学研究院集团有限公司通信信号研究所，北京 100081)

引言

作为典型的安全苛求系统，列控系统融合多种先进技术，用于保证列车运行安全、提高列车运行效率。系统的任何故障都可能会导致不可估量的灾难性后果，为了保证软硬件功能的完整性和正确性，在投入运营之前必须执行严格的系统功能测试。现有的测试技术需要测试人员手动编制测试序列，同时很少根据某种标准对测试序列进行排序，耗时耗力，而且不同厂家的测试手段不同，自动化程度也有不同。赵显琼等[1]提出基于CPN[2]的测试案例和测试序列生成方法；郑伟等[3]提出基于全路径覆盖优化算法和序列优选算法的测试生成方法，而后又提出改进蚁群算法和老鼠迷宫算法[4]；赵晓宇等[5]提出车载设备模式转换测试序列生成方法；但这些均未涉及测试序列的排序问题。

为了尽早发现系统缺陷，并及时反馈给研发人员，测试人员希望通过多个优化原则对测试序列进行排序，执行优先级较高的测试序列。针对持续集成测试问题，何柳柳等[6]改进了强化学习的奖励函数设计和奖励策略。面向测试用例优先排序问题，张娜等[7]在引入3个优先级影响因子的基础上，提出在线调整策略。多目标测试序列优化排序问题可以转化为多目标组合优化问题，一般通过启发式搜索算法寻求最优解集，如粒子群算法、蚁群算法(ACO)和非支配排序遗传算法等。针对高维多目标优化问题，朱占磊等[8]提出线性权重最优支配关系和高维多目标进化优化算法。石宇楠等[9]提出多目标协同进化算法，通过剔除“老年”个体避免算法陷入局部最优。边毅等[10]通过CPU+GPU的并行策略改进适应度评估函数。陈云飞等[11]提出粒子群算法，并研究不同参数的性能影响。相比其他算法而言，ACO具有较优的鲁棒性和并行计算机制。肖箐等[12]讨论ACO在多目标优化问题中的应用。顾慧聪等[13]提出基于ACO的多目标测试用例预优化方法。江君莉等[14]采用直接学习机制避免算法陷入局部最优。邢行等[15]定义基于上位基因段的信息素更新策略。张娜等[16]提出一种动态简约的在线指导蚁群信息更新的多目标测试用例优先级排序方法，避免了蚁群算法的收敛速度缓慢等问题。基于此，本论文在满足测试案例全覆盖的前提下，提出了一种多目标测试序列集生成方法，如图1所示，使得测试人员能够及早发现功能缺陷，提高测试效率。

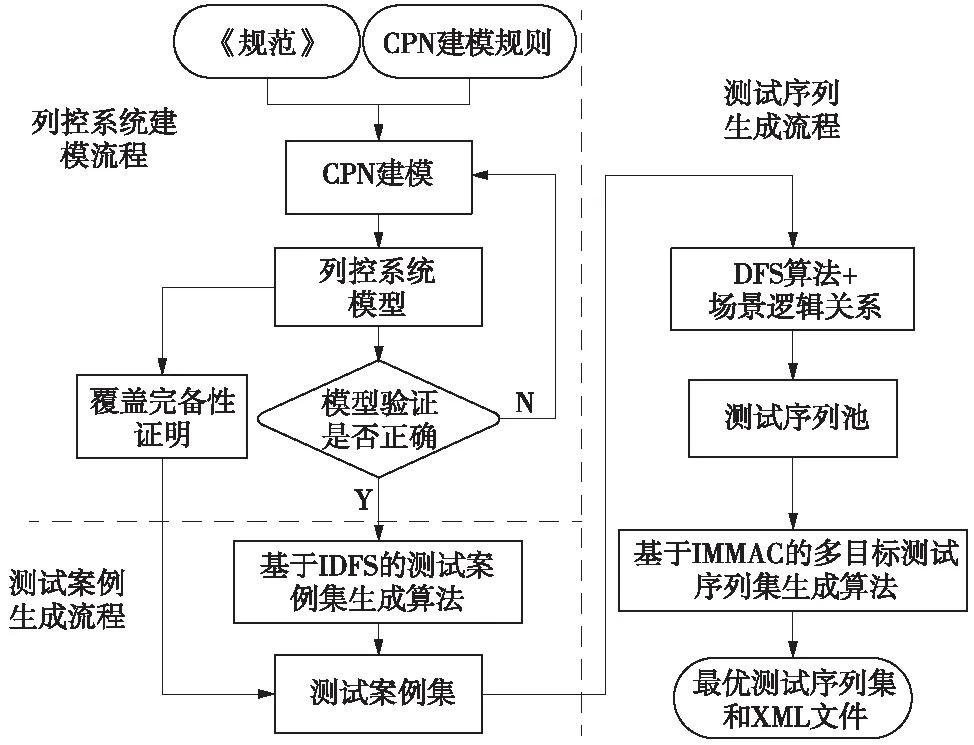
图1 总体框架

1 相关定义

定义1假设蚁群为K:{1，…，AntNum}，测试案例覆盖表为tabuc:{tabuck|k∈K}，测试序列覆盖表为tabus:{tabusk|k∈K}，则测试序列集生成模型PM通过13元素进行描述，即PM={R，C，N，S，Δ(R，C)，Δ(N，C)，Δ(C，S)，Δ(C，tubuc)，Irx，Icy，Isl，Lcy，Lsl}

(1)R:{r1，…，rX}为系统需求集；C:{c1，…，cY}为测试案例集；N:{n1，…，nZ}为模型的状态空间的路径节点集，S:{s1，…，sL}为DFS算法和模型场景逻辑关系生成的测试序列池。

(2)测试需求覆盖矩阵Δ(R，C)，表示C到R的覆盖关系，矩阵元素为

(1)

(3)路径节点覆盖矩阵Δ(N，C)，表示C到N的覆盖关系，矩阵元素为

(2)

(4)测试案例覆盖矩阵Δ(C，S)，表示S到C的覆盖关系，矩阵元素为

(3)

(5)测试案例遍历矩阵Δ(C，tubuc)，表示tabuc到C的覆盖关系，矩阵元素为

(4)

(6)测试需求重要度Irx，根据测试需求的使用情况和复杂程度将Irx分为必用、常用、很少用和几乎不用，取值为1，0.7，0.4和0.1，引发的缺陷等级分别为致命、严重、一般和较轻。

(7)测试案例重要度Icy，表示测试案例覆盖的全部测试需求重要度的总和，由公式(1)可得

(5)

(8)测试序列重要度Isl，表示测试序列覆盖的全部测试案例重要度的总和，由公式(3)和公式(5)可得

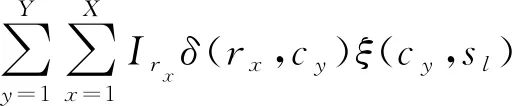
(6)

(9)测试案例路径长度Lcy，表示测试案例覆盖的全部路径节点的总个数，由公式(2)可得

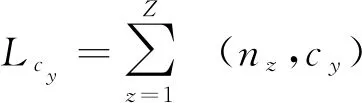
(7)

(10)测试序列路径长度Lsl，表示测试序列覆盖的测试案例路径长度的总和，由公式(3)和公式(7)可得

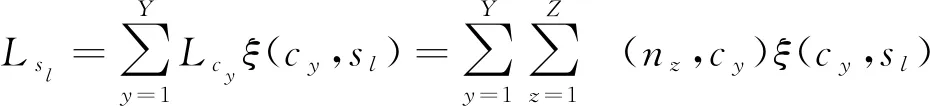
(8)

(9)

2 多目标测试序列集生成方法

2.1 模型的构建及验证

根据TB/T 3530—2018《CTCS-3 级列车运行控制系统系统需求规范》(以下简称“《规范》”)[17]和CPN Tools的建模要求，提出以下建模规则，并采用CPN Tools的ASK-CTL扩展逻辑语言和非标准状态空间查询法对列控系统模型进行分析与验证。

(1)采用分层建模规则构建列控系统模型，顶层模型考虑场景间和场景与接口间的交互关系，中层模型考虑场景的主要功能，底层模型考虑详细功能。

(2)建模流程需严格遵守颜色定义、变量和库所等的命名规则，用于辅助算法实现。

(3)采用ML语言处理全部数据，用于提供算法的输入数据和输出数据。

(4)关于数据内容的判断行为，均在模型的守卫函数中体现。

(5)鉴于列控系统功能复杂性，考虑构建多个模型，用于子系统功能的分析与测试。

2.2 基于IDFS的测试案例集生成算法

为了处理模型的循环(自)回路，在满足路径全覆盖和节点全覆盖的基础上，测试案例集生成算法的描述如下。

步骤1：确定模型状态空间和底层模型集合{M1，…MI}，初始化i=1。

步骤2：针对底层模型Mi，获取邻接矩阵A、开始路径节点ns和结束路径节点ne。

步骤3：根据IDFS算法生成ns至ne的简单路径集(不包括循环(自)回路)，并识别ns和ne间的全部循环(自)回路。删除Mi的全部循环(自)回路，获取邻接矩阵A1；针对每个循环(自)回路顶点，通过Dijkstra算法搜索最短前置路径(ns至回路顶点)和最短后置路径(回路顶点至ne)。针对每条循环(自)回路，补充最短前置路径和最短后置路径，生成包含循环(自)回路的路径集，和简单路径集共同组成Mi的测试案例集Ci。

步骤4：更新i=i+1，如果i≤I，返回步骤2，否则输出测试案例集C:{C1，…，CI}。

2.3 基于IMMAC的多目标测试序列集生成算法

针对包含冗余测试案例的测试序列池，测试人员往往考虑顺序测试，很少根据案例全覆盖和多优化目标对测试序列池进行测试序列的挑选与排序。基于此，将测试序列关注覆盖率、测试序列重要度、测试序列路径长度作为启发式函数，共同作用于蚁群遍历策略，蚁群根据转移概率对测试序列池内的测试序列进行遍历，直至遍历完测试序列池或者满足测试案例全覆盖，而后可得构造解集，采用快速非支配排序法判断构造解的优劣性，通过更新全局最优解集得到最优测试序列集。

2.3.1 多目标测试序列集生成问题

多目标测试序列集生成问题描述为求解满足测试案例全覆盖的部分测试序列的顺序排列。本文提出3个优化目标，即测试序列重要度、测试序列路径长度和平均测试案例覆盖率。

(1)平均测试案例覆盖率。相同覆盖准则的条件下，测试序列的平均测试案例覆盖率越高，测试序列的检错力越强。

(2)测试序列重要度。实际上，经常使用的设备功能需求仅占40%左右[18]，优先执行重要度等级较高的测试序列，能够尽早检测设备功能缺陷，提高测试效率。

(3)测试序列路径长度。测试序列包含的测试路径越长，测试步骤越多，越具有检错潜力。

2.3.2 算法的关键步骤

(1)构造解过程

假设信息素释置于测试序列上，构造解的求解过程即蚁群选择测试序列的过程。蚁群根据转移概率确定下个遍历的测试序列，直至遍历完测试序列池或者满足测试案例全覆盖。

①蚁群初始放置规则。针对测试序列池S:{s1，…，sL}中的全部测试序列，分别对测试序列重要度和测试序列路径长度进行排序，将各序列的前L/2个测试序列存入初始测试序列集Sinit，删除重复序列。约定蚁群初始置于Sinit中的测试序列上，提高算法收敛速度。

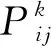
(10)

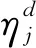
③启发式函数。tabuc覆盖测试序列中测试案例的数量越少，此测试序列对tabuc的贡献越大。顺序遍历对tabuc、测试序列重要度和测试序列路径长度贡献最大的测试序列，能够生成数量最少的测试序列集，即将测试序列重要度、测试序列路径长度和测试序列关注覆盖率作为启发式函数，由公式(6)、公式(8)和式(9)可得

(11)

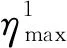
(2)更新信息素

信息素更新策略是为了增加较优解上的信息素浓度，同时降低较劣解上的信息素浓度，从而起到正反馈的作用，引导蚂蚁朝更好的方向进行搜索。

①局部信息素。蚂蚁遍历测试序列后，更新此测试序列上的信息素。局部信息素更新规则如下式所示，ω为局部信息素挥发系数。

τi(t+n)=(1-ω)τi(t)+ωτi(0)

τi(0)=τmax

(12)

②全局信息素。蚁群完成迭代后，更新全局最优解集中的测试序列上的信息素。全局信息素更新策略如下

τi(t+n)=(1-ρ)τi(t)+Δτi(t)

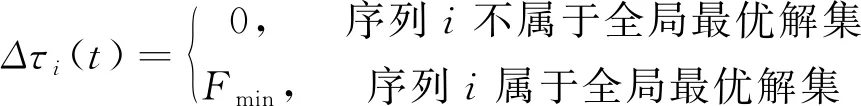
(13)

式中，ρ为全局信息素挥发系数；Fmin=(F1+F2+F3)min为全局最优解集中的最小适应度值。

③信息素阈值。信息素阈值如下

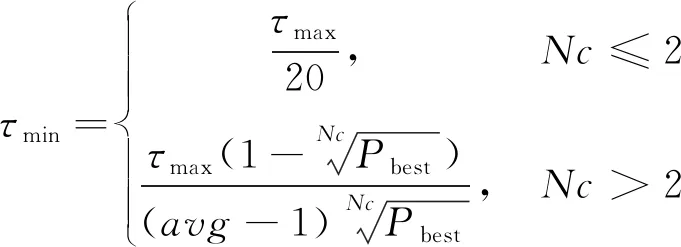
(14)

式中，Nc为迭代次数，avg=Nc/2，Pbest=0.5。

(3)评价解过程

蚁群完成迭代后，根据适应度函数判断构造解集的优劣性。本文根据优化目标设计适应度函数，如下式所示，F1鼓励对平均测试案例覆盖率贡献大的测试序列排在构造解的前面，F2和F3分别鼓励具有更高重要度和更长路径的测试序列排在测试序列集前面

(15)

式中，M1为构造解包含的测试序列数量；Y为测试案例数量；SSy为覆盖测试案例cy的首个测试序列在测试序列集中的位置；h为测试序列sh在测试序列集中的位置；Ish为sh的测试序列重要度；Lsh为sh的测试序列路径长度；C1和C2用于限制适应度函数的值域，此处取C1=10，C2=5。

(4)非支配排序

通过快速非支配排序法判断构造解的优劣性，具体步骤描述如下，dii为种群P中支配个体ii的个体数量，Dii为P中被ii所支配的个体集合。

步骤1：初始化dii，Dii(∀ii∈P)，即令dii=0，Dii=φ。

步骤2：对于jj∈P，如果ii支配jj，则将jj存入Dii，否则dii=dii+1。

步骤3：如果dii=0，将ii加入构造解集。

步骤4：输出最优构造解集。

3 实验及结果分析

3.1 实验设计

根据《规范》和CPN建模规则，对CTCS-3级列控系统的注册与启动、RBC移交和注销场景进行建模。顶层模型如图2所示，包括5个底层模型，即StartProcedure、Train Start-up、Single-RBC HandingOver、Double-RBC HandingOver和EndofMission。状态流运行至Train Start-up模型后，如果ATP与RBC未建立通信，则转至EndofMission模型；如果ATP与RBC已建立通信，当双电台工作时，转至Double-RBC HandingOver模型，否则转移至Single-RBC HandingOver模型。此处仅给出Double-RBC HandingOver模型，如图3所示。

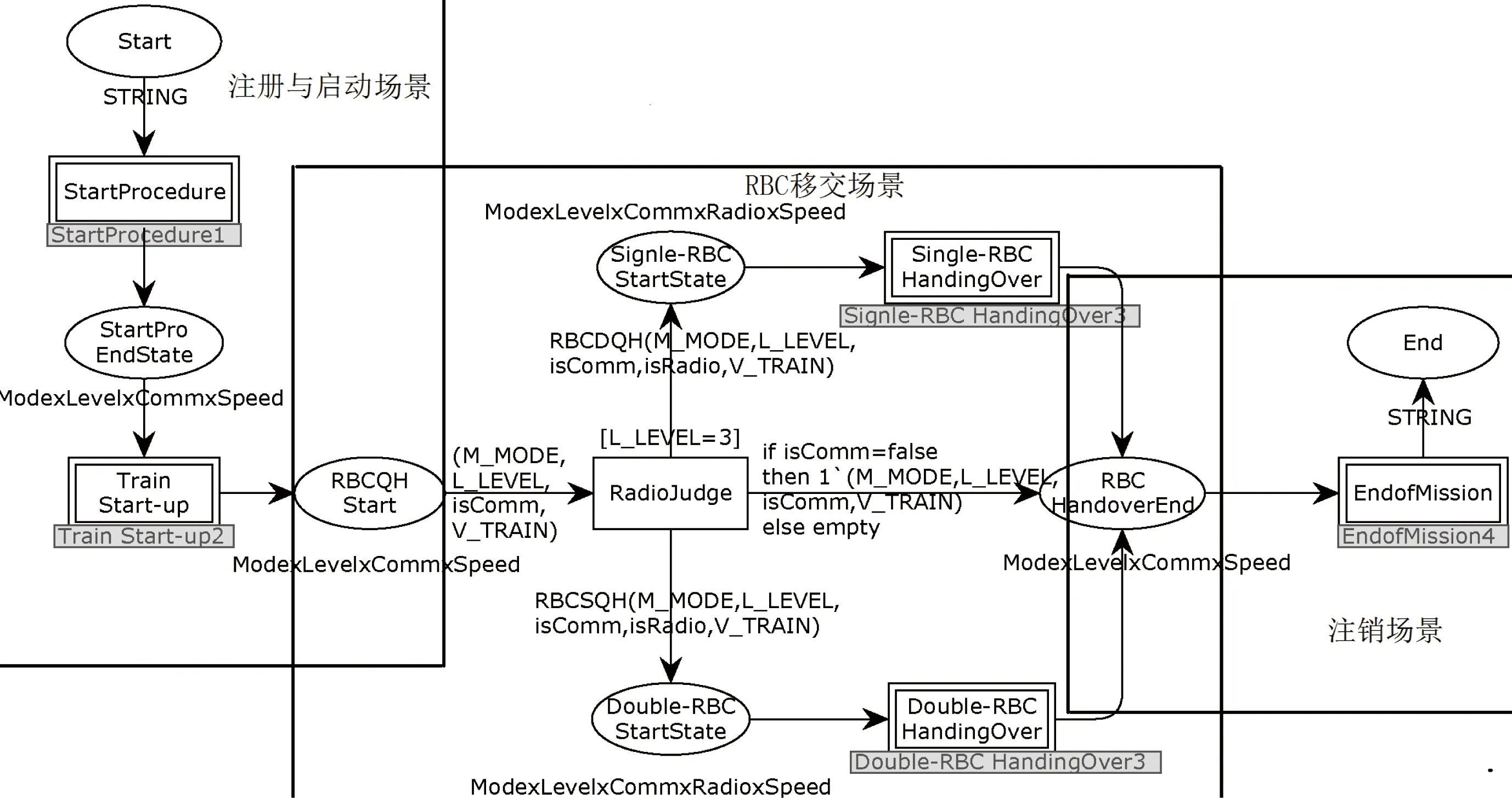
图2 顶层模型

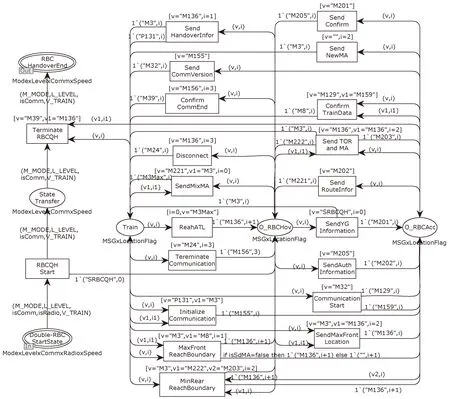
图3 Double-RBC HandingOver模型

运行CPN Tools的状态空间查询功能，得到模型的状态空间，如图4所示。采用测试案例集生成算法生成40个测试案例，得到底层模型及测试案例对应表，如表1所示。通过图4得到测试案例路径长度，根据测试需求重要度的等级划分得到测试案例重要度，如表2所示。参考文献[19-20]，将测试需求重要度划分为必用、常用、很少用和几乎不用，对应数值分别为1，0.7，0.4和0.1。以测试案例c1为例，包含的测试需求有ATP启机、ATP转入SB模式、版本信息错误引起ATP和RBC通信未成功，根据需求使用情况和复杂程度设计重要度数值分别为1，1和0.4，可得测试案例c1的重要度为2.4。本文采用基于IMMAC的多目标测试序列集生成算法生成最优测试序列集，最终通过CPN Tools工具内嵌的XML文件保存功能得到最优测试序列集的XML文件，用于平台测试。

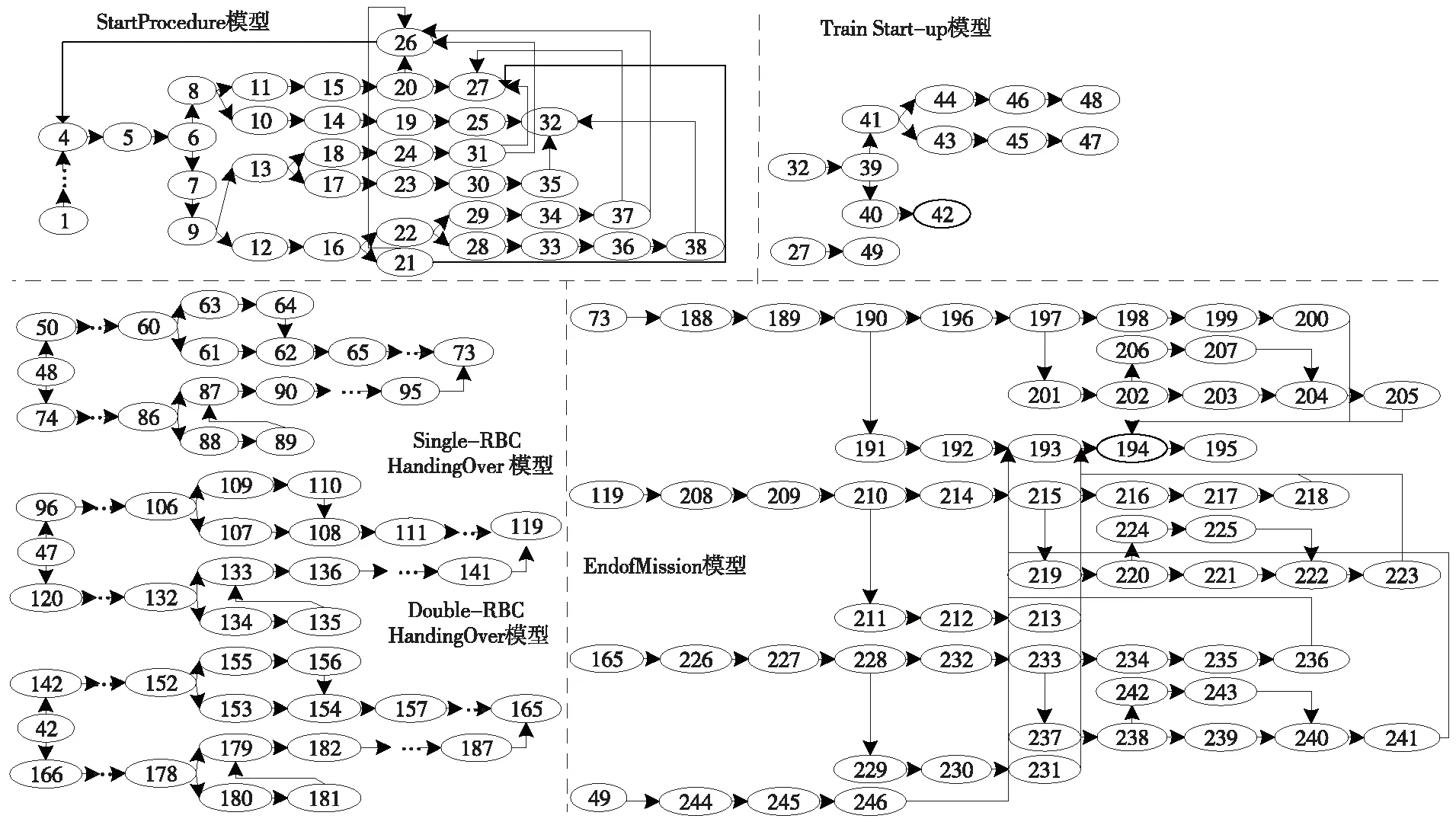
图4 状态空间

表1 底层模型及测试案例对应

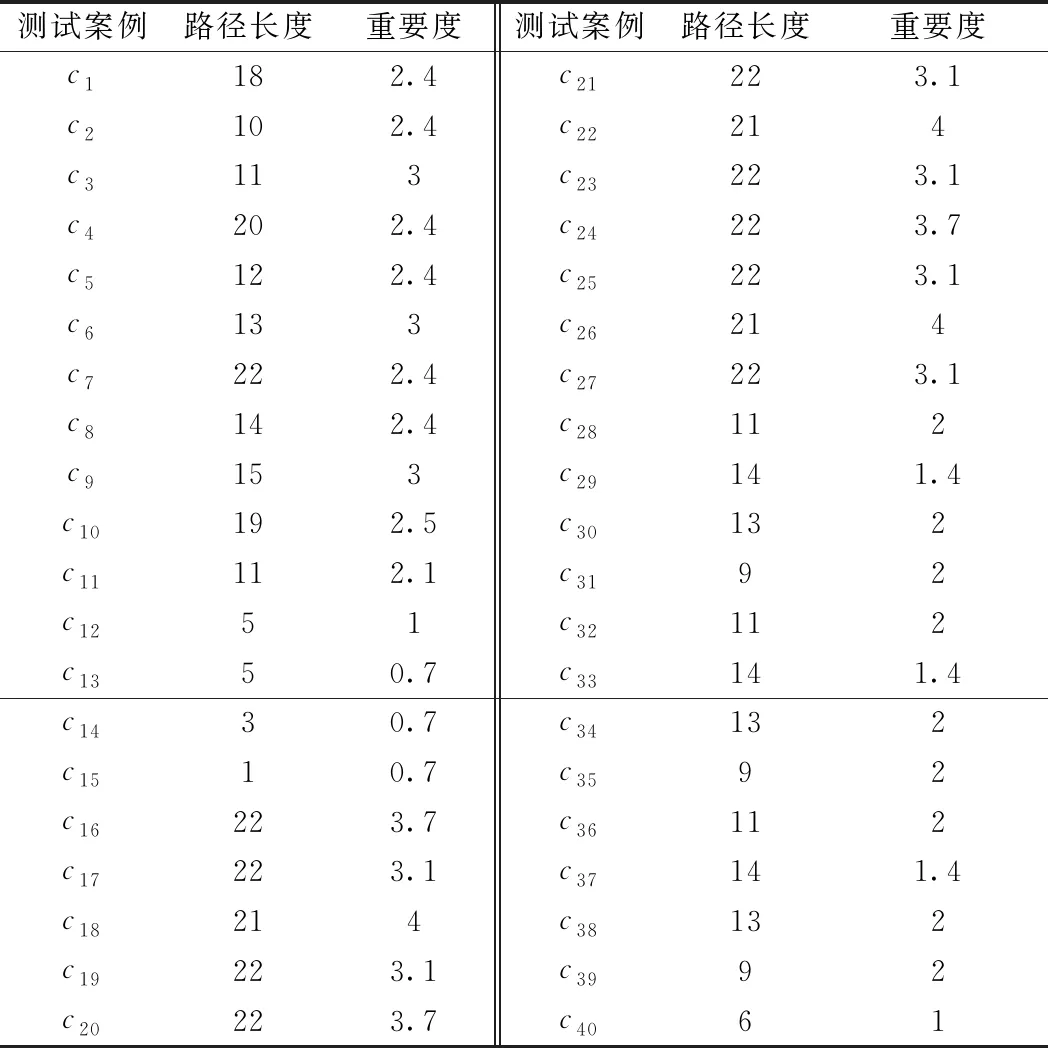
表2 测试案例信息

3.2 算法对比实验

根据DFS算法和场景逻辑关系生成包含152个测试序列的测试序列池，通过本文算法对测试序列池内的测试序列进行选择性地排序，生成最优测试序列集，如表3所示，本文算法和DFS算法的对比结果如表4所示。

表3 测试序列集

表4 不同算法的对比结果

由表3和表4可知：(1)在满足测试案例全覆盖的准则上，基于本文算法生成的测试序列数量远小于DFS算法(即测试序列池的测试序列数量)，测试序列重复度降低86%；(2)本文算法满足测试人员优先执行等极度较高的测试序列，能够及早发现设备问题，及时反馈给相关研发人员，提高并行效率。

4 结语

本文针对多目标测试序列集生成问题，提出一种多目标测试序列集生成方法。该方法根据建模规则构建列控系统模型，并通过测试案例集生成算法生成满足路径全覆盖和节点全覆盖的测试案例集；而后引入3个优化目标，即测试序列重要度、测试序列路径长度和平均测试案例覆盖率，在满足测试案例全覆盖的提前下，提出基于IMMAC的多目标测试序列集优化生成算法，改进了序列遍历策略、信息素更新策略和构造解评价机制等。最后通过实例可知，该方法在满足相应覆盖准则的前提下，具有较高的测试生成效率，为列控系统自动化测试技术的发展提供理论参考。