基于梁-非线性弹簧模型的盾构隧道双层衬砌结构力学特征研究

申兴柱，段军朝，徐朝阳，张 能，王士民

(1.中建三局集团有限公司，武汉 430064； 2.西南交通大学交通隧道工程教育部重点实验室，成都 610031)

引言

随着我国轨道交通建设的日益兴起，采用盾构法施工的城市地铁隧道及铁路隧道数量日益增多。地下工程作为百年工程，使用单层管片衬砌的盾构隧道在施工和运营阶段难免会遇到对隧道结构安全和耐久性产生影响的病害现象。我国第一条水下盾构隧道—打浦路隧道，在使用36年之后衬砌结构出现了混凝土劣化、钢筋锈蚀和渗漏水等影响隧道正常使用的病害问题[1-4]。因此，国内外学者提出在设计阶段考虑或预留二次衬砌施作空间，从而提高隧道结构的使用寿命[5]。

目前，国内外学者主要采用模型试验和数值计算的方法对盾构隧道双层衬砌结构的力学行为进行探究。村上博智和Nasri[6-7]分别开展了盾构隧道双层衬砌整环和多环轴向模型试验，研究了二次衬砌对管片结构的补强效应及承载力的提升效果。张厚美[8-9]按照管片和二次衬砌相互作用形式的不同，建立了3种双层衬砌计算模型，并验证了模型的适用性。王士民[10-11]考虑钢筋对衬砌结构力学行为的影响，基于塑性损伤理论建立了盾构隧道复合结构和叠合结构两种不同类型的双层衬砌计算模型。姚超凡[12]提出了一种用于盾构隧道双层衬砌的计算模型，并采用该模型对不同管片及二次衬砌厚度下的双层衬砌结构的力学行为进行了研究。周济民[13-14]采用相似模型的方法，对盾构隧道双层衬砌结构的横向和纵向力学特征进行了研究，并探究了二次衬砌施作时机和地层差异对双层衬砌结构受力的影响。姚佳兵[15]采用相似模型试验的方法，探究了不同地层、结构类型和二次衬砌厚度等对盾构隧道双层衬砌结构力学特性及破坏模式的影响。阳军生[16]以台山核电站取水隧道为依托，对双层衬砌结构的力学行为进行了监测，根据监测数据提出了相应的荷载取值方法。郭文琦[17]建立纵向分析模型探究了二衬厚度对盾构隧道双层衬砌结构力学行为的影响。

上述研究主要集中在对盾构隧道双层衬砌结构的相互作用计算模型及力学性能两个方面，对不同二次衬砌弹性模量、水压及地层抗力系数条件下的盾构隧道双层衬砌结构横向力学性能尚不明确。鉴于此，以国内某水下盾构隧道为计算实例，基于梁-非线性弹簧模型，建立盾构隧道双层衬砌结构计算模型，探究二次衬砌弹性模量、水压及地层抗力对双层衬砌结构横向力学特性的影响规律，以期为盾构隧道双层衬砌结构的设计和施工提供指导和参考。

1 计算模型的建立

1.1 双层衬砌结构相互作用计算模型

盾构隧道双层衬砌结构的受力特性及承载能力与管片和二次衬砌之间的接合面作用机理密切相关。目前，既有的研究成果将接合面的力学计算模型分为以下3种类型[18-19]。

(1)抗压缩模型：施作二次衬砌前，将管片内周面的手孔、注浆孔等凹槽部位使用充填物做抹平处理，管片衬砌内表面光滑，导致管片与二次衬砌之间只能传递法向压力，不能传递剪力。

(2)局部抗弯模型：二次衬砌混凝土或钢筋植入管片手孔等凹槽部位，此区域可以传递轴力、剪力和弯矩。

(3)抗剪压模型：在施作二次衬砌之前，将管片内周面处的凹槽进行抹平，其余部位进行凿毛粗糙化处理，层间具有较强的黏结力，管片与二次衬砌之间可以传递压力和剪力。

1.2 工程背景

以国内某水下盾构隧道为工程依托，建立盾构隧道双层衬砌结构梁-非线性弹簧抗剪压计算模型，探究水压、地层抗力系数等因素对结构受力及变形的影响。盾构隧道双层衬砌结构如图1所示，管片衬砌选用C50混凝土，弹性模量为34.5 GPa，容重为26 kN/m3，二次衬砌选用C25混凝土，弹性模量为28 GPa。

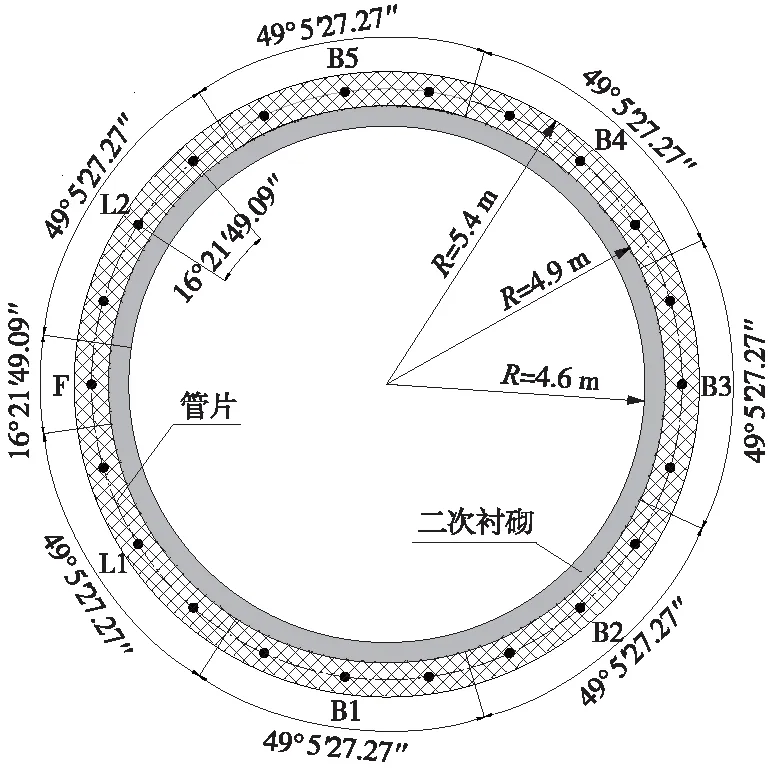
图1 盾构隧道双层衬砌结构示意

1.3 双层衬砌结构横向力学计算模型的建立

梁-非线性弹簧模型采用梁单元模拟衬砌结构的同时，还可以考虑管片接头位置和刚度对结构受力性能的影响。

(1)管片与二次衬砌的模拟

梁-弹簧力学计算模型如图2所示，将管片和二次衬砌采用梁单元进行模拟，梁单元的参数根据管片和二次衬砌截面参数进行取值。

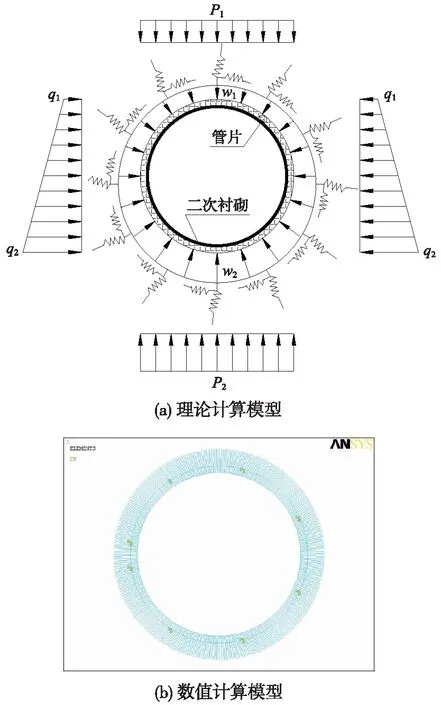
图2 盾构隧道双层衬砌结构计算模型

(2)管片接头的模拟

计算模型中使用弹簧单元等效模拟接头，其中采用抗弯刚度kθ体现管片衬砌环向接头的实际抗弯刚度，接头采用Combine39非线性弹簧单元进行模拟，根据文献[20]得到M-θ关系定义接头单元的参数。同时，采用切向抗剪刚度kt和径向抗剪刚度kr来表征接头的传力特性。

(3)管片与二次衬砌接合面的模拟

根据抗剪压模型的作用机理，管片与二次衬砌之间采用杆单元(仅受压)等效模拟接合面的径向连接，从而保证管片和二次衬砌之间可以传递压力。同时，在接合面间设置切向弹簧单元并采取位移耦合的方法确保层间可以传递剪力。层间压杆的压缩刚度和切向弹簧的刚度取值根据文献[12]进行确定。

(4)荷载施加

盾构隧道衬砌结构在水下地层中受到水土压力的作用，考虑到砂性地层的透水性较强，故采用水土分算的方法计算荷载，土压力加载将其转换为等效节点力。随着隧道埋深变化产生非均匀水压，当拱底和拱顶埋深差越大，非均匀水压的影响越明显。对于大直径盾构隧道，分布在整个盾构隧道管片的水压力呈“灯泡”状[21]。为了实现对作用于管片真实水压的模拟，水压力的施加按照径向荷载的方式，根据水位高度进行计算并施加在结构上，选取埋深30 m，水面距隧道拱顶30 m的断面为标准进行计算分析。本次计算采用均匀水压和非均匀水压分别加载的方式来模拟真实水压作用于盾构隧道管片的实际效果。

2 计算结果分析

2.1 二次衬砌弹性模量对衬砌结构受力的影响

双层衬砌结构中管片和二次衬砌的材料参数选取是极为重要的设计参数，不仅会对整体结构的承载性能产生影响，还会使管片和二次衬砌之间的受力特性发生变化。当地层抗力系数为20 MPa/m，管片衬砌弹性模量保持一定，且二衬厚度为30 cm的情况下，通过改变二次衬砌材料的弹性模量，分析管片结构和二次衬砌受力和变形的变化规律。二次衬砌弹性模量为28.0 GPa的条件下，盾构隧道双层衬砌管片和二次衬砌的弯矩和轴力如图3所示。

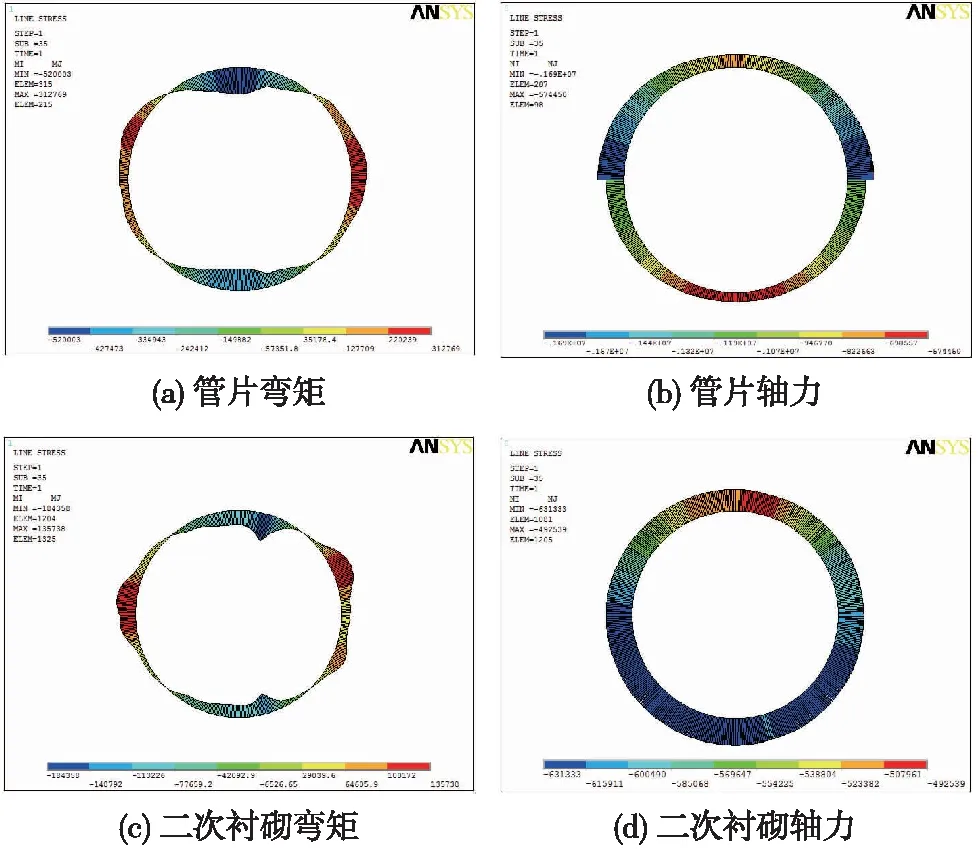
图3 盾构隧道双层衬砌结构内力计算结果

从图3可知，管片和二次衬砌拱顶和拱底±45°区域的结构内侧均处于受拉状态，拱腰内侧呈受压状态，两者轴力均处于受压状态，与结构的实际内力分配规律相吻合。在管片环向接头部位，由于接头的存在导致管片在该区域局部刚度较低，外荷载作用下产生较大的变形，此部位管片与二次衬砌贴合紧密，相互作用效应更为显著，管片和二衬结构在部位的弯矩均出现了突变，其中管片结构在此处的弯矩小于附近区域，二次衬砌结构在接头处承担了较大的弯矩。从量值来看，管片衬砌所承担的内力量值均大于二衬结构的内力值，表明管片仍是主要的承载结构。不同二次衬砌弹性模量下衬砌结构的内力变化曲线如图4所示，内力最大值统计见表1。

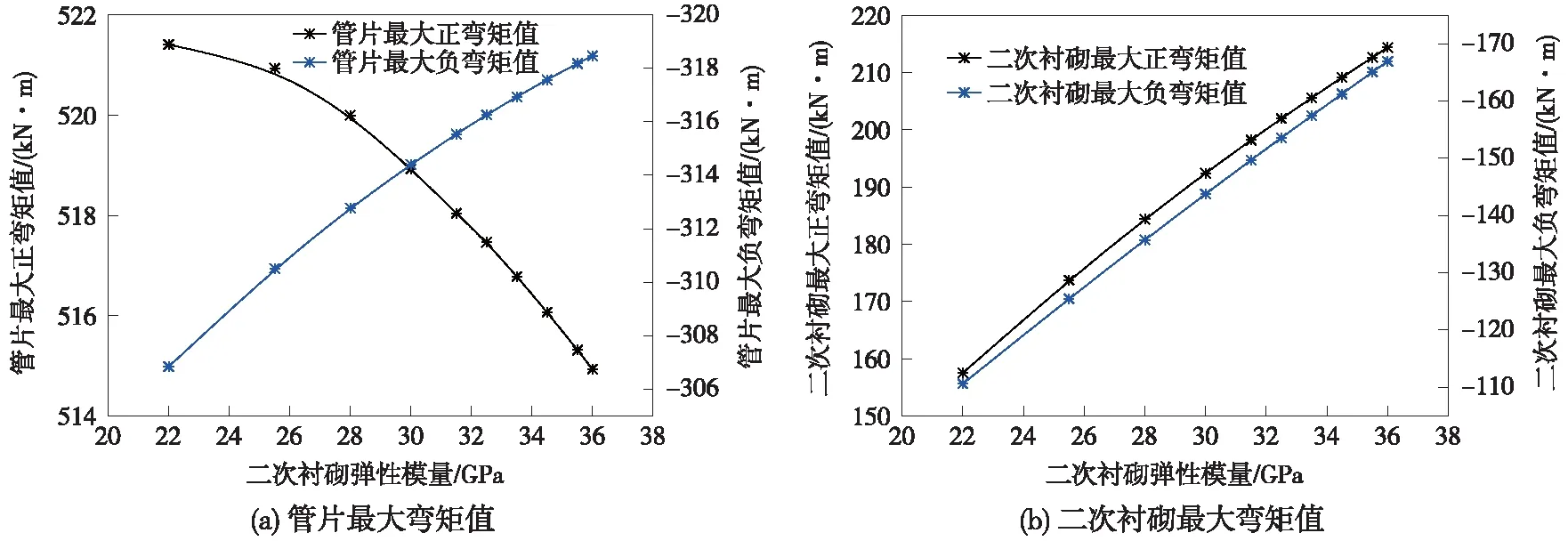
图4 双层衬砌结构最大弯矩值随二衬弹性模量变化曲线

从图4可以看出，随着二次衬砌弹性模量的增大，二次衬砌的弯矩值均呈增大的趋势，而管片结构的最大正弯矩呈增大趋势，最大负弯矩呈减小的趋势。当二次衬砌弹性模量由22.0 GPa增大至36.0 GPa的过程中，二次衬砌的最大正、负弯矩值分别增大了56.89 kN·m和56.33 kN·m，呈线性增加的变化趋势。从弯矩的变化幅度来看，二次衬砌弯矩增幅较管片弯矩量值的变化幅度更为明显。同时，随着二次衬砌弹性模量的增加，管片最大正、负弯矩所对应的轴力值呈降低的趋势，而二次衬砌最大正、负弯矩所对应的轴力量值呈增大的变化规律，增大二次衬砌的弹性模量在一定程度上可以改善二次衬砌的受力状态。

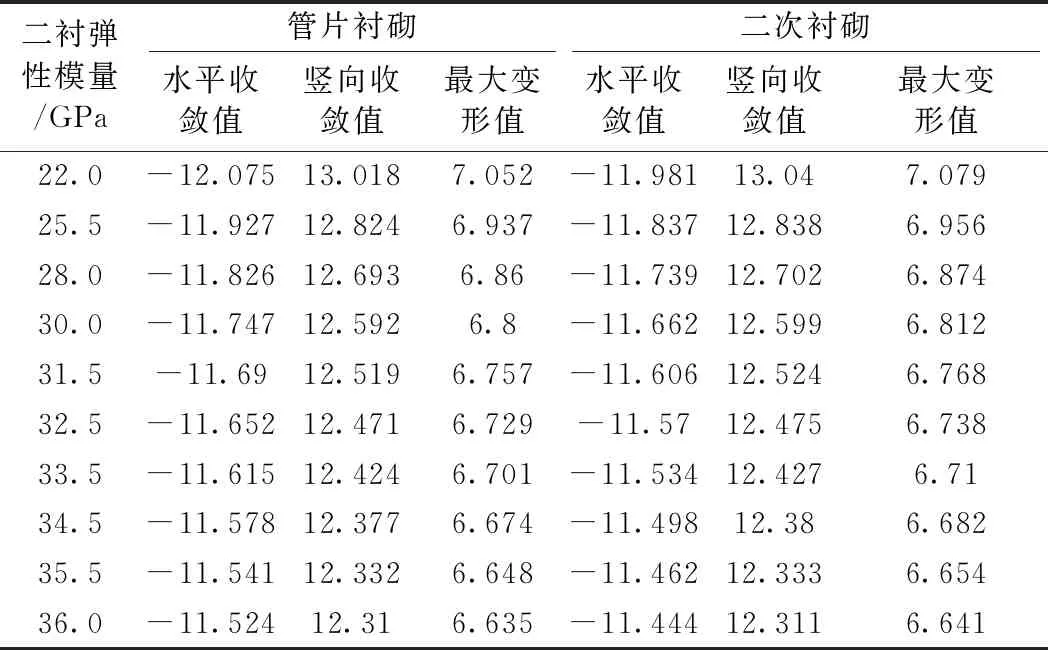
表1 不同二次衬砌弹性模量下双层衬砌变形结果 mm

从表1可知，随着二次衬砌弹性模量的增加，结构整体的刚度增大，在外荷载一定的条件下，衬砌结构的变形均呈减小的趋势。二次衬砌弹性模量由22.0 GPa增加至36.0 GPa时，管片结构的最大变形值同比减小了5.9%，二次衬砌的最大变形值减小了6.19%。从量值上可以看出，在此条件下，管片和二次衬砌的最大变形值均出现在拱顶处。由于此区域的层间相互作用不显著，引起管片和二衬产生了非协调变形，导致管片结构的最大变形量普遍小于二次衬砌的变形值。

2.2 不同水压条件下的双层衬砌结构力学特征

水下盾构隧道在穿越渗透系数较大的砂性地层时，同时还将面临较大的水压，衬砌结构的受力性能在一定程度上会受水位变化的影响。为此，选取30 m上覆土压力，地层抗力系数为20 MPa/m、侧压力系数为0.3的工况，通过改变水压力的大小，获得盾构隧道双层衬砌结构在不同水压条件下的受力及变形特性。水压为10 m和60 m条件下的双层衬砌结构轴力分别如图5、图6所示。

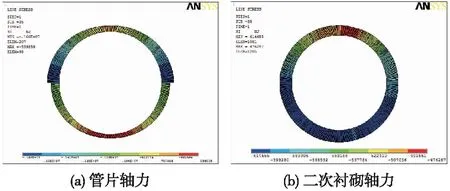
图5 双层衬砌结构轴力云图(水压为10 m)

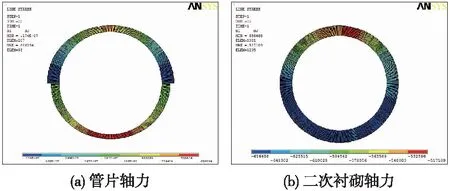
图6 双层衬砌结构轴力云图(水压为60 m)

从图5、图6可以看出，管片和二次衬砌结构轴力均呈受压的状态，水压的增加，有效地提升了管片结构的轴力水平，在一定程度上可以改善结构的受力状态，从而使得管片承受荷载的能力增强。图7为不同水压条件下双层衬砌结构内力与变形的变化曲线。

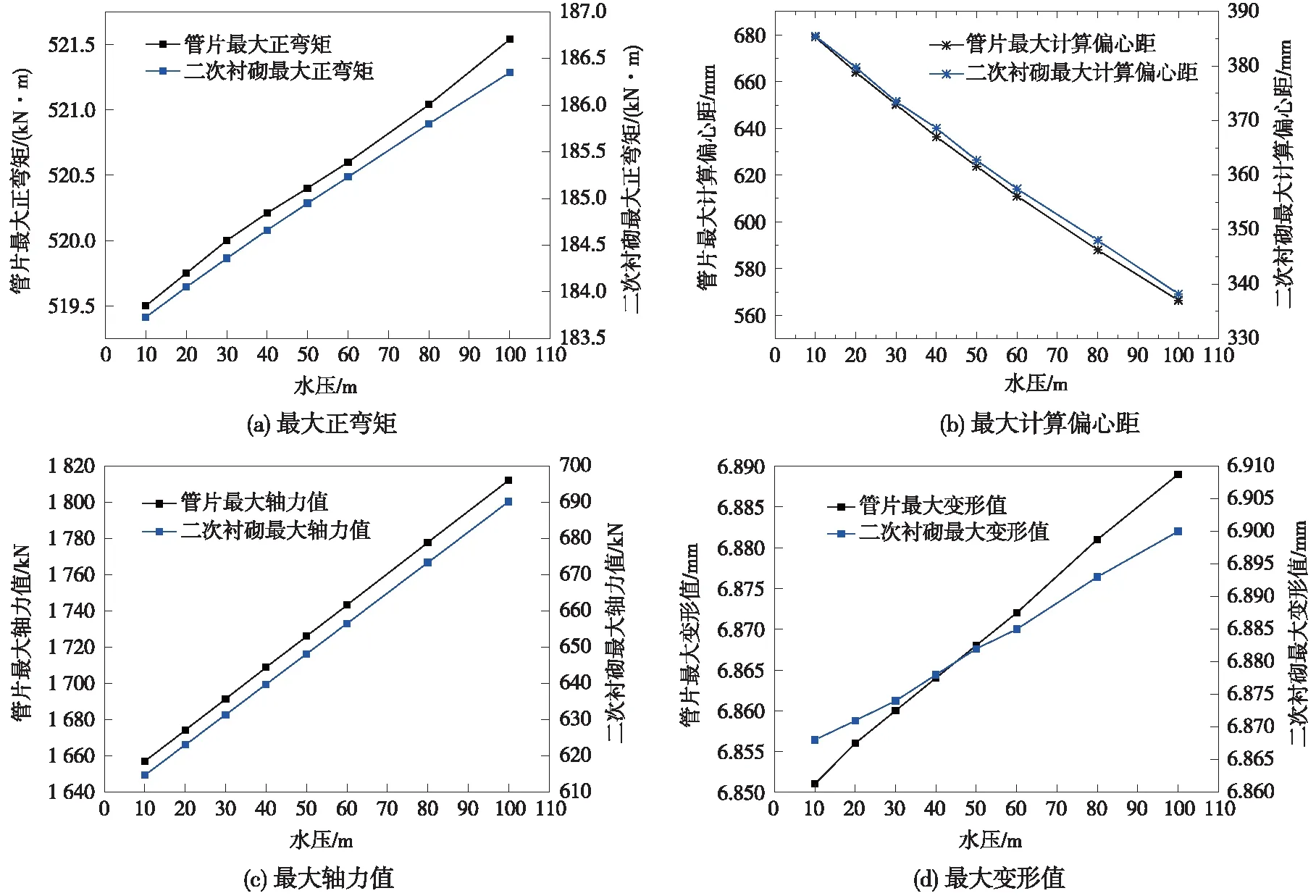
图7 不同水压条件下双层衬砌结构内力与变形的变化曲线

由图7可知，随着外部水压力的增大，管片结构的弯矩和轴力呈逐步增大的趋势，但弯矩的增长幅度较小，水压力的增加进一步提高了衬砌结构的轴力水平，从而导致管片与二次衬砌结构的最大计算偏心距呈线性减小的趋势。水压从10 m增大至60 m的过程中，管片结构的轴力峰值增大5.21%，二次衬砌的轴力峰值增大了6.81%；管片的最大计算偏心距由679.11 mm减小至610.98 mm，减小的幅度为10.03%，二次衬砌结构的最大计算偏心距由385.53 mm降低至357.48 mm，同比减小7.27%，外水压力的增大在一定程度上对改善管片结构的受力状态更为有利。同时随着水压的增加，隧道衬砌结构的最大变形值亦呈增大的趋势，但是增幅并不显著。

2.3 不同地层抗力系数下双层衬砌结构力学特征

隧道结构是由围岩和衬砌结构共同构成并存在相互作用的支护体系。隧道所处地层不仅会直接影响衬砌结构的受力特性，同时还会对隧道结构的承载能力产生显著影响。鉴于此，根据盾构隧道岩土勘察报告，选取地层侧压力系数为0.3情况下，不同地层抗力系数对衬砌结构受力和变形的影响规律。图8为地层抗力系数为2.5～60 MPa/m情况下的双层衬砌结构内力分布变化曲线。当隧道结构位于软弱地层时，隧道周围地层不能给衬砌结构提供较好的约束作用，荷载作用下衬砌结构的变形无法得到有效控制，从而导致衬砌的变形和内力对隧道结构的承载均处于不利状态。

从图8可以看出，地层抗力系数会对双层衬砌结构的受力产生显著的影响。随着地层抗力系数的增大，管片和二次衬砌的最大正、负弯矩值均呈减小的变化趋势，在地层抗力系数小于30 MPa/m时，弯矩的变化幅度较为显著，当地层抗力系数大于30 MPa/m后，结构的弯矩变化幅度趋于平稳。在地层抗力系数由2.5 MPa/m增大至60 MPa/m的过程中，管片最大正弯矩值减小70.59%，最大负弯矩值减小82.43%；二次衬砌的最大正弯矩值减小85.64%，最大负弯矩减小84.04%，二次衬砌弯矩的减小幅度更为显著。从结构轴力峰值的变化情况来看，随着地层抗力系数的增加，管片结构的轴力峰值呈增加的趋势，而二次衬砌的轴力峰值呈先增加后减小的变化规律，但是结构整体的轴力水平呈增大的趋势，从而大幅改善了结构的受力状态。从最大计算偏心距的结果可知，随着地层条件的进一步改善，降低了管片和二次衬砌结构的偏心距量值，从而更加有利于结构的受力和承载性能。图9为双层衬砌结构变形情况随地层抗力系数变化曲线。

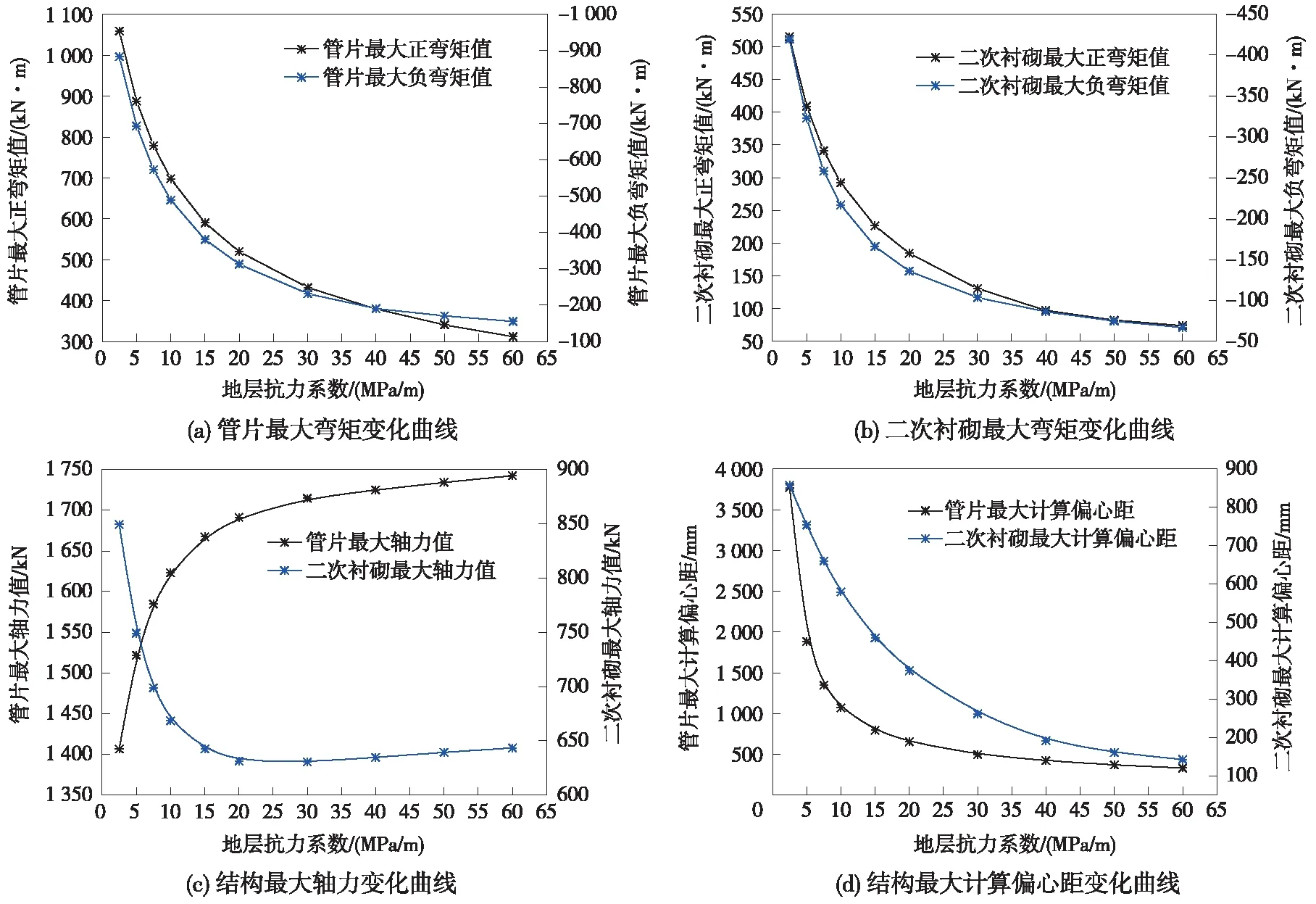
图8 双层衬砌结构内力分布随地层抗力系数变化曲线

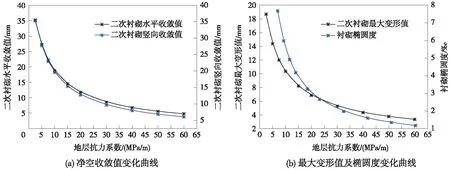
图9 双层衬砌结构变形情况随地层抗力系数变化曲线

从图9可知，隧道净空收敛值和最大变形值随地层抗力系数的增大总体呈非线性的减小趋势，当地层抗力系数达到30 MPa/m时，结构的变形随地层抗力系数的增加逐步趋于稳定。当地层抗力系数为2.5 MPa/m时，由于封顶块位于此部位，导致结构局部刚度较低，衬砌结构的最大变形值出现在左拱腰处；随着地层抗力系数的增大，衬砌结构的最大变形值转移至拱顶和拱底处。地层抗力系数由2.5 MPa/m增大至20 MPa/m时，管片结构的最大变形量降低63.28%，二次衬砌的最大变形量同比减小62.76%。由此可以看出，隧道周围地层的抗力系数对衬砌结构的变形会产生显著的影响，当地层抗力系数越大时，对衬砌结构变形的约束作用越为显著，可进一步提高衬砌结构的承载能力。

3 结语

本文基于梁-弹簧理论，考虑管片环向接头的非线性特征，建立了盾构隧道双层衬砌结构抗剪压计算模型，探究了二次衬砌弹性模量、水压及地层抗力系数对盾构隧道双层衬砌结构横向受力和变形的影响规律，通过上述研究主要得出以下结论。

(1)随着二次衬砌弹性模量的增大，管片最大正弯矩呈减小的变化趋势，最大负弯矩呈增大的趋势，二次衬砌的最大正负弯矩值均呈增大的变化规律。同时，衬砌结构的整体轴力水平随着二次衬砌弹性模量的增大而逐步提升。

(2)水压的存在对圆形衬砌结构产生环箍作用，在一定范围内其量值的增加进一步提高了衬砌结构的轴力水平，导致管片和二次衬砌结构的最大计算偏心距呈减小的趋势。当水压由10 m增加至60 m，管片和二次衬砌结构的最大计算偏心距分别减小10.03%和7.27%，从而在一定程度上可以改善衬砌结构的受力状态。

(3)当地层抗力系数小于30 MPa/m时，管片和二次衬砌结构的弯矩受地层抗力系数的影响较为明显；在地层抗力系数由2.5 MPa/m增大至60 MPa/m的过程中，管片结构的最大正、负弯矩值分别降低70.59%和85.64%，二次衬砌的最大正、负弯矩值同比减小85%，衬砌结构的轴力水平整体上得到了提升，结构的计 算偏心距也呈减小的趋势；管片和二次衬砌的最大

变形量分别减小63.28%和62.76%，软弱地层对双层衬砌结构的稳定性会产生显著影响。