双线盾构隧道下穿机场跑道沉降特征分析

张恒新，张孟喜，王晓鸿，李 磊

(1.上海大学土木工程系，上海 200444； 2.上海机场(集团)有限公司，上海 200335； 3.上海隧道工程股份有限公司，上海 200032)

随着我国经济实力的快速提升，民用机场的建设呈现出蓬勃发展的势头，但由于受当时特定条件的限制，先前的机场规划建设大都没有考虑预留供地铁或者公路下穿的隧道。随着交通的日益拥堵，为改善机场周边的交通状况，越来越多下穿机场飞行区的隧道工程需要建设。盾构法因具有施工速度快、对地面扰动小、不影响地面交通等优点被广泛应用到隧道建设中[1]。但即使盾构施工，也不可避免地会对穿越区土体造成扰动，进而导致跑道等机场设施发生沉降。由于机场跑道对沉降的要求极其严苛，沉降控制不力轻则造成跑道开裂、机场停运，重则可能会酿造机毁人亡重大事故。因此，研究盾构下穿施工引起的跑道沉降规律具有十分重要的意义。

目前，国内外对于盾构法施工下穿既有建筑物、构筑物等引起的上方沉降方面做了大量的研究，对于下穿机场跑道引起道面沉降规律的研究还很少。在理论公式方面，计算盾构施工引起地表沉降方法主要有Peck公式[2]和Sagaseta公式[3]。后续学者研究得到盾构施工引起的三维地表沉降计算公式[4-7]。在数值模拟方面，现有研究多集中于盾构隧道覆土深度、土仓压力、注浆压力等施工参数对于跑道沉降的影响[8-13]。此外，还有部分学者结合现场试验及现场监测做了相关下穿机场跑道研究[14-19]。

综上所述，目前研究主要集中在优化盾构施工参数，来减小对跑道面沉降的影响，很少涉及双线盾构施工对跑道沉降规律的影响分析。本文暂不考虑飞机荷载作用，通过数值模拟深入探究双线盾构下穿对机场道面沉降的影响规律，并与既有研究成果和现场监测数据进行对比分析，试图找出跑道沉降的最大位置，以期能够为今后类似盾构下穿机场跑道工程提供指导。

1 工程背景

1.1 工程概况

上海地铁10号线空港一路站—虹桥东站区间下穿虹桥机场飞行区工程，主要下穿机场草坪、滑行道和跑道(图1)。该下穿工程采用土压平衡盾构施工，盾构机外径Φ=6.34 m，隧道衬砌外径R=6.2 m，采用0.35 m厚、1.2 m环宽的预制钢筋混凝土管片。双线隧道间距12 m，隧道最大埋深约24 m。

图1 盾构隧道穿越机场平面示意

1.2 工程地质条件

根据岩土工程勘察报告，下穿场区的75 m深度范围的地基土由第四纪全新统至上更新统沉积的地层组成，主要有：①褐黄-灰黄色黏土、②灰色淤泥质黏土、③灰色粉砂与灰色粉质黏土、④灰色粉质黏土等，具体地层物理力学参数见表1。

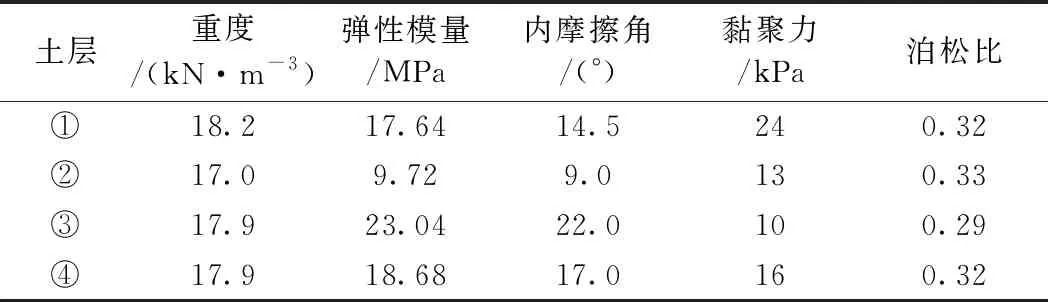
表1 土层物理力学参数

1.3 工程难点

(1)跑道沉降变形要求高:下穿过程引起的跑道最大沉降不能超过10 mm，最大倾斜不能超过0.1%，给施工带来极大的挑战。

(2)穿越影响范围大：盾构穿越机场跑道中段，隧道处在现有飞行区的影响范围约540 m，要严格控制影响范围内的道面沉降。

(3)现场监测受限：监测设备不能进入滑行道及跑道禁区，施工监测需要满足飞机正常起降，同时又要保证监测准确性，实施难度极大。

2 穿越施工模拟

选用ABAQUS有限元分析软件建立数值模型，模拟盾构施工过程对跑道及地层沉降的影响。模型的几何尺寸为80 m(x)×120 m(y)×45 m(z)，隧道长120 m，内径5.5 m，外径6.2 m，隧道间距12 m。飞机跑道宽度为45 m，厚度为1 m。双线隧道下穿机场跑道的数值模型见图2，模型顶面无约束，其他面施加法向约束。

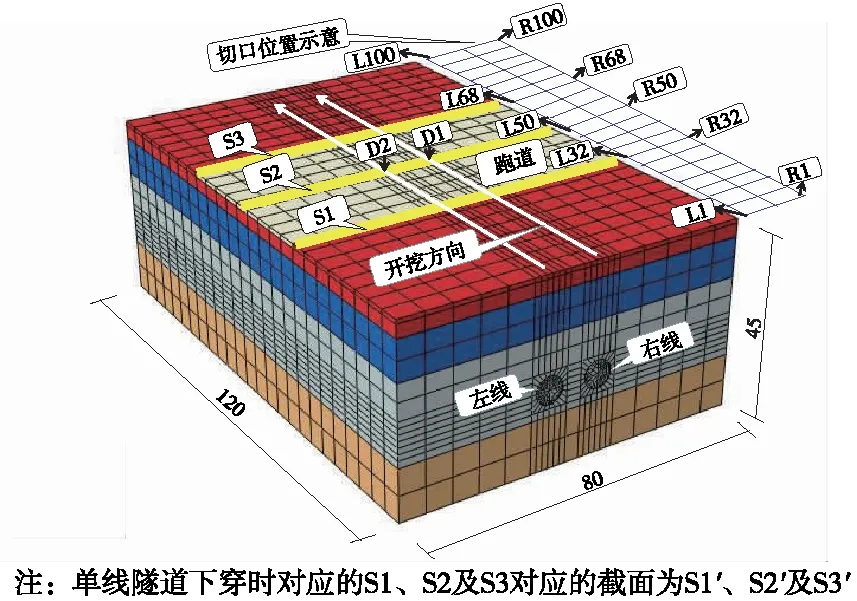
图2 数值模型(单位：m)

模型单元采用实体C3D8单元，土体采用Mohr-Coulomb本构模型，土体与衬砌管片接触面采用绑定约束。盾构机、隧道管片和注浆采用线弹性材料模拟。机场跑道由块石层、混凝土层及沥青层等组成，如图3所示。为了计算的方便，将跑道简化为弹性模量为10 000 MPa的线弹性材料。表2所示为除土体外其他模型材料参数。本文暂不考虑土中水的渗流作用和土的固结作用，模拟双线隧道盾构下穿机场跑道情形。

图3 跑道结构

表2 模型材料参数

隧道开挖模拟采用单元生死法，如图4所示。为计算方便，可以在不影响计算精度条件下，设置每2个管片的宽度(2.4 m)为一个开挖步，模型共有14 375个单元，17 212个节点。

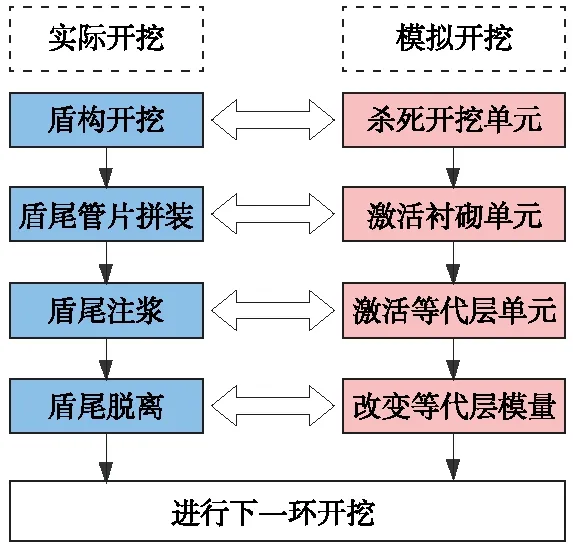
图4 隧道开挖模拟过程

3 结果分析

3.1 跑道纵向沉降槽分析

文献[9]研究了单线隧道下穿引起的跑道沉降特征，在此基础上，重点研究双线隧道下穿对跑道的沉降影响。单线隧道下穿完成后，沿跑道纵向S1′、S2′及S3′断面(对应于双线数值模型S1、S2、S3截面)处地表沉降曲线呈现出典型的“V”形沉降槽，与Peck曲线相一致，最大沉降点位置位于隧道的正上方，如图5所示。由图5可以看出，在双线隧道下穿完成后，最大沉降位置偏移到了右线隧道左边缘对应的地表处。这是因为右线隧道先开挖，左线隧道后开挖，右线隧道上方的土体发生两次扰动，因此右线隧道上方区域跑道沉降较大。

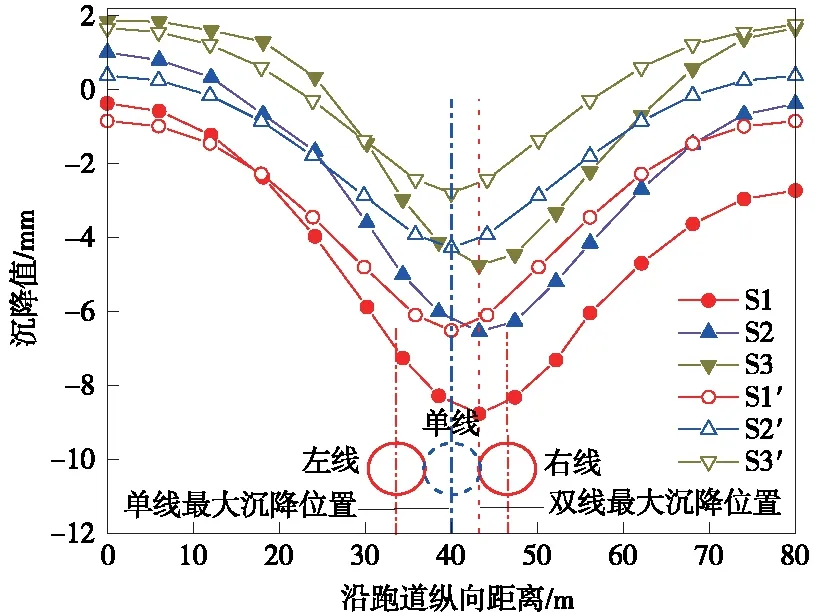
图5 跑道不同截面处地表沉降曲线

双线隧道下穿完成后，分别取跑道左边缘(S1)、跑道中心线(S2)及跑道右边缘(S3)处截面为监测面观测跑道面沉降，并且对比单线隧道下穿条件下的跑道S1′、S2′及S3′截面的跑道沉降值。可以看出，不同截面处双线隧道盾构下穿引起的跑道最大沉降始终要大于单线下穿时的跑道最大沉降。

不同监测截面处的单、双线隧道下穿引起的最大沉降值对比如表3所示，由表3可知，不同截面处最大沉降差值都约为2 mm。单线下穿引起的跑道最大地表沉降约为6.6 mm，双线隧道下穿引起的跑道最大沉降达到了8.9 mm，都未超过10 mm的限值。但是双线下穿时跑道最大沉降已经接近于限值的要求，此时应考虑调整盾构施工参数或者对土体进行加固处理，以减小对跑道沉降的影响。

表3 单、双线下穿不同监测面最大沉降对比 mm

双线隧道下穿过程中，盾构开挖到不同切口位置处时，跑道面中心线的沉降变化曲线如图6所示。由图6可知，右线隧道先行开挖到R32环(接近跑道下方)时，跑道中心线整体沉降呈微隆起。到R50环(跑道中心线下方)时，跑道沉降呈现出V形沉降槽。开挖到R68环(开始远离跑道)时，沉降继续增大，最大为5.8 mm左右。随着后续左线隧道开挖的进行，跑道中心线的最大沉降仅少量增加，L68环时最大沉降值为7.4 mm。

图6 不同切口位置处跑道中心线沉降曲线

双线隧道下穿完成后，跑道中心线处的地表沉降如图7所示，可以看出，模拟值与实测值基本吻合，且模拟值基本大于现场实测值，最大差值不超过2 mm。由图7可以看出，现场监测与数值模拟沉降曲线都呈现出Peck曲线的形状，为不完全对称的“V”形沉降槽，而非“W”形沉降槽。参考文献[20-21]关于双线隧道下穿引起沉降槽形状研究成果，双线盾构隧道下穿引起的地表沉降槽的形状与隧道间距(L)、隧道埋深(H)及隧道半径(R)都有关系，当L/(H+R)≤0.5时，沉降槽呈现“V”形。随着L增大，土体最大沉降逐渐减小，沉降槽宽度增大，沉降曲线形状由“V”形转变成“W”形。本文双线盾构下穿时的L/(H+R)=0.44，符合“V”形沉降槽的特征。

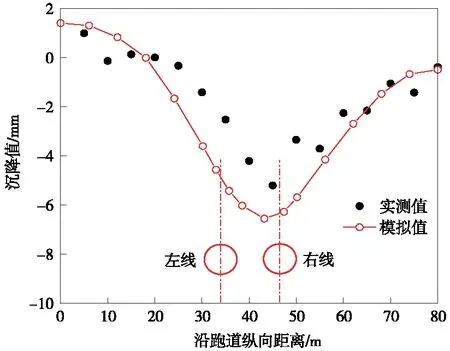
图7 跑道中心线沉降曲线对比

3.2 开挖方向沉降分析

沿隧道开挖方向，对比双线隧道下穿条件下有跑道结构和无跑道结构(跑道区域材料赋值成土体材料)时右线隧道左边缘处对应地表最大沉降，具体如图8所示。可以看出，草坪段(0～38 m最大沉降分别为10.2 mm和15.2 mm。在跑道段(38～83 m)最大地表沉降呈现线性减小，跑道左边缘处最大沉降分别为8.9 mm和11.8 mm，跑道右边缘处的最大沉降分别减小到了4.8 mm和7.8 mm。跑道结构的存在能够明显减小地表沉降，这是由于跑道结构相较于土体，其本身刚度巨大，不仅跑道自身沉降较小，而且跑道的存在还能够极大的限制周围土体的变形，对于减小土体沉降起到有益作用。

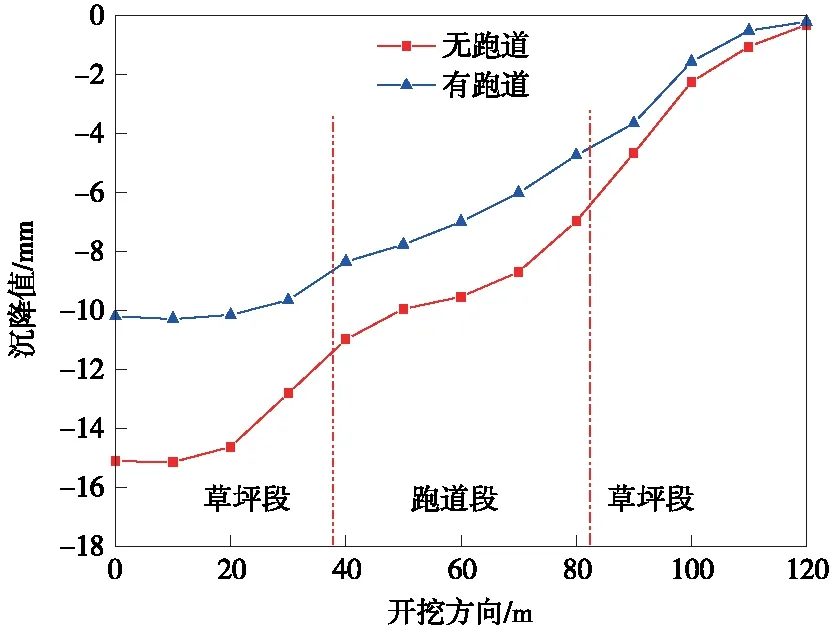
图8 开挖方向沉降曲线对比

图9 开挖到跑道中心线下方跑道沉降曲线对比

双线隧道先进行右线下穿，后进行左线隧道下穿。右线隧道开挖到跑道中心线下方时，隧道中心线上方跑道沉降如图9(a)所示，左线隧道开挖到跑道中心线下方时，跑道沉降如图9(b)所示。由图9分别可知，数值模拟结果与现场实测结果沉降曲线趋势基本一致，数值模拟结果最大沉降与现场实测基本吻合，同时跑道最大倾斜率约为0.01%，远小于0.1%的限值，符合现场施工的要求。通过结果对比，证明了数值模拟结果的有效性，可为施工过程沉降预测提供一定指导。

3.3 特征点沉降分析

特征监测点D1沉降随右线开挖过程变化曲线见图10(a)，特征监测点D2沉降随左线开挖过程变化见图10(b)，由图10可知，数值模拟结果与现场实测数据都具有很好一致性，沉降变化都呈现出“先微隆起，再沉降逐步增大到稳定值”的趋势，且数值模拟结果基本大于现场实测值，最大沉降差为1 mm左右。

图10 特征点沉降随开挖步变化对比

选取跑道不同截面S1、S2及S3上的最大沉降位置(右线隧道左边缘对应地表处)3个点为特征点，监测双线隧道盾构下穿施工过程中，特征点随开挖步的沉降变化，沉降曲线具体如图11所示。由图11可知，双线隧道下穿施工引起的3个特征点的沉降曲线都表现为：先隆起，后沉降，再沉降量少量减小，最后沉降又增大到稳定值。

双线隧道下穿使特征监测点受到两次扰动，进而导致特征点发生两次沉降过程。由图11可以看出，双线盾构隧道下穿引起的特征点沉降主要发生在右线隧道施工过程中。表4所示右线下穿导致的特征点最大沉降量约占总沉降量的85%。这是因为右线隧道先下穿，导致最大沉降点靠近右线隧道，左线隧道施工后下穿，对特征点沉降扰动要远小于初次扰动的影响。所以，在双线盾构隧道施工过程中更应该控制好初次扰动对跑道沉降的影响，以保证机场安全运营。

图11 特征点沉降变化

表4 不同特征点沉降

4 结论

以上海地铁隧道下穿虹桥机场跑道为背景，主要分析了双线盾构隧道下穿引起的跑道沉降规律，并结合现场监测数据与既有研究成果，主要得出了以下结论。

(1)通过对比不同监测面的单双线隧道下穿引起的跑道面最大沉降，双线隧道下穿引起的跑道左边缘截面S1处地表最大沉降为8.9 mm，已接近10 mm限值，此时应采取调整施工参数或对土体加固等措施来减小跑道沉降。

(2)双线隧道下穿完成后，地表最大沉降发生在右线隧道左边缘上方地表处，模拟结果与现场实测数据沉降趋势一致，地表沉降槽均呈现“V”形而不是“W”形。本文中双线隧道下穿时的L/(H+R)=0.44，符合“V”形沉降槽的特征。

(3)双线盾构隧道下穿条件下，跑道的存在极大地限制了周围土体的变形，对于控制土体沉降起到有益作用。双线隧道上方地表沉降的模拟结果与现场实测数据最大差值不超过2 mm，跑道的最大倾斜率为0.01%，远小于0.1%的限值要求。

(4)特征点沉降曲线呈现“先隆起，后沉降，再沉降量少量减小，最终沉降增大到稳定值”趋势。并且特征点总沉降量中，右线隧道施工导致的最大沉降点的沉降占到总沉降量的85%左右。因此，双线隧道盾构施工过程中更应该控制好初次扰动，以减小对机场跑道沉降的影响。