考虑多土层的波-流荷载下跨海桥梁桩基动力响应分析

潘 良，祝 兵，张家玮，康啊真

(西南交通大学土木工程学院，成都 610031)

桩基础具有承载力高、基础沉降小等优点，且桩的布置方式灵活多变，设计时可通过调整桩的数目及布置来满足桥梁结构的使用性能要求，因而在桥梁工程中广泛应用[1]。其中跨海大桥所处的海洋环境十分恶劣，设计使用年限内承受着风、浪、流、潮汐、地震等多种环境荷载作用，波流力作为工程设计的控制荷载[2-3]，尤其对于承受上部结构的桩基而言更是主导荷载，它严重影响整个工程的造价、安全性以及工程的使用寿命。一旦桩基结构遭到破坏，整个海洋工程结构将会蒙受不可估量的损失。因而研究波流力对桩柱结构的作用是很有必要的。

对于小直径桩柱所受的波浪力，工程实际计算中仍采用Morison公式。桩基结构在波流荷载下的动力响应分析中，赵晖[4]采用Winkler弹性地基梁模型模拟桩-土动力的相互作用，由解析法给出了埋置圆桩在波-浪-流场下的动力响应。沈锦宁[5]将桩离散成多质点系，用水平土弹簧计算土抗力，研究了波浪作用下单桩基础的动力响应。胡丹妮[6]利用Ansys软件建立桩-土三维有限元模型并引入p-y曲线修正，计算波浪荷载对桩基的动力响应。周静姝[7]用Ansys软件建立桩-土三维有限元模型，计算实际工程中波浪荷载对多土层桩基的响应。付鹏[8]采用三维数值分析方法，建立了考虑流固耦合的三维桩-土模型，来模拟波浪对桩及海床的直接作用。大多数研究并未考虑到波浪与流的相互作用及KC数对水动力系数的影响，以及多土层土体下的桩土相互作用。

本文基于Morison方法得到不同参数的波-流荷载，根据实际工程利用Abaqus有限元软件建立桩-土相互作用模型，来研究波-流荷载作用下，桩基础分别在实际多土层土体与单土层土体情况下的动力响应，以及不同波流荷载工况下单桩与群桩响应随荷载参数的变化，为实际工程计算提供参考。

1 工程概况

本研究依托在建甬舟铁路金塘特大桥的基础土层和水文条件[9]。金塘特大桥全长8 722.65 m，跨海段长5 188.265 m，其中金塘水道上为公铁合建双塔悬索桥(112+224+1 050+238+42) m。桥址处为台风影响区，强风天气天数多。年平均波浪高1.14 m，最大波高6.1 m。

索塔墩位处水深49 m，金塘航道桥立面与索塔墩位处群桩桩基布置见图1。其中，群桩由34根单桩与承台构成，桩柱沿纵桥向分为4排，中间两排各9根，前后两排各8根，排间距9 m，每排中，桩心距为9 m，单根桩长129 m，桩径4.5 m，桩基混凝土采用C50。

2 模型建立

现针对施工阶段单桩与索塔墩下群桩建立实际情况下的多土层模型，以及单土层模型a(土体全为土层1粉土性质)、单土层模型b(土体全为土层2粉砂性质)、固接模型(不考虑桩土相互作用，在泥面高度处固接桩体)作对比分析。三类单桩模型土层示意见图2。

图2 三类单桩模型土层示意

2.1 材料与接触设置

桩基弹性模量为3.4×104MPa，密度为2.5 t/m3。土体采用摩尔-库伦模型。在Abaqus中采用分区功能划分土层并赋予其对应的性质，由上到下按土层序号设置材料参数、接触摩擦属性与预应力侧压力系数。桩侧与各土层土体接触均设置为面-面接触，以桩基为主面，土体为从面，法向接触类型为硬接触，切向摩擦为罚摩擦[10]。各土层土体相关物理力学参数如表1所示。

2.2 网格划分

单桩模型土体尺寸为150 m×150 m×260.43 m；群桩模型土体尺寸为760 m×760 m×260.43 m。单桩桩长129 m，直径4.5 m，埋深86 m，入水深度43 m。桩基与土体均采用C4 D8单元，并在桩土接触区域细化土体网格，保证接触处土体网格尺寸小于桩身网格。单桩桩顶自由，群桩各组成桩的尺寸同单桩模型，顶部有承台固接约束。建立单桩、群桩模型如图3所示，总体网格数单桩模型约13万个。研究中采用的简化群桩模型与未简化的群桩模型进行了计算对比，误差在1%以内。为了提高计算效率，采用简化后的群桩模型计算，简化后的群桩模型总体网格数约18万个。

表1 土层物理力学参数

2.3 波-流荷载计算

计算波-流荷载的方法有多种[11-12]，本文不考虑波浪力的非线性[13]，采用有流参与的Morison公式计算圆截面桩受到的波流荷载，并参考JTS145—2015《港口与航道水文规范》，根据KC数选取不同工况下对应波流荷载的水动力系数Cd，Cm。其中KC数根据式(1)计算，Umax为表面水质点最大水平速度，T为周期，D为圆柱桩直径。土体上施加对应49 m水深的静水压力，并在地应力平衡分析步采用导入应力场的方法。

(1)

图4 波-流荷载沿桩分布

利用Matlab计算考虑波流相互作用的桩基波流力。对于群桩，又考虑了不同组成桩间的波流荷载相位差。图4为计算得到的单桩某一波流荷载沿桩分布情况。图5为群桩各组成桩的编号与波流荷载入射平面示意。本文计算采用隐式瞬态分析步，忽略前段的瞬态响应，取最终的稳态响应为结果。

单桩与群桩所有波流荷载工况参数范围根据甬州铁路金塘大桥桥址处水文资料拟定。

图5 群桩布置形式与波流荷载入射示意

3 不同土层模型的影响

3.1 不同模型的动力响应

为了解四类模型的单桩在相同波流荷载下的响应差异，设定波流荷载周期为5 s，波高1.8 m，流速1.0 m/s，计算四类模型的稳态响应。如图6(a)为四类模型稳态时桩顶参考点沿波流向位移Y的时程变化，由图可见多土层模型与单土层模型a稳态时桩顶位移几乎重叠，且位移峰值与幅值均大于单土层b模型，明显大于泥面处固接模型；前三类模型桩身最大主应力出现在桩基迎波流向的泥面稍下处，固接模型最大主应力在泥面固接处，以各类模型桩身最大主应力为参考应力S，如图6(b)为四类模型稳态时最大主应力的时程曲线，前三类模型最大主应力时程曲线几乎重叠，其峰值均大于固接模型。

图7为四类模型稳态时，以泥面处为零点，沿桩身的弯矩内力包络图，泥面固接模型的最大弯矩远大于前三类模型，多土层模型、单土层模型a、单土层模型b的桩身弯矩包络图只在泥面下稍有区别，单土层模型b在泥面下弯矩较小，主要是土体弹性模量较大，下部桩身位移较小。

图6 四类模型桩顶位移、桩身最大主应力时程曲线

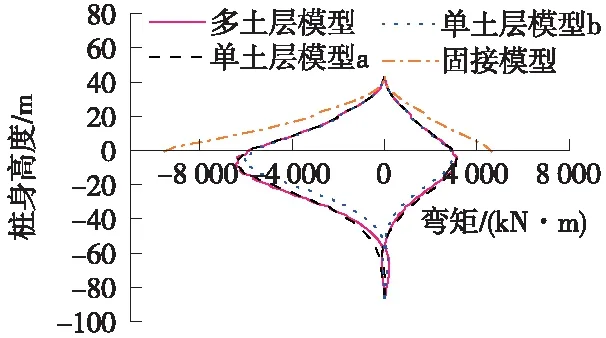
图7 四类模型稳态时桩身弯矩内力包络图

实际上通过对比四类模型，发现多土层模型、单土层模型a响应参量值差异基本在0%～5%以内，即令整个土体等同于多土层情况下的表层土，对单桩水平波流荷载下的响应影响很小，此结论是在表层土占实际桩体埋深约25%时得出的。单土层模型b对比多土层模型相差较多，主要是该实例中第二层土体性质与表层土体差异较大，如弹性模量相差近1倍。固接模型与多土层模型相比其他两类模型结果差异更大，这是因为固接模型以泥面处的固接约束替代实际泥面下的桩-土相互作用，大大增加了横向刚度。

3.2 不同模型稳态响应的统计值差异

令波流荷载波高1.8 m，流速1.0 m/s，计算8个不同周期(5，6，7，8，9，10，11，12 s)工况下四类模型的稳态响应。对稳态时桩顶位移与桩身最大主应力选取至少5个周期的时程数据，得到对应工况下峰值的平均值，并分别作为统计值Ymax和Smax，令图7弯矩包络图的最大弯矩值作为对应工况的桩身最大弯矩统计值Mmax。

如图8所示，不同模型在相同波流荷载下的响应存在一定差异。对比多土层模型结果与固接模型结果，多土层模型桩顶位移约为固接模型的2～3倍，最大主应力约为固接模型的1.3～1.5倍，桩身最大弯矩在固接模型的68%左右。对比前三类模型，多土层模型、单土层模型a的桩顶位移、桩身弯矩及最大主应力相差很小，单土层模型b除了最大主应力(波浪荷载对桩身重力作用平衡下的最大主应力影响较小)，桩顶位移与桩身最大弯矩均同多土层模型、单土层模型a有明显区别。

三类模型中多土层模型模拟实际的土层分布，单土层模型a土体采用表层土体，其中表层粉土土层厚度只占桩基入土深度的24.4%，但是两者结果十分接近，单土层模型b采用的粉砂土层为实际桩基泥面下的第二个土层，厚度占桩基入土深度38.5%，其与多土层模型结果差异较明显，一是因为粉土土层与粉砂土层土体参数差异较大，二是实际情况下粉砂土层在桩基下部较深的位置，对桩基响应的影响相对于表层的粉土土层小。

4 波-流参数的影响

4.1 周期影响

为研究不同波流参数对桩基动力响应的影响，以多土层模型作为研究模型进行不同波流参数的动力响应计算，并以固结模型作为对照。令，波流波高1.8 m，流速0 m/s，周期为5～12 s，计算得到多土层模型与固接模型的稳态响应，并按上节方法得到各参量统计值。图9为两类模型的桩顶最大位移Ymax，桩身最大主应力Smax与桩身最大弯矩内力Mmax随波流周期的变化。可见Ymax，Smax，Mmax三个统计值均随波流周期增加而非线性减小，除了桩身最大弯矩外，多土层模型桩顶位移与桩身最大主应力均大于固接模型。

图9 多土层模型与固接模型响应峰值随周期的变化规律

4.2 流速影响

令，波流周期5 s，波高2.2 m，取流速分别为0，0.5，1.0，1.5 m/s。如图10所示，两类模型的Ymax，Smax，Mmax值在选取的流速范围内结果改变较小，但有先下降后上升的趋势，其中位移增幅在30%以内，应力增幅在25%以内，弯矩增幅在10%以内。

图10 多土层模型与固接模型响应峰值随流速的变化规律

4.3 波高影响

令，波流周期5 s，流速为0，分别取波高2.2，2.6，3.0，3.4，3.8，4.2 m。如图11所示，两类模型的Ymax，Smax，Mmax值几乎都是随波高线性增加。

固接模型与多土层模型的结果对不同参数变化有着相同的规律，Ymax，Smax，Mmax随波流荷载周期的增加而非线性减小，随流速增加先减小后增大，且增幅较小，随波高线性增大。多土层模型除了桩身弯矩远小于固接模型外，其桩顶位移与桩身最大主应力均大于固接模型。

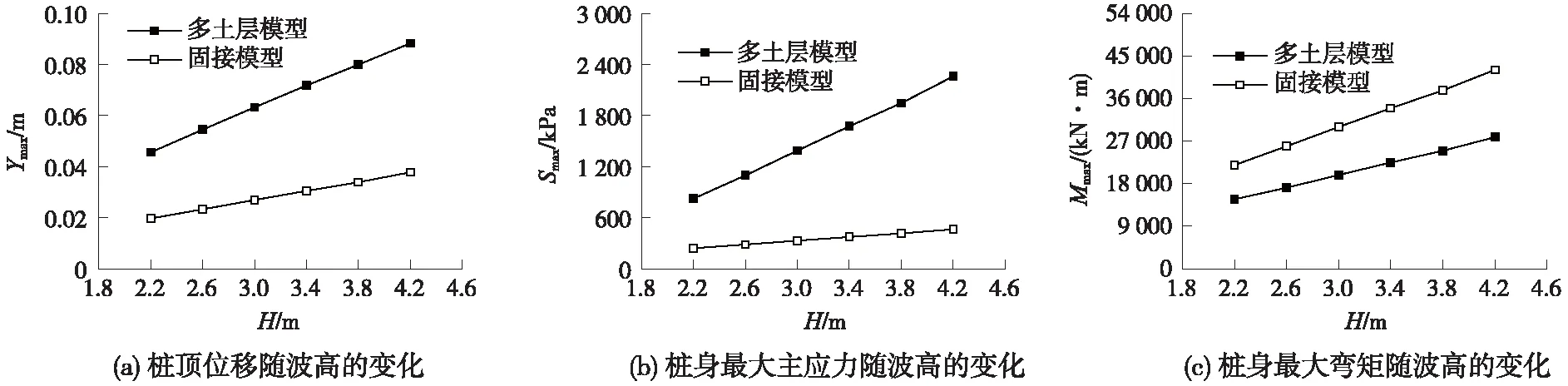
图11 多土层模型与固接模型响应峰值随波高的变化规律

5 群桩效应的影响

相比单桩，群桩效应主要来源于两方面，一方面是上部桩与桩之间相互影响使得波流场改变，导致波流场对每根桩的荷载改变；一方面是下部土体应力状态相比单桩不同，多个桩之间挤压土体产生的应力相互影响与叠加。本文利用Abaqus桩-土接触模型模拟下部土体群桩效应。

5.1 荷载周期与入射角对群桩的影响

本文中群桩基础方案实际相对桩距S/D=2(S为桩心距，D为桩径)，不同波流入射角情况下，不同桩柱上的波流荷载都存在固定相位差[14-15]，利用Matlab编程计算图5布置形式下不同桩上的波流时程荷载。选取0°，15°，30°，45°，60°，75°，90°共7个入射角工况，其中波流荷载周期9 s，波高2.6 m，流速1.0 m/s。图12为两类模型的桩顶承台处位移与桩身最大主应力随入射角的变化曲线。可见两个模型的响应均随入射角增加而增大，多土层模型比固接模型的位移和应力更大。

图12 群桩在两类模型位移、应力随入射角的变化

图13 群桩在两类模型的位移、应力随周期的变化曲线

令入射角为0°，波高2.6 m，流速1.0 m/s，设置5，7，9，11 s四个不同周期的工况。如图13所示，两类模型承台处位移与桩身最大主应力并非随周期单调变化，呈现不规律性，除了有限体积土体模型对整个结构频率的微小影响外，作用在各排桩上的波流力存在相位差异，通过桩顶承台约束，导致整个群桩所受波流力合力并未呈现单桩那样随周期变化的规律。

5.2 波流荷载群桩效应的影响

一般工程计算中未考虑各桩柱对上部波流场的影响，即流场群桩效应。本文的计算忽略承台对上部波流荷载的影响[16]及波流横向力[17]，通过引入群桩效应系数考虑上部群桩效应，并与未考虑上部群桩效应的结果作对比。

对应设置工况下的相对桩距与KC数，参考文献[18-22]关于双桩、三桩串并联的群桩效应系数及九桩串联群桩的实验结果，计算S/D分别为1.5，2，3时各组成桩的群桩效应系数，令波流荷载入射角0°，周期9 s，流速1 m/s，波高2.6 m，表2为相对桩距S/D=2时各组成桩的群桩效应系数。

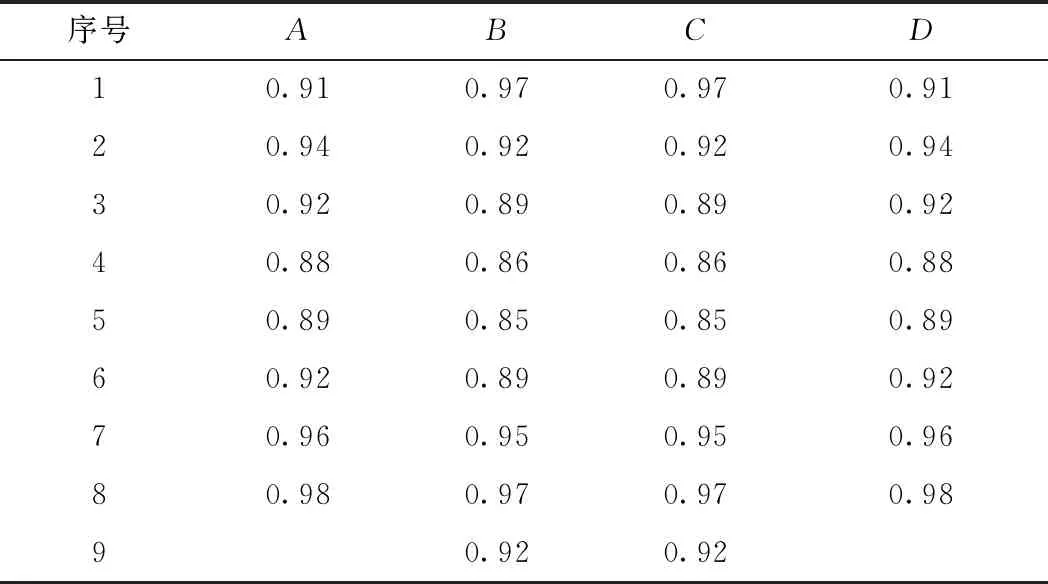
表2 相对桩距S/D=2时各组成桩群桩效应系数

图14为群桩多土层模型与固接模型在考虑上部波流场群桩效应与未考虑群桩效应情况下，承台处位移与桩身最大主应力随桩间距的变化。

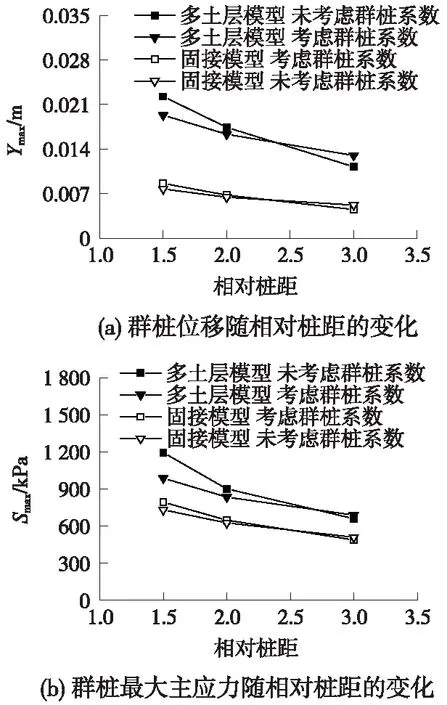
图14 两类群桩模型位移与应力随相对桩距的变化

相对桩距S/D值较小时，桩列对波流的阻塞效应使桩处流速增大，桩顶位移与最大主应力均大于未考虑上部群桩效应的结果，且在S/D=1.5时差异更加明显。而在S/D=3时，考虑上部群桩效应的结果偏小，这是因为组成桩的间距增加，存在前方桩对后方桩的遮蔽效应，使得群桩效应系数小于1，群桩合力小于各单桩上力的叠加。随着相对桩距的增加，组成桩周围的流场更接近独立单桩，群桩效应逐渐减弱，两种响应也逐渐趋同。对比固接模型，群桩效应造成的响应差异，没有多土层模型明显，是因为群桩效应引起的波流荷载大小改变较小，而群桩固接模型刚度较大，相应地响应差异也变小。

6 结论

根据实际工程中的桩基及土层信息建立桩-土相互作用模型，采用Morison方法得到不同参数下的波-流荷载。对比研究了波-流荷载作用下桩基础在不同土层模型的动力响应，以及不同波流荷载工况下单桩与群桩响应随荷载参数的变化，具体结论如下。

(1)波流荷载作用下的单桩动力响应，如桩顶位移、桩身最大主应力与桩身最大弯矩均随波流周期增加而非线性减小；随波流波高增加线性增大；随流速增大先减小后增大，且增幅较小。

(2)单桩多土层模型相比单土层模型，波流荷载下的动力响应差异很小；较深处土层性质对波流荷载下单桩动力响应的影响很小。

(3)群桩位移与应力响应随周期变化规律不同于单桩，本文布置形式的群桩，位移随入射角增加基本呈线性增加，桩身最大主应力先增加后减小。

(4)考虑上部流体群桩效应后得到的响应与未考虑时的响应在相对桩距S/D为1.5或2时前者更大，相对桩间距为3时后者更大。实际群桩施工设计可简化土体性质等同为表层土体，在较小桩间距情况下不可忽略上部流体群桩效应。