基于CFD 的管片式换热器空气侧散热片结构的参数优化∗

陈家浩 邓 斌

（西南交通大学先进驱动节能技术教育部工程研究中心 成都 610031）

1 引言

无论在工程机械或日常生活中，管片式换热器都已经成为研究的重点，尤其对于工程机械，换热器的换热性能直接影响到整车能否正常运转［1］，当换热量不足时，便会引起发动机内部活塞、活塞环和缸套发生咬伤，发动机便会过热，导致充气系数下降，燃烧异常，发动机性能下降［2］，因此提高换热器的换热性能至关重要。

换热器的翅片种类主要包括平直形、锯齿形、波纹形、百叶窗等，并且平直翅片具有低压降的特点［3］，考虑到工程机械的工况比较复杂，为降低采用复杂翅片带来的流道阻塞所带来的不良影响［4］，因此，水箱散热选用的换热器的空气侧翅片主要为平板翅片（如图1 所示），由于水箱的热阻主要集中在空气侧，因此强化空气侧的传热为本文研究的重点［5］。董启军［6］研究了平直翅片的性能和几何参数对性能的影响。由于传统的换热器设计和试验既耗时同时成本也高，相较于试验研究，CFD 技术对压裂车换热器的研究具有明显的优势，不仅可以快速模拟流道内部复杂结构的液体流动和传热特性［1］，同时还可以大幅度节约研制费用并缩短研发周期。

图1 管片式换热器

2 三维几何模型的建立

换热器由冷却水管和散热片组成，整体模型较为复杂，但散热芯体内部的散热片和水管的排列具有周期性和对称性，为加快计算时间，对模型进行了简化处理，简化后的管片式换热器的结构参数如图2所示，其调整结构参数见表1。

图2 管片式换热器简化模型

3 数学模型

3.1 控制方程

假设在换热器中冷却空气的流动为不可压缩定常流动，可知流道内空气的流动及换热的控制微分方程如下［7～10］：

连续性方程：

表1 管片式换热器散热片参数

动量方程：

式中：ρ 为流体密度；ui为流体速度；p 为流体在微元体上的压力；k 为换热系数；μ 为动力粘度；T为温度；Cp为定压比热。

由于模型内部空气为湍流，因此采用standardk-ε 模型［11］

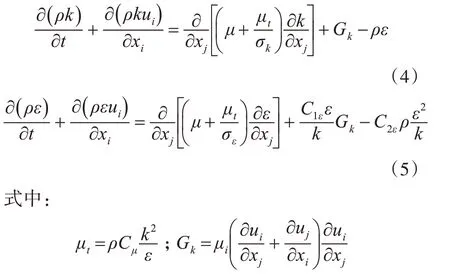
ρ 为空气密度；μ 为黏性系数；μi为湍流黏性系数；k 为湍流动能；ε 为湍流能量耗散率；Gk为紊流动能产生率；σk，σε为湍动能k 和湍动耗散率ε 对应的Prandt1 数，σk=1.0，σε=1.3；Cu，C1ε，C2ε为模型常数，Cu=0.09，C1ε=1.44，C2ε=1.92。

3.2 边界条件设置

将简化后的模型导入Workbench，为减小入口湍流和出口回流的现象，对入口和出口均做了延伸处理［12］，根据Wang［13］的研究，采用周期性边界流体模型进行计算，建立了图3 的流体计算区域。由于计算域较为复杂，因此采用混合网格进行划分，并且在翅片近壁处采用避免函数法进行了处理，总网格数为11 万，节点为4.7 万。流体计算区域、散热片和水流道的网格划分如图4 所示。经网格无关性验证，网格数符合计算精度要求。

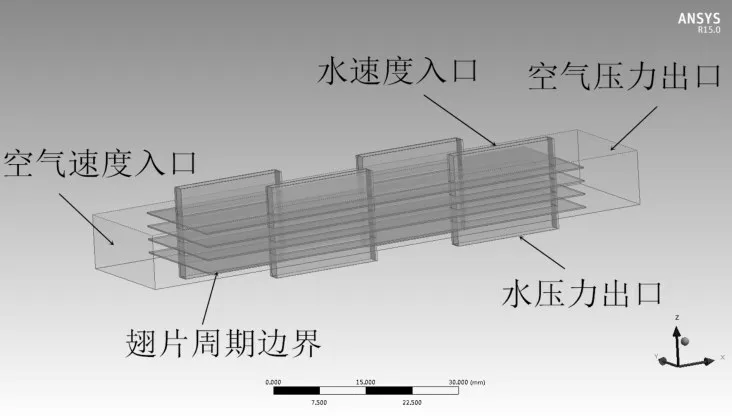
图3 流体计算区域和边界条件

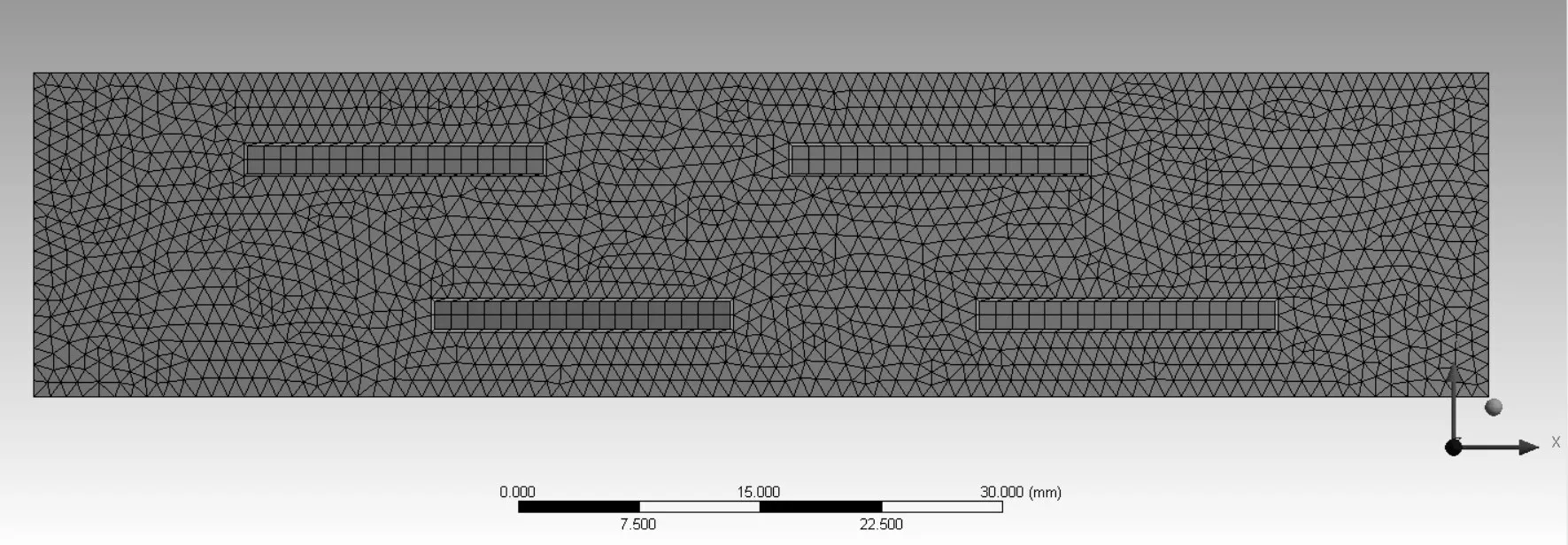
图4 计算区域的网格划分

3.3 数值求解

基于有限体积法的控制方程离散，采用一阶迎风格式，为解决压力场检测问题，运用SIMPLE算法求解［14］，通过数值计算的数据，通过计算得到翅片摩擦因子f和传热因子j，同时还可得出平均努塞尔数----Nu。

传热因子j：

式中：Cp为定压比热；Pr 为普朗特数；μ 为动力粘度；h 为换热系数；u 为空气入口速度；ρ 为空气密度。

摩擦因子f ：

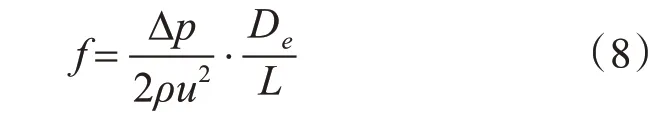
式中：De为水力直径；Δp 为空气侧压降；L 为空气掠过的翅片长度。

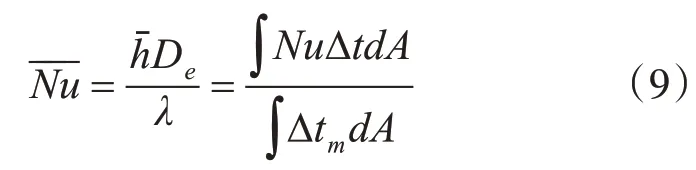
4 仿真结果及结果处理

4.1 仿真结果图像

运用fluent 对空气侧的计算结果进行处理，管片式换热器的仿真结果云图如图5所示。

图5 仿真结果云图

由图5（a）可以看出当空气掠过管道时，气流速度发生了明显下降，但在其他位置时，速度变化范围较小，在靠近中央部分有明显的湍流现象；由图5（b）可知，空气流经水管壁后，温度明显上升；图5（c）中在空气入口处和水流道接触地方压力发生了骤降，并且压力沿空气流动方向逐渐下降。

4.2 结果分析

根据单一变量原则，采用控制变量法和正交试验设计的基本思想［15］，对不同结构尺寸的散热片进行了仿真分析。并将得到的数据运用Matlab 进行进一步的整合，利用插值原理得到平滑的拟合曲线结果如图6所示。

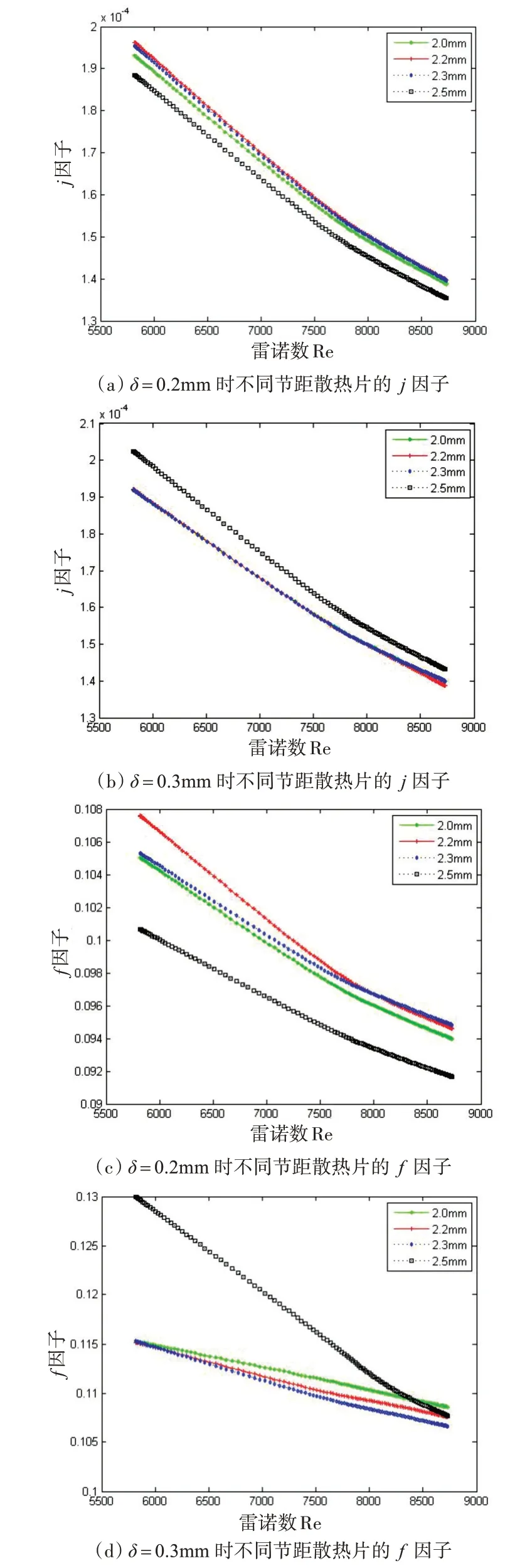
图6 0.2mm和0.3mm散热片厚度下不同节距翅片的j因子和f因子随雷诺数Re的变化

由图6（a）可以看出，当散热片厚度为0.2mm时，不同节距的散热片的j 因子均随着雷诺数的增大而减小，当节距为2.2mm 时，j 因子均为最大，节距为2.5mm时，j 因子则均为最小；由图6（b）可知，散热片厚度在0.3mm 时，不同节距的散热片的j 因子同样随着雷诺数的增大而减小，但和0.2mm厚度的散热片相反，当散热片节距为2.5mm 时，j 因子最大，节距在2.0mm～2.3mm 时，j 因子最小；由图6（c）可以看出，当散热片厚度为0.2mm 时，多种节距的散热片的f 因子随着雷诺数的增大其下降速率几乎一致，节距为2.2mm 时f 因子最大，节距为2.5mm 时f 因子最小；由图6（d）可知，当散热片厚度为0.3mm时，节距为2.0mm～2.3mm的散热片的f因子随雷诺数的增大下降速率较为缓慢，节距为2.5mm的散热片的f 因子的下降速率明显较大，但整体而言2.5mm 节距的散热片的f 因子远高于2.0mm～2.3mm节距的散热片的f 因子。

综合可得，在散热片厚度为0.2mm 和0.3mm时，随着雷诺数的逐渐增加，多种节距散热片的j因子和f 因子均逐渐减小。为进一步得到最优翅片，结合图6（a），（b），（c），（d）中曲线的变化，采用强化传热性能的评价准则常用的j f13作为判定标准［16］，并观察j f13相对于散热片节距的变化。

采用Matlab对进行曲线的绘制，如图7所示。

图7 j f1 3 随散热片节距的变化

由图7 可得，当散热片厚度为0.2mm 时，传热特性明显优于0.3mm 厚度的散热片，j f13随着散热片节距的增加，其值先增大后减小，最大值位于2.25mm 附近，用Matlab 对曲线进行四次多项式差值求解得到式（10），分别对在2.21mm～2.27mm 之间数据代入式（10），结果见表2。

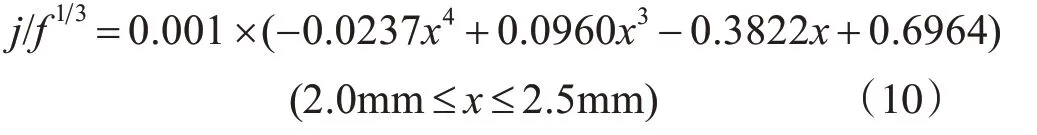
由表2 明显可以看出在节距为2.22 时，j f13取得最大值，散热片综合性能最好。

表2 不同散热片节距的j f1 3 数值

5 结语

通过对空气侧翅片的模拟仿真分析，得到了散热片的传热特性和压降随雷诺数的变化趋势，并且采用CFD 数值模拟方法大大减少了管片式换热器的试验成本，缩短了生产周期，同时对以后的管片式换热器的设计提供了理论依据。

通过Matlab 对曲线的拟合，得到了j f13判定标准的四次多项式，根据函数思想得出了散热片厚度为0.2mm，节距为2.22mm 时，散热片综合性能最佳。