论数学核心素养在高中数学课堂落地生根——以人教版高中“对数”教学为例

邵贵明，胡典顺，柳福祥

论数学核心素养在高中数学课堂落地生根——以人教版高中“对数”教学为例

邵贵明1，2，胡典顺1，柳福祥3

（1．华中师范大学 数学与统计学学院，湖北 武汉 430079；2．黄冈师范学院 数学与统计学院，湖北 黄冈 438000；3．三峡大学 理学院，湖北 宜昌 443002）

课堂教学中提升学生数学核心素养的策略有：数学学科知识是桥梁和媒介；数学思想方法和思维方法是利剑；数学精神和数学文化是助推剂．选取高中数学“对数”教学为例展开教学设计和教学实践，通过课堂实施的4个环节：历史探源—激发动力—发展思维，数据悟律—运算求理—形成概念，模型转换—逻辑推理—生成法则，内化知识—发展能力—交流升华，分步论证揭示数学核心素养的课堂落脚点、生长点和发展点．

数学核心素养；成分分析；落实策略；教学设计

1 问题提出

2014年《教育部关于全面深化课程改革落实立德树人根本任务的意见》明确了核心素养的概念，即学生应具备的适应终身发展和社会发展需要的必备品格和关键能力．之后《普通高中数学课程标准（2017年版）》（以下简称《课标》）为高中数学确定了数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析六大数学核心素养．这些都为中国基础教育数学学科的研究与实践指明了方向．回顾近些年来关于数学素养、数学核心素养的研究，较多地偏重理论，与落实到基础教育实践尚有距离．实际上早有教育研究者呼吁落实的问题．有的在基于文献综述的基础上，提出研究数学素养的4个落脚点，其中强调了要分析数学素养的生成机制和探索数学素养生成的教学策略[1]．有的在梳理中国核心素养的研究进展基础上，提出未来研究工作应关注5个方面，其中也特别关注了两点：分析数学核心素养的生成机制，探索数学核心素养生成的教学策略[2]．后来又有学者分析学科核心素养形成机制时提出：学科知识是学科核心素养形成的主载体，学科活动是学科核心素养形成的主路径[3]．但依然是未能在课堂落地生根．

可见明晰数学素养、数学核心素养的内涵与构成要素，将数学核心素养的研究植根于基础教育实际是非常必要的．因此，一方面必须深度剖析其内涵及构成要素，解决具体落实什么的问题，另一方面必须探讨落实策略，结合具体的教学情境、教学内容解决如何落实的问题．从而体现探究出数学核心素养在课堂的落脚点、生长点和发展点的一般规律．

2 数学核心素养的发展历程及成份的认识

要想让数学核心素养落地生根，必须理解并认识核心素养的本质，挖掘其构成要素，目前有数学思想方法说、思维说、能力说等．为了进一步认识，就要从源头来认识核心素养的成分，才能明确中学课堂教学中数学核心素养形成机理的核心要素．

2.1 数学核心素养的起源及发展

数学核心素养概念的提出经历了一个不断发展的过程．若追溯其源头得从素养说起，最早研究素养的世界权威机构是经济合作与发展组织（OECD）．1997年底，OECD和瑞士联邦统计署（SFSO）赞助了一个国际性的跨界合作项目，即“素养的界定与选择：理论和概念的基础（DeSeCo）”．该项目由社会学家、评价专家、哲学家、人类学家、心理学家、经济学家、历史学家、统计学家、教育学家以及决策者、政策分析师、贸易联盟、雇主、全国性和国际性组织代表共21人组成，分别出版了关于核心素养的系列研究报告．如2001年出版论文集《确定与选择核心素养》，2003年发表项目最终报告《指向成功生活和健全社会的核心素养》，以及2005年发表《核心素养的确定与选择：执行概要》．OECD认为素养是运用知识、技能和态度满足特定情境中复杂需要的能力[4]．这个界定将素养的落脚点归结在能力要素上．另外，由OECD主持的国际学生评价项目PISA主要用于测试中学生基本能力．PISA 2012数学素养的标准定义如下：数学素养是个人在不同情境下形成、应用和阐释数学的能力．它包括数学推理能力和使用数学概念、过程、事实和工具来描述、阐释以及预测现象的能力．它有助于个体作为一个关心社会、善于思考的建设性公民，识别数学在世界中所起的作用并做出有根据的数学判断和决定．

中国数学教育界高度关注并发展了数学核心素养，2000年在初高中数学教学大纲中，将思维能力、运算能力、空间想象能力、解决实际问题的能力、创新意识、良好的个性品质和辩证唯物主义观点纳入数学素养的范畴．其主力军仍然是中国传统意义上的三大能力．2002年在高中数学教学大纲中继续提到“使学生在高中阶段继续受到教育，提高数学素养”，依然强调了三大能力，且内容更加丰富，加入了直觉猜想、归纳抽象、符号表示、演绎证明，更强调了数学思维能力．接下来中国在新一轮课程改革的课程标准中也着重强调了数学核心词．直到以林崇德先生为首的核心素养课题组确立“中国学生发展核心素养”：以培养“全面发展的人”为核心，分为文化基础、自主发展、社会参与3个方面，综合表现为人文底蕴、科学精神、学会学习、健康生活、责任担当、实践创新六大素养．其涉及范畴的实质也是一种从内修到应用、从基础到发展意义上的能力．

2.2 数学核心素养成分构建的认识

《课标》确定了数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析六大数学核心素养．教育研究者也曾对数学核心素养的成份构建进行了深入探讨．蔡金法、徐斌艳从人才观、数学观（学科观）论述了数学核心素养的构建分为数学交流、数学建模、智能计算思维和数学情感4个方面[5]；李星云构建了数学交流、数学推理、运算能力、空间观念、数据分析能力和数学建模6个方面[6]；何小亚在数学核心素养指标之反思中又提出了数学化、数学运算、数学推理、数学意识、数学思想方法和数学情感态度价值观六大框架[7]．

这些研究普遍认为数学推理、数学抽象、数学运算是数学核心素养最重要的部分，并从不同的视角剖析了数学核心素养的成份构建，各有千秋．不同的是各自的分类和侧重点略有差异，主要表现在以下4个方面．第一，对数学推理表述的侧重点不同．蔡金法等则模糊了数学推理的界限，将数学推理内渗于数学交流与数学建模中．《课标》把数学推理明确为逻辑推理，将直觉思维下的合情推理及猜想归入直观想象中，显得语言更简洁、脉络更清晰．第二，数学抽象对应的归类不同．何小亚采用过程化处理方式将数学抽象和数学建模归到数学化一类中，但是数学化对于中学教师而言是一个较模糊的概念，不利于分清层次．《课标》的表述显得实践指导性更强．第三，成份的内涵表述不同．《课标》在数学运算的具体表示中强调运算法则、演绎推理、数理逻辑．蔡金法、徐斌艳突出强调了数学智能计算思维，这是对数学运算内容的时代性丰富．第四，关于数学交流．有些学者将之作为成份之一并单列出来．事实上，数学交流存在于一切数学活动之中，数学推理、数学抽象，甚至数学计算也是一种数学交流形式．从某种意义上来说把数学交流看成是一种素质内隐的活动或许更好．此外，喻平通过因素分析、聚类分析得出六大核心素养本质上均为能力[8]．

3 落实数学核心素养的教学策略

目前有部分学者研究了有关数学核心素养落实到中学实践的问题．例如常磊、鲍建生分析论述了在情景视角下落实核心素养的策略[8]．史宁中在“学科核心素养的培养与教学”一文中论述了“用数学的眼睛看”落实数学抽象，“用数学的思维想”落实逻辑推理，“用数学的语言说”落实数学模型[9]．章建跃、程海奎以概率课程为例，宋运明以勾股定理内容为例，主要从编写教材的角度谈如何落地[10-11]．吕传汉提出教思考、教体验、教表达（简称“三教”）的教育理念，尝试用“三教”引领“创设数学情境与提出数学问题”培育学生核心素养[12]．这些研究主要还是基于理念探讨的层面，仍缺乏具体的指导性和可操作性．

要想让数学核心素养在中学课堂落地生根，根据以上分析，提升学生的能力和关键品格是主抓手．克鲁杰茨基曾经说，只有在分析特定活动的基础上才能揭示能力，并在实验和实践的基础上提出了能力的12成份说．但根据中国的国情和习惯，数学能力分为一般能力和三大特殊能力．一般能力是指观察力、注意力、记忆力．数学特殊能力是指逻辑推理能力、空间想象能力、数学运算能力．提升能力必然要在教学活动中展开，而实际教学活动教师教什么是问题的关键．教学是以数学学科知识为媒介，教给学生数学思想方法和思维能力，引导学生领悟数学精神和感悟数学文化魅力的一种复杂活动．数学核心素养是一切能力中最核心、最关键的能力．它不是孤立的，而是融合在教学活动中的．因此，在提升学生数学核心素养过程中，落实策略为：数学学科知识是桥梁和媒介，数学思想方法和思维方法是利剑，数学精神和数学文化是助推剂．

鉴于目前丰富多彩的以说理为主的研究操作性不强，特此以课例为支点展开研究．首先剖析学科知识的内容和结构，发挥其桥梁和媒介作用，展开教学活动．整个教学活动中数学思想方法和思维方法就像一把利剑，把各个核心素养串连起来，各个击破．同时数学学科精神和数学文化为数学课堂增加了哲学意蕴和人文关怀，有助于提升学生的数学核心素养．中学数学课堂活动围绕上述线路展开，期望为研究者和一线教师提供借鉴．

4 基于数学核心素养的教学过程呈现

选用人教版高中数学必修1的“对数”教学为例，基于核心素养为课堂教学的落脚点、生长点和发展点，进行教学设计和实践探索．选用该课例的原因是学生对于这节课普遍认为抽象、难以理解．现实教学中新授课后，仍然有相当数量的学生在计算上会犯“积的对数等于对数的积”这样的错误．基于落实核心素养的理念来换角度设计并实施教学，从考虑对数相应的数量及数量关系入手，兼顾数学的历史发生原理，即当学生学习遇到障碍的时候，反思历史上数学家们是不是也曾遇到这样的困惑，将数学精神和数学文化作为助推剂．

事实上，1614年苏格兰数学家纳皮尔（J. Napier，1550—1617）出版了《奇妙的对数定律说明书》，他被认为是对数的发明者．从那时到1728年瑞士的大数学家欧拉（L. Euler，1707—1783）理顺指数与对数的关系：对数源于指数．“对数”这个概念经历了一百多年才真正为人们所接受．要想顷刻间让学生接受对数的概念和运算法则这个事实是相当困难的．尽管教材后面也有“对数的发明”的阅读材料，只可惜不足以引起师生们的重视．因此基于数学核心素养的视角进行重新设计“对数”的教学是必要的．另外，落实到具体的某节课，并非一次性将六大核心素养都体现出来．在“对数”这节课中，主要考察数学抽象、逻辑推理、数学运算和直观想象、数学模型5个方面．这里按照教学流程展示其中部分细节．

4.1 历史探源 激发动力 发展思维

基于落实核心素养的培养方案，以数学史和数学文化的视角导入课题，深度激发学生的探究欲望，教学中发挥数学思想方法和思维方法的利剑作用．简要经历对数发明的历程，让学生在数学抽象的过程中，经历感受并体验纳皮尔发现对数的思维活动，在运算结构由浅入深的过程中提升运算能力、逻辑推理能力．以下为部分教学设计．

教师通过生动讲解，导入如下内容：自古以来人们都在追求长寿的秘诀，有一位数学家发明了一种神奇的运算，成倍地延长了科学家和工程技术人员的寿命，大家知道是谁吗？（停顿）他就是苏格兰数学家纳皮尔．纳皮尔是位神奇的人物，每次在公众场合出场都带着他的宠物蜘蛛和公鸡，他在1594—1614年间花了人生宝贵的20年打造了第一个神奇的对数表，这种对数的方法化乘除为加减，化乘方开方运算为乘除运算，大大缩减了繁杂冗长的运算．恩格斯将之比喻为数学科学的最有力的杠杆之一[13]．这个有力的杠杆是怎样工作的呢？事实上，纳皮尔也是以阿基米德等前人的工作为基础的．

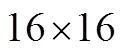
目前，全国有84689个城市社区、59.9万个建制村（社区），共有社区居委会成员43.1万人、村民委员会成员234万人，社区公共服务从业人员215.8万人，社区志愿者2900多万人，还有一批具备专业知识的兼职工作人员进入社区工作，城乡社区服务事业取得了显著成就[2]。但是随着工业化、信息化、城镇化、农业现代化、市场化、国际化的进程逐步加快，我国城乡社区服务体系建设仍然处于初级阶段，存在许多困难和问题，也面临许多机遇和挑战。

学生跟随老师一起运算，通过比较，初步感受用加法处理乘法之运算简便的神奇功效．为后面进行由数列到函数的类比过渡，为概念的数学抽象做准备．接着教师引导分析，为了更清楚地反应这样的对应关系，不妨用函数来表示这样的两个数列中数的关系．同时将正整数扩充到整数、甚至实数，继续来观察表2．

表1 双数列的对应关系

表2 两数列对应的函数关系

在表2中，下栏和上栏两变量之间的关系为指数函数关系：=2，在对下栏的数做加法的基础上继续验证做减法、乘法、乘方运算，可以得到对应等比数列中的数作除法、乘方、开方运算．（引导学生检验）

4.2 数据悟律 运算求理 形成概念

学生在检验另外3种运算中体验了计算的强大和简便，对应关系的巧妙．通过检验从数量关系中逐步过渡到抽象出函数关系，建立指数函数和对数函数模型．

在这个落实初步数学运算核心素养的基本过程中，教师引导学生从简单到复杂的过程中，理解运算对象、掌握运算法则、探究运算方向、寻求运算结果，从数据的比较分析中探知对应关系的规律．

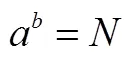
图1 指数式和对数式中各要素的对应关系

学生仔细观察领悟，根据表2和这个互逆运算图，感受数学抽象概念——对数的诞生，逐步明白对数的“对”的本质是“对应”，体会运用数学运算的法则，用对应关系进行数学概念下定义的方法．课堂由运算悟律过渡到概念生成．

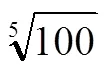
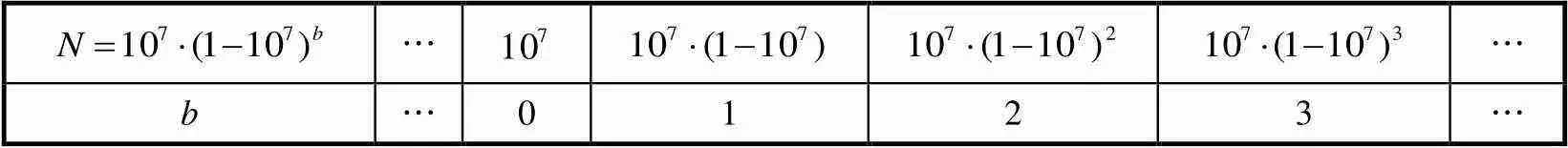
表3 纳皮尔创造的对应关系

学生跟随教师的引导，一步步地进行数学抽象，建立底数不同的对数模型，逐步过渡到一般化问题，兴趣盎然地感受数学的魅力，逐步形成类似数学家的乐于探究的趋同感．教师指出，直到1728年瑞士的大数学家欧拉才理顺指数与对数的关系，他认为对数源于指数，从指数式的数量关系中可以突出互逆运算的特征．引导学生训练并熟练掌握指数、对数互化，加深认识对数符号和概念本质，为后续探究运算法则作铺垫．接下来进行课堂演练指数式、对数式互化．

4.3 模型转换 逻辑推理 生成法则

对于教师引导学生猜想对数的运算会有哪些规则这个问题，在一个示范高中教学实践中，发现一部分学生按照从指数类比到对数来推导对数运算法则，即以对数来源于指数运算的性质为逻辑推理的基础（虽然历史上，对数的概念发展先于指数函数）．事实上，对于指数、对数式互化的关系，大部分学生还只是停留在建立概念的需要，并不能深入到应用其推导法则．教师仍要激发学生用比较与类比的思想来思考，才能培养学生数学核心素养之逻辑推理素养，可以采用如下引导语：既然对数概念是从指数式与对数式互化得出的，那么类比指数运算性质是否能得到对数运算法则？学生逐条写出指数运算性质，反复比较依据指数与对数的转换关系进行推理，将指数式换成有算理意义的对数式，试图就得出对数的运算法则．

课堂表现为教师呈现表格（见表4），学生提笔耐心计算逐一填表．师生共同获得结论，领悟核心素养的内涵之逻辑推理与数学运算之间的关联，领悟指数模型、对数模型对运算的贡献．

表4 对数运算思维过程

数学的运算法则也就是在这种逻辑推理的思维过程中顺理成章地生成的，符合课程标准制定组的导向，将数学核心素养有心处理落实到无意教学中．同时在经历用类比思想、化归思想做数学的过程中，夯实基本知识、掌握基本技能，培养了分析问题、解决问题的能力．

4.4 内化知识发展能力交流升华

实践教学中另一部分学生却是按照下列方式来思考的．师生通过直观、类比想象实数的加减乘除运算法则，考虑既然对数也是数，通过实数类比对数的运算法则，即能否确定两个对数的和差积商的运算关系？

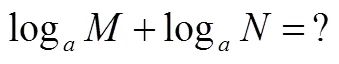
5 结语

为了进一步落实数学核心素养到基础教育的实践，追溯数学核心素养的发展历程，梳理了国内外的相关研究，得出数学核心素养侧重于能力层面．针对数学学科的特点和数学的本质展开了探索，探究数学核心素养在课堂教学中的依存方式，认为在提升学生数学核心素养过程中，数学学科知识是桥梁和媒介，数学思想方法和思维方法是利剑，数学精神和数学文化是助推剂．立足于高中数学课堂实践基础，选择普通高中概念教学的难点“对数”，进行具体的教学设计并实施教学检验，获得了较好的实验效果．今后为了进一步验证核心素养落实到课堂实践的一般规律，还可以从命题教学、问题解决等方面选取不同的题材进行再探究，探索数学核心素养的课堂落脚点、生成点、发展点，为高中数学教学设计和实施开辟基于数学核心素养落地生根的一般规律，力求从教育理论研究走向教学实践提供更丰富的范例和启示作用．

[1] 胡典顺．数学素养研究综述[J]．课程·教材·教法，2010，30（12）：50-53．

[2] 刘祖希．我国数学核心素养研究进展——从数学素养到数学核心词再到数学核心素养[J]．中小学教材教学，2016（7）：35-39．

[3] 余文森．论学科核心素养形成机制[J]．课程·教材·教法，2018，38（1）：4-11．

[4] The definition and selection of key competencies: Executive summary [EB/OL]. (2005-05-27) [2018-12-18]. http:// www.oecd.org/pisa/35070367.pdf.

[5] 蔡金法，徐斌艳．也论数学核心素养及其构建[J]．全球教育展望，2016，25（11）：6-10．

[6] 李星云．论小学数学核心素养的构建[J]．课程·教材·教法，2016，36（5）：72-78．

[7] 何小亚．数学核心素养指标之反思[J]．中学数学研究，2016（7）：1-3．

[8] 常磊，鲍建生．情境视角下的数学核心素养[J]．数学教育学报，2017，26（4）：24-28．

[9] 史宁中．学科核心素养的培养与教学[J]．中小学管理，2017（1）：35-37．

[10] 章建跃，程海奎．高中必修课程中概率的教材设计和教学思考——兼谈“数学核心素养如何落地”[J]．课程·教材·教法，2017，37（5）：27-33．

[11] 宋运明．中国初中数学教材中勾股定理内容编写特点研究[J]．数学教育学报，2017，26（3）：44-48．

[12] 严虹，游泰杰，吕传汉．对数学教学中“教思考教体验教表达”的认识与思考[J]．数学教育学报，2017，26（5）：26-30．

[13] 李大潜．漫话e [M]．北京：高等教育出版社，2013：2-23．

A Case Study on Rooting the Mathematics Core Competencies in High School Mathematics Teaching——An Example of the “Logarithm” Teaching in the High School

SHAO Gui-ming1, 2, HU Dian-shun1, LiuFu-xiang3

(1. College of Mathematics and Statistic, Central China Normal University, Hubei Wuhan 430079, China;2. College of Mathematics and Statistic, Huanggang Normal University, Hubei Huanggang 438000, China;3. College of Science, China Three Gorges University, Hubei Yichang 443002, China)

The study focuses on the strategies to improve students’ mathematics core competencies in classroom teaching: mathematics subject knowledge is the bridge and medium; mathematics thinking method and thinking ability are the sword; mathematical spirit and mathematical culture are the booster. Selecting the “logarithm” as an example of teaching practice, the authors divide the teaching process into four parts: exploring the historical source-stimulating motivation-developing thinking; understanding the law of data-reasoning from arithmetic-forming the concept; doing the model transformation-logic reasoning-rule generation; and internalizing knowledge-developing capability-communication and sublimation. Through step-by-step argumentation, this study also reveals the foothold, rooting point and development point at which teachers can improve students’ mathematics core competencies in their class teaching.

mathematics core competencies; component analysis; strategy implementation; teaching design

G632.0

A

1004-9894（2020）06-0046-05

邵贵明，胡典顺，柳福祥．论数学核心素养在高中数学课堂落地生根——以人教版高中“对数”教学为例[J]．数学教育学报，2020，29（6）：46-50．

2020-06-20

教育部人文社会科学研究规划基金项目——中小学核心素养测评的模型建构与实证研究（19YJA880012）；黄冈师范学院数学应用与信息处理训练中心项目——“翻”出课堂，“转”出精彩（SXZX201810）；中央高校基本科研业务费专项资金资助——基于学习分析技术的高中数学核心素养评价模型研究（CCNU19TS029）；中央高校基本科研业务费项目——教师教育专项（CCNUTE2020-04）

邵贵明（1973—），女，湖北鄂州人，副教授，硕士生导师，博士生，主要从事数学课程与教学论研究．

[责任编校：周学智、陈汉君]