核心素养视角下云南高中学业水平考试和高考数学试卷分析

李 爽杨泽恒王彭德

核心素养视角下云南高中学业水平考试和高考数学试卷分析

李 爽1，2，杨泽恒1，王彭德1

（1．大理大学 数学与计算机学院，云南 大理 671003；2．郑州枫杨外国语学校，河南 郑州 450000）

在数学核心素养评价框架及指标体系框架下，建立高中数学核心素养评价指标体系，分别对2012年、2018年全国高考文理科数学Ⅲ卷和云南高中学业水平考试数学上半年卷共6份试卷，进行数学核心素养指标标记．对比分析试卷中各数学核心素养及水平的分布，获得如下结论：2012年考卷与2018年考卷对数学核心素养的考查情况总体变化不大；高考和学考、理科和文科试卷对6个数学核心素养的考查权重分布基本一致，权重从大到小依次为数学运算、逻辑推理、直观想象、数学抽象、数学建模、数据分析，与它们之间的内在关系和在整体中的地位是一致的；高考和学考对3个水平的考查权重有较大差异．

数学核心素养；核心素养测评；高考数学试卷；学业水平数学试卷

1 问题提出

2018年1月出台的《普通高中数学课程标准》（2017年版）[1]强调学科核心素养是育人价值的集中体现，是学生通过学科学习而逐步形成的正确价值观念、必备品格和关键能力，并明确数学核心素养包括数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析6个成分．至此，一直讨论不断的数学学科核心素养内涵和整体框架有了正式的表述．如何评价和实践学生数学核心素养的发展，成为需要更加关注的问题．数学核心素养的评价对教学实践中发展学生数学核心素养有重要的引领作用．许多研究者在论述数学核心素养时，都谈到数学核心素养评价的重要性，需要制定科学的评价体系．

目前，数学核心素养评价的研究主要集中在具体的测评研究．国际上关于数学素养测评较有影响的是PISA数学测试．PISA数学测试的研究多集中在测评的内容、测评特点、测评维度、测评框架、测评结果及不同地区结果的比较、PISA数学测试与各国大型数学测评的比较，也有借鉴PISA数学测试框架，进行测试题的设计研究．徐斌艳与蔡金法在文[2]介绍了PISA对美国、德国等国家教育改革的影响，并对美国、芬兰、德国与新加坡4国数学素养的内涵、测评形式和功能等方面进行了比较分析，通过具体实例介绍了数学交流素养和数学情感素养的测评工具和方法，对如何开展包括情感态度和意志品质的数学素养全面测评有很好的借鉴意义．胡典顺、雷沛瑶和刘婷[3]在分析PISA数学素养测试框架的基础上，探讨测试题设计的原则和实践．

国内数学核心素养测评的研究多集中在数学核心素养测评体系的建立和测评的实施、中高考试题蕴含的数学核心素养．喻平在文[4]参照布卢姆模型、PISA模型和SOLO模型，从知识的3种形态（知识理解、知识迁移、知识创新）出发，将数学核心素养划分为3级水平，建立了数学核心素养评价的一个理论框架．之后，喻平在文[5]进一步对6个数学核心素养在3级水平上的具体表现给出操作性定义，建立了数学核心素养评价指标框架．朱先东与吴增生在文[6]中，结合初中知识载体，进一步细化喻平提出的数学核心素养评价指标框架，并对2017年浙江省10份中考试题进行数据分析，提出今后以核心素养为导向的中考命题改革方向，这是目前见到第一篇应用喻平数学核心素养评价指标框架对试卷进行的系统分析研究．

张惠英与王瑞霖在文[7]对2017年河北省中考主观试题6个数学核心素养的考查分布情况、典型题数学核心素养的考查方式、学生的薄弱环节进行了研究，提出有针对性建议；何萍与章才岔在文[8]采用类似文[7]中的方法和方式对温州市2017年中考数学试题进行分析；张斌与苟斌娥在文[9]分析了重庆市2018年中考数学试题（A卷）主观题关于《义务教育数学课程标准（2011年版）》数学素养10个核心概念的考查情况和学生典型错误，从7个方面提出基于考情研究的教学改进策略；但3篇论文都缺乏系统测评框架的建立和框架下的测评．李作滨在文[10]基于《普通高中数学课程标准（2017年版）》对数学学科核心素养的界定和水平划分，参考喻平的“核心素养评价框架”[4]，对每个数学核心素养成分，选择考题进行考查分析，并分析各数学核心素养在试卷中的分布情况，从创新、“四基、四能”、数学核心素养的综合考查等方面分析了试卷的特色，对高考数学命题和教学提出建议．之后，李作滨在文[11]中再次基于课标数学学科核心素养水平划分，对2018年13套高考数学试卷的数学核心素养考查类型和水平进行编码分析．但两文都缺失明晰的“核心素养评价指标框架”下的系统分析．

彭艳贵和徐伟在文[12]中从微观刻画（知识准确性、方向正确性、方法合理性和推理有效性）、宏观描述（数学知识、问题情境和数学思维）和素养水平提升3个方面构建关于高中生数学核心素养测评的三维立体框架，并给出测评流程，但还没有具体的测评实验，其框架和流程需在具体实践中细化和明确．徐柱柱、张迪和綦春霞在文[13]中，从内容维度、认知维度、情境维度3个方面建立了较为完整的数学素养测评框架，并在此框架下通过设计数学试卷对北京某区八年级抽样学生进行测试，分析测试结果，获得学生数学素养整体情况．该文是目前见到的关于数学素养测评有系统测评框架、测试卷设计、具体测试，并依据IRT技术和统计方法分析测试结果很好的实证研究文章，其中关于认知维度的三大能力是阶梯性的，与喻平数学核心素养3级水平有一定的对应，其确定的数学素养仅有5个方面，缺少数学抽象，对数学素养也没有明确的水平划分，缺失对数学素养及水平在测试卷中的分布情况及学生实际达到水平情况的分析．

国内还有一些研究从课程改革、高考改革的角度出发分析学科核心素养评价的背景及意义，阐述高考数学核心素养的评价策略[14]．

喻平建立的数学核心素养评价指标框架有较好的理论基础和依据，有一定的可操作性，但需要通过不断的实践加以完善．高中学业水平考试与高考是两种不同要求的考试，对应《普通高中数学课程标准》（2017年版）数学核心素养的高中毕业水平和高考水平，从喻平的数学核心素养评价指标框架角度，这两种考试关于数学核心素养的考查情况如何？2018年是《普通高中数学课程标准》（2017年版）明确数学核心素养内涵的第一年，间隔5年之前的2012年，虽然已有许多学者讨论数学素养，但对数学核心素养及其6个成分并没有明确的研究．而数学核心素养隐于解题的全过程，强调数学核心素养之后的2018年的高考和学业水平考试与间隔5年的2012年的高考和学业水平考试在数学核心素养的考查方面是否有明显差异？基于这些问题，依据喻平的数学核心素养评价指标框架，借鉴文[6]指标体系，建立高中数学核心素养评价指标体系，分别对2012年、2018年全国高考文理科数学Ⅲ卷和云南高中学业水平考试数学上半年卷，共6份试卷进行分析．为讨论方便，分别记2012年高考理科、文科数学试卷为卷1、卷2，2018年高考理科、文科数学试卷为卷3、卷4，2012年和2018年云南省上半年学业考试（简称学考）卷分别为卷5、卷6．

2 研究设计

2.1 数学核心素养评价指标体系的建立

在喻平数学核心素养评价框架[4]和指标框架[5]，以及朱先东与吴增生数学核心素养评价指标体系[6]的基础上，结合高中数学知识载体，建立高中数学核心素养评价指标体系，见表1．

表1 数学核心素养评价指标体系

2.2 指标值标定原则及示例分析

根据上述评价指标体系的具体操作性定义，为6份试卷所有试题标定数学核心素养类型和水平，并采用分值标记法对每个数学核心素养水平指标进行赋值．由于赋值是对每个题的分值进行划分，标记指标值的过程需遵循如下原则．

2.2.1 素养从重到轻、数量限定原则

高考数学多数试题具有综合性，各素养内涵之间具有交叉性，经常会出现一个题目同时考查多个素养的情况，但往往都侧重考查一个或两个素养，其它素养伴随出现，各素养之间重要程度不同；数学运算和逻辑推理是数学的基础性素养和基本技能，题目几乎都涉及数学运算和逻辑推理．为保证指标值为整数且能体现各素养的主次关系，在标记过程中遵循从重到轻、数量限定原则，对简单、少量的数学运算和逻辑推理不进行标记，优先标记其它素养，从重到轻，同一道题标记指标数量不超过3个．

2.2.2 水平就高不就低原则

数学核心素养的“知识理解、知识迁移和知识创新”3个水平之间具有层次性，后一水平建立在前一水平之上．如果一道题目同一数学核心素养涉及不同水平，则在标记过程中，遵循水平就高不就低原则，同一素养只标记最高水平．以下以3个试题为例，进行指标值标定说明．

（2018年高考理科数学全国卷Ⅲ卷第3题）如图，中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（ ）．

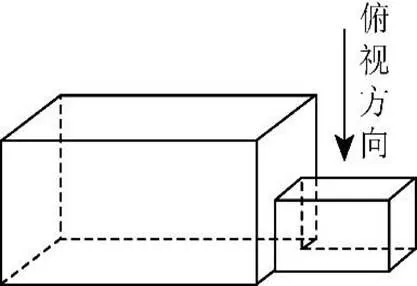
该试题主要考查简单几何体组合后的三视图以及学生通过阅读从具体情境中获取信息的能力，学生需要从文字描述及图形中抽象出咬合和卯眼等概念，还需要在长方体几何特征的基础上，由三视图的特征和刻画要求选出正确答案．主要考查数学抽象素养的第一水平和直观想象素养的第二水平，因此标记对应指标为A1和I2．抽象需要依赖于对图形的理解和想象，因此主要考查的还是直观想象能力．题目分值共5分，数学抽象第一水平赋值2分，直观想象第二水平赋值3分，标定此题目指标值为A1-2，I2-3．

（2018年高考理科数学全国卷Ⅲ卷第5题）若某群体中的成员只用现金支付的概率为0.45，既用现金支付也用非现金支付的概率为0.15，则不用现金支付的概率为（ ）．

A．0.3 B．0.4 C．0.6 D．0.7

该题目是概率问题，同时“现金支付”“既用现金支付也用非现金支付”和“不用现金支付”之间存在逻辑分类关系．题目共5分，在解题过程中，用到概率的基本知识和简单逻辑关系，都是第一水平．而逻辑关系是解答本题目的关键，因此确定此题的指标值为D1-2，R1-3．

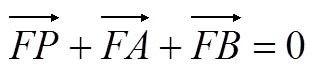
此题综合考查圆锥曲线与向量的基本知识和方法．第（1）题共6分，解题过程中需要理解并熟练运用直线方程、直线与椭圆相交、韦达定理、中点坐标等知识，并迁移到新的数学情境中，通过数形结合进行探究，需要综合运用已学的知识和性质进行探究、推理和计算，但所用的是平面解析几何中常用技巧和方法，故只达到知识迁移水平而非知识创新水平，确定该题的指标值为I2-2，C2-2，R2-2．

第（2）题与上一问相比，需要从题目给出的关系式中挖掘与焦半径相关隐含条件，抽象出数量关系和问题本质，抽象出的条件及关系是解题中常用的坐标间数量关系，属于知识迁移水平而未达到创新水平．在解题过程中，需要探究并综合应用知识和方法进行计算和推理，属于知识创新水平．各素养之间相辅相成，没有明显的主次之分．因此，确定该题的指标值为A2-2，C3-2，R3-2（总分6分）．

3 研究结果

3.1 6份试卷数学核心素养情况

3.1.1 各试卷数学核心素养及水平分布

依据上述标记方法和原则，对6份试卷的所有题目进行指标值标定，得到每一份试卷的数学核心素养及水平分布表．表2给出2012年高考理科数学试卷的数学核心素养及水平分布．试卷中指标的权重值，是通过计算该指标的总分值占试卷总分值的百分比确定的．每个核心素养的总权重值是该素养3个水平权重值的和．试卷中选做题的权重，需要乘以该题被选中的概率，例如2012年理科高考试卷选做题是在3道选做题中选择1个题目，每个题目的核心素养指标值需要乘以1/3．从17题开始，每题有2问．

3.1.2 6份试卷数学核心素养分布汇总

6份试卷数学核心素养分布汇总如表3所示．

3.2 核心素养权重统计分析

3.2.1 不同素养权重分析

数学运算总体平均权重最大，这基于两个主要原因：一是由于数学问题的解决很大程度上依赖于运算，特别是在试卷的大题部分，每道题目都会涉及大量且复杂的运算，数学运算贯穿全份试卷．二是在试卷基本题部分，存在个别题目仅使用单一的公式和法则进行运算，即只考查了数学运算素养．充分体现数学运算是最基本、最重要的数学核心素养．如果数学运算素养水平低，其它素养的发展也会受到影响，传统的双基训练中，数学运算的训练一直都是重点．

表2 2012年高考理科数学试卷数学核心素养及水平分布

数据分析的总体平均权重最小，这源于考查数据分析素养的题目只出现在概率模型和统计知识题目中，解题过程都还包含有其它素养成分，而其它素养的考查题目都不涉及数据分析．相对2012年高考卷，2018年高考卷增大了数据分析素养的考查权重，6份试卷考查数据分析的20道题目中，有13道小题和4道大题都有实际背景，这源于数据时代，普通人将面临更多数据分析的现实情景，对数据分析素养的要求不断增高．随着更多中国学生参加2012PISA数学测试，学生应对现实情景的数据分析等素养更加受到重视，2018年高考卷体现了这一点．

数学建模总体权重平均值为10.83%，相比之下权重较小．数学建模素养和数学抽象素养关系密切，但其权重却远低于数学抽象所占权重．数学建模包含抽象的过程，而在高中数学知识的背景下，数学抽象的体现形式比数学建模更多样，许多非数学建模问题中也包含数学抽象素养，而数学建模素养只出现在有实际背景的应用问题中，因而，数学建模权重比数学抽象小．

数学抽象、逻辑推理和几何直观总体权重平均值分别为16.04%、18.24%和17.76%，所占权重相近且适中．每份试卷对6个素养的考查情况均体现数学运算权重最大，数据分析素养和数学建模素养权重较小，其余3个素养权重相近．

3.2.2 同一素养不同水平权重分析

由表3可以发现6个素养不同水平的考查情况．

在数学抽象、逻辑推理、数学运算和数学建模4个素养中，各水平均是从较低水平到较高水平权重呈现递减分布，体现了3个水平之间的关系．按照知识学习水平的划分——知识理解、知识迁移和知识创新3个水平都是较高水平建立在较低水平之上．知识理解水平是基本水平和基础性知识学习要求，因此水平一所占比重最大；知识迁移水平是在知识理解之上的一个更高的要求水平，所占比重次之；而知识创新水平是建立在前两个水平之上，在“四基”基础上对学生探究性学习能力和综合运用知识能力的体现，也是对“四能”的综合体现，大多在压轴题出现，因此水平三所占权重最低．

与以上4个素养情况不同，直观想象水平一权重为3.87%，较大低于水平二权重9.78%，也低于水平三权重4.11%．这是因为与直观想象相关的题目，大多不是简单的理解基本图形的性质就能解决问题，而是多种知识的综合，需要把与图形相关的知识迁移到新情境中探索数学问题，考查综合能力，因此水平一低于水平二和水平三．直观想象的水平三权重相对于其它5个素养的水平三权重较大，主要是因为在立体几何、平面解析几何和函数题目等大题中，多数需要用到数形结合的思想，具有综合性，往往难度较大，需要自主探究和创新性地寻找解决问题的方法．

数据分析水平一、水平二权重分别为3.33%和4.67%，水平一低于水平二，与上述直观想象水平呈现的情况类似，考查数据分析的题目多数有现实背景，需要把已学的数据分析知识和方法迁移到新情境中，需达到水平二．两份学考和2018年文科高考关于数据分析素养考查的权重比其它卷的高，但重点都是对水平一、二的考查，这从一个角度体现数据分析水平一、二对普通人的重要性，从相关题目也可看出，其背景是常见的情景，涉及普通人需要处理的基本问题．

表3 各试卷数学核心素养水平指标权重汇总

3.3 高考与学考权重比较

高考和学考的考查目的不同．高考是为高校选拔人才提供主要依据，学考是以检测各地学生整体知识水平为目的，是学生高中毕业应达到的水平，因此二者对核心素养及其水平的考查情况存在差异．

图1为高考和学考6个数学核心素养考查权重柱状图．由图1知，高考和学考对6个数学核心素养的考查权重分布基本一致．这体现两种不同的考试均重视对6个数学核心素养的考查，且各数学核心素养在两种测试中的地位是相同的，在题目中的呈现方式也类似．

图1 高考与学考不同素养的平均权重

高考涉及的数学运算、逻辑推理、直观想象权重都相对更高．这是由于高考试题难度较大，同样知识内容的考查程度较深、综合性较强，常需要通过大量的计算和较为复杂的推理来解决问题，且涉及直观想象的题相对较多．

图2、图3、图4分别为高考与学考数学核心素养各水平的总体比较及年度比较．由图2知，高考和学考对3个水平的考查权重有较大差异．总体看，高考对6个数学核心素养3个水平的考查平均权重比例近似为37∶44∶19，而学考对3个水平的考查权重比例近似为61∶37∶2．这体现高考和学考的考查要求不同，高考要求学生在知识理解和知识迁移的基础上，还能够综合所学知识、方法、技能和数学思想，一定程度的自主探究和发现解决问题的思路和方法，即达到知识创新水平．学考则更强调基础性，主要要求学生的数学核心素养达到前两个水平，且更注重对水平一知识理解的要求，体现面向全体学生这一宗旨．

图2 高考与学考不同水平的平均权重

图3 2012年高考和学考不同水平对比

图4 2018年高考和学考不同水平对比

2017版课程标准对数学核心素养也进行了3级划分，其中的水平一（简称学业水平）是学业水平考试的要求，水平二（简称高考水平）是高考要求．从以上对比可看出，除2012年学考略涉及水平三，总体而言，学业水平正好对应喻平水平划分中的水平一、水平二；高考水平对应喻平水平划分中的水平一、二、三．因此喻平水平划分同样可体现学考和高考对数学核心素养的不同要求．

3.4 不同年份数学核心素养权重比较

图5显示，2012年和2018年各3份测评试卷对各素养考查年度平均权重分布无明显差异．虽然数学核心素养近几年才提出，2017版课程标准正式确定，但数学核心素养与数学思想方法和能力紧密相连，并蕴含在解决数学问题的过程中，其通过考题呈现的方式一直都相同，而学考和高考都是较为成熟的考试，因此，2012年的考卷与2018年间隔5年的考卷对数学核心素养的考查总体变化不大，与2017版课程标准的要求总体是一致的．

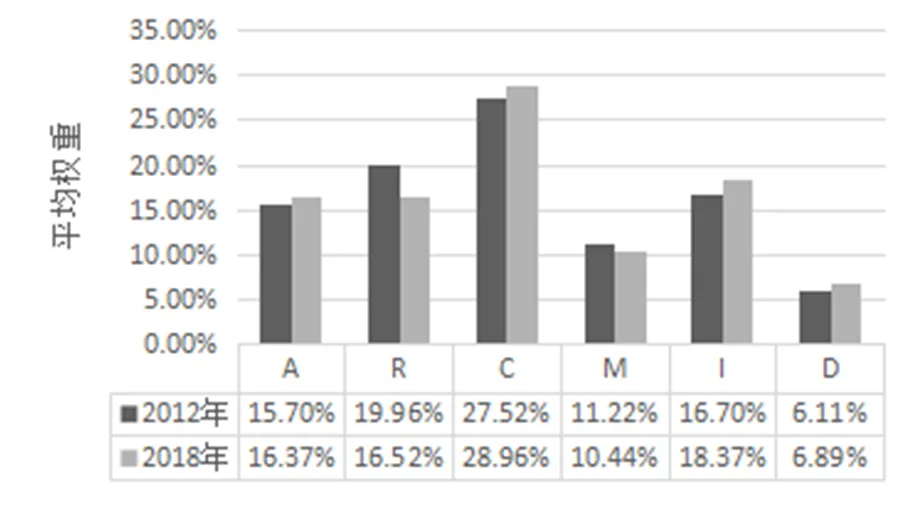
图5 2012年和2018年各素养比较

3.5 理科与文科数学核心素养权重比较

图6显示，理科和文科试卷各素养的考查权重分布基本一致．每年文、理科试卷都是大部分题目相同，略不同的常常是同一道题目背景下给出不同小题的情况，理科的问题相对于文科问题复杂，因此，图7显示理科卷对水平二和水平三的要求更高，文科更重视水平一的考查，这与文、理科不同的考查要求是吻合的．

图6 理科与文科不同素养权重比较

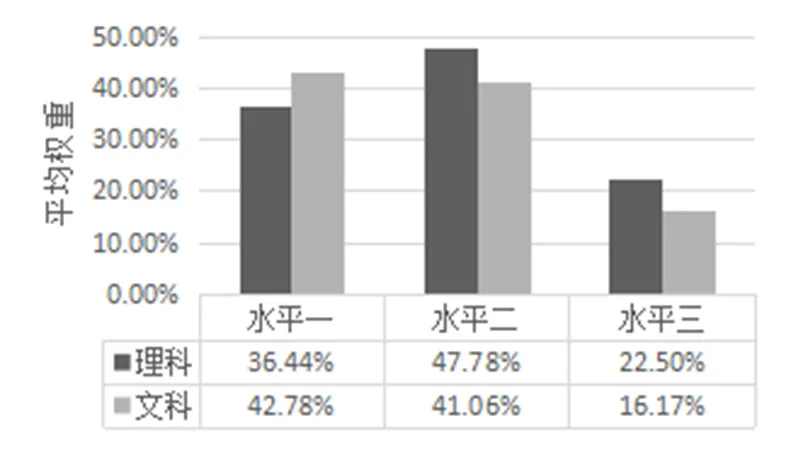
图7 文科与理科各水平权重比较

4 讨论

数学核心素养与数学思想方法和能力有机联系，蕴含在解决数学问题的全过程，有效解决每一道数学题，都需要达到相应的数学核心素养水平．无论提不提出数学核心素养概念，对其要求都实实在在蕴含在解题的过程中，2012年的考卷与2018年的考卷对数学核心素养的考查情况总体变化不大充分体现了这一点．解某一道题达到某一素养水平，并不能完全体现学生达到相应水平，需要通过整份试卷，多个题才能体现学生的实际水平．

2017版课程标准指出6个数学核心素养既相对独立，又相互交融，是一个有机整体．总体而言，它们在试卷中呈现的权重从大到小依次为，数学运算（28.35%）、逻辑推理（18.24%）、直观想象（17.76%）、数学抽象（16.04%）、数学建模（10.83%）、数据分析（8.78%），与它们之间的内在关系和在整体中的地位是一致的．前3个数学核心素养的权重体现了它们在数学核心素养中的基础性和解决问题中应用的广泛性．而数学抽象、数学建模往往是建立在这3个素养之上，没有这3个素养基础，就不可能有效提升数学抽象、数学建模素养，而在培养数学抽象、数学建模素养的活动中，3个基础素养也能得到更好提升．中国数学教育传统的双基训练和变式教学正是强化这3个基本核心素养的培养，这些好的传统需要在新的认识下发扬和完善．数据分析既有自己的独特性，又与除直观想象外的其它素养紧密相连．教学中要根据教学内容将6个数学核心素养有机联系，融会贯通，切不可孤立考虑各素养的培养．

应用数学的意识，特别是分析数据的意识对现代人越来越显重要，是所有学生应当具备的，数学建模和数据分析素养的培养应当进一步引起重视．从权重看，学考和高考对这两个素养的考查总体还略显不足，如何通过学考和高考，以及其它一些形式测评学生这两个素养水平需要进一步的探究，这两个素养的培养和测评需要有更多的、联系现实世界的数学实践活动，国内数学教育这方面还需加强．

学考对数学核心素养3个水平的考查情况充分体现：面向全体学生，教学中需要强调基础性，要强化各数学核心素养前两个水平的培养．在此基础上也才能有第三水平的提升．无论从国际视野或仅从国内来看，一方面，数学基础对全体公民的重要性都得到公认，另一方面，很多学生都惧怕数学，这样的现实背景下，中学数学教学需要处理好面向全体学生（重点要求数学核心素养前两个水平）与面向不同学生及学生的不同未来发展需求（分层要求第三个水平）的关系，应当加强这方面的研究．

5 研究结论

归纳梳理以上对6份试卷数学核心素养的分析，有如下结论．

总体而言，在6份试卷中，数学运算平均权重最大，数据分析平均权重最小，数学建模平均权重也较小，其余3个素养平均权重相近．

在数学抽象、逻辑推理、数学运算和数学建模4个素养中，3个水平均是从较低水平到较高水平权重呈现递减分布．而直观想象水平一权重明显低于水平二权重，也略低于水平三权重，其水平三权重相对于其它5个素养的水平三权重较大．数据分析水平一的权重也低于水平二．

两份学考和2018年文科高考关于数据分析素养考查的权重比其它卷的高，但重点都是对水平一、二的考查．

高考和学考对6个数学核心素养的考查权重分布总体基本一致，但对3个水平的考查权重差异较大，学考更强调基础性，要求学生数学核心素养达到前两个水平，且更注重对水平一知识理解的要求，体现面向全体学生这一宗旨．

2012年和2018年各3份测评试卷对各素养考查年度平均权重分布无明显差异，间隔5年的考卷对数学核心素养的考查总体变化不大．

理科和文科试卷各素养的考查权重分布基本一致，但理科对水平二、三的要求更高，文科更重视水平一的考查．

6 结语

喻平建立的数学核心素养评价指标框架有较好的理论基础和依据，但在具体操作中，依据指标体系对试题涉及的素养水平的标定有一定弹性，不容易精准标定．该研究虽然请中学有教学经验的教师共同研究确定各题的素养及水平标定，但仍然不够精准，导致获得的结论不够准确．建议课程标准编写组组织专家进一步制定操作性强，更加标准的数学核心素养评价指标体系，高考命题组组织专家对相当数量的试题进行数学核心素养水平的标定，在此基础上形成数学试题数学核心素养水平标定软件，更加精准有效评价高考试卷的数学核心素养考查情况，使每次的高考试卷对数学核心素养的考查更加稳定，这对今后一年两考的改革更显重要．有了较为标准的试题和试卷数学核心素养水平标定后，就可根据学生实际情况，测评学生实际数学核心素养水平，为教师的教学提供依据．

“美国不仅注重终结性评估的导向作用，而且注重形成性评估的反馈功能”[2]值得借鉴，通过试卷对学生数学核心素养的测评是终结性测评，对数学情感态度和价值观等隐性素养的测评还需要形成性的测评，这方面需要教育研究者和一线教师共同努力在理论和实践层面进行深入探索．

[1] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2018：4，80-89，100-106．

[2] 徐斌艳，蔡金法．关于数学素养测评及其践行[J]．全球教育展望，2017，46（9）：13-24．

[3] 胡典顺，雷沛瑶，刘婷．数学核心素养的测评：基于PISA测评框架与试题设计的视角[J]．教育测量与评价，2018（10）：40-46．

[4] 喻平．数学核心素养评价的一个框架[J]．数学教育学报，2017，26（2）：19-23．

[5] 喻平．基于核心素养的高中数学课程目标与学业评价[J]．课程·教材·教法，2018，38（1）：80-85．

[6] 朱先东，吴增生．核心素养视角下对数学测评的研究——以2017年浙江省中考试题为例[J]．数学教育学报，2017，26（5）：36-43．

[7] 张惠英，王瑞霖．基于核心素养的数学测评研究——以河北省2017年中考数学试题为例[J]．数学教育学报，2017，26（5）：31-35．

[8] 何萍，章才岔．基于核心素养视角的数学测评研究——以温州市2017年中考数学试题为例[J]．数学教学通讯，2018（10）：3-5．

[9] 张斌，苟斌娥．基于核心概念的数学测评解析与教学建议——以重庆市2018年中考数学试题（A卷）为例[J]．数学教育学报，2019，28（4）：61-65．

[10] 李作滨．素养导向的数学测评研究——以2018年高考为例[J]．数学教育学报，2018，27（6）：33-37．

[11] 李作滨．2018年13套高考数学试卷审思：基于核心素养的视角[J]．教育测量与评价，2019（4）：51-57，64．

[12] 彭艳贵，徐伟．高中生数学核心素养测评框架的理论分析[J]．教育理论与实践，2019，39（23）：49-52．

[13] 徐柱柱，张迪，綦春霞．初中生数学学科素养测评的实证研究——以北京市T区八年级为例[J]．教育测量与评价，2019（1）：53-58，61．

[14] 任子朝，陈昂，赵轩．数学核心素养评价研究[J]．课程·教材·教法，2018，38（5）：116-121．

Research on Mathematics Papers of Yunnan Senior High School Academic Level Examination and Its College Entrance Examination from the Perspective of Mathematics Core Competency

LI Shuang1, 2, YANG Ze-heng1, WANG Peng-de1

(1. Department of Mathematics and Computer, Dali University, Yunnan Dali 671003, China;2. Zhengzhou Fengyang Foreign Language School, Henan Zhengzhou 450000, China)

Under the framework of Yuping Mathematics Core Competency Evaluation Framework and Index System, the evaluation index system of high school Mathematics Core Competency was established. In addition, in this paper, mathematics test papers of the National College Entrance Examination Volume III for Arts and Science and the first half of Yunnan High School Academic Level Examination in 2012 and 2018, that is, a total of six papers were marked with mathematical core competency indicators, respectively. Through comparing and analyzing the distribution of each core competency and levels, the authors draws the following conclusions. The examination papers in 2012 and 2018 had little overall change in examining students’ mathematics core competencies. The distribution of weights of the six-core mathematic competency in the papers of National College Entrance Examination (including for Science and Liberal Arts) and Yunnan Senior High School Academic Level Examination of Mathematics was basically the same. The weight of the six-core mathematic competency in the examination papers, ranging from big to small, was mathematical operation, logical reasoning, visual imagination, mathematical abstraction, mathematical modeling, and data analysis, indicating that their internal inter-relations are consistent with their positions in the whole part. However, there were great differences in the weights of the three levels between the above-mentioned two kinds of examination. The reasons for these conclusions were also analyzed in this paper.

mathematics core competency; core competency assessment; mathematics test paper for College Entrance Examination; mathematics test paper for Academic Level

2020-08-07

国家自然科学地区基金项目——基于BISQ方程的高阶NAD方法数值模拟研究（41664005）；云南省教育厅教学改革项目——数学与应用数学专业学生实践能力培养体系建设的实践与研究（2013云南高校教改43）

李爽（1993—），女，河南郑州人，主要从事中学数学教学研究．杨泽恒为本文通讯作者．

G632.479

A

1004-9894（2020）06-0025-07

李爽，杨泽恒，王彭德．核心素养视角下云南高中学业水平考试和高考数学试卷分析[J]．数学教育学报，2020，29（6）：25-31．

[责任编校：张楠、陈汉君]