改进软位势的齐次玻尔兹曼方程柯西问题解的适定性

李浩光,文柯柯

(中南民族大学 数学与统计学学院, 武汉 430074)

1 相关知识

考虑如下齐次玻尔兹曼方程的柯西问题：

(1)

其中f=f(t,v)取决于时间t≥0，速度变量v∈R3.

玻尔兹曼方程是描述时间和空间演化的最成功的数学模型，从统计物理学的角度看就是描述稀薄气体中粒子的位置和速度的分布函数，一般通过相关的偏微分方程来描述这个运动.由于其深厚的物理背景，可测初值的玻尔兹曼方程解的存在唯一性、光滑性以及大时间渐近形态一直是许多数学家着迷的课题.麦克斯韦模型下齐次玻尔兹曼方程的研究已经取得了比较完善的结论[1-3]. 类似的动力学方程柯西问题解的适定性的相关研究可参阅文献[4].对于非麦克斯韦模型的齐次玻尔兹曼方程，受限于其复杂的结构，在很多时候没有获得满意的结论.MORIMOTO等在文献[3]中利用近似解的方法研究软位势玻尔兹曼解的存在性以及光滑性，没有稳定性的结论.

本文将探讨带可测初值的改进软位势齐次玻尔兹曼方程解的存在唯一性及稳定性.该方程的右边是一个二元碰撞算子：

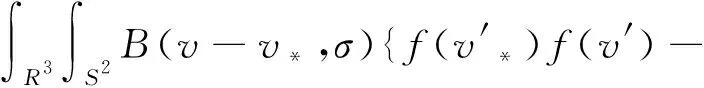
f(v*)f(v)}dσdv*,

对于-3<γ<0,考虑碰撞核函数Φ(z)=|z|γ傅里叶变换：

φt=G(φ),

这里：

|η|-3-γ)φ(η)φ(ξ-η)dηdσ,κ=ξ/|ξ|.

考虑到相函数|ξ|-3-γ在原点有奇异性，为此对位势函数做一点修改：

2 主要结果

(2)

(3)

关于Sobolev空间Kα，可以参考文献[3].

为证明定理1，先要证明以下定理2.

证明考虑空间Kα的定义，只需要证明对某个常数λ0>0，有：

(4)

这里记〈η〉=(1+|η|2)1/2.证明过程分为两部分：

(1)当|ξ|≤1时，考虑到对称性有：

〈-η+ξ-〉-6-γ-〈-η〉-6-γ|·

由微分中值定理(二阶)：

〈-η+ξ-〉-6-γ-〈-η〉-6-γ+(6+γ)η·

ξ-〈-η〉-8-γ=

〈-η+τξ-〉-10-γdτ,

从而得到：

|〈-η+ξ-〉-6-γ-〈-η〉-6-γ+

(6+γ)η·ξ-〈-η〉-8-γ|≤

同理可以证明：

|〈-η+ξ+〉-6-γ-〈-η+ξ〉-6-γ-

(6+γ)(η-ξ)·ξ-〈-η+ξ〉-8-γ|≤

又由于：

|η·ξ-〈-η〉-8-γ-(η-ξ)·ξ-〈-η+ξ〉-8-γ|≤

考虑到|ξ-|=|ξ|sinθ，得到：

|〈-η+ξ-ξ-〉-6-γ+〈-η+ξ-〉-6-γ-

〈-η+ξ〉-6-γ-〈-η〉-6-γ|≤

τξ-〉-8-γ+〈-η+τξ〉-8-γdτ,

由于|ξ|≤1,-2<γ<0,0<α≤1,则可求得：

〈-η+τξ-〉-8-γ](|η|α+|ξ-η|α)dτdη≤

考虑到：

于是有结论：

其中λ0依赖于γ,α.

当|ξ|>1时，直接计算可得：

做适当平移变换和球坐标变换，且考虑到：

-2<γ<0,0<α≤1,

可以得到：

于是：

综上所述，可以找到一个正常数距离λ0满足公式(4)，命题得证.

定义算子：

由方程：

可得：

从而：

由定理1可得：

当T0>0足够小时，使得λ0T0<1时，H是一个压缩映射.

由Banach不动点定理可得，上述问题存在一个唯一解φ(ξ,t)∈C([0,T0],Kα).即，带可测初值的改进软位势齐次玻尔兹曼方程存在唯一解.以φ(ξ,T0)∈Kα作为初值代回柯西问题(2)中，利用定理2，可得到带可测初值的改进软位势齐次玻尔兹曼方程存在唯一解φ(ξ,t)∈C([T0,2T0],Kα).重复上述过程可以得到φ(ξ,t)∈C([0,∞),Kα).

利用定理2，可得：

λ0‖φ-φ‖α.

计算上述微分方程得到：

这就证得公式(3)，定理1证毕.