基于改进蚁群算法的QoS路由研究
尹凤杰,褚群森
(辽宁大学 信息学院,辽宁 沈阳 110036)
0 引言
近年来,网络技术快速发展,多媒体数据的传输已经占据更重要的地位,这些业务对网络的服务质量[1](Quality of Service,QoS)要求不断增强.多约束QoS问题在文献[2]中已经被证实是一个NP-Complete难题.目前,研究发现各类智能算法的优势突出,国内外学者针对网络路由并结合智能算法的特性进行了深入的研究,提出了多种算法.文献[3]提出一种基于蛙跳算法的自适应多径路由算法以解决无线传感器网络中的拥堵难题.文献[4]提出基于遗传算法(Grenetic Algorithm,GA)的路由算法,该算法针对多约束离散网络节点的路由寻址问题,得到较为实用的解,但是正反馈能力不足是明显缺点.文献[5]提出了一种基于分数布谷鸟搜索的移动自组网QoS感知路由的多路径选择方案,通过考虑诸如能量、链路寿命、距离和延迟之类的QoS约束,开发了一种新的适应度函数,但可行性不高.文献[6-10]基于蚁群算法对多约束QoS路由算法进行不同的优化,优化后的算法性能从不同角度得到提升,然而,这些算法在一定程度上存在局限性,如搜索前期信息素含量较为匮乏,容易出现盲目搜索、局部最优等现象.
针对上述问题,本文设计一种基于传统蚁群算法的改进算法,使改进后的算法在保持较强的正反馈性和较高的收敛性的前提下,同时具备随机搜索的特征,扩大搜索范围,以保证最终解空间的丰富性.
1 多约束QoS路由数学模型
多约束QoS路由是指从源节点开始,建立一条到达目的节点的路由路径,与此同时该路径满足全部路由约束条件.因此可采用参考文献[11]中的网络模型.
采用与文献[11]相同的无向图G=(V,E)表示多约束QoS路由的网络模型,其中V表示网络中的全部路由节点,E表示网络中全部可通信的链路,r为节点的可交互范围,d表示节点间的距离,若d≤r,则两个节点之间存在一条可通信的链路e,且e∈E.给定的无向图G=(V,E),源节点到目的节点的路径集合为P,对于一条路径p∈P的边集为E(p),节点集为N(p),则QoS的参数定义如下:
(1)
2)带宽:BandWidth(p)=min{BandWidth(e),e∈E(p)}
(2)
(3)
(4)
式(1)~(4)分别将网络中最重要的4个制约因素用数学公式的形式表达出来,QoS路由算法的目地即为寻找一条满足如下条件的路由路径p′.
时延约束:Delay(p′)≤Dmax;
带宽约束:BandWidth(p′)≥Bmin;
丢包率约束:Lost(p′)≤Lmax;
开销约束:Cost(p′)最小(式(1)~(3)全满足).
2 蚁群算法改进策略
蚁群算法运行初期由于路径上的初始信息素分布较少,不具有明显的引导作用,此时算法的搜索速度较低;随着算法搜索的不断深入,路径上的信息素浓度不断加强,此时蚁群算法的正反馈特性突显作用,则容易导致蚁群算法在后续的迭代进程中对某一条路径的搜索持续进行,从而忽视对周围路径的搜索,导致无法输出最优的路径.
综合考虑上述问题,本文在蚁群算法[12](Ant Colony System,ACS)的基础上,设计动态自适应的转移概率因子,同时,对全局信息素更新规则进行了优化,以此来克服ACS算法的一些不足.
2.1 转移概率因子的设计
在ACS算法中,状态转移因子取值不同,蚂蚁按照不同的方式筛选下一跳节点,丰富了下一跳节点的可选择性,在一定程度上可以有效地防止算法陷入局部最优解.在公式(5)中状态转移因子q0是区间[0,1]内的一个常数,缺乏自适应性.
(5)
(6)
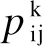
根据分析,当q0的值越大,下一跳节点越倾向于选择集合[τij]α[ηij]β中的值最大的节点,因此算法的收敛速度越高,算法的随机搜索能力越低;当q0的值越小,下一跳节点的选择越倾向于按照概率进行路径搜索,此时,算法的随机搜索能力增强,同时算法的整体收敛速度下降[13].
因此,本文设计转移概率因子函数q0(t),在算法执行的初始阶段,令q0的取值保持在较大的范围内,此时下一跳节点按照先验规律进行选择,算法具有高收敛性和低随机性;算法进一步执行,若继续保持算法初期的高收敛性,则容易导致算法陷入局部最优解而无法摆脱,此时需选择较小q0,算法具有较高的随机搜索性和较低的收敛性;算法继续执行,输出结果趋于稳定,算法的高随机性已经不能继续丰富最优路径的集合,重新恢复较大的q0,进一步提高收敛速度并最终找到全局最优解.
综上所述,自适应函数q0(t)满足在算法执行的各个阶段对收敛速度和随机搜索能力的要求.q0按下式进行选择:
(7)
式中:t为迭代次数;qmin为q0(t)的最小值;σ为正参数,控制q0(t)上升和下降的速度.
2.2 全局信息素更新规则的改进
在ACS算法中,每次迭代完成后只有当前全局最优蚂蚁经过的路径上的信息素浓度得到加强,全局信息素更新规则如下:
τij=(1-ρ)τij+ρΔτij
(8)
(9)
式中:Δτij为路径(i,j)上的信息素的增长强度;ρ为信息素挥发因子;Q为每代蚂蚁携带的可释放信息素总量;PBest为当前全局最优路径的长度.ACS算法信息素更新规则仅增强了当前全局最优路径上的信息素浓度;同时,由于信息素的挥发行为,其他的路径上信息素浓度下降.综合考虑,这种更新规则突显了当前最优路径上的信息素对后续蚂蚁的吸引效果,对进一步迭代的搜索过程具有指导作用.
ACS算法的信息素更新规则选择比当代最优路径更好的全局最优路径进行释放信息素,这一过程完全忽视了当代最优路径对构建最终解空间的作用.文献[14]通过实验进行验证,仅更新全局最优路径上的信息素浓度与更新当代最优路径上信息素浓度进行对比,实验结果表明前者的引导作用要优于后者.无论是对全局最优路径还是对当代最优路径上信息素的增强,对最终解空间的构造都具有重要的指导性,使得下一次迭代过程对此次信息素所更新的路径以及该路径的邻近路径进行进一步搜索.因此,增加了得到最终全局最优路径的概率,与此同时,收敛速度也得到提高.正如文献[14]所说,此时全局最优的性能并没有比当代最优的性能更加优越,仅稍强于后者,若将二者同时利用起来有可能使改进后的算法具有更加优越的性能.
本文在ACS算法全局信息素更新规则的基础上,设计一种新的更新规则.结合最大最小蚁群算法[15]对各路径上的信息素含量进行限制,即网络中任意一条的路径的信息素含量限制在[τmin,τmax]范围内,当超出这个范围时,信息素含量强制限定为τmin或τmax,下确界可以防止某条路径信息素含量过低进入停滞搜索状态,而上确界可以避免某条路径信息素含量过高,算法陷入局部最优解.
为了加快算法的收敛效率,综合考量全局最优路径和当代最优路径的影响,本文采用对全局最优路径以及当代最优路径同时进行信息素的更新.当代最优路径(k,l)与全局最优路径(i,j)为同一路径时,此时该路径上的信息素增量大于仅对全局最优路径进行更新的信息素增量,提高了算法的收敛速度.当代最优路径(k,l)与全局最优路径(i,j)为两条路径时,同时对两条路径上的信息素进行增强,扩大了最优解的搜索范围,增加了对次最优解的搜索深度,降低算法陷入局部最优解的概率.
此时信息素增量Δτij(t)的计算公式如下:
(10)
式中:PBest′表示此次迭代过程产生的最优路径;PBest表示迭代至今产生的整体最优路径.
3 改进蚁群算法在多约束QoS路由中的应用
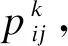
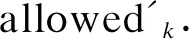
(11)
(12)
(13)
此时,开销函数Cost(p)可以用公式(14)来表示:
(14)
式中:ω1、ω2、ω3分别为时延、带宽和丢包率所占权重,同时,ω1+ω2+ω3=1且ω1、ω2、ω3≥0.在基于蚁群算法的QoS路由算法中,路径启发式信息ηij相应的表达式如下:
(15)
基于改进蚁群算法QoS路由路径搜索步骤:
1)初始化网络参数.
2)源节点s收到发送数据请求,按照改进后的蚁群算法发出M个“蚂蚁帧”,每个“蚂蚁帧”生成各自的路由表,将源节点s和目的节点d加入到路由表,并随机生成一个q.
3)“蚂蚁帧”根据概率转移因子q0与q的关系,来选择下一跳节点的寻找方式,当“蚂蚁帧”到达下一跳节点时,则将当前节点记录到“蚂蚁帧”中.
4)对当前蚂蚁帧所处节点进行判断,若此时蚂蚁帧位于目标节点d,则更新路由表中的相关记录,并计算相应开销函数;否则按照步骤3)继续进行路径搜索,直到找到目标节点或者完成TTL时间,此时当代蚂蚁帧完成搜索.
5)比较M个蚂蚁帧所记录的开销函数的大小,找到当代最优路径;比较当代最优路径的开销函数与上一次迭代后的全局最优路径的开销函数,找到本次迭代完成后的两类最优路径,按照改进后的信息素更新规则,对这两条路径上的信息素浓度进行加强,并更新路由表中相应的数据.
6)下次迭代开始前自适应改变算法中相关参数的值,接着将迭代次数增加1.
7)重复执行算法的第3)~6)步直至“蚂蚁帧”生命周期结束或算法运行周期结束,并向源节点返回路由路径信息.
4 仿真实验及分析
本文利用Matlab进行仿真实验,模拟在1 000 km×1 000 km范围内随机生成35个网络节点,节点之间随机连通,构建可通信的链路,同时生成相应的网络参数,如链路时延、节点时延、带宽、丢包率、开销等.网络拓扑图如图 1 所示.
仿真实验网络相关的参数选择如表 1 所示.
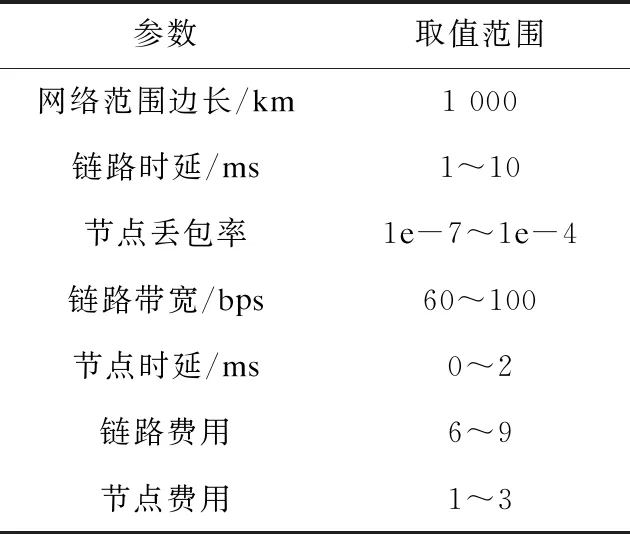
表1 网络相关参数
在仿真实验中,有关参数的设置如下:
QoS约束条件参数:Bmin=60,Dmax=100 ms,Lmax=1e-2.
算法中各参数的设置:α=2,β=2,Q=10,M=20,k=10,ρ=0.1,源节点s=1,目的节点d=35,最大迭代次数N=100.
仿真实验表明最优路径为(1,3,9,17,23,28,35),实验归一化开销为3.21.
仿真图像2表明,在初期搜索阶段,两种算法均未找到较好的路径,此时延迟比较大,根据归一化延迟计算公式,此时归一化延迟趋于0;当路径搜索平稳时,改进蚁群算法的归一化延迟高于基本蚁群算法,说明改进蚁群算法得到的路径延迟优于基本蚁群算法路径的延迟.图像3表明随着迭代进程的不断进行,改进蚁群算法费用曲线的下降速度明显高于基本蚁群算法,改进蚁群算法最终搜索到的路径的费用明显低于基本蚁群算法,表明基本蚁群算法在搜索过程中搜索深度不足,陷入局部最优解,而改进后的算法通过限制信息素的持续增长,避免了这种情况,得到更加优秀的路径.改进蚁群算法在迭代次数22左右趋于稳定,而基本蚁群算法则在迭代次数39左右趋于稳定,实验结果表明在收敛特性上,改进蚁群算法比基本蚁群算法更优秀.
这是由于改进蚁群算法在迭代搜索初期阶段通过设置了较大的概率转移因子q0,降低算法的随机性,有利于初期路径上信息素的积累;在算法中期,选择较小的q0,此时改进算法与基本蚁群算法保持一致的全局搜索性,同时通过最大最小蚁群策略限制了信息素在某一路径的大量积累;同时依照优化后的信息素更新规则对信息素进行更新,对当代最优路径和全局最优路径进行信息素更新,进一步强化算法的收敛性,使算法不断朝着全局最优目标进一步寻找.
5 结束语
蚁群算法由于算法自身具有较强的正反馈作用,针对多约束条件下的网络路由路径寻优问题经实验验证有较好的效果.本文设计了随时间变化的转移概率因子函数q0(t),较好地控制了下一跳节点在不同时期的搜索范围;同时,设计了一种新的信息素更新的规则,在一定程度上加强了算法的整体收敛速度.这种改进算法与多约束QoS路由模型结合起来,构造了基于改进蚁群算法的路由算法.实验仿真结果表明,改进的路由算法的路径搜索速度得到提高,路由路径传输数据的开销较低,得到了比较理想的实验结果.

