考虑效率与公平的城轨网络客流协同控制优化模型

郇 宁 张金萌 姚恩建

(1北京交通大学综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044)(2交通运输部规划研究院，北京 100028)

随着城市轨道交通线网的不断扩展，客流需求呈持续增长态势，高峰期客流需求与运输能力的矛盾日益凸显，大客流车站乘客的出行延误持续增加，站台拥挤日益加剧.传统的客流控制方法依靠站务人员的经验，对站内滞留乘客较多、拥挤较为严重的车站采取客流控制措施，未考虑车站间与线路间客流的交互作用，难以实现网络运力资源的协同高效利用，易造成部分站台乘客超长滞留的现象，不利于提升通勤出行满意度与吸引力.

针对城市轨道交通的客流控制问题，国内外学者已开展了大量研究工作.黄文慧等[1]从路网和客流的交互机理出发，建立了城市轨道交通线路客流拥挤传播模型，进而提出一种车站流入调整量计算方法；Jiang等[2]以车站最佳流率作为决策变量，采用强化学习方法解决了城轨客流控制问题；黄倩[3]以站台聚集人数和上车人数作为决策变量，建立了乘客输送量最大化、滞留总时间最小化的多目标优化模型.

考虑到单线客流控制模型在应用中局限性较大，部分学者研究了以局部路网为案例的多线影响下的客流控制模型.Xu等[4]基于客流演变和乘客路径选择行为提出了一种考虑进站与换乘客流的网络客流协同控制模型；Shi等[5]以乘客总等待时间最小化和车站间拥挤风险水平最小化为目标，提出了一种考虑运行风险阈值的客流协同控制方法；谢丽平[6]在客流控制问题中融入了网络客流分布的时变特性，以网络上车人数最大化和乘客总延误时间最小化为目标函数，建立了网络客流演化分布及点线能力约束；温念慈[7]以列车能力利用率最大化和乘客平均延误时间最小化为目标，构建了网络客流协同控制模型；姚向明等[8]以客流需求与输送能力匹配度最大化和延误客流量最小化为目标，计算车站分时最佳流入量.上述研究重点在于提升线网运输效率、降低乘客总体延误，对于城市轨道交通服务公平性的考虑仍有不足.

针对高峰期部分车站乘客进站延误过长、服务水平不均衡等问题，马羽等[9]以车站间乘客均衡候车为优化目标，构建了线路层面多站间客流协同控制模型；姜曼[10]以上车总人数最大化和各站上车比例方差最小化为目标，构建了单线多站客流协同控制模型.然而，这些研究仅关注进站与出站客流对车站拥挤状况的影响，未考虑线路间换乘客流对本线运行状态的冲击，故难以准确反映网络的整体运行状态.

鉴于此，本文立足于城市轨道交通的效率与公平服务特性，提出网络层面的客流协同控制多目标优化模型，以全网列车平均运能利用率最大化和乘客滞留比差异最小化为目标，建立列车运能、区间流量传播、站台到达与滞留等系列约束，求解最优客流控制方案，以期为客流控制工作提供科学的方法指导.

1 城轨客流控制组织形式

近年来，客流控制已成为我国各大城市轨道交通运营管理的常态化工作.以广州地铁为例，2019年12月实施客流控制方案，在全网运营的248个车站中，在早高峰7:00—9:30时段，对22个主控车站和23个辅控车站进行客流控制；在晚高峰17:30—20:30时段，对14个主控车站和2个辅控车站进行客流控制.在实施层面上，车站管理人员通过调整站内、外的客流组织模式，对所在车站的进站量和换乘量进行控制.

客流控制的主要手段可分为限速控制和限时控制，前者通过设置导流围栏减缓乘客进站、安检速度；后者在进站口或换乘通道处进行临时拦截[11]，以削弱短时内客流涌入对站台的冲击.高峰期车站客流组织形式见图1.

图1 高峰期车站客流组织形式示意图

车站客流状态不仅受本站客流的影响，还与上游车站的客流传播密切相关.若上游车站占据过多运能，易造成本站乘客大量滞留，引发下游系列拥堵.同时，在网络化运营条件下，线路间换乘客流的交互使得网络客流分布愈发复杂.因此，为实现有限运输资源的高效、公平利用，亟需提出一种能够适应网络客流传播特性的客流协同控制方法.

2 城轨网络客流协同控制优化模型

2.1 参数定义及假设

定义T为客流控制时段的集合，t∈T；Δt为每个单元时长；S为站台的集合，s∈S；L为线路的集合，l∈L，且S与L存在映射关系，即S→L；D为线路方向的集合，d∈D，其中d=1表示上行方向，d=2表示下行方向；K为车站类型的集合，k∈K，其中k=1表示非换乘站，k=2表示换乘站.

模型的基本假设如下：①不考虑列车延误等突发事件对实际列车运行计划的影响；②认为工作日通勤客流分布及换乘结构稳定，各线路、车站及方向的下车率及换入率由上一季度运营数据测算获得，根据序列相关性检验原理[12]，以60 min长度的时间窗进行赋值.

2.2 目标函数

为保证线网运输能力充分利用，以各控制时段内全网列车平均运能利用率最大化为优化目标，即

(1)

(2)

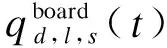
为避免过度追求运能利用效率而造成的乘客出行延误差异加剧，以各控制时段内全网各站台乘客滞留比差异最小化为另一优化目标，即

(3)

(4)

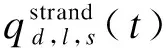
2.3 线路运输能力约束

线路运输能力受列车编组、车厢定员、发车间隔、乘客分布等因素影响.时段t内，线路l在方向d上的运输能力cd,l(t)可表示为

cd,l(t)=λMlnd,l(t)

(5)

(6)

2.4 区间流量传播约束

(7)

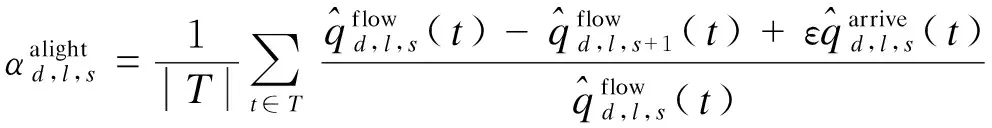
(8)

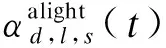
(9)

(10)

(11)

式中，γ为上车人数比例最低阈值，取值为0.4.

2.5 站台到达与滞留约束

站台到达客流由进站客流和连接线路换入客流2个部分组成，即

(12)

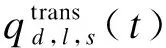
(13)

(14)

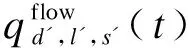
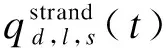
(15)

实施层面上，管理者可通过控制进站和换乘流率间接干预上车人数，从而达到预期的控制效果.同时，应确保站台的候车人数上限不能超过承载阈值，即

(16)

式中，ηs为站台s的安全承载人数.

2.6 其他约束

模型中的其他非负约束为

(17)

(18)

2.7 模型构建与求解

以各控制时段内各站台的上车人数为决策变量，建立以全网列车平均运能利用率最大化(式(2))和乘客滞留比差异最小化(式(4))为目标的优化模型.采用理想点法，令优化目标尽可能地接近各自的理想值，从而将多目标优化转换为单目标优化问题，即

(19)

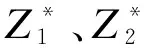
在由式(1)、(3)、(5)～(7)、(9)～(13)、(15)～(18)确定的可行域内，采用遗传算法对优化模型进行求解.每个时段内每个车站的上车人数构成一个基因位，全网所有车站在各个时段内的上车人数共同构成一条染色体.每条染色体的基因位数量固定，基因位的二进制编码由式(9)中决策变量的上下阈限及精度决定.通过设置轮盘赌选择、均匀交叉及随机多点变异过程，确保所求解的质量.当适应度曲线趋于收敛时，便可得到该可行域内的最优解.

3 实例验证

3.1 线网概况

选取广州地铁线网中广州火车站、海珠广场、东山口等23个车站所处的通勤大客流区域为研究对象，即|S|=20.图2为局部网络的拓扑结构.该局部网络内线路的运输能力见表1.

3.2 最优客流控制方案

求解过程中，设置遗传算法种群规模为100，最大迭代次数为2 000，交叉概率为0.95，变异概率为0.05.表2为所求解的最优上车人数方案.其中，换乘车站的站台分别计入所属线路.

以断面满载率评估客流控制实施成效.图3给出了优化前的断面满载率分布.由图可知，7:00—8:00为早高峰形成初期，客流尚未形成一定规模，运能相对充沛，网络断面满载率基本处于75%以内.8:00后，通勤客流大量涌入线网，5号线和1号线的部分断面满载率接近上限.

图4给出了优化后的断面满载率分布.由图可知，在运输效率和服务公平的双重约束下，高满载率断面的载荷显著降低.空间上，拥挤区域向相连区间和线路疏散；时间上，拥挤时段向峰前和峰后疏解，起到了削峰填谷的效果.说明优化所得的客流控制方案能够有效调节满载率的时空分布状态.

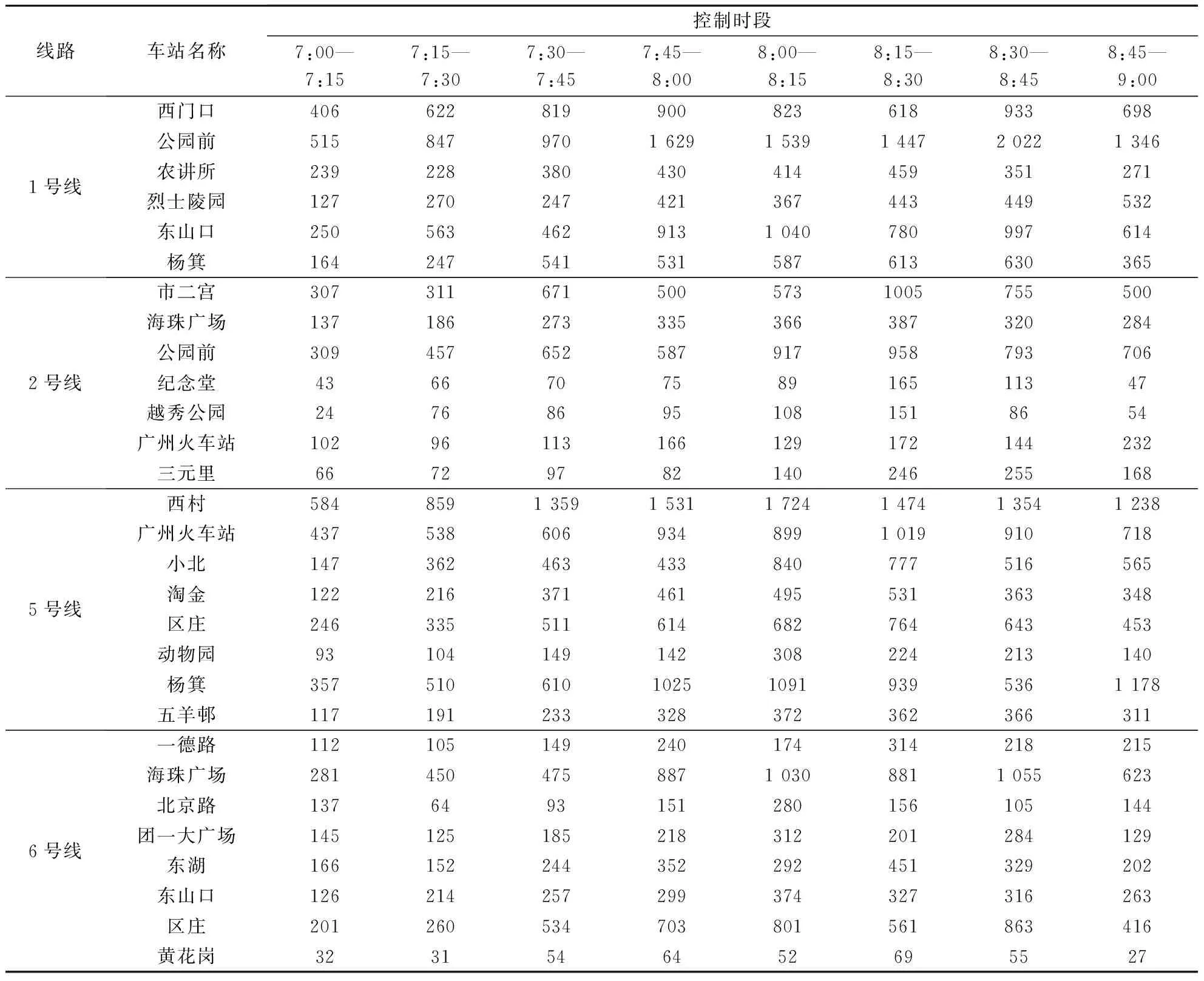
表2 控制时段内站台最优上车人数

(c) 5号线

(c) 5号线

基于优化前、后网络的断面满载率分布，进一步对比最高满载率断面的时空分布情况，以评估该模型在缓解瓶颈区间拥堵方面的作用，结果见表3.

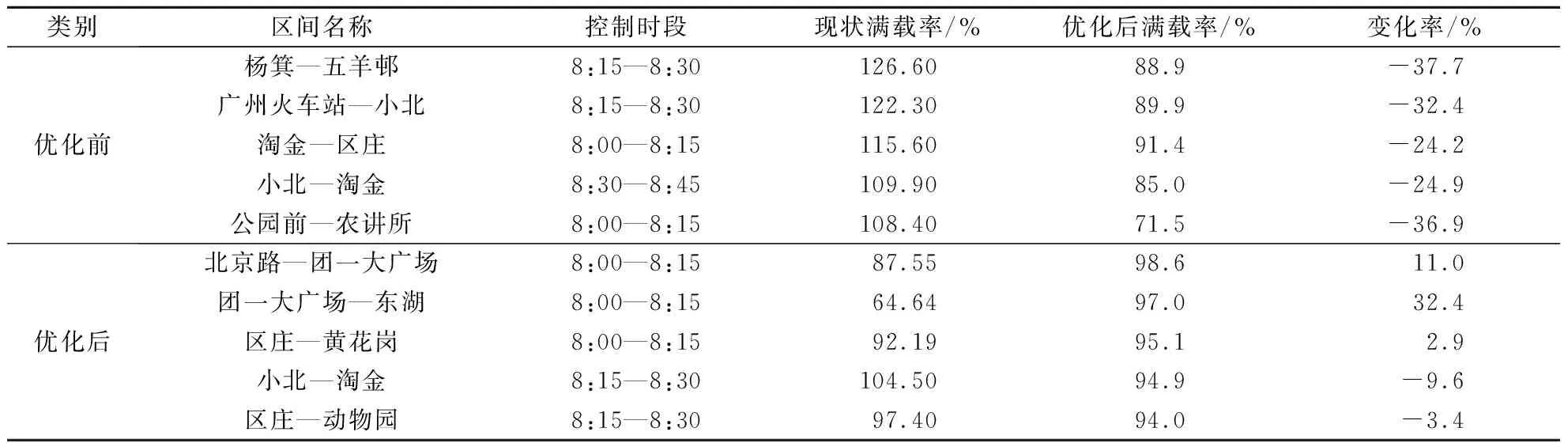
表3 优化前、后最高断面满载率区间对比

由表3可知，优化前杨箕—五羊邨区间满载率处于最高水平，引入最优控制方案后，该区段在相同时段内的满载率由126.6%降至37.7%，而北京路—团一大广场则成为满载率最高区间.在网络层面上，断面最高满载率由126.6%降至98.6%，最高负载时段由8:15—8:30前移至8:00—8:15，显著改善了瓶颈区间的拥堵状态.

利用Gini系数量化满载率分布的均衡性[14-15]，分别计算优化前、后的断面满载率Gini系数，结果见表4.根据国际Gini系数评价标准[15]，[0, 0.2)表示绝对平均，[0.2, 0.3)表示比较平均，[0.3, 0.4)表示相对合理.由表可知，在最优客流控制方案下，局部网络的断面满载率Gini系数由0.301降至0.292，说明所提模型有助于促进网络负载的均匀分布.

图5给出了站台层面候车乘客的滞留比分布情况.由图可知，滞留较高车站的邻近车站也存在滞留现象，表明运能分配较为合理.同一车站不存在连续时段高滞留比的现象，表明该模型可改善车站间滞留不均、部分乘客超长滞留的现象.换乘车站的滞留比波动较大，这与换乘客流分批到达相关.

表4 优化前、后断面满载率Gini系数对比

图5 站台候车乘客滞留比分布

为评估效率优先型策略(简称策略1)与兼顾效率与公平型策略(简称策略2)的差异性，探究公平性因素在解决城轨客流控制问题中的合理性.以式(2)作为策略1的目标函数，以式(2)、(4)作为策略2的目标函数，对比2种策略下的优化效果，结果见表5.由表可知，策略2的高峰期运能利用率为0.791 9,与策略1的0.791 5基本持平，且使乘客滞留比标准差由0.124 7降至0.105 2，仅在需求满足率上存在0.04%的小幅下降.由此可见，促进服务公平性与实现效率最大化间不存在显著冲突，且有助于改善高峰期的通勤服务水平，提升客流控制背景下的乘客出行满意度，适用性更优.

表5 不同优化策略效果对比

4 结论

1) 为解决城轨网络客流协同控制问题，以运输效率最大化和乘客滞留比差异最小化为目标，构建了体现客流传播特性且兼顾效率与公平的优化模型.达成最优的高峰期运能利用率为0.791 5，乘客滞留比标准差为0.105 2，缓解了部分站台乘客超长滞留的情况，彰显公共交通无差异的服务理念.

2) 基于广州地铁线网的实例中，所构建模型能够使最高断面满载率由126.6%降至98.6%，表明在缓解瓶颈区间高负载方面成效显著；断面满载率Gini系数由0.301降至0.292，表明该模型有助于实现高峰期网络负载均衡，降低运行风险.

3) 通过对比效率优先型策略和兼顾效率与公平型策略的优化效果，论证了公平性因素的引入有助于进一步提升网络运能利用率，二者不存在显著冲突，且有助于提高常态客流控制措施下的通勤服务水平和乘客出行满意度.