高性能计算支持的静气弹优化设计方法

黄 勇 孟德虹* 罗振先 孙 岩 王运涛 王晓军 孙俊峰

（1.中国空气动力研究与发展中心，绵阳 621000；2.北京航空航天大学，北京 100083）

0 引言

从2010 年以来，国内超级计算机的实测运算速度已跨越P级(PetaFlops，即每秒千万亿次浮点运算)门槛，正向E级(ExaFlops，即每秒百亿亿次浮点运算)进发。“天河一号A”达到了2.507 P、“星云”达到了1.27 P。“天河二号”的峰值运算速度为54.9 P，持续速度为33.9 P。2016 年，“神威·太湖之光” 的峰值运算速度达到了125.4 P(约0.125 E)，持续速度为93.0 P。因此，可以说我国已经进入基于超级计算机的高性能计算时代。

然而，就像美国怀俄明大学机械工程系教授Mavriplis等人[1]2007 年在美国看到的那样：“计算方法正在成为除理论和实验之外科学探索的第三支柱，基于这样的认识，科学界越来越推崇高性能计算。但另一方面，计算工程却持续地降格为一种在商品化计算机硬件上运行的成熟软件应用，以为工程问题不够复杂，不需要部署如此大规模的先进硬件。”Mavriplis等人[1]认为千万亿次计算机给航空基础研究带来了机遇，“工程应用能从高性能计算方法的进取计划中得到同样的好处，这些问题至少同科学问题一样重要，尤其是那些关系到国家竞争实力的问题”。计算航空科学领域的“耦合多学科的数值模拟和航空航天飞行器全任务包线内的设计优化”就是这类问题，因为单学科模拟的问题相对更为成熟。

作为计算航空科学的重要组成部分，CFD的发展和应用在过去五十年里极大地得益于计算机硬件的进步，下一步从RANS 计算向LES 方向发展，也需要计算机硬件更大的进步来支持。但是，美国斯坦福大学的Witherden 和Jameson[2]指出，目前高性能计算硬件的变化，给CFD数值算法设计带来了新的约束。如处理器运算能力和内存带宽的不平衡发展、大规模并行加速器(GPU和协处理器)带来的异构/异步问题、节点通讯的延时问题等等，使一种算法要适用于高效的大规模并行计算，也变得很不容易了。设计数值算法要从原来尽量减少浮点运算数量，转到考虑算法运算强度上去；对传输的每字节数据，都要考虑执行了多少有用的计算。也就是说，对一些早期开发的大型工程应用程序而言，要高效地使用目前的超级计算机，也是件困难的事。

国内情况更是如此：超级计算机在航空航天领域的应用还不够广泛深入，航空航天领域原先自研的大型应用程序，对最新超级计算机的计算潜力挖掘得还不够。为此，科技部国家重点研发计划“高性能计算”重点专项，在2016 年启动了“数值飞行器原型系统开发”项目，旨在提高航空航天领域自研应用软件适应国内超级计算机最新硬件的能力。考虑大规模设计变量的气动-结构综合优化方法开发是其中的一个子项，本文讨论这个领域的一个主要问题：考虑静气弹变形影响的高速大展弦比机翼设计方法。

国内有关文献可追溯到1999 年詹浩等人[3]的改进余量修正法工作，当时通过全速势方程和工程梁理论耦合计算机翼的弹性变形。2009 年詹浩等人[4]在余量修正反设计方法中，气动载荷及机翼结构弹性变形通过基于非结构网格的三维Euler方程耦合结构力学平衡方程求解。2012 年王晓江等人[5]再次用余量修正法发展基于静气动弹性的机翼型架外形设计方法，但采用三维NS 方程的有限体积法和结构有限元方法弱耦合计算变形。

对线性小变形，迭代/修正方法的“性价比”其实挺高。2002 年梁强等人[6]耦合三维NS 方程与机翼弹性平衡方程，计算几何扭转角分布，对其迭代更新进行机翼型架外形设计。2011 年杨国伟等人[7]基于混合网格的NS 方程和结构柔度矩阵方法的耦合求解变形，不进行迭代计算，直接采用结构负载的卸载方法，从巡航飞行外形反推地面型架外形所需要的结构变形量。2012 年林跃胜等人[8]对反向加载得到的初始型架外形，采用修正的偶极子格网法计算气动力，发展机翼型架外形的快速设计方法。2014 年黄江涛等人[9]也采用结构负载的卸载方法，但在型架外形逆推、修正及静气动弹性复核中，验证了其CFD网格变形和CFD/CSD数据交换技术的效率和精度。

在基于梯度优化设计方法中，国内目前有三类工作。只用气动梯度的，如2009 年熊俊涛等人[10]在机翼的控制论优化设计方法中，通过Euler方程和结构静平衡方程耦合，求解机翼在跨声速巡航飞行状态下达到结构弹性平衡时的弹性变形及真实气动载荷。气动梯度和结构梯度都用的，如2018 年徐兆可等人[11]用基于梯度的SQP算法进行机翼气动结构优化设计，其中气动力通过Euler方程与结构平衡方程的静气弹耦合计算得到；在此基础上，升阻力系数的梯度通过求解流场伴随方程获得，翼盒结构质量的梯度直接计算求得，应力梯度通过扰动结构设计变量采用有限差分方法获得。还有计划用气动和结构交叉梯度的，如2018 年黄江涛等人[12]的工作，为高效地计算优化目标相对气动和结构设计变量的梯度，针对RANS 和结构平衡方程的耦合系统，研究了其对应耦合伴随方程的延迟数值计算方法。

基于代理模型的优化设计方法，考虑计算资源限制，仅在样本分析中采用高保真耦合模型。2006年刘金辉等人[13]基于响应面的多目标多约束优化设计方法中，通过三维Euler方程的有限体积法和机翼弹性平衡方程的有限元方法的耦合迭代计算静气弹变形。2014 年左英桃等人[14]基于Kriging模型利用遗传算法优化设计，其中结构分析用有限元方法计算，气动载荷用RANS 方程计算，流固耦合界面数据插值采用RBF插值方法。2017 年聂雪媛等人[15]采用Kriging模型结合改进的粒子群优化方法，基于杨国伟的CFD/CSD耦合分析，对大飞机的结构刚度进行了优化设计研究。

不用代理模型的智能优化设计方法，考虑计算资源限制，需要快速的耦合计算，采用的模型保真度低些。2013 年杨佑绪等人[16]基于遗传算法提出一种气动弹性综合优化设计方法，采用等效板多板模型计算翼面结构动力学特性，利用面元法计算气动力，在考虑颤振速度、静气动弹性变形约束的情况下，以结构质量最小为目标开展了优化设计方法研究。2017 年杨体浩等人[17]使用改进的微分进化算法优化，在静气弹耦合计算上气动力用快速的全速势方程加附面层修正计算，而结构减重优化用商业软件实现。

回顾以上设计方法研究(不包括MDO方法和全商业软件集成的工作)可以看出，过去二十年里，静气弹耦合计算用的气动和结构模型，在不可逆转地向计算资源消耗型的高保真模型发展；以此为基础的设计方法，如迭代/修正法、余量修正法、伴随方程优化法、耦合伴随方程优化法、代理模型优化法、智能优化法等，都尽量避免在计算资源消耗上进一步雪上加霜。而事实上，如前所述，目前国内已经具有很好的高性能计算资源，所以，有必要根据型号的实际需求，利用好这些资源，发展更有力的优化设计工具。

2018 年薛帮猛等人[18]在这方面迈出了一步。在“天河二号”上探索民机飞发集成复杂构型的精细优化设计，用遗传算法直接调用RANS 分析开展全局寻优的多目标优化，以期得到可靠的减阻效果。本文则进一步考虑机翼静气弹变形的影响，基于高保真气弹分析，以在超算上建立大规模设计变量(十万量级)的气动—结构综合优化方法为目标，开展相关工作。

1 优化方法

1.1 机翼外形参数化方法

基于描述几何外形的某种数学模型，采用有限个参数来控制机翼外形变化的方法，称为机翼外形参数化方法。在优化设计中，可认为是对设定连续设计空间的一种离散近似，它对寻优的质量和效率有着重要影响。作为它的基础，Guenov等人[19]对翼型参数化提出了完整性、正交性、无暇性、简约性和直觉性的评价要求。完整性指是否能按指定容差描述任何翼型；正交性指确保每个翼型与一套参数一一对应；无暇性要求参数化方法不会生成不良外形，诸如交叉的或退化的翼型；简约性指翼型主要几何特征产生显著变化只需少量参数；直觉性要求与参数物理意义相关，可简化输入界限选择或设计判断。

尽管目前已有很多参数化方法，但似乎还没有一种按这五条标准来看都是完美的。仅就完整性而言，Rendall等人[20]用2 174 个翼型测试了七种参数化方法；其中构造类方法纯粹根据指定参数描述外形，测试了CST、B样条、PARSEC三种；变形类方法基于已有外形变形生成新外形，测试了Hicks-Henne鼓包函数方法、RBF域元法、Bezier面的FFD方法和SVD模态提取法四种。该研究发现，这七种方法按Kulfan 的容差要求描述所有翼型需要20 个～25个参数，用13 个～18 个参数仅能覆盖其中80%的翼型。也就是说，这些参数化方法的完整性与其简约性就不能两全其美。由此推测，增加参数数量有利于增大参数化方法对设计空间的覆盖能力，可能促使优化要向大规模变量方向发展才更有潜力。

国内目前翼型优化大多用二维CST方法参数化，而机翼优化大多用FFD方法。考虑到不仅要用机翼平面参数和尽量多的型面参数，而且要有较好的无暇性、直觉性。本文应用三维类别函数/形状函数变换方法[21]CST(Class-function/Shape-function Transformation)定义机翼。

设(x，y，z)为机翼表面流向、展向和纵向的右手系笛卡尔坐标，用下标U，N，T分别表示上翼面、前缘点和后缘点。再设b为机翼展长，用c、xN、αTW表示某展向位置的弦长、前缘点流向坐标和几何扭转角，则翼面无量纲的流向和展向坐标(Ψ，η)可定义为：

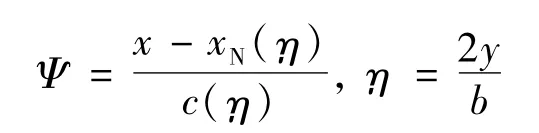
这时机翼上表面的纵向坐标可表示为(下翼面类似)：

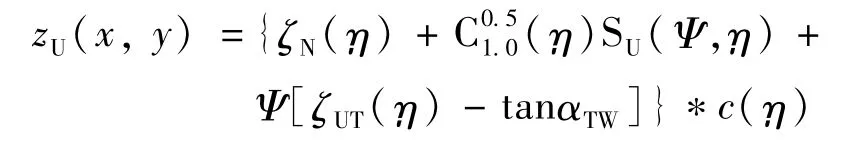
其中，机翼当地无量纲切向位移(计当地前缘点，描述机翼上反)：

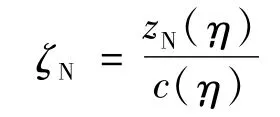
机翼当地无量纲后缘半厚度：

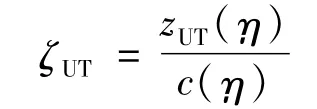
类别函数定义为：

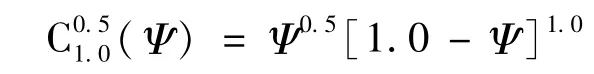
形状函数定义为：

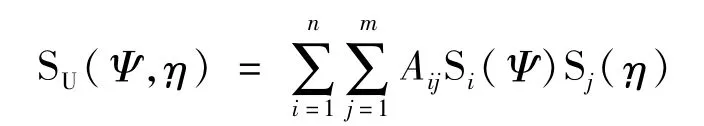
这里系数Aij(i=1，…，n，j=1，…，m)是待求的参数，以后用作控制翼面形状的设计参数。Kulfan的CST方法里Si(Ψ)和Sj(η)是Bernstein 多项式，可写成(二者类似写一个，下同)：

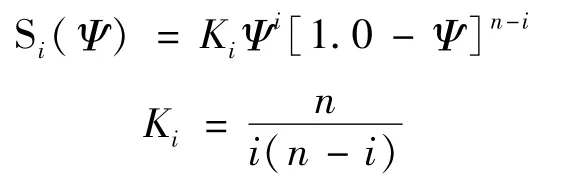
参数化描述气动外形，考虑到优化中的计算开销，一般希望参数Aij的个数尽量少。但有时担心如此约束了设计空间，妨碍寻优，又希望参数个数多一点，即n，m的取值大一些。这时采用Bernstein 多项式的次数高，描述的外形会存在比较大的波动。因为形状函数的定义就是张量积Bezier曲面，所以本文推广一下，采用递推定义的B样条基函数[22]Ni，p(Ψ)来描述Si(Ψ)和Sj(η)，把形状函数定义成B样条曲面，这样能大幅改善参数数量比较多时带来的波动问题。即：

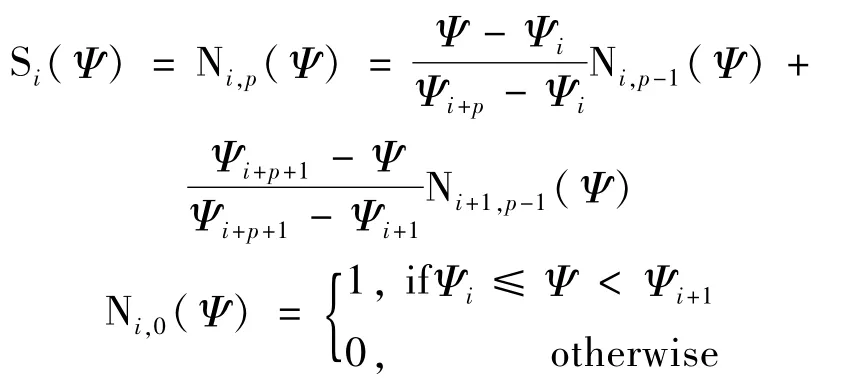
其中，p是流向Ψ方向曲线可指定的次数，另设q为展向η方向曲线可指定的次数。Ψi是根据原剖面点定义的节点，定义同前，但首末要取重节点以保持原CST方法控制前缘半径和后缘船尾角的能力。Aij可用作设计参数，在原CST方法里来源于Bernstein 基函数的最大值特性，但它的影响仍是全局的。改用具有局部支承性的B样条基函数，Aij的影响本质上是局部的。与本文的替换方式不同，van Tooren 等人[23]用B样条基函数与Bernstein 基函数相乘来拓展CST。

用以上方法进行机翼参数化描述，需四个平面设计参数，包括：机翼面积、展弦比、根梢比、1/4弦线后掠角。上反、扭转分布至少要在翼根和翼梢指定两个参数以实现线性分布，对一般的非线性分布可用简单的曲线参数化来描述，数量可定制。在指定较低的流向和展向的曲线次数(即p，q)后，给定若干展向站位的翼剖面数据，可拟合出型面设计参数Aij，拟合精度随n，m增大迅速改善。

图1 显示，针对CRM机翼采用以上方法在p=3，q=1 时，当m＞18，n ＞11 后表征拟合精度的最大残值Rmax才不大幅下降，以英寸为单位的全尺寸外形坐标可精确到千分位。图2 给出某个Aij取值变化对机翼上表面外形的影响，具有B样条曲面很规范的局部特性。图3 是在固定机翼面积下变化展弦比和1/4 弦线后掠角的效果，结合图2，展示了三维CST参数化方法既能修改机翼平面参数也能修改型面参数的能力。

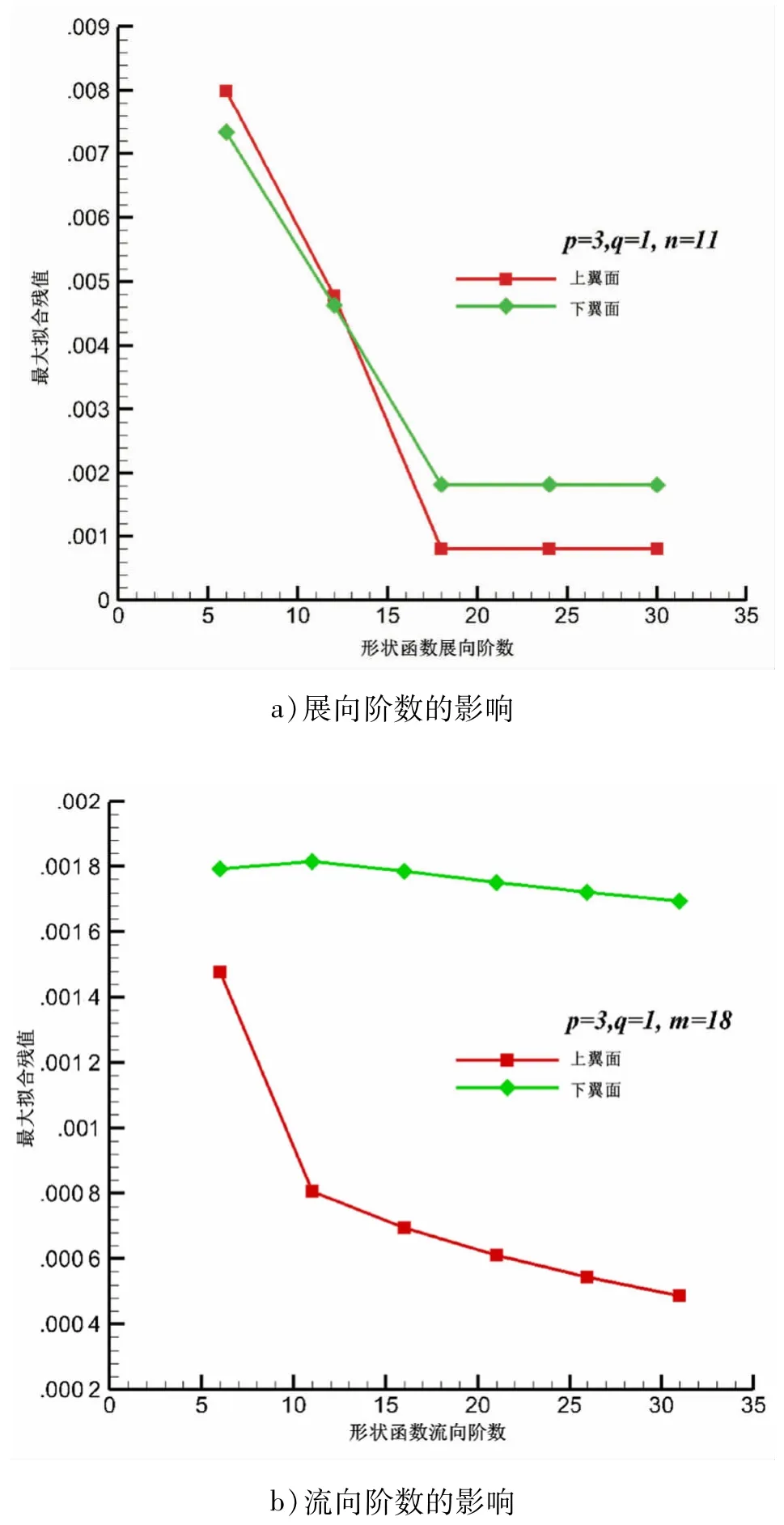
图1 型面参数数量对拟合精度的影响

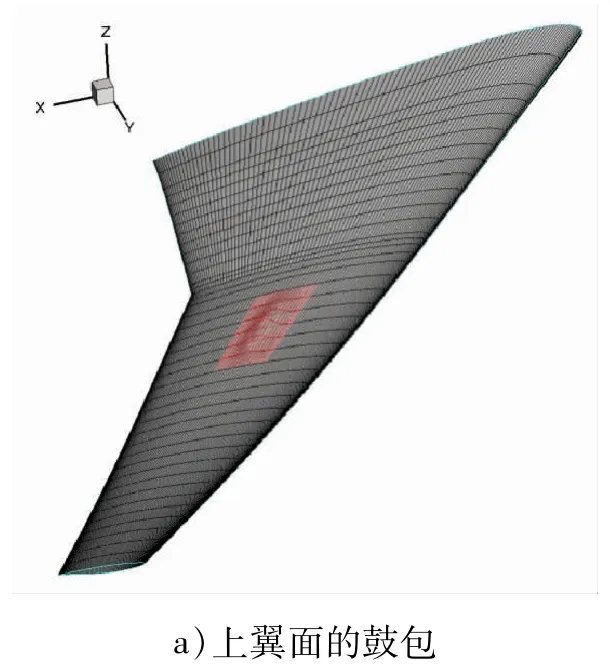
图2 型面参数变化的影响

图3 平面参数变化的影响(固定面积)

1.2 静气动弹性的CFD/CSD耦合分析方法

静气动弹性的CFD/CSD耦合方法可分成强耦合(联立求解CFD和CSD方程)与弱耦合(分开求解CFD和CSD方程，在界面交换信息)两类，国内似乎没人发展强耦合方法，尽管比较困难，但对柔性大变形问题这种方法可能更有利。弱耦合又可分成紧耦合(CFD和CSD方程迭代求解过程中交换信息)与松耦合(CFD和CSD方程迭代求解收敛后交换信息)两种，国内以紧耦合居多，不仅耦合时间精度高还可用于动气弹计算。

2006 年徐敏等人[24]建立的那种CFD/CSD耦合分析方法，很像是界面信息传输采用守恒体积转换(CVT)方法的松耦合。2009 年杨国伟[25]介绍的进展是结构运动方程和气动主宰方程的紧耦合，同时还介绍了基于虚功原理的两种气动—结构数据插值技术IPS 和RBF，以及三种动网格方法：适合多块结构网格中小变形的TFI方法、需要迭代求解的非结构网格弹簧网格平衡法、适用大规模网格基于背景网格的高效变形方法。2013 年张伟伟等人[26]从变形能力、变形质量和变形效率角度，重点总结了物理模型和数学插值两类的六种网格变形方法，并介绍了其在使用RBF进行网格变形和流固耦合界面数据传递上的收益，建议关注混合方法、网格变形算法的并行化等。2018 年杨超等人[27]对气动弹性分析中使用的气动力方法进行了综述，指出“满足工程气动弹性设计的需求，特别是对于大柔性飞行器的全机气动弹性问题”，CFD/CSD耦合要解决与飞行力学、结构动力学及飞行控制等的多学科耦合计算方法和效率问题。这对应用超算提出了需求。

本文采用的静气动弹性CFD/CSD耦合分析方法中，多块结构网格变形采用孙岩等人[28-29]发展的RBF和TFI混合方法，耦合数据传递采用TPS 方法，自主开发的CFD软件TRIP与CSD的紧耦合测试验证，详见孙岩等人2017 年的介绍[30]。对所用动网格技术，王运涛等人[31]在“天河二号”集群上开展了十亿量级网格变形的并行效率测试，对1.8 亿网格的CRM-WBH构型及其风洞试验模型的有限元模型，开展了静气动弹性模块并行效率及一致性测试，都取得了良好结果。值得再提的是，应用这套方法及软件，王运涛等人[32]确认包含支撑装置和静气动弹性变形的CRM-WB构型气动特性数值模拟结果，可以更加接近试验结果。

需要指出的是，不同于前述文献用柔度矩阵方法或结构模态分析方法去计算机翼静气弹变形，本文CSD分析直接采用SiPESC.FEMS 软件进行有限元计算。SiPESC是大连理工大学工业装备结构分析国家重点实验室自主开发的“工程与科学计算软件集成平台”，其中的开放式结构有限元分析系统FEMS 是一款可与NASTRAN对标的自主软件。直接采用有限元计算可能更有利于柔性机翼的静气弹大变形计算，与CFD软件TRIP耦合，对非线性气动力的情况也有较好的适用性。

1.3 优化算法

针对十万变量的超大规模优化问题，智能寻优算法存在“维数诅咒”，难以应用。所谓大规模的智能寻优算法，变量规模大多在一千或二千以下[33]，超过五千变量的极少。文献[34]的合作协同进化算法对一些五千变量的测试函数进行优化，函数计算次数高达百万量级。西安电子科大公茂果等人2005 年左右发展的免疫遗忘克隆规划算法[35]，对一些超高维(一万)测试函数的优化，函数调用次数降到了十二万量级；而且估计若更高维使用其算法，函数维数每增加一维，函数计算次数平均增加接近25 次。由此估计十万变量的优化也需要两百多万次函数计算。若这些函数调用换做费时的CFD计算，即便使用超算恐怕也难以胜任，所以针对这种问题，使用智能寻优算法必须想办法降维。

优化过程中不直接调用CFD软件计算，而通过模型来预测，可减少计算量，即所谓基于代理模型的智能寻优算法。其主要计算开销集中在建模需要的样本计算上，增大设计变量的数量规模对构建代理模型也是一项挑战。一方面，随设计变量增多，建模需要的样本规模迅速增大；广泛采用的拉丁超立方采样(LHS)，为保证均匀性一般也要求样本规模至少大于变量维数，样本规模越大均匀性越好，需要开展的CFD计算也越多，这对应用超算进行大规模并行计算提出了需求[36]。王超等人[37]在70 个设计变量的翼身组合体等气动优化问题中构建支持向量机模型，发现在同为1 000 的样本规模下，采用高维模型表示方法(HDMR)比采用LHS 得到的模型预测精度更好。似乎可以推断同等模型精度要求下，HDMR方法的样本规模可以更小，即使如此，估计样本规模也要比变量维数大一个数量级以上。

另一方面，就算能完成这种大样本计算，高维数据的建模也是一种挑战。当然这主要指构建数据驱动的代理模型，包括气动优化领域广泛采用的参数模型(如响应面模型、径向基模型)和非参数概率模型(如Kriging模型、高斯过程回归模型)等各种数据拟合模型及降阶模型(如基于正规正交分解的POD模型)，都存在维数灾难。近年来，各种高维统计降维方法的应用，BP神经网络和支持向量机(SVM)的各种改进，甚至深度神经网络(DNN)等大数据学习方法的流行，使得高维数据建模技术迅速发展。但所谓的高维建模，就作者所看到的而言，建模的变量数很少有超过二、三百的，而一个典型的气动优化问题设计变量大致在20 个～1 000 个左右[36]，差距是有的。所以，再考虑到样本计算的成本，基于物理的代理模型[38]可能更有前途，虽然适用范围不如数据驱动模型宽，但可能更适合气动相关领域的超大规模优化需要。这类模型指高效的低阶预测加修正/增强技术，即用简化物理模型或稀化计算网格预测，其结果与高保真预测的差量用与维数无关的修正/增强技术改善；故有人又称之为启发式模型或多可信度、变可信度或变复杂度模型。

智能寻优算法在超大规模优化中存在的困难，好比“优化十个设计变量需要五千次函数计算”，为此本文选用梯度寻优算法，以期“优化五千个设计变量仅用十次函数计算”。但传统梯度寻优算法的计算开销与设计变量的数目仍然相关，虽然相对弱些，但还存在所谓的“扩展问题”。假设设计变量数目为N，Jameson 等基于最速捷线问题的优化研究，估计[39]最速下降法(具有整体收敛性；线性收敛速度)的计算开销为O(N2)，伪牛顿法(对凸函数具有整体收敛性；二次终止性，超线性收敛速度)的为O(N)，N很大的话，优化过程将非常漫长。Jameson提出的伴随优化方法之所以高效，不仅因为消除了梯度计算量与设计变量数的相关性，而且还有一项关键，即使用Soblev梯度消除了寻优算法对设计变量数的相关性[39]。所以，不能认为解决了梯度计算量问题，用任意多设计变量做大规模优化就畅通无阻了。

在工程大规模优化研究领域，Vanderplaats应用其软件产品BIGDOT在2002 年完成了5 万变量和5万约束的优化验证[40]，实现了超过13.5 万个变量的结构无约束拓扑优化，可能是航空工程领域提倡十万变量优化的源头，国内相同规模的结构优化见罗利龙等人2016 年工作[41]。Vanderplaats从可靠性、效率和内存需求角度评估了一系列新老算法之后，在BIGDOT中采用了受专利保护的改进SUMT外点法[40]处理约束、FR共轭方向用作搜索方向、多项式插值进行一维线搜索，这套算法的函数和梯度计算次数不随设计变量数量增加而显著变化，具有很好的扩展性。其经验表明，进行超大规模的约束非线性工程优化，算法要在保证可靠性的基础上，削弱计算开销与设计变量的相关性。即减少内存需求和避免耗时的子优化或优化方向计算。

因此，本文贴近工程应用的静气弹优化，考虑其计算开销较大，不追求优化解的精度，选用整体收敛性较好的一种改进最速下降法[42](SD with BFGSpreconditioned)，它对初值的依赖性较弱，用不多的内存开销，对寻优方向进行一种预条件处理，图4给出了该算法对某测试函数在十万变量下，与设计变量数目无关的优良收敛特性。结构尺寸优化的特点是变量和约束多，计算开销相对较小，选用该领域发展出来并流行的移动渐近线方法[43](MMA)。该方法构造并求解一系列可分离的子优化问题，这些子优化问题是原目标和约束函数的显式单调严格凸近似，与设计变量数目无关、收敛性可调是MMA最为显著的优势。在此基础上发展的序列凸规划法(SCP)，用于超过百万维的结构拓扑优化已得到验证[44]。

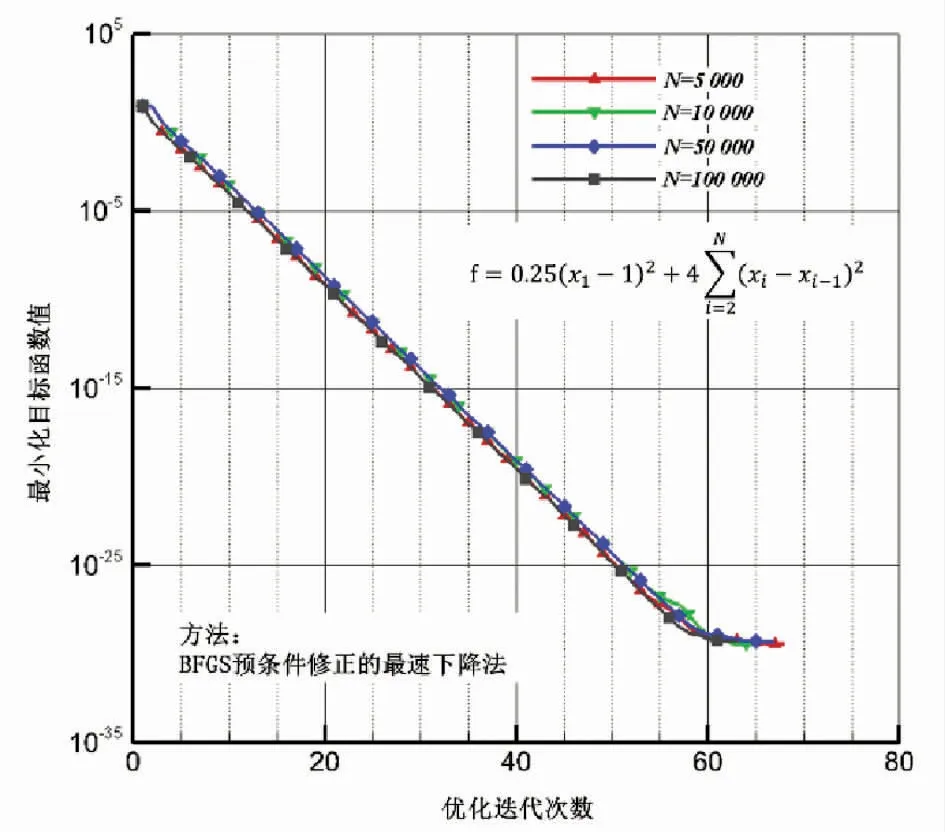
图4 测试函数最小化收敛历程

1.4 设计敏度计算方法

敏度分析研究模型的输出如何随输入的变化而变化，主要用于基于梯度的优化、不确定度量化、误差分析等[45]。它有全局敏度和局部敏度之分；全局敏度分析在更为宽广的取值范围，量化相对输入的输出响应，适合于有较大不确定度的模型；而局部敏度分析针对固定的一套输入，量化输出响应，用于高确定度的物理模型。这里将CFD和CSD计算程序视作确定性模型讨论局部敏度计算，偏导数计算是敏度分析的主要内容，应用中对二者大多不加严格区分。

对由计算机程序定义的函数，其导数计算目前有三类方法：数值微分、自动微分和解析方法。数值微分原理上基于泰勒级数展开做近似计算，存在截断误差，用函数值或函数其它信息估算导数。主要包括有限差分法和复数步方法两种，计算量都与设计变量数目相关。有限差分法估算导数的精度依赖扰动步长的选取，减小截断误差需要减小扰动步长，但一直减小扰动步长会增大减法抵消误差(相近数相减带来的有效数字损失)，对每个设计变量存在一个平衡这两种误差的最优扰动步长。这种方法大多用在把计算模型当做“黑箱”的情况，是梯度类优化软件的缺省设置(如采用SQP方法的SNOPT)，当函数计算存在噪声时(来源于糟糕的收敛特性或网格变形)，足够大的扰动步长有平滑作用，可抓住函数变化的正确趋势[45]。复数步方法用复变量计算实函数的导数，需要修改计算模型的源程序，可用于任何算法以及高阶导数计算，国外的应用日益增多。因为没有减法抵消误差，扰动步长可以小到机器零，几乎消除了截断误差，使得导数的计算精度与函数本身的计算精度相当，自然比有限差分方法高。Martins等人[45]认为复数步方法本质上可以看成用运算符重载的自动微分，在极限上即扰动步长为零时，可得到与自动微分方法相同的导数；而在实际有限精度的算法中，只要扰动步长足够小，就可得到相同的结果。

自动微分(AD)也叫算法微分或计算微分，是一种基于微分链式法则，对计算机程序逐行进行求导的技术；与解析方法对数学表达式求导类似，但要用专门的软件工具(如ADIFOR和ADIC等)改造源程序。因为没有截断误差，能得到与解析方法同样准确的结果，但可自动执行更为简单。自动微分有正向、反向两种计算模式，计算量分别与设计变量数目、目标函数数目相关。但像复数步方法一样需要更多的内存和计算的开销，比有限差分方法更为耗时。自动微分方法计算的导数最为准确，可用于解析方法中近似计算导数的精度校核。

这里所说的解析方法，需要把计算机程序采用的算法返回到数学表达式上，再用链式法则等方法推导，最后编成程序进行计算。期间可采用符号微分软件工具如Maple、Mathematica等，但更多地需要手工操作。这种推导要么在连续的微积分表达式上进行，要么在离散的代数表达式上进行，都带来两类导数计算方法：直接法和伴随法。前者导数计算量也与设计变量数目相关(但解的是线性方程，不同前述解非线性方程)，在目标(或约束)函数比较多时效率高。后者相反，导数计算量仅依赖目标(或约束)函数的数目，在设计变量比较多时效率高。典型气动外形优化问题的变量多目标少，选用伴随方法计算导数效率最高。在某些结构减重的尺寸优化中，设计变量和目标(或约束)函数的数目可能相当，而且数目都很大，这两种方法的优势都不突出，常用聚合约束减少其数量的方法放缓了优化收敛历程，需要发展新方法[45]。解析方法求导数比较复杂，需要详细掌握计算模型采用的算法，编程调试开发时间也比较长。但因为计算机条件的限制，开发这种高效率计算方法的人还是很多。

理论上，解析方法求得的导数，其数值精度与原算法相同，而实际上没有如此乐观。主要原因是总导数即设计敏度的数学表达式可以解析推导出来，但是其中具体的各项偏导数并不是都能解析推导出来的，如通过交互操作生成的飞机复杂外形CFD计算网格相对设计变量的导数等等。绝大多数的解析方法，用有限差分法计算这些偏导数，Dwight等人[46]认为这是敏度误差的主要来源，要提高计算精度，需要对每个设计变量逐个寻找有限差分法计算用的最优扰动步长。这是件非常繁重的工作，通常统一采用一个步长，由此带来误差。此外，在连续伴随方法中，不是对任何目标函数，都能得到连续伴随方程的适定边界条件：1)有可压缩间断时，推导连续伴随方程存在连续可微的理论假设问题；2)RANS 的连续伴随方程推导，忽略了湍流模型的影响；3)数值求解连续伴随方程，存在离散一致性问题；4)伴随敏度的网格收敛性问题等等[46]。在离散伴随方法中，控制方程左端项雅克比矩阵影响敏度计算精度，其完整、准确的推导是件极其繁重的工作，引入简化近似假设会给敏度计算带来误差[46]。如大多数工作冻结涡团黏性系数，忽略对湍流模型方程的线化，带来了误差，有些工作对各种湍流模型输运方程进行了线化处理，但可能使最后迭代求解的线性方程条件数变差，带来收敛问题。Dwight等人还列举了离散伴随方程推导中，带来误差的其它一些近似方法[46]，包括：忽略对流项中人工耗散系数的导数、线化时仅使用一阶对流通量、线化简化的黏性通量、完全忽略黏性项以及最极端的做法，敏度计算中彻底忽略气动的贡献，只有网格相对设计变量导数的影响，等等。用基于这些近似推导的雅克比计算的敏度与准确结果相比，有些相对误差可高达90%，以致于是否可用受到质疑。

复杂解析方法的敏度计算精度评估，大多根据其计算结果与有限差分方法结果的对比情况进行判断，但是后者作为标准也受质疑，所以有人在稍小的问题中，采用复数步方法或AD方法的计算结果作为评估标准。敏度在优化算法中当作梯度用于构造寻优方向，其精度对优化的速度和精度有重要影响，越高越好。然而，Dwight等人[46]指出，对一些健壮的优化算法，如共轭梯度法和最速下降法，用一些精度较差的敏度(各种近似的离散伴随方法的结果)，在数量相当的迭代步数内，也能得到与用高精度敏度相同的优化结果，但对BFGS 伪牛顿算法则不行。也就是说，离散伴随方法中雅克比的大多数近似，是否可用与问题相关，在对敏度计算精度没把握时，采用简单健壮的优化算法是有利的，这同前述解决大规模优化问题的指向一致。

在设计敏度的计算上，为避免有限差分法带来的计算量问题，过去三十年里，先是以连续伴随方法的研究为主，后来离散伴随方法的研究增多。二者都能给出满足需要的敏度精度。因为典型伴随敏度的主要误差来源是计算网格相对设计变量的导数，所以连续和离散哪种方法更好，取决于具体推导和编程实施[46]。目前AD技术在离散伴随方法偏导数的计算中取得了特别好的效果[45]，二者的深度结合可能是一个发展方向[46]。

然而，高性能计算技术的提高，尤其在E级计算环境下，设计敏度有限差分法计算量的问题，即使在工程应用上，也可以预期将大为缓解。首先，CFD分析已广泛采用大规模并行计算；其次，设计敏度用有限差分法计算，相互间没有信息交换，完全可以通过并行计算缩短时间[36，47]。虽然计算效率较低，没有在理论上解决敏度计算量相对于设计变量数目的扩展性问题；但是可把各种软件当做“黑箱”，只有一个简单地步长优化问题，上手快，应用简便灵活，适用范围广，特别适合工程多学科问题。原来在串行计算环境里，采用差分敏度方法，计算时间过于冗长，但在目前及以后的大规模并行计算环境里，资源不是大问题，敏度计算时间完全可以缩短到一遍流场计算时间的量级，情况与原来有了很大不同。相比发展复杂的气动-结构耦合伴随敏度计算方法[48-49]，差分敏度更易在短期内得到成功实施。为此，本文在气弹并行计算软件的基础上，采用并行的有限差分方法计算设计敏度。

2 优化问题描述

高速大展弦比机翼的典型优化设计问题是最大化航程/航时。除发动机耗油率外，主要涉及气动和结构两个学科，需要气动效率最大化，结构重量最小化。二者对机翼展向载荷分布、展弦比、相对厚度等参数的要求迥异，需采用优化技术来定量协调。目前这两个学科各自的优化设计技术都很成熟，希望进一步提高设计技术的能力，必须在设计初期进行学科综合，以期获得整体最优的协同效应。然而，各学科自身的优化设计问题，已是一个复杂的多目标多约束的非线性优化问题，如何综合存在挑战。例如，气动外形优化要在来自结构设计的厚度、容积等几何约束下，最大化巡航设计点的升阻比，最大化起降设计点的最大升力系数，还要在巡航马赫数下满足对抖振升力系数、俯仰力矩系数的约束，以及巡航升力系数下对阻力发散马赫数的约束，等等。结构尺寸优化，就机翼减重而言，要考虑各种机动、阵风、滑行等多种载荷下的强度、刚度、疲劳寿命和可靠性等要求，还要考虑来自静/动气弹分析的稳定性约束。把两个学科实际设计目标和约束过度简化/忽略的综合优化，实用价值可能受限。

为充分发挥各学科的专业优势，本文采用学科分治的思路进行综合优化，同时也贴近工业部门的组织分工和设计流程。技术实现上做了三件事：1)气动外形的参数化模型和结构有限元的参数化模型，适时匹配(见图5)，方便载荷、变形信息的准确交换；2)基于该匹配模型，用TRIP+SiPESC耦合软件计算静气弹平衡的气动力和载荷，分别用于气动优化和结构优化；3)气动优化输出的匹配模型及其对应的机动载荷，是结构优化的输入，后者更新有限元模型的尺寸属性再返回气动优化，之后循环直至收敛。形成的综合优化框架如图6 所示，其中左右两边分别为气动优化和结构优化，中间是有限元模型与气动外形的匹配合成，通过它及耦合静气弹计算实现两学科优化的综合。

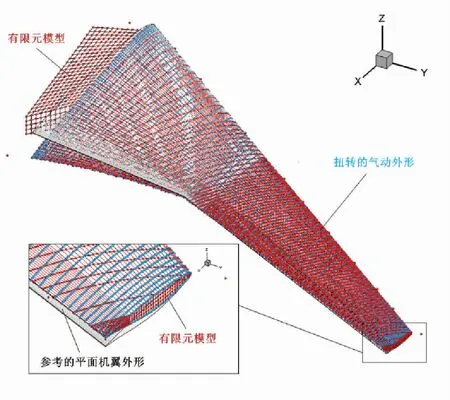
图5 有限元模型与气动外形的匹配

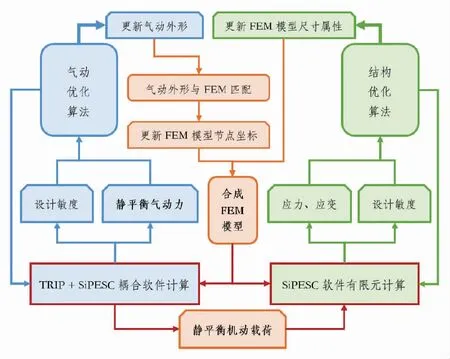
图6 气动结构综合优化框架

这样进行气动-结构优化的综合，不仅可以发挥各学科做细做实的专业优势，而且有利于各学科根据自己问题的特点，选用合适的优化算法，更有效地解决问题。而不是笼统地采用一种优化算法，给困难的非线性约束优化算法平添更多麻烦。比较而言，气动优化的特点是函数计算开销大，结构优化的特点是变量和约束多。所以，这里气动优化用无约束优化算法，其中几何约束在参数化建模时实施，不对违反约束的外形进行CFD计算，减少计算开销，来自各设计点的设计目标，采用线性加权的评价函数方法，转化成单目标优化问题减少计算量。而结构优化则用大规模变量的非线性约束优化算法，可对有限元模型每个单元提出设计变量和约束，采用静气弹平衡的气动载荷，而不是其它大多数工作采用的刚体外形气动载荷，理论上可使结构优化更为精细可靠。如此，也实现了设计变量的分组，缓解了大规模设计变量带来的困难。

2.1 气动优化问题

选用NASA的CRM 标模[50]机翼作为研究对象。这款公开的标模具有跨声速远程宽体民机的典型气动设计特征，不仅提供了机翼巡航时的名义1-g外形，还提供了相应的结构有限元模型。其巡航设计点为：

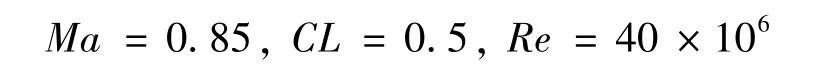
原始机翼的参考面积(Wimpress面积[50])为4 130 ft2(1 ft=0.304 8 m)，参考弦长是不考虑Yehudi的梯形翼平均气动弦长275.8 in(1 in=0.025 4 m)，力矩参考点取该平均气动弦长的前1/4 弦长点。该梯形翼四分之一弦线后掠角为35°，展弦比为9.0，梢根比0.275。原始机翼展长b 为192.8 ft，翼身交接在10%*b/2 附近，37%*b/2 站位为后缘Yehudi拐折。展向有21 个定义截面，除拐折外其余按5%*b/2 的间隔均匀分布；由缩比模型后缘厚度不能小于0.014 in 的制造约束，导出翼尖后缘相对厚度为0.48%c(c是当地弦长)。CRM外露翼的截面最大厚度，翼根10%*b/2 处约65 in，拐折37%*b/2 处约30 in，翼尖约10 in，最大相对厚度分别为13.8%、10.5%和9.5%。CRM外露翼的截面最大相对弯度，翼根10%*b/2处约为0.1%，拐折37%*b/2 处约为0.95%，并开始采用超临界翼型；大的弯度集中在60%*b/2 到90%*b/2 之间，其最大相对弯度在1.5%到1.6%之间，之后往翼尖降到0.09%。

CRM机翼展向几何扭转角，总的外洗超过8°。有两段大的扭转，估计用于改善失速特性，见图7 所示，一段从翼根的4.44°降到拐折附近的0.76°，另一段在翼梢，从90%*b/2 附近的-2.57°降到翼尖的-3.75°，两段之间布置的超临界翼型外洗在2°以内。根据这个特征，定义了4 个设计变量来控制几何扭转分布，即图7 中的DV1～DV4。对CRM模型名义1-g外形来说，以上几何扭转包含了静气弹变形。机翼上反方面也包含了静气弹弯曲，相对翼根前缘点，翼尖前缘点非线性地向上抬起了约88 in，相当于7.6%的半展长高度，估计在线性静气弹的变形范围。

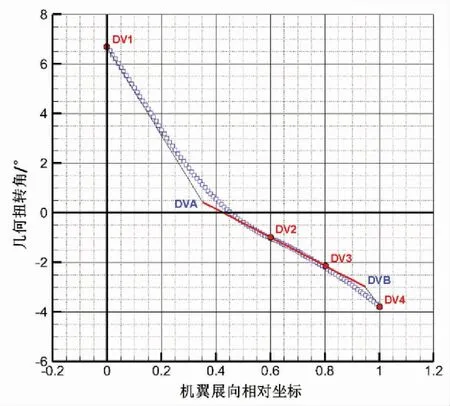
图7 机翼几何扭转分布的设计参数定义

图8 给出了CRM机翼无弯扭的平面机翼。本文假设它是初始型架外形，期望通过优化得到其展向几何扭转分布，叠加上气弹扭转变形，满足巡航气动效率最大化。在前述设计点的固定升力系数下，最小化选用的目标函数为：

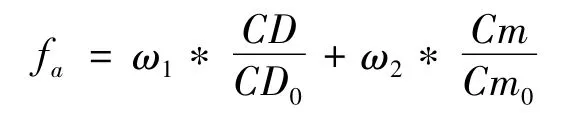
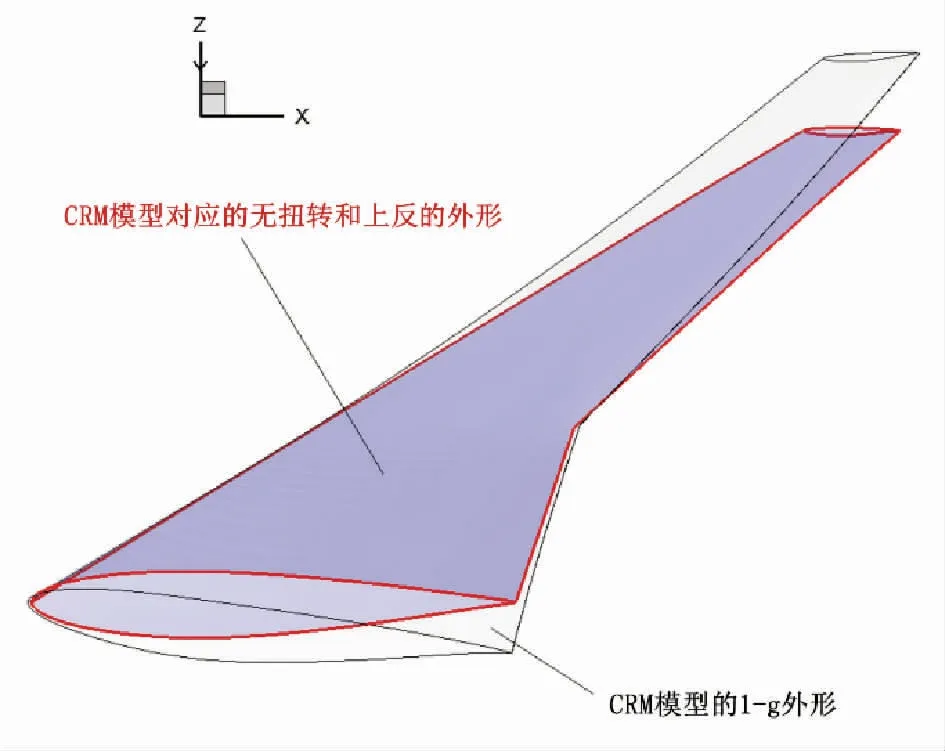
图8 CRM机翼参数化无弯扭外形与1-g外形对比

其中ω1，ω2为权因子，CD，Cm分别为阻力系数和俯仰力矩系数，CD0，Cm0是这两系数的初始值，用于规范数值大小。这里引入俯仰力矩系数旨在减小配平对气动效率的影响。

包括阻力系数和俯仰力矩系数在内的气动力系数，通过气弹耦合程序TRIP+SiPESC计算得到。其耦合方法前文已介绍，在CFD方面，TRIP采用SA湍流模型计算全RANS 方程，对流项离散采用MUSCL-Roe方法，时间推进用隐式LU-SGS 迭代。气动系数的无量纲参考量和力矩参考点与CRM机翼一致，不再赘述。

2.2 结构优化问题

以NASA的CRM-V15-wingbox-1.bdf全尺寸半展长翼盒有限元模型(FEM)为基础，其结构布局是标准设计手册提供的传统方案，包括两主梁和蒙皮，以及50 多翼肋，以及桁条、翼肋缘条和加强筋等部件。首先，考虑气动载荷的传递需要，在前后缘操纵面区域添加了模拟蒙皮和翼肋的面单元，替换原来的刚体单元RBE3 和集中质量单元CONM2，如图9 所示，然后，根据前述气动模型除去弯扭建立的表面外形，调整节点坐标与气动翼面一致。整个FEM模型有20 451 个节点，42 477 个单元，包括12 980个简单梁单元CBAR、29 470 个四边形板单元CQUAD4 和少数三角形板单元CTRIA3 三类。原CRM有限元模型材料采用各向同性的铝合金，杨氏模量E=10.3 ×106psi，密度ρ=0.101 lb/in3。翼根有位移约束的节点分布如图10 所示，是有限元计算的固支边界约束。气动载荷加载位置的分布如图11 所示，做静气弹的线性分析，作用力的方向假设不变。加载的2.5-g气动载荷通过气弹耦合程序TRIP+SiPESC计算得到，计算条件是：

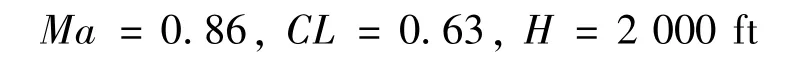
图9 前后缘替换刚体和集中质量单元(红)的面单元

图10 翼根位移约束节点的分布

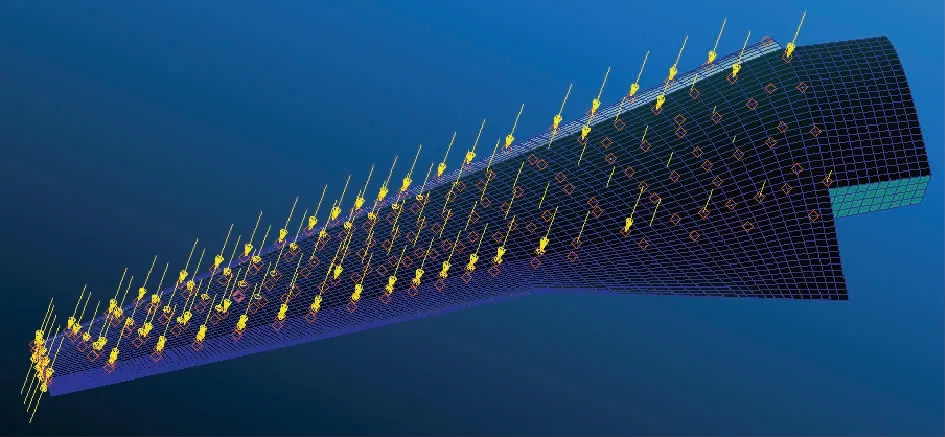
图11 气动载荷加载位置的分布

结构尺寸优化设计参数，计划取壳单元属性PSHELL的厚度参数，以及梁的截面尺寸参数，后者影响梁单元属性PBAR的面积、惯性矩等等。本文取了10 000 个四边形板单元CQUAD4 的壳单元属性PSHELL中的厚度参数，作尺寸设计变量。优化约束是最大应力和最大位移，通过有限元计算软件SiPESC.FEM 得到，它兼容商业软件NASTRAN的bdf输入文件格式。最小化结构重量为优化目标，密度不变情况下，通过体积计算值表征。

3 初步优化结果

虽然基于梯度的优化算法比无需梯度的算法难用，但对设计变量在O(102)量级或更多的优化问题，它们是目前唯一的途径[45]。然而，对气动—结构两学科、甚至更多学科的复杂耦合系统来讲，设计敏度的高效计算也是一件困难的事。除发展先进的算法外，利用超级计算机提供的高性能并行计算能力，也是一种不应该被忽视的解决方案，为此，本文提出采用差分敏度并行计算策略代替早年的串行计算方案。为证明其可行性，这里采用小规模的优化设计算例验证。初步以CRM单个机翼而不是翼身组合体为对象，减小CFD网格规模(单独机翼500万左右)和计算时间，便于调试。初步以钢作为结构材料，其杨氏模量为E=30.5 ×106psi，避免铝合金在2.5 g载荷下变形大带来的几何非线性问题；因为本文采用静气弹计算的可靠性，目前还局限在线性变形范围内，希望最大位移控制在10%*b/2内，对CRM机翼来说为115 in，最大应力不大于材料的极限，估计为3.5E5 psi。初步以前述4 个展向几何扭转控制参数作设计变量，没有用更多的型面控制参数作设计变量去减小波阻，旨在减少计算量便于程序调试。初步以指定范围单元的最大应力、最大位移为约束，不对所有单元都提约束，降低对一万变量约束优化算法的挑战。

在气动中心计算所，采用六百个核耗时三天完成上述算例计算。图12 的气动结构两轮综合优化历程显示，在不降低气动效率，满足最大应力和位移约束下，实现减重9%，俯仰力矩系数改善近40%，验证了方法及软件的有效性。图12(a)说明1 g载荷静气弹优化过程中固定了升力系数。注意在一轮结构优化后，做第二轮气弹优化时升阻比不升反降。对比图12(b)可发现，第二轮气弹优化过程中，俯仰力矩系数绝对值在迅速减小。由于这里优化的评价函数是阻力系数和俯仰力矩系数的加权组合(ω1=0.8，ω2=0.2)，说明这时俯仰力矩系数绝对值的减小，主导了评价函数的减小。图12(c)给出了两轮2.5 g载荷下的结构优化历程。可以看出，主要的改善来自第一轮优化的前两步。图中也给出了最大应力、位移满足约束的数值。最大应力2.5E5 psi小于约束，最大位移83.9 in 也小于我们线性变形的位移约束。

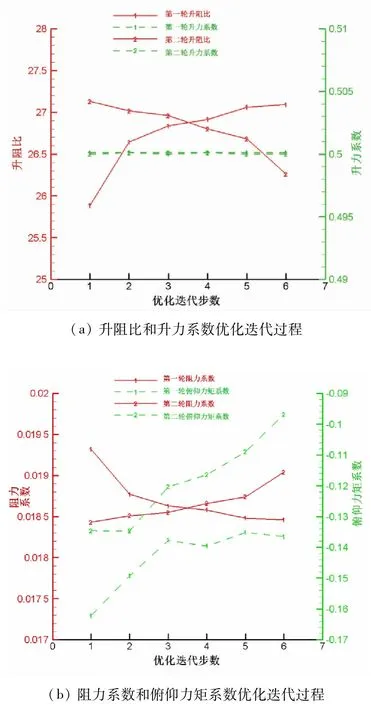
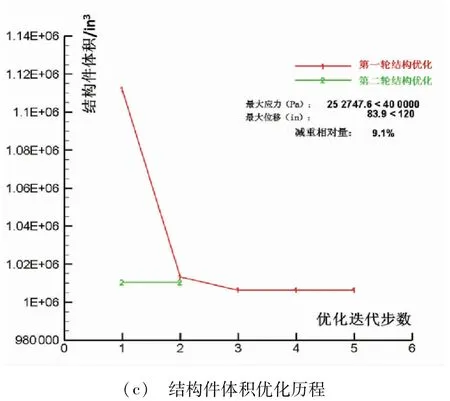
图12 气动-结构两轮综合优化历程

图13 介绍型架外形几何扭转优化后，得到的1-g静气弹变形情况。图13(a)展示了巡航设计点的表面压力分布，没有优化型面参数还存在激波。从图13(b)可看出这时翼尖有约40 in 的位移，是加载2.5-g载荷最大位移的一半左右，定性合理。图13(c)中红色曲线是1-g构型的几何扭转分布，它是型架外形几何扭转分布(蓝色曲线)和静气弹扭转变形(绿色曲线)的叠加结果。85%*b/2 处有近4°的外洗，与原CRM机翼相当。但向翼尖方向扭转角减小，与一般的扭转分布有些不同，这是由于本文定义的扭转设计变量DV3 和DV4(见图7)的敏度不同所致，似乎有些翼梢小翼的作用，用一个设计变量控制整个外段扭转可以避免这种情况。这里的扭转分布，在翼梢、翼根处与CRM机翼扭转分布差别较大，仅照顾了1-g飞行气动效率的需要，下一步需要在翼身组合体上，同时兼顾改善失速特性的需要进行优化。

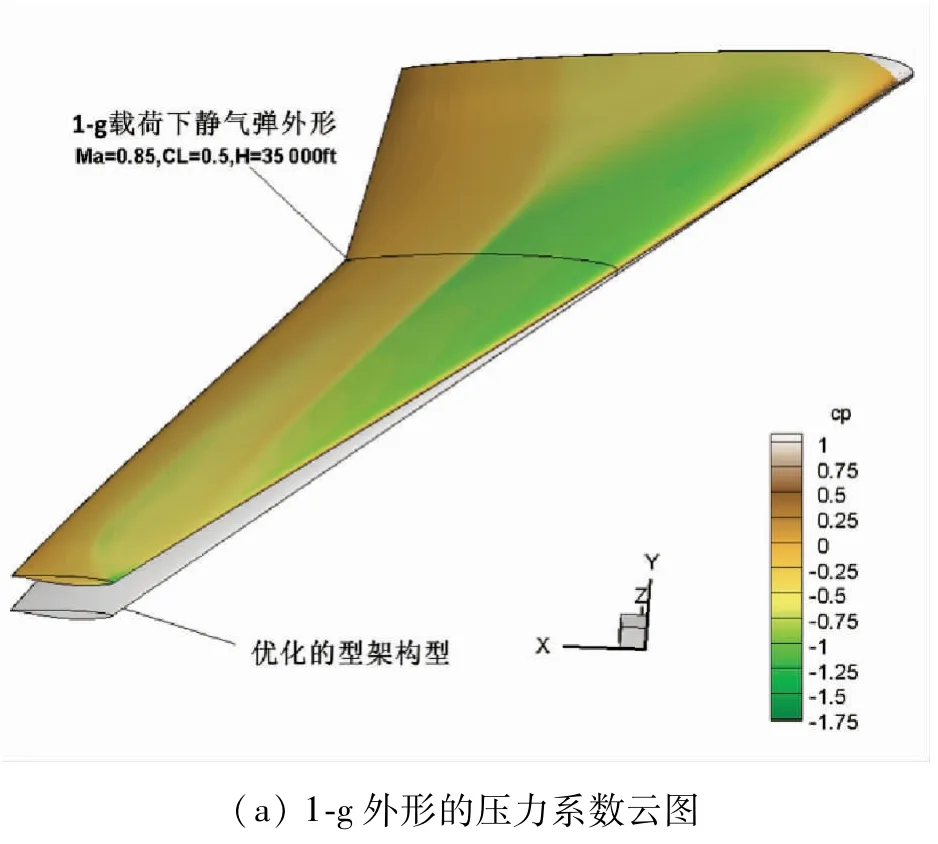
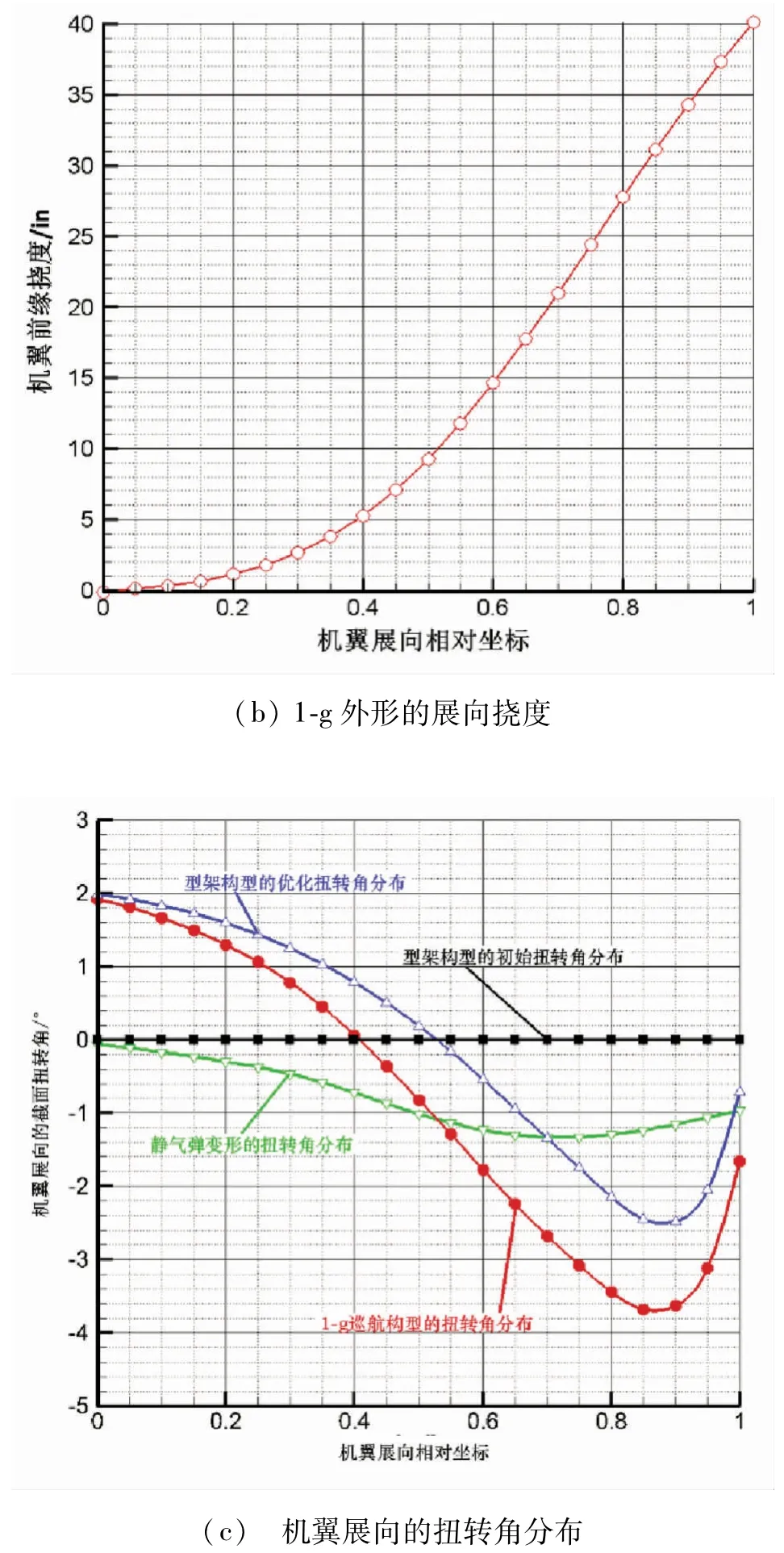
图13 巡航外形的静气弹变形

4 结论

面向工程应用的高保真静气弹优化设计，可采用先进算法实现，有高性能计算技术的支持，也可采用简单健壮的方法实现。通过本文基于CFD的优化方法介绍，围绕CRM机翼开展的稍小规模算例测试分析，可以得到以下两条结论：

1)差分敏度采用大规模并行技术计算，可避免原来差分敏度串行计算时间开销过大的问题，而与耦合伴随方法相当，进而快速解决气动-结构高保真耦合分析的敏度计算难题；

2)采用健壮的预条件最速下降法和移动渐近线法优化，不仅整体收敛性好，而且可使优化循环步数与设计变量数目无关，能避免大规模设计变量带来的计算开销过大问题。

本文基于TRIP和SiPESC软件建立的方法具备向更大规模气动结构综合优化发展的潜力。下一步，将应用已获得初步调试结果的几何非线性气弹计算代码，针对铝合金和复合材料机翼的翼身组合体构型，进行多点优化设计研究。