基于HJ-1A CCD影像和ELM模型的太湖叶绿素a预测研究

樊广利，曹红业，徐 晋

(1.西北大学 城市与环境学院，陕西 西安 710127； 2.西京学院 土木工程学院，陕西 西安 710123； 3.长安大学 地质工程与测绘学院，陕西 西安 710064)

1 研究背景

由于我国人口密度大和过度开采利用水资源，目前正面临极为严重的水资源问题[1]，并且内陆湖泊水资源问题目前己经成为全球性的问题，水质监测和预警是水质评估和污染防治的主要依据[2-3]。传统方法需要现场布设大量观察站点，具有耗时、劳动强度大、成本高的缺点，并且由于传统方法仅限于时间尺度和空间尺度，采集的数据只是部分河段的水质数据，只能以点带面研究整体情况。对于内陆湖泊这样的大面积水域，传统的野外采样-实验室分析方法难以达到大范围、迅速、长时间序列的动态水质监测要求[4]。特别是对于太湖等水环境时空异质性较强的水体，传统方法的不足尤为突出。

由于遥感技术具有长期、实时和快速的水质监测的优势，甚至可以较为精确地探究传统方法不可解释的污染蔓延趋势[5]。基于水体中不同材料成分的光谱反射率的差异，以及远程传感器接收的特征信息的差异，利用此技术可掌握大范围水域中不同物质组成的时空分布及长时间变化规律[6]。

叶绿素a浓度是反映水体藻类关键的生物指标[7-9]。然而目前对于水质较为复杂的内陆湖泊，建立适用性强、精确度高的水体叶绿素反演模型总是困难的。目前，主要有3种方法用于遥感监测内陆水域的叶绿素a浓度，即分析模型、经验模型和半经验或半分析模型[10-12]。

叶绿素a浓度的遥感反演是一个具有大量不确定性的非线性过程[13-14]。目前一些机器学习算法具有优秀的非线性近似等优点。被广泛应用于模式识别、特征提取、信号处理和非线性预测等领域，在水质遥感反演中具有一定的应用[15-22]。BP(back propagation)神经网络模型在水质参数反演等领域已经得到了很多应用，但是BP人工神经网络训练速度慢，参数选择困难，极容易陷入局部极值。极限学习机(extreme learning machine, ELM)是一种全新的单隐层前向神经网络方法的机器学习模型[23-24]。与传统的BP模型相比，ELM模型算法克服了传统模型训练时间长和过拟合等问题。同时，ELM的良好泛化能力也在实践中得到了验证。

环境一号(HJ-1)是我国首颗用于环境监测预警的遥感卫星，为水体叶绿素a浓度反演提供了巨大便利。但是目前利用HJ-1进行内陆水质监测的研究并不多，特别是水体叶绿素浓度遥感监测方面的应用更是较少。为了验证HJ-1卫星应用于内陆湖泊叶绿素a浓度预测的应用潜力，本文以内陆典型湖泊——太湖为例，基于ELM模型和HJ-1A CCD传感器进行太湖叶绿素a浓度的预测，并交叉对比传统BP模型和支持向量机(support vector machine, SVM)模型。同时，将ELM模型应用于大气校正后的HJ-1A影像上，获取整个太湖湖面叶绿素a浓度的空间分布图，并细致分析反演结果以验证模型有效性。

2 研究区概况

太湖是我国第三大内陆淡水湖泊，整个湖面的面积为2 427.8 km2，横跨江浙两省，相邻较近的地市为无锡、湖州和苏州等城市。本文选取太湖作为研究区域，主要考虑到：太湖水体的叶绿素含量很高并且变化较大，适合于反演模型的建立及验证；另外太湖的污染状况一直受到广泛关注，是一直以来的研究热点，并且积累了许多历史数据可供参考。研究区太湖地理位置及采样点分布见图1。

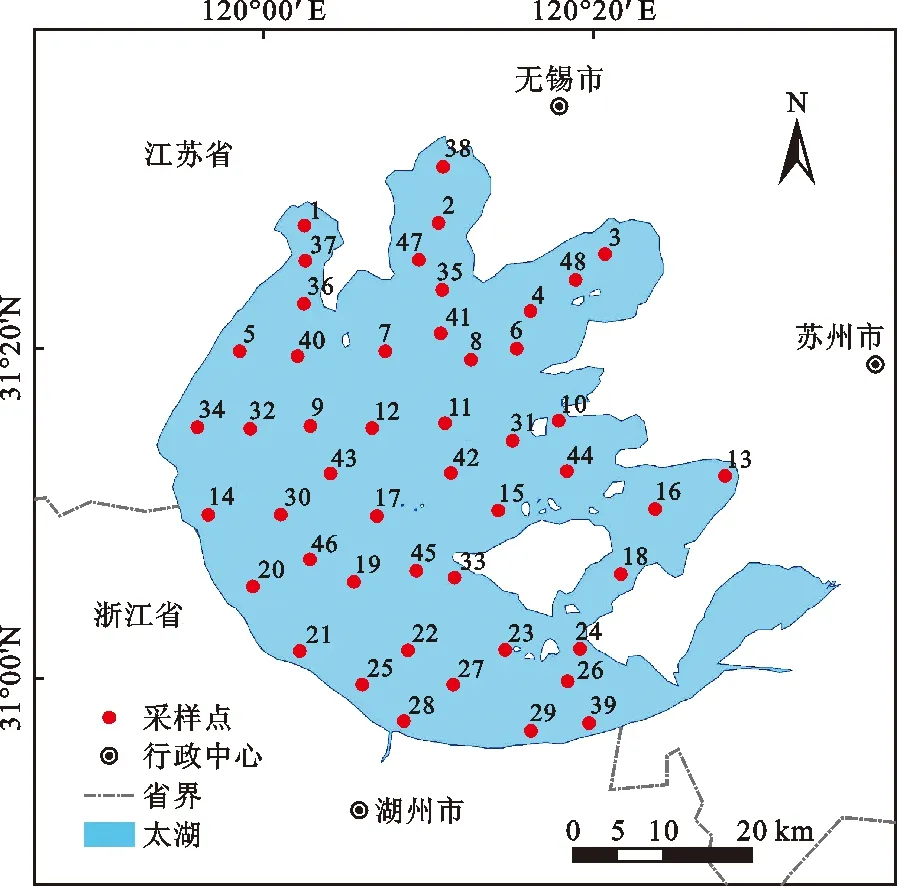
图1 研究区太湖地理位置及采样点分布图

3 数据来源与预处理

3.1 HJ-1A卫星影像介绍

HJ-1A卫星于2008年9月6日发射升空。卫星上搭载的传感器包含可见光和近红外光共4个波段，空间分辨率为30 m，成像宽度为360 km×360 km，可以4 d快速实现地球上同一位置的再次重访。HJ-1A CCD传感器参数及取值如表1所示。

3.2 数据采集

分别于2016年7和10月组织人员对太湖水体进行了2次实地采样，共采集了48个水样样本(采样点分布见图1)，野外测量和记录的参数包括采样点经纬度等信息，实验室采用分光光度法测试和分析样本叶绿素a浓度，各采样点叶绿素a浓度见表2。将48个有效地面采集点数据进行随机抽样，分为训练样本数据和测试样本数据，其中38个数据用于建模，其余10个用于评定模型精度。

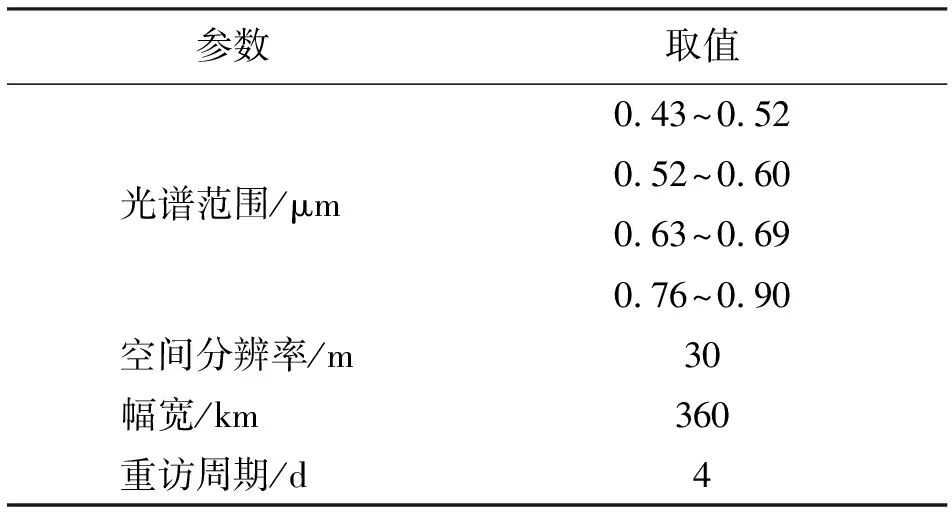
表1 HJ-1A CCD传感器参数及取值

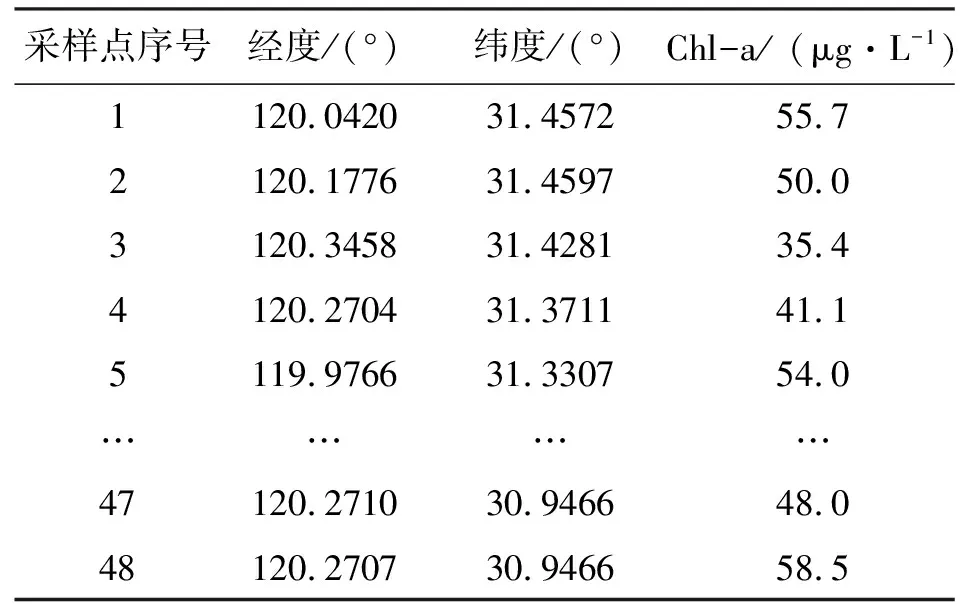
表2 太湖各采样点叶绿素a浓度

3.3 遥感影像预处理

由于本研究直接获取的数据为几何粗校正的HJ-1A CCD影像，因此需要进行必要的数据预处理工作，主要包括几何精校正、辐射定标和大气校正。

3.3.1 几何精校正 在湖面周边均匀选取明显地面控制点，采用二次多项式模型进行几何精校正(校正误差低于1个像元)。以消除或减弱影像成像过程中产生的几何畸变。影像的投影坐标采用UTM投影(通用横轴墨卡托投影)及WGS-84坐标系。

3.3.2 辐射定标 卫星地面接收站获取的是无量纲的HJ-1A CCD影像DN值，然而进行水质参数预测研究中使用的必须是绝对辐射亮度值。影像辐射定标的目的就是将DN值根据定标公式转换为绝对辐射亮度值。

L(λ)=Gain·DN+Bias

(1)

式中：L(λ)为卫星传感器入瞳处的绝对辐射亮度值，W/(m2·sr·μm)；DN为卫星传感器的观测记录值(无量纲)，Gain和Bias分别为定标公式的两个系数，即增益值和偏移值。系数Gain和Bias的定标值如表3所示。

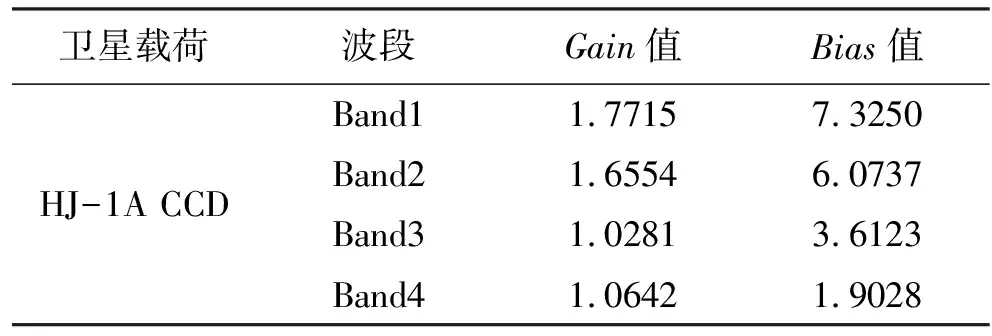
表3 HJ-1A CCD传感器绝对辐射定标系数

3.3.3 大气校正 由于大气分子和气溶胶散射等因素的影响，影像所反映的不是真实的地物信息，因此必须对影像进行大气校正处理[25]。本文利用ENVI5.2的FLAASH模型完成大气校正工作，获取大气校正后真实的反射率图像。

4 ELM模型建立

4.1 ELM 基本原理

假设训练样本由N个不同的随机样本(xi,ti)组成，其中：

xi=[xi1,xi2,…,xin]T(xi∈Rn)

(2)

ti=[ti1,ti2,…,tim]T(ti∈Rm)

(3)

(4)

(j=1,2,…,N)

式中：wi=[wi1,wi2,…,win]T为输入节点与第i个隐层节点之间的权值；βi=[βi1,βi2,…,βim]T为连接第i个隐层节点与输出节点之间的权值；wi·xj为权值wi与样本xj的内积；bi为第i个隐层节点的偏置值。

(5)

存在βi、wi和bi，得到：

(6)

也可以表示为如下矩阵形式：

Hβ=T

(7)

式中：H为网络的隐层输出矩阵，可表示为：

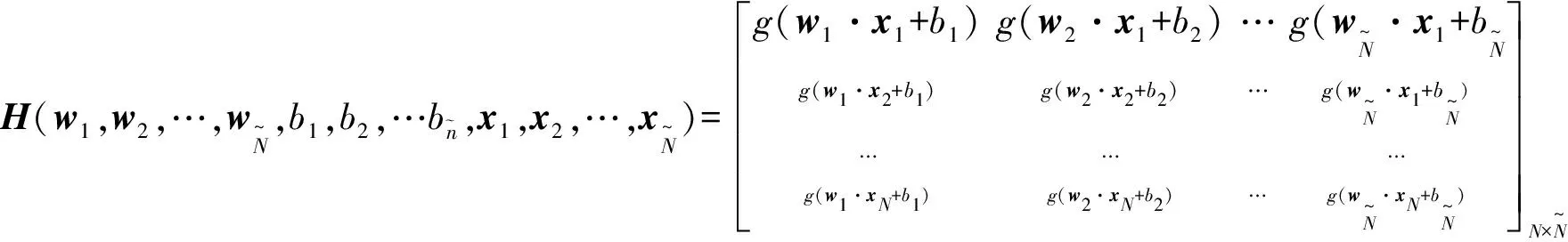
(8)

由于通常情况下，隐层节点数目远远小于训练样本数目，使得公式(6)的模型难以实现，则在该模型中应加上误差E，即：

Hβ=T+E

(9)

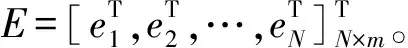
本文定义一个平方损失函数J，其表达式为：

J=∑(βjg(wi,bi,xj)-tj)

(10)

其矩阵形式可以表示为：

J=(Hβ-T)T(Hβ-T)

(11)

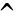
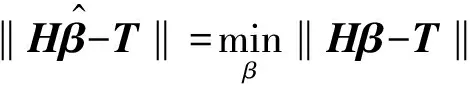
(12)

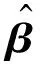
(13)

其中H*=(HTH)-1HT。

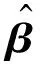
4.2 算法流程

ELM算法通过如下步骤来进行网络权值的维度估计与判定：

(2)模型可以根据步骤(1)随机确定隐层节点参数，即权重值w和隐层节点偏移值b；

(3)计算网络模型隐层输出矩阵H;

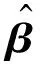
网络输出权重值通过直接求解线性方程组来获得，这正是ELM算法简单、快速和高效的原因。

5 结果与分析

5.1 ELM模型构建与检验

建立用于遥感反演的神经网络模型首先确定反演的影响因素，然后确定网络输入层中神经元的数量。ELM模型中的激励函数主要包括Sigmodial函数、Sine函数、Hardlim函数、Triangular Basis函数和Radial Basis函数。为了更有效地确定模型参数并选择激励函数，本文分别对上述5个函数进行了分析，并将隐含层节点的数量初始化为5，将循环增加至5次，比较分析了不同激励函数和隐层节点数对水体叶绿素a反演的影响程度，其结果如图2所示。

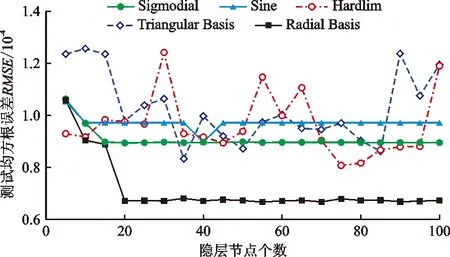
图2 不同激励函数和隐层节点数对水体叶绿素a反演的测试误差

由图2可知，在节点数为20之后，径向基函数(radial basis)开始趋于稳定，在节点数为10之后，Sigmodial函数和Sine函数开始稳定，并且RMSE随着隐层节点数量的增加，Hardlim和triangular basis函数的测试误差波动较大。并且径向基函数在节点数为20之后具有0.7×10-4或更小的测试误差，与其他函数相比误差最小。

本文选择38个采样点的HJ-1A CCD 波段比值B4/B3作为ELM模型的输入层，叶绿素a浓度作为输出层，构建预测模型，利用该构建模型对剩余10个验证样本进行预测，得到预测结果如图3所示。预测值与实测值的拟合程度R2高达0.911 4，均方根误差RMSE仅为1.327 0 μg/L。

5.2 模型对比

为对比验证ELM模型的反演精度，分别利用传统BP神经网络和SVM模型进行叶绿素a浓度反演。BP模型相关参数参考相关文献[26]设置：隐层节点个数为20，学习率设定为0.01，计算步数最大值设定为1 000次，最小均方误差为10-8，网络隐含层激活函数使用“Sigmoid”函数，具体使用“logsig”函数，训练时使用“trainlm”函数；SVM模型通过编写SVMcgForRegress函数来查找模型的最佳参数。选取高斯函数作为其核函数，核函数参数γ和回归惩罚系数均为1，终止判据设置为0.001。

与ELM模型反演过程相似，选择38个采样点HJ-1A CCD 波段比值B4/B3作为模型的输入层，叶绿素a浓度作为输出层，构建预测模型。利用构建的模型分别对剩余10个验证样本进行预测，得到其预测结果如图4、5所示。由图4、5可知，BP模型的预测值与实测值的拟合度R2仅为0.366 3，均方根误差RMSE为3.728 8 μg/L；SVM模型的拟合度略高于BP模型(R2=0.744 8)，均方根误差比BP模型略低(RMSE=2.132 4 μg/L)。总体来看，SVM模型的预测精度略高于传统BP神经网络模型的精度。

对3种模型叶绿素a浓度反演结果的相对误差进行比较，如表4所示。由表4可见，ELM神经网络模型反演精度优于BP和SVM模型，ELM反演结果的最大相对误差为4.60%(序号4)，而BP和SVM神经网络模型的最大相对误差分别为19.04%和8.67%。另外，通过计算表明，ELM模型预测样本的平均相对误差MRE=2.65%，小于SVM和BP模型的平均相对误差(BP和SVM模型的MRE值分别为6.59%和3.89%)。

不难得出如下结论，针对太湖区域叶绿素a浓度反演，ELM模型与BP和SVM模型相比较而言，其整体性能更优。BP神经网络模型结构比ELM模型简单，但预测精度不如ELM模型，BP模型算法的参数需要在运行过程中不断调整。

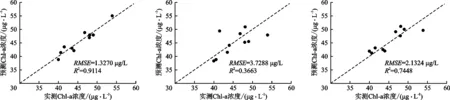
图3 ELM模型的验证结果 图4 BP模型的验证结果 图5 SVM模型的验证结果

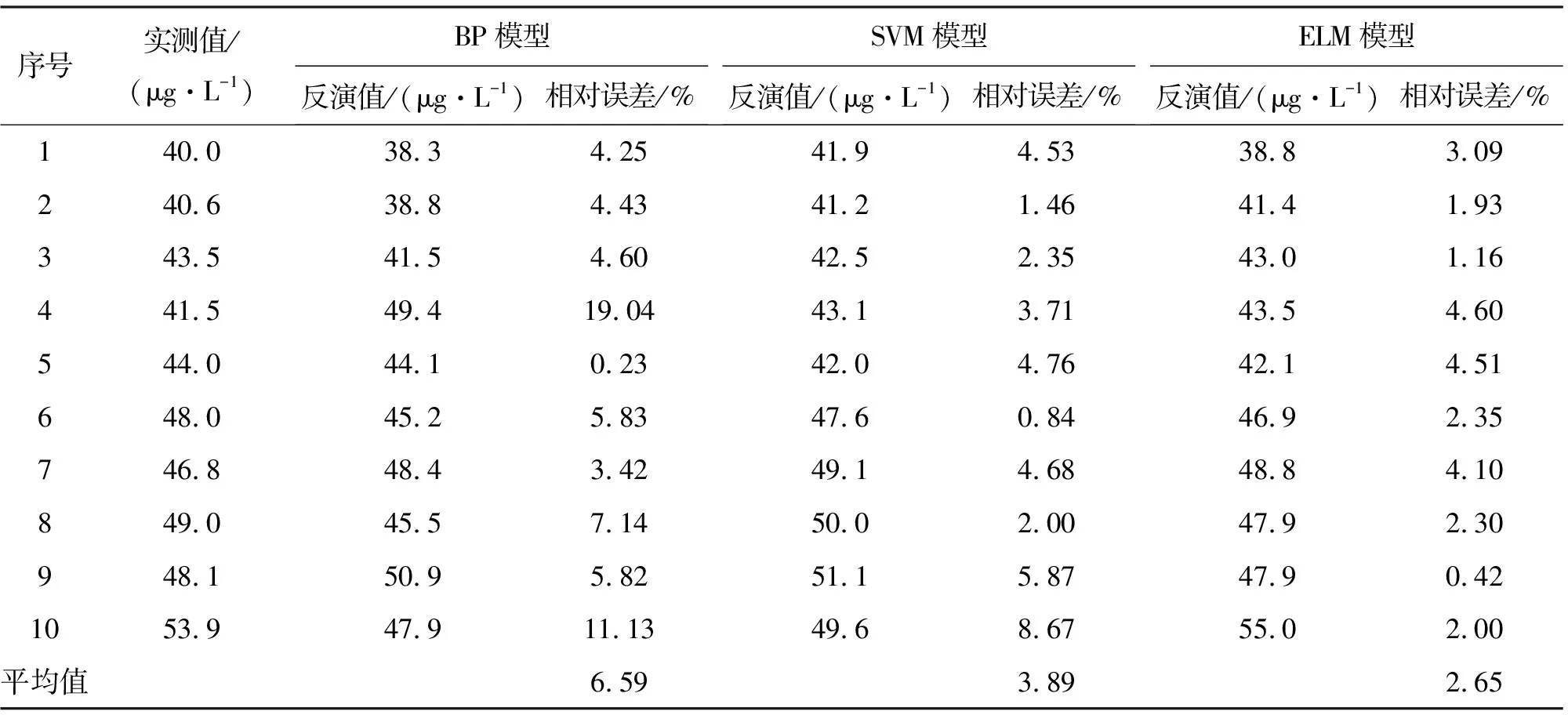
表4 3种模型Chl-a浓度反演结果的相对误差比较

5.3 太湖叶绿素a浓度反演

本文基于ELM模型结合HJ-1A CCD影像反演整个研究区域叶绿素a浓度，反演结果如图6所示。图6中绿色区域为叶绿素高浓度分布区，蓝色区域为叶绿素低浓度分布区。不难发现，从空间分布上看，太湖的叶绿素a浓度分布不均，其总体上呈现从北向南递减的趋势，太湖的中南部湖区(图6中深蓝色区域)是全湖叶绿素浓度最低的区域，连片分布于太湖的中部和离岸较远的南部区域，水面较为开阔。叶绿素a高浓度区域主要集中分布在竺山湖、梅梁湖和贡湖3个区域，浓度高于70 μg/L，最高的区域出现在梅梁湾的西入口、竺山湾西沿岸区、两湾之间以及太湖西部的靠岸边区域，三者的叶绿素a浓度甚至大于100 μg/L。根据湖泊水库监测标准，竺山湖和梅梁湖在叶绿素a浓度这一评价指标上太湖达到Ⅴ类水质的标准。竺山湾和梅梁湾因为受人类活动以及外源性营养盐的输入等因素的影响成为太湖水华最严重的区域。东太湖(图6中灰色部分)的叶绿素a浓度呈现较高的水平，可能是受该区域丰富的沉水植物和挺水植物所致，其反射光谱特征与蓝藻极为相似，并不能准确表征该地区水体的叶绿素a浓度信息，但是反演的结果不能代表水体叶绿素浓度，因此本文根据相关研究对该区域进行了掩膜处理[27]。此外在湖的大部分边缘区域即与陆地交接处，叶绿素a浓度也偏高，这一方面是由于水华易在岸边带堆积，另一方面与岸边带的芦苇分布以及湖边陆地植被干扰有关。

研究结果表明，应用遥感技术可以掌握大范围的水质指标动态变化，随着国内外遥感数据源的增多，遥感技术为太湖叶绿素a浓度进行长时间序列的监测提供了便利。近年来，随着太湖流域环境的不断恶化，更应该加强太湖的水质监测，应用本文提出的遥感反演模型能够大大提高水质监测效率。

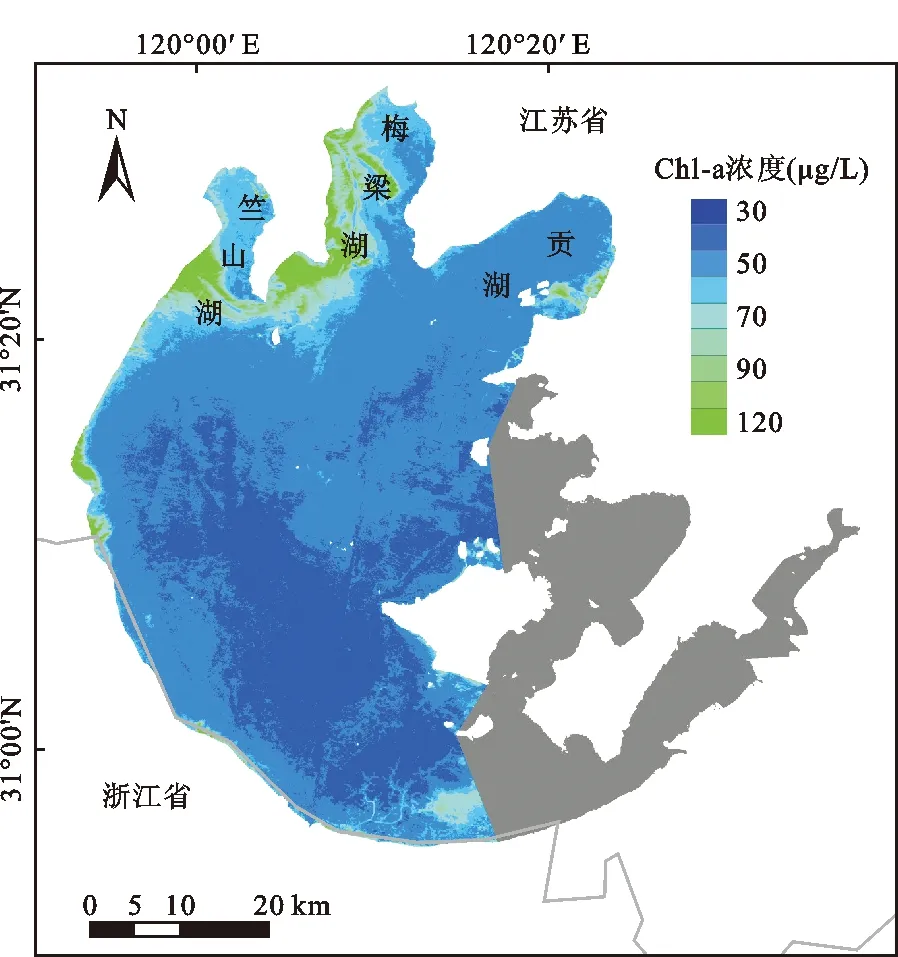
图6 太湖湖面叶绿素a浓度空间分布反演结果

6 结 论

(1)以内陆典型湖泊-太湖为例，基于ELM模型和HJ-1A CCD传感器进行太湖叶绿素a浓度的预测，并交叉对比了BP模型和SVM模型的反演结果。将ELM模型应用于大气校正后的HJ-1A影像上，获取整个太湖湖面叶绿素a浓度的空间分布图。研究结果表明，与传统的BP和SVM模型反演结果相比，ELM具有更高的预测精度。2016年夏季，太湖高浓度叶绿素a主要集中在梅梁湾的西入口、竺山湾西沿岸区、两湾之间以及太湖西部的靠岸边区域。

(2)为ELM模型在内陆湖泊水质遥感监测方面的应用做了尝试性探索研究，说明将ELM模型应用于湖泊水质参数遥感监测是可行的、有效的，后期的研究中再继续获取水体光谱和水质参数等数据，以期继续提高水质参数业务化遥感预测精度。

本文仅研究了太湖区域，为了进一步验证该模型的广泛性，下一步研究应将该模型应用于更加广泛的区域，以期为内陆湖泊水质遥感监测提供便利。