寒区均质土坝混凝土面板冰冻胀破坏的力学分析
夏明海, 秦子鹏, 曾 霞, 马学良, 卢文辉
(1.伊犁哈萨克自治州奎屯河流域水利工程灌溉管理处,新疆 奎屯 833200; 2.中国科学院西北生态环境资源研究院冻土工程国家重点实验室,甘肃 兰州 730000; 3.中国科学院大学,北京 100049;4.新疆玛纳斯河流域管理局,新疆 石河子 832000)
1 研究背景
在中国西北地区,季节性冻土分布广泛。新疆天山以北的大部分地区(以下简称北疆)每年存在5~6个月的季节性冻土[1]。该地区不仅冬季寒冷,且负气温(日最高气温在零度以下)持续时间长(11月中旬至次年3月中上旬,约130 d左右),昼夜温差大,冰盖和冻土与水工建筑物的作用十分剧烈,水利工程的冰冻害问题十分突出。该地区以农业生产为主,由于干旱少雨,农业发展高度依赖人工灌溉。灌溉用水约占当地总用水量的90%左右,灌溉水源多为高山融雪径流,在平原上筑坝蓄水成为解决该地区农业灌溉的一种有效途径。均质土坝由于筑坝材料丰富、结构简单、施工快、造价低和维修方便等优点在各大灌区得到应用和推广。但这些水库平均坝高较低、坝轴线长、蓄水面积大,筑坝土体多为细颗粒土,易在低温天气受到冰冻危害[2-3]。在冬季期,水库被冰盖所覆盖,土坝迎水护坡面板受静冰压力和土体冻胀力的共同作用,遭受冰冻的破坏较为严重[4-6]。
近年来,针对寒区水库的冰冻害问题已开展了大量研究,积累了不少经验[7-14],但目前,仍无明确的理论方法指导冰盖与冻土作用下均质土坝面板的设计。尽管已有学者建立了均质土坝混凝土面板冻胀的有限元模型[15-18],但该方法边界条件复杂,计算过程繁琐,在实践中难以被工程技术人员采用。由于冰盖和冻土的冻胀作用不仅与外界气候、水质等有关,还因受自身结构特征的影响,它们与混凝土面板之间的相互作用过程十分复杂,要精确分析冰盖和冻土共同作用下混凝土面板的冰冻胀破坏问题非常困难。但是通过假设和忽略一些次要因素,提出一种便捷、实用的理论计算方法是可行的。本文在北疆奎屯河流域和玛纳斯河流域开展大量调研的基础上,通过合理假设和对次要问题的简化,依据工程力学和冻土力学的相关理论和方法,分析了在静冰压力和冻土共同作用下均质土坝混凝土面板的冰冻胀破坏问题。该研究可为寒区均质土坝混凝土面板的设计提供一些参考。
2 冰冻胀破坏分析
寒区水库冬季结冰对土坝面板造成破坏的现象非常普遍[19]。冬季库水位波动相对较小,外界升温时,冰盖体积膨胀挤压混凝土面板,致其断裂或发生扰动而造成破坏。冬季坝内的温度场和水分场受外界气候变化的影响。新疆地区冬季雨水稀少,坝内含水率受外界影响较小,坝体下部水分丰富,在土体冻结前水分不断向冻结区域迁移,从而引发坝面板下部一定范围内的土体发生强烈的冻胀作用。在冰推及垫层土体冻胀的共同作用下,土坝混凝土面板的冰冻胀破坏问题突出。
图1为2018年9月在奎屯河流域柳沟水库实地调查研究时拍摄的坝体混凝土面板错位和开裂的情况。该地区冬季气温低,最冷月为1月,平均温度-18℃,最低温度达到-42.3℃。近2008-2018年及2018年冬季日平均气温如图2所示。

注:冬季的水面线和冰盖位置会根据每年入冻前水库来水情况而略有变化

图2 奎屯河流域某气象站点2008-2018年及2018年冬季日平均气温变化
图1(a)为冰盖作用处混凝土面板发生的错位现象,面板上部下沉,下沉深度约5 cm,下部翘起,翘起高度约2 cm。根据2016年现场调查,该水库错位达8 cm以上的面板有41块,共计132 m,其中最大错位为13 cm。在发生错位的面板上很少看到裂缝存在。图1(b)为冰盖作用处混凝土面板发生的开裂现象,裂缝多位于冬季库水位附近,冰盖作用处,裂缝一般贯穿于整块混凝土面板,并大体上平行于水面线,在该水库的其他坝段、左右库岸边坡混凝土面板上类似裂缝分布较多,根据调查,该水库存在贯穿裂缝的面板有44块,共计133 m,缝宽1~2 mm,在发生开裂的面板上很少见到错位现象。上述破坏现象在寒冷地区的其他均质土坝和库岸边坡混凝土面板上也有不同程度的出现[20-28]。
3 均质土坝面板冰冻胀力学分析
3.1 基本约定和假设
(1)坝坡面板为矩形混凝土面板,铺设数量和尺寸均适中,面板之间设有止水缝,在破坏前面板保持良好的整体性。
(2)混凝土材料在受力破坏前变形较小,可将混凝土面板视为刚性材料,冻胀破坏过程为准静态过程,面板在破坏前为平衡状态,发生破坏时为极限平衡状态。
(3)坝体填筑材料均匀、密实,在冻结前已经完成固结,不考虑土的压缩效应。
(4)面板和面板之间视为铰接,铰接点位于面板横截面两端的中心位置。
(5)将坝面冻土的冻胀作用简化为施加在面板上的法向冻胀力和切向冻胀力。
(6)在计算时间段,库水位保持不变,库水面刚好与冰盖底面接触,冰盖底部的水压力为零。
3.2 面板的冰冻胀受力分析
图3为均质土坝上游坝体横断面温湿度分布及面板铺设示意图。图3中坝体护坡由14块矩形混凝土面板构成,面板从上到下的编号为S1、S2、……、S14。C1为坝体内的温度分布曲线。在库水面线以上坝体临空面附近区域,土体温度为负,当深度不断增大,下部土体受外界气候影响小,温度逐渐升高,到达一定深度后,温度增加的幅度很小[20-22]。C2为水的温度分布曲线。水温随着深度增大而逐渐升高,到达一定深度后,水温几乎保持不变[23-25]。C3为坝体内的含水率分布曲线。坝体内的含水率随着高程的降低而不断增大[26-27]。C4为坝体内土体正负温度的分界线,与最大冻结深度有关。

图3 上游坝体横断面温湿度分布及面板铺设示意图
由于水面以下土体不发生冻胀,因此,在进行冰冻胀破坏力学分析时,只需考虑库水位线处及以上的混凝土面板的受力问题。沿坝长取图3库水位线处及以上单位宽度(1 m)的混凝土面板为研究对象。坝面板除了受到自身的重力p作用外,在水面线上方还分别受到静冰压力在法线及切线方向的分力Pi1和Pi2,冻土沿法向、切向的冻胀力q和τ的作用。水面线以下,面板还受到静水压力Pw和土的摩擦力Ff的作用。面板的受力分析如图4所示。

图4 面板冰冻胀破坏受力分析图
3.3 冰冻荷载的计算
3.3.1 冻胀力的计算 由于单块混凝土面板尺寸较小,冻土作用的长度更小,且水位线以上坝体内的含水率变化不大,冻胀量的差别不明显,因此,将法向、切向冻胀力q和τ视为平均冻胀力,沿坝面板均匀分布。冻土法向冻胀力q与其冻胀率η之间存在以下函数关系[28]:
q=E·η
(1)
式中:q为土体的法向冻胀力,kPa;E为冻土的弹性模量,kPa;η为土体的冻胀率,%,可通过实测得到,这里将土体的冻胀率视为平均冻胀率,按照公式(2)计算[29]:
(2)
式中:H为土层冻结深度,mm;Δh为地表冻胀量,mm。
土体的切向冻胀力τ的最大值等于其冻结力,已有的研究表明,当土体温度Ts满足-15℃≤Ts<0℃时,冻结力和负温之间近似为线性关系[30],其表达式如下:
τ=c+b|Ts|
(3)
式中:τ为切向冻胀力,kPa;Ts为冻结土体的温度,℃;c和b均为与土质有关的系数,其中,壤土:c=5,b=1.2;粉质壤土:c=4,b=1;含沙重粉质壤土:c=4,b=6。
3.3.2 冰压力的计算 冬季为非灌溉期,主要用于农业灌溉的水库在整个冰冻期几乎不对下游放水,只从河道引入部分水量以补充渗漏损失,因此,这些水库冬季水位变化缓慢。在冰冻期,宽阔的水库表面会被厚厚的冰雪覆盖,气温升高时,冰盖升温体积膨胀,由于冰盖受到边界条件的限制,进而引起膨胀压力,即静冰压力。静冰压力的大小不仅与冰盖的约束条件(库岸边坡、水工建筑物及冰面形状等)有关,也与气温、冰厚等因素有关。寒冷地区水库的冰盖厚度采用Stefen提出的公式计算[31]:
(4)
式中:δi为冰厚,m;λi为冰的热导率,W/(m·℃),可取2.32 W/(m·℃);Qw为水的结晶潜热,kJ/kg,可取335 kJ/kg;ρi为冰的密度,kg/m3,可取912 kg/m3;I为冻结指数,℃·h。
冻结指数I按下式计算:
I=|T|×t
(5)
式中:T为冬季水位保持不变期间的平均温度,℃;t为库水位固定时间,h。
静冰压力沿冰盖厚度方向的分布是非均匀的[32]。谢永刚[33]根据黑龙江胜利水库的观测数据,给出冰压力沿厚度方向的分布规律,如图5所示。

图5 实测冰压力分布图
由图5可知,冰压力沿冰厚方向呈非对称分布。文献[34]和[35]的观测结果表明,当冰盖厚度为0.8 m左右时,最大冰压力产生在深度为0.25~0.45 m之间,其值可达550 kPa,出现在连续升温时期。由于冰压力的分布会随着冰厚度的变化而变化,而工程技术人员很难在设计之初预测冰盖压力的分布情况,这给冰压力的取值造成困难。《水工建筑物抗冰冻设计规范(GB/T 50662-2011)》[36](以下简称规范)根据冰盖厚度,引入单位长度的平均静冰压力Pi来解决这一问题。规范还给出了水库冰盖厚度与冰压力的关系,如表1所示。

表1 冰厚与冰压力的关系
规范认为,冬季库水面的大小也会对冰压力产生较大影响。因此,规范规定在计算冰压力时,考虑库面大小影响须乘以一定的系数,若库面狭小,则乘以0.87,若库面开阔,则乘以1.25。根据表1,可以结合水库所在地区的冰盖厚度,相应地计算其作用在水工建筑物上的静冰压力值。为了体现冰压力沿厚度方向分布的不均匀性,单位长度上的平均静冰压力qi的作用点位于距冰盖底面冰厚的1/3处,将平均静冰压力pi乘以冰盖的作用长度,就可以计算得到静冰压力Pi。
在计算冰压力对结构的作用时,应先判断冰盖是否会在升温过程中因约束体变形较小,冰盖应力过大而产生破坏。单位宽度冰盖截面上所受平均压应力为:
(6)
式中:σi为单位宽度冰盖截面上所受的平均压应力,kPa;Ai为单位宽度冰盖的横截面面积,m2。

在静冰压力沿面板切向分力Pi1的作用下,冰与混凝土面板的冻结强度也需要进行验算。单位宽度冰盖与混凝土面板冻结处所受的平均切应力为:
(7)
式中:τi为单位宽度冰盖与混凝土面板冻结处所受的平均切应力,kPa。


(8)

静冰压力Pi作用坝面板上,可以分解出一个沿面板法线方向的分力Pi1和一个沿面板切线方向的分力Pi2(见图4)。
冰压力沿着面板法线、切线方向的分力Pi1和Pi2的大小为:
Pi1=Pisinα
(9)
Pi2=Picosα
(10)
式中:Pi1、Pi2分别为静冰压力沿面板法线和切线方向的分力,kN;Pi为静冰压力,kN;α为坝面与水平面的夹角,(°)。
3.4 面板的内力计算
由于在水面线以上的冻胀力自上而下逐渐增大,而且第3块板上还受到静冰压力的作用,因此,第1和第2块板及它们之间的填缝相对安全,而第3块板及其与第2块板间的填缝承受的弯矩和剪力较大,相对容易遭受冰冻破坏,所以主要对第3块板进行力学分析。根据对上述荷载的分析结果,进行第3块板的受力分析,如图6所示。

图6 第3块面板受力分析图
根据图6,沿x方向列力的平衡方程,计算第3块混凝土面板与第2块板的作用力FNC如下:
FNC=Pi2+nLτ-pLsinα-Ff
(11)
式中:FNC为第3板与第2块板之间的作用力,kN;n为水面线以上面板斜向长度占总长度的比例;L为面板的斜向长度,m;τ为冻土的切向冻胀力,kPa;p为面板单位长度所受到的重力,kN/m;Ff对坝面板与未冻土之间的静摩擦力,kN。
对图6中的D点列力矩平衡方程,计算混凝土面板在C截面沿y方向上的支座反力FCY得

(12)
式中:FCy为混凝土面板在C截面沿y方向上的支座反力,kN;m为静冰压力作用点以上面板斜向长度占总长度的比例;h为面板的厚度,m;Pw为静水压力的合力,kN;q为土体的法向冻胀力,kPa。
沿y方向列力的平衡方程,计算混凝土面板在D截面沿y方向上的支座反力FDy得:
(13)
式中:FDy为混凝土面板在D截面沿y方向上的支座反力,kN。
采用截面法,计算0≤x FN(x)=(psinα-τ)x+FNC (14) FQ(x)=qx+FCy (15) (16) 计算mL≤x FN(x)=(psinα-τ)x+FNC-Pi2 (17) FQ(x)=qx+FCy-Pi1 (18) (19) 计算nL≤x (20) (21) (22) 由于冻土的切向冻胀力对混凝土面板的弯矩影响较小,在上述弯矩计算过程中将其进行了忽略。采用上述公式可以计算混凝土面板任意位置的内力。 均质土坝混凝土面板的内力分布和危险截面的位置会随冻胀力和静冰压力的变化而发生改变。冻胀力的数值与气温和筑坝材料有关,冰压力受气温、冰厚、边界条件等因素的影响,因此筑坝材料、地区气温不同,则面板的冻胀破坏程度也会存在较大差异。根据野外观测,北疆地区的大中型水库在2018年和2019年1月份的冰厚在0.38~0.45 m之间,静冰压力Pi在110 kN/m左右,当静冰压力保持不变时,轴力不变(忽略切向冻胀力的影响),土体的法向冻胀力的变化与弯矩和剪力之间的关系,如图7所示(MI、MJ表示I、J截面处的弯矩,SC、SI、SJ、SD分别表示C、I、J、D截面处的剪力)。 图7 法向冻胀力与弯矩和剪力之间的关系 当法向冻胀力q较小时,I截面的处的弯矩和剪力最大,此时,绘制第3块混凝土面板的内力图(轴力以面板受拉为正,受压为负;剪力以面板顺时针转动为正,逆时针转动为负;弯矩图以面板下部受拉,上部受压为正,以面板上部受拉,下部受压为负,弯矩图绘制在受拉一侧),如图8所示。 由图8可知,在C截面处存在最大的轴力,该轴力为压力。该截面处剪力较大,弯矩为零。由于混凝土的抗压和抗剪强度较高,该处不会发生受压和受剪破坏,但在C截面接缝处的填充材料可能发生剪切破坏。在I截面处轴力(压力)有所减小,剪力和弯矩达到最大,该截面由于受到较大的弯矩作用,混凝土的抗拉强度较小,面板下部可能会发生受拉破坏。在J截面处的轴力为拉力,且拉力值相对较大,在该截面处剪力接近于零,弯矩相对较小,在拉力和弯矩共同作用下,该截面混凝土面板下部也有可能发生受拉破坏。因此,需要对C端接缝填充物进行抗剪强度验算,对I截面处进行弯压强度验算,对J截面进行弯拉强度验算。 注:FN max、FQ max和Mmax分别为轴力、剪力和弯矩绝对值的最大值。I为冰压力的作用点;J为冰盖的下边缘库水面线位置 当法向冻胀力q不断增大,大于50 kPa后,轴力不变,最大剪力和最大弯矩的位置发生了变化,此时,绘制第3块混凝土面板的内力分布简图,如图9所示。 注:FQ max和Mmax分别为剪力和弯矩绝对值的最大值。I为冰压力的作用点;J为冰盖的下边缘库水面线位置 由图9可知,在C截面处剪力达到最大,弯矩为零,C截面接缝处的填充材料可能会发生剪切破坏。在J截面处的轴力为拉力,剪力有所减小,弯矩达到最大(混凝土面板上部受拉,下部受压)。在拉力和弯矩的共同作用下,该处混凝土面板上部有可能被拉断。因此,需要对C端接缝填充物进行抗剪强度验算,对J截面进行弯拉强度验算。 当法向冻胀力不变时,改变静冰压力的大小,同样可以改变最大内力的位置,因此,在冻土与静冰压力共同作用下,混凝土面板可能在I截面处先发生破坏,也可能在J截面处先发生破坏,这取决于两个荷载值的相对大小。 面板是否发生冰冻胀破坏,一般从两方面判断,一方面是判断接缝处所受的剪力值是否达到或超过填充材料的抗剪强度值,另一方面是判断在弯矩和拉力的作用下混凝土面板是否发生强度破坏。 (1)面板接缝填充材料破坏的判断准则。混凝土面板接缝处的剪力值采用公式(23)计算: (23) 式中:τf为混凝土面板接缝处的剪切应力,kPa;Af为混凝土面板接缝处的剪切面积,m2。FQf为混凝土面板接缝处的剪力,kN,当忽略接缝的宽度时,其值等于接缝处混凝土面板的剪力值。 (2)混凝土冻胀强度破坏的判断准则。在轴力和弯矩共同作用下坝面板上的最大拉应力计算公式如下: (24) 式中:σmax为在冻胀力及其他荷载作用下冰盖作用处混凝土面板上产生的最大应力,kPa;Ac为单位宽度混凝土面板的横截面面积,m2;W为混凝土面板在单位宽度上的抗弯截面系数,m3。 将公式(24)计算出的最大应力σmax与面板混凝土的抗拉强度值ft进行比较,即可判断混凝土面板的抗冻拔强度是否满足要求。当σmax (1)计算冻胀力。土体冻结深度H=1.5 m,冻土的弹性模量E=2 000 kPa,冻胀量Δh=42 mm,根据式(1)和式(2)计算法向冻胀力q=57.61 kPa。土体为粉质壤土,土体温度为-10℃,根据式(3)计算得冻土切向冻胀力τ=14 kPa。 (3)计算危险截面上的内力。混凝土面板长L=3 m,单位宽度混凝土面板的重量p=0.48 kN/m,坡角α=26.57°,静水压力的合力Pw=7.10 kN。未冻土与混凝土面板的摩擦系数为0.37,静冰压力作用点以上面板斜向长度占总长度的比例m=0.195 4,水面线以上面板斜向长度占总长度的比例n=0.4。根据公式(11)、(12)和(13)计算得第3块混凝土面板与第2块板的作用力FNC=90.87 kN,支座反力FCy=-10.06 kN,支座反力FDy=-1.67 kN。 根据3.5节的分析,需要验算C截面接缝处填充材料的剪切强度,J截面混凝土面板上部边缘处的弯拉强度。 根据公式(15)计算得FQC=10.06 kN,混凝土面板接缝的宽度较小,可以忽略不计,接缝处填充材料所受剪力FQf=FQC=10.06 kN。根据公式(20)计算得FNJ=26.30 kN。根据公式(22)计算得MJ=11.52 kN·m(面板下部受拉,上部受压)。 (5)验算冻混凝土面板的抗冻胀强度。单位宽度混凝土面板的横截面面积Ac=0.2 m2,抗弯截面系数W=0.0067 m3,根据公式(24)计算J截面混凝土面板上部边缘处的拉应力σJ=1 851.50 kPa。由于混凝土的轴心抗拉强度值ft=1 780 kPa,而J截面混凝土面板上部边缘处的拉应力σJ=1 851.50 kPa>ft=1 780 kPa,该处混凝土面板因上部受力拉而发生破坏。因此,在静冰压力和冻土共同作用下,在库水面线附近的混凝土面板上部边缘会因受到的拉应力过大而发生开裂,这就是为什么我们在寒区平原水库坝面上看到的裂缝都分布在冬季冰盖或水面线附近,且这些裂缝都是贯穿性的,并平行于库水面线。 由以上计算分析可知,在冰压力和冻土共同作用下,混凝土面板会发生错位或开裂,但是这两种破坏一般不会同时发生,因为当面板发生错位运动时,会消减冰压力的破坏作用,而冰压力的作用实际上是随温度变化而循环往复进行,当温度降低,冰盖收缩时,面板就可以恢复原位,这也是很少在能够发生错位的面板上看到裂缝的原因(如图1(a)所示面板)。而有些面板在约束力的作用下很难发生错位运动,在冰压力和冻土共同作用下,很容易发生如图1(b)所示面板那样的断裂破坏。 (1)本文针对寒区水库结冰后,冰盖和土体共同作用下,均质土坝混凝土面板的冰冻胀破坏问题开展研究,提出了混凝土面板的冻胀力学模型及冻胀破坏的判断准则,计算参数少,使复杂的冰冻胀问题简单化。 (2)根据力学分析,水面线附近弯矩最大,混凝土面板上部受拉下部受压,由于混凝土的抗压强度远大于其抗拉强度,容易在该处发生强度破坏,这些裂缝往往都是贯穿性的,并平行于库水面线。 (3)由于混凝土的抗剪强度远大于面板接缝填充物的抗剪强度,而在冰盖作用处上部接缝处受到的剪力最大,该处的填充材料往往会发生剪切强度破坏。填充材料发生破坏后,在冰压力和冻土共同作用下,混凝土面板容易发生错位。面板的错位可以消减部分静冰压力,在发生错位的面板上很少发现冻胀裂缝的存在。 (4)由于在计算过程中,使用了一些假设,并忽略了很多难以量化的影响因素,仅考虑宏观上对面板冰冻胀影响的几个主要因素,使计算公式简便实用。计算过程中所采用参数可以根据具体工程需要开展进一步的室内外试验得到。
3.5 面板内力分布的讨论



3.6 冻胀破坏的判断准则

4 工程算例


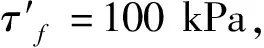
5 结 论

