细纤维对于传统滤料过滤效率的优化研究

韩少龙

(中国电力工程有限公司，北京100048)

近年来，空气质量问题日益加重。随着工业的粗犷式发展，空气中PM2.5含量逐渐升高，严重威胁着人体健康，导致诸如：肺癌、哮喘以及心脑血管疾病的发病率逐年升高[1-2]。为了减少空气中PM2.5含量，除了要弄清主要排放源之外，还需要大力开发优化现有过滤装置。其中，纤维滤料因其对于颗粒物有很好的过滤效果，备受关注[3-5]。可是，传统纤维滤料主要依靠碰撞和拦截两种机制过滤颗粒物。这些过滤机理对于粒径大于1μm的颗粒物能够起到很好的过滤效果，但是对于小于1μm的颗粒物其过滤效果较差[6-8]。对于小于1μm的颗粒物来说，其过滤过程主要受到布朗扩散的影响，因而传统结构的纤维滤料难以将其从空气中有效清除。为了提高颗粒物的过滤效果，近年来一些学者研究了异形纤维的过滤过程，如正方形纤维、三角形纤维、椭圆形纤维等异形纤维对于细小颗粒物的过滤效率[9-11]，李威[12]采用数值方法研究了多层不同尺寸纤维掺混方式对于颗粒物的过滤效率。为了提高传统纤维对于颗粒物的过滤效果，本研究采用数值手段探究不同形式的纤维排布方式对于颗粒物的过滤效果，进一步优化现有纤维的布置形式。

1 数值模拟

1.1 数值模型

纤维滤料的内部流动属于斯托克斯流动，其中，惯性作用可以忽略不计，控制方程如下所示：

式中：p——压力，Pa；u——x 方向速度，m/s；v——y 方向速度，m/s；x——x坐标；y——y坐标；μ——动力粘性系数，N·s/m2。

本研究使用商业CFD(Computational Fluid Dynamics)软件FLUENT求解上述方程[13]。此外，真实的纤维滤料内部纤维呈现随机分布状态。为了得到这种随机状态的纤维分布形式，本研究使用MATLAB程序中的随机算法生成纤维圆心坐标，随后对该坐标进行移动，得到圆弧上的两点。最终，这三点坐标在网格划分软件Gambit中即可生成一个圆形纤维。将这些随机分布的纤维坐标通过Script文件导入Gambit中生成整个纤维滤料的几何模型，如图1所示：

图1 几何模型与边界条件

由图1可知，模型进口为速度进口边界，出口采用压力出口，上下两个表面为对称边界条件。由于真实滤料尺寸较大，将整个滤料计入求解区域，对于现有计算资源难以承受。Hosseini等[14]的研究显示：随机选取滤料内纤维直径df(纤维直径)40df×40df的面积，可以保证求解结果与实际情况相符，因而本研究采用该种方法。同时，由于纤维呈现随机状态分布，四边形网格无法有效划分计算区域，因而采用三角形网格划分计算区域。与文献[14]相似，每个纤维采用60个网格进行划分。

1.2 颗粒运动模型

对于粒径小于500 nm的颗粒来讲，其运动过程主要受到布朗运动的影响。且颗粒相可以当作连续相来处理。因而，采用欧拉方法求解颗粒物浓度变化：

式中：C——无量纲的颗粒物浓度；D——颗粒扩散系数；u——x方向速度，m/s；v——y方向速度，m/s。在模型的进口处，C=1；对于颗粒物表面，C=0。

对于粒径大于等于500 nm的颗粒，主要受到惯性和拦截作用的影响。此时，欧拉方法不适用。因而，采用拉格朗日方法追踪颗粒的运动轨迹。其控制方程如下：

式中：n(t)——布朗力 ，N；Gi——随机数(均值为零，方差为1的高斯随机函数)；up——颗粒速度，m/s；dp——颗粒直径，μm；Cc——格林汉姆修正系数(-)；u——速度矢量 ，m/s；up——颗粒物速度矢量，m/s；ρp——颗粒物密度，kg/m3；μ——动力粘性系数，N·s/m2；Δt——颗粒的时间步长，s；S0——光谱强度函数。

其中，时间步长设为1×10-6s。为了实现纤维对于颗粒的拦截作用，采用UDF(User Defined Function)编写子程序监视颗粒物中心与纤维表面的相对位置，当距离小于df/2时，将颗粒物从计算域中清除。同时，使用UDF编写随机运动程序，实现颗粒物的布朗运动特征。

1.3 模型验证

为了方便预测纤维滤料的过滤效果，一些学者根据大量实验和模拟结果提出了较多的经验公式。为了验证本研究使用的2D模型，特采用Stechkina and Fuchs以及Lee and Liu

提出的经验公式[15]进行验证。图2显示了纤维直径(df)=5 μm，进口速度(U)=0.05 m/s和固体体积百分数(SVF)=10%的情况下，模拟与经验公式预测值的比较结果。图2中右侧为单位距离滤料下的颗粒渗透率(ln(p)/t)。可以看到在颗粒直径(dp)=50nm时，模拟结果的差别较大，达到15.3%。在其他粒径下，实验结果与模拟结果的对应效果较好。

图2 模拟结果与经验公式比较

为了进一步展示2D模型的效果，图3和图4分别给出了两种典型工况下，欧拉和拉格朗日方法的计算结果。可以看出在使用欧拉方法时，靠近纤维的部分颗粒浓度出现明显降低；使用拉格朗日方法时，可以观察到颗粒与纤维的碰撞以及拦截过程。

图3 欧拉方法

图4 拉格朗日方法

2 工况介绍

本研究的主要目的在于优化传统滤料中纤维的布置方式，探究优化后的纤维布置方式对于颗粒物的过滤效果。本研究中以df=10μm的纤维为研究对象，其中SVF=5%。为了优化其内部结构，使用df=5μm的纤维与其进行掺混。需要注意的是，5μm纤维的滤料的SVF同样采用5%。同时，两种细纤维与粗纤维的面积比分别为：10%和20%，两种进口风速：U=0.1 m/s和U=0.5 m/s。文中对3种掺混方式进行研究，分别为后面布置、前面布置和混合布置方式，即将细纤维(df=5μm)分别布置于粗纤维的后面、前面和内部。本研究中对粒径小于2.5μm的物种颗粒进行研究，选取的颗粒粒径分别为：100 nm、250 nm、500 nm、1 000 nm和1 500 nm。

图5 细纤维布置于粗纤维后面

3 结果与讨论

图8、图9给出了在10%的配比下，不同进口风速时，3种布置方式与未加入细纤维情况的对比结果。如图8所示，在低风速的条件下(U=0.1 m/s)，优化后的纤维结构在一些情况下确实可以提高传统纤维的过滤效果。此外，后面布置的情况与其他两种优化方式相比，其过滤效果更好，颗粒的渗透率更低。对于粒径较小的颗粒(dp≤500 nm)，前面布置和后面布置的方式都能够降低颗粒的渗透率。然而，对于较大的粒径(dp＞500 nm)，后面布置的形式也无法明显地降低颗粒物的渗透率。

图6 细纤维布置于粗纤维前面

图7 细纤维、粗纤维混合布置

图9给出了大风速情况下的比较结果。可以看出，对于粒径小于等于500 nm的颗粒来说，3种布置方式都没能有效地降低颗粒物的渗透率。然而，对于粒径为1 000 nm和1 500 nm的颗粒来讲，后面布置和混合布置降低了颗粒的渗透率，尤其对于1 500 nm的颗粒，颗粒物渗透率出现了明显的降低。这种状况与颗粒物的惯性作用有关，对于粒径为1 500 nm的颗粒来讲，在大风速下其斯托克斯数(Stk)达到0.8左右，颗粒与纤维的碰撞明显增大，因而其渗透率降低。

图8 配比为10%，U=0.1 m/s时3种布置方式的颗粒渗透率对比

图9 配比为10%，U=0.5 m/s时3种布置方式的颗粒渗透率对比

图10、图11给出了20%的配比下，3种布置方式的过滤效果。对于低风速的情况(U=0.1 m/s)，3种布置方式的过滤效率较为接近，并且相应的都低于未添加细纤维的情况。尤其对于dp=100 nm和dp=1 500 nm的颗粒，使渗透率出现了明显的降低。并且在20%的配比下，由于细纤维比例的增大，3种布置方式的过滤效果十分相近，不过后面布置的形式表现更好。这说明，配比比例的增大降低了不同布置方式的差异，在以后的优化研究中是一个需要重点考虑的参数。

图10 配比为20%，U=0.1m/s时3种布置方式颗粒渗透率对比

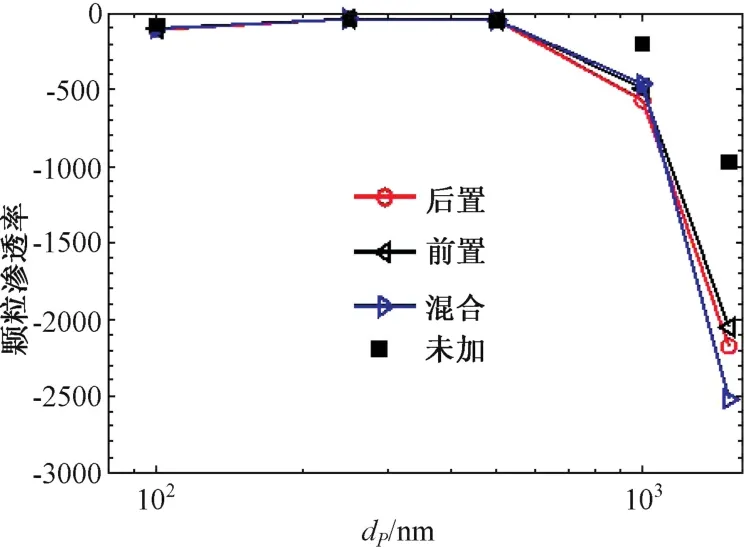
图11 配比为20%，U=0.5m/s时3种布置方式颗粒渗透率对比

图10给出了大风速的情况下过滤效率的对比结果。与10%的配比情况相似，对于粒径小于等于500 nm的颗粒来讲，3种布置方式并不能降低颗粒的渗透率。而对于粒径大于500 nm的颗粒，3种布置方式都明显地降低了颗粒的渗透。不过，需要注意的是，与10%配比的情况不同，此时前面布置的形式也很好地降低了颗粒的渗透。再一次说明，高配比下不同布置方式引起的过滤效率差异逐渐降低。

图12～图14比较了不同配比下各种布置方式的颗粒渗透率。可以看出，20%的配比对应着较低的颗粒物渗透率。相比于10%的配比，20%的配比增大了细纤维(df=5 μm)掺混数量更多的比例，有效碰撞面积增加，从而增大了颗粒物与纤维的碰撞几率。同时也要看到，对于小于500 nm的小颗粒，其运动主要受到布朗运动的影响，增大有效碰撞面积后确实对其渗透率的降低起到了相应作用，但是相比于粒径较大的颗粒，这种降低效果不明显。

图12 后面布置方式不同配比下颗粒物的渗透率对比

图13 前面布置方式不同配比下颗粒物的渗透率对比

图14 混合布置方式不同配比下颗粒的渗透率对比

综上可知，在粗纤维滤料中掺混细纤维可以有效地降低颗粒物的渗透效率。尤其是细纤维后面布置的方式，对于降低颗粒的渗透率有着很好的效果。此外，增加细纤维的配比会增大有效碰撞面积，从而降低颗粒物的渗透率。并且，在较高配比下，细纤维不同的布置方式导致的过滤效率差异会降低。因此，在传统纤维后面布置尺寸较小的细纤维可以很好地提高其过滤效率。在以后的工作中还需要进一步研究细纤维的掺混比例等参数。