基于振幅差分的Φ-OTDR光纤振动信号检测方法
李 新, 韩家广,2, 熊显名, 胡放荣, 陈柳江
(1.桂林电子科技大学 电子工程与自动化学院,广西 桂林 541004; 2.天津大学 精密仪器与光电子工程学院,天津 300072)
相敏光时域反射仪(phase-sensitive optical time domain reflectometer,简称Φ-OTDR)具有全分布式传感器的能力,可以对长距离传感光纤上的物理量实现连续测量,因此该分布式光纤传感技术在国内外备受关注[1-2]。分布式光纤传感器自身有很多优点,如远程操作能力和电磁噪声抗干扰能力,尺寸小,通用性好,成本相对低[3]。这种传感器可实现光纤上任何一点的不同物理参数(应变、温度、振动、压力等)的检测,并且每个监测点的成本相对较低。因此,基于Φ-OTDR的分布式传感器应用广泛,包括井下地震波的异常振动检测、石油管道安全监测、水下声波通信以及火车、汽车定位[4]。
1993年Taylor等[5]首次提出了相位敏感型光时域反射仪,该传感系统所使用的光源通常来源于kHz级别的窄线宽激光器,其原理是当外部受到扰动时,引起传感光纤中后向瑞利散射(RBS)信号干涉加强,通过信号光功率波动实现外部扰动监测。2014年,叶青等[6]利用瀑布图实现了车辆的定位和识别,通过检测车辆的外部扰动信号跟踪车辆的位置和提取车辆速度等信息,从瀑布图中可以非常清晰地看到车辆行驶的信号,检测效果良好。Φ-OTDR技术利用瀑布图作为车辆监测方法在实验中并不经常使用,比较常见的是使用幅度差分的方法[7],通过在Φ-OTDR系统中采集多条原始的瑞利散射曲线,从第一条信号曲线的幅值减去相邻周期信号曲线的幅值,计算多条差值曲线的绝对幅值并累加,最后通过峰值检测实现干扰事件的定位。但是该幅度差分算法对频率具有选择性,对于某些频段的信号无法检测,对低频缓变信号检测效果也欠佳。为此,提出一种基于振幅差分的光纤振动信号检测方法。
1 Φ-OTDR系统
1.1 Φ-OTDR的传感原理
瑞利散射点模型示意图如图1所示。将光脉冲从光纤的一端注入到传感光纤中,当光脉冲遇到光纤中分布不均匀的散射点时会发生瑞利散射,该散射主要来源于纤芯折射率的微观折射率波动,从尺寸上来看,这些折射率波动的大小远远小于入射光的波长[8]。注入的光脉冲在光纤中向前继续传播时,脉冲光将持续遇到大量散射点并不断产生瑞利散射信号,这些散射信号能够沿光纤反向传输。若光纤传感器上某位置存在干扰事件,则该干扰位置的光纤折射率会发生变化。由于弹光效应,导致该处散射光的相位、偏振态或散射点之间的光程差也会发生变化。

图1 瑞利散射点模型示意图
设注入传感光纤的探测光脉冲宽度为W,若光纤长度L足够长,则任意时刻t反射到光电探测器的瑞利散射信号的电场强度[8-9]可表示为
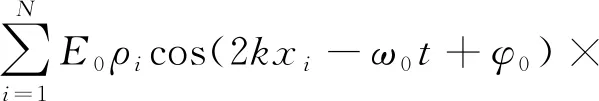
(1)
其中:E0为注入脉冲的电场强度;ρi为散射系数;k为脉冲光在光纤中的波数,k=2πnxi/λ;xi为第i个散射点的位置;ω0为注入脉冲光的角频率;φ0为探测光的初始相位;rect(x)为矩形函数,

(2)
由式(1)、(2)可知,Φ-OTDR后向瑞利散射信号都是由半个脉冲长度内光纤散射点产生的后向瑞利散射信号互相干涉叠加而形成的散射点。因此,当光脉冲沿着光纤完成一次传播时,即产生了一次连续的散射点。由于散射点位置的随机性,引起光纤不同位置后向瑞利散射光的干涉强度产生随机波动,最后通过不断对比散射光波形的变化来定位扰动事件的位置。在单模传感光纤上某处放一个压电陶瓷,并施加频率为100 Hz振动信号,利用上位机采集400条原始的后向瑞利散射光信号曲线并叠加,如图2所示。从图2可看出,约50 m处的信号光幅度波动起伏相对较大,初步可定位扰动事件的位置在50 m附近。

图2 400条后向瑞利散射光信号曲线叠加
反射传播的后向瑞利散射光经光电探测器转换的光电流[10]为
(3)
将式(3)展开,忽略2倍光频项(忽略损耗),可得
(4)
其中2k(xi-xj)=φi-φj。若第q(q∈[1,N])个散射中心引入扰动,相应相位扰动引入一个相移φp,则非扰动和扰动信号之间的相应电流强度变化为

cos(φi-φj-φp)]。
(5)
由式(5)可知,在施加振动的情况下,Φ-OTDR系统主要表现为非扰动和扰动信号相位差的变化,同时也可以得出后向瑞利散射光信号强度与输入光脉冲强度成正比。较高的平均后向散射强度会产生较大的信号变化,从而提高系统的灵敏度,降低传感信号的衰落。为了得到更强的后向瑞利散射光信号,可以提高光脉冲的功率,但会增大光纤非线性效应。从式(5)也可知,任何一个散射点受到干扰都会引起输出电流信号发生强烈的变化,因此,Φ-OTDR传感系统可识别探测微弱的干扰事件。
1.2 Φ-OTDR系统结构
图3为相干探测型Φ-OTDR系统结构。线宽小于3 kHz的窄线宽激光器发射的连续光被90∶10光耦合器分成2束连续光,其中90%的连续光作为探测光,10%作为本振光。探测光经过声光调制器(AOM)调制生成脉冲光,此时脉冲光被频移200 MHz,经过环形器注入到单模传感光纤中。从光纤返回的后向瑞利散射信号光与本振光通过50∶50的耦合器进行拍频,得到200 MHz的拍频信号,拍频信号包含了信号光的幅度、频率和相位等全部信息。拍频信号经过200 MHz的平衡探测器(BPD)转换成电信号,再经过放大和滤波模块被解调板解调,解调完成的信号由高速示波器采集,并由软件程序处理。

图3 Φ-OTDR系统结构
2 Φ-OTDR的性能指标
2.1 频率响应能力
频率响应是衡量Φ-OTDR系统可以感知信号最大频率的能力,主要由脉冲光的采样频率决定。根据奈奎斯特定律,Φ-OTDR系统可以感知信号的最大频率为
(6)
采样周期受到最大传感距离的限制,光脉冲注入光纤的传感距离为
(7)
其中:c为真空中的光速;n为光纤中纤芯的折射率。结合式(6)、(7)得,
(8)
由式(8)可知,传感距离越长,探测到的信号频率就越低,这对于特定的振动事件,如深海探测、人工挖掘等,所探测的信号频率远远不够。为此,很多研究人员提出了各种改进方法来提高Φ-OTDR的最大频率响应,为各种检测领域提供了技术基础。另外,Φ-OTDR系统最小的探测频率一般取决于系统的频率分辨率。
2.2 动态响应范围
动态响应范围是Φ-OTDR系统十分重要的一个性能参数,它直接影响Φ-OTDR系统可探测的传感光纤的最大长度,该值越大,可探测的光纤长度越长。动态响应范围[13]为
(9)
其中:PS0为光纤起始端后向瑞利散射光峰值功率;PN为系统噪声峰值功率。由式(9)可知,可通过提高光纤起始端后向瑞利散射光功率来提高Φ-OTDR系统的动态响应范围,但功率超过一定的极限也会引起光纤非线性效应,严重影响系统性能,反而增大系统背景噪声。
2.3 空间分辨率
空间分辨率是分辨两次干扰事件的最小距离,用来衡量Φ-OTDR系统干扰事件定位精度的度量。Φ-OTDR系统空间分辨率为
(10)
其中:v为脉冲光在光纤中的传播速度;W为脉冲光的宽度。由式(10)可知,可通过降低脉冲光的宽度来提高空间分辨率,但脉冲光宽度太小会影响后向瑞利散射信号光的功率,导致系统信噪比降低,因此两者需要权衡。
2.4 信噪比
信噪比[14]影响Φ-OTDR系统的传感质量,其定义为后向瑞利散射光功率PS与系统噪声功率PN之比,
(11)
对于Φ-OTDR系统,光脉冲在传感光纤传输过程中光功率会有所损耗,导致传感光纤上产生的后向瑞利散射光的功率也相对减小,因此信噪比会随着光纤长度增长而减小。为提高系统的信噪比,可采用的方法为改善Φ-OTDR系统光路、提高硬件部分的灵敏度、改善软件部分的信号处理。对于系统灵敏度而言,激光光源的线宽越窄,后向瑞利散射信号的相干效应越强,系统的灵敏度就越高。当Φ-OTDR系统灵敏度越高,系统对微弱干扰事件的响应能力就越强,得到的系统信噪比也会更高。
3 信号处理与实验仿真
3.1 振幅差分法
在分布式光纤Φ-OTDR系统的应用中,振动信号处理一般采用移动平均和移动差分算法[11]、时频域算法、振幅差分法[12]、机器学习算法等,其中振幅差分法是最常见也是最方便快捷的一种方法。振幅差分法的基本原理是:假设光纤足够长,每次脉冲光注入传感光纤产生一帧后向瑞利散射信号光,若一定时间内将N个脉冲光注入传感光纤,并由数据采集卡采集,则采集的后向瑞利散射信号光也是N帧;当传感光纤上存在扰动事件,光纤受到挤压而引起扰动事件处信号光的相位也发生改变,并通过后向瑞利散射信号光的振幅表现出来;将N帧信号曲线隔K帧作振幅差分,再取绝对值,得到N-K条振幅曲线,通过累加的曲线振幅峰值可以快速对扰动事件进行定位。其表达式为
(12)
其中:ai为采集的第i帧后向瑞利散射光的功率;A为N-K条振幅差分曲线累加的功率。由式(12)可知,振幅差分法通过隔帧相减在一定程度上起到了降噪的效果,该方法虽然简单,但其缺点也很明显,即信噪比不高。原因在于该算法中K值大小取决于被测振动信号的频率范围。对于低频信号,当K取值相对较小时,差分间隔太短,振动信号并未包含波峰和波谷,导致差值变化不明显,得到的累加效果也不明显。对于高频信号,当K取值较大时,差分间隔太长,累加次数非常少,得到的累加效果不明显。因此,振幅差分法适用范围并不广。
图4、5分别为压电陶瓷35 Hz和500 Hz频率下不同K值振动信号图。振动位置位于1 050 m处,其中位于光纤末端2 800 m处属于菲涅尔效应,不是振动信号。从图4可看出,当振动信号为35 Hz时,K取40时得到信号的信噪比最低,几乎被淹没在噪声中,随着K值逐渐增大,信噪比越高且信号越清晰。从图5可看出,当振动信号为500 Hz时,随着K值逐渐增大,信噪比逐渐降低,当K=400时信号基本被淹没在噪声中。无论信号频率是多少,K值都不宜太大或者太小,所以在进行实验时为了检测不同频率的振动信号,需要连续调整K值来获得更高的信噪比。针对振幅差分法的不足,可以学习其他更好的振动信号识别算法,实现更好的振动信号检测效果。
3.2 仿真实验
在280 m传感光纤上进行脚踩模拟实验,将脚踩模拟振动施加在传感光纤187 m处。采样率设为200 kHz,通过示波器(采样率为100 MHz)对400条连续后向瑞利散射信号进行采集。信号振幅差分图如图6(a)所示。从图6(a)可看出,187 m处有尖峰,该信号的振幅为6.87 mV,计算得到的信噪比为7.36 dB。提取该处连续的8 000个时域信号,并通过傅里叶变换得到频谱图。图6(b)、(c)分别为振动信号点的时域波形和相应的频域波形图。从图6(c)可看出,脚踩频率为100 Hz。通过脚踩模拟实验,实现了传感光纤上外部扰动事件的捕获和定位,并得到振动信号的相关信息。
将已知振动信号频率的PZT放置在传感光纤进行实验。在3 100 m的单模光纤上,位于1 284 m处放置一个压电陶瓷(PZT),并施加100 Hz频率的正弦信号。采样频率为31 kHz,通过示波器对400条连续后向瑞利散射信号进行采集。信号振幅差分图如图7(a)所示。从图7(a)可看出,振动信号尖峰位于1 284 m处,振幅为11.60 mV,通过计算得到的信噪比为9.25 dB。提取该处连续的1 000个点的时域信号,振动信号时域波形如图7(b)所示,通过快速傅立叶变换(FFT)得到PZT振动信号,振动信号频谱波形如图7(c)所示。从图7(c)可看出,第一个峰值为100 Hz对应的就是振动器施加的频率,但是在200、300、400 Hz处也各自出现一个清晰的峰值,这主要来源于压电陶瓷(PZT)的非线性响应。正常情况下,振动器施加的正弦信号的时域波形应该是正弦波,但从图7(b)时域波形的降噪曲线可看到,波谷处却出现了波峰,原因在于给振动器的正弦波施加电压时引入了高次谐波,最后傅里叶变换导致倍频的出现。

图4 35 Hz不同K值振动信号图

图5 500 Hz不同K值振动信号图

图6 在传感光纤上脚踩振动模拟仿真结果

图7 PZT振动模拟仿真结果
为了验证Φ-OTDR传感系统可以同时监测多点振动事件,同样在3 100 m的单模光纤的2个位置施加不同的振动事件。图8为2个振动事件的位置信息粗略定位结果。从图8可看出,传感光纤上274 m和1 286 m位置出现2个峰值,这2个峰值就是2个不同振动事件的峰值,振幅分别为7.29 mV和8.26 mV,傅里叶变换后频率为30、50 Hz。

图8 2个振动事件的位置信息粗略定位结果
通过实验证明了该Φ-OTDR系统多点探测的功能,但是信噪比相对还是比较低,这主要是由于实验所使用的Φ-OTDR系统灵敏度不高,以及系统光路外差检测不完全匹配。Φ-OTDR系统所使用的探测光脉宽设置为100 ns,相对应的分辨率为10 m,完全可以实现长距离传感光纤上多点扰动事件的探测,但Φ-OTDR系统也有自身的局限性,对于几十公里的长距离探测仍然有可能导致多点振动事件错误判断和定位,这就需要研究员不断地去优化和改进Φ-OTDR系统。
4 结束语
基于外差相干Φ-OTDR的全分布式光纤传感技术已经获得了很大的进步,可以实时监测光纤上的干扰事件。Φ-OTDR系统具有长距离传感方面的优势,因此,在大型项目的边境安防、高速公路监测、深海声波检测等领域起着举足轻重的作用。实验仿真结果表明,对不同扰动事件进行捕获和定位,得到了扰动事件的相关信息,也实现了传感光纤上多点振动事件的检测,但是信噪比相对较低,信号还不是很稳定。为了使Φ-OTDR传感技术更加稳定并投入实际应用,今后需对Φ-OTDR系统进行优化和改进。

