时变工作点分析算法在上海光源的应用研究

杨 星 赖龙伟 陈方舟

1（中国科学院上海应用物理研究所 上海201800）

2（中国科学院大学 北京100049）

3（中国科学院上海高等研究院 上海201204）

工作点是环形粒子加速器非常重要的测量参数，并可用于β 函数、色品、阻抗等多种关键物理参数的测量。因此，准确测量工作点对加速器稳定运行和机器优化有重要意义［1］。工作点测量一般指其小数部分的测量，即是对储存环逐圈位置信号进行频域计算，提取归一化中心频率。对于固定工作点的测量一般使用快速傅里叶变换（Fast Fourier Transform，FFT）算法。因为FFT算法的频率分辨率由计算点数N 决定，为1/N，有效计算点数越多精度越高，如为了达到归一化频率0.001 精度要求有1 000点计算数据，因此一般通过kicker加横向激励的方式增加有效计算点数以提高测量精度，但这会影响束流正常运行，只能在机器研究期间使用［2-3］。

上海光源自2012年开始运行恒流注入（top-up）模式，间隔几分钟注入一次，储存环内的束流在注入过程中会引起比较大的横向振荡，从而可利用该振荡无扰测量储存环的工作点［4-5］。但注入引起的储存环横向振荡衰减很快，只能采集到10 000 多点的逐圈数据，普通的谐波分析方法可以计算得到工作点的分辨率为0.000 1，但此方法无法追踪注入期间储存环工作点随时间的变化。对于储存环来说，注入过程是一个非常理想的观测非线性的瞬态过程，因为储存环中的磁场存在高阶项，导致束流偏心位置不同时看到的磁场强度不同，这被称为储存环的Lattice 非线性，该效应可以通过测量不同束流偏心位置相应的工作点来进行观测分析。如果能精确测定束流横向位置随时间的变化，测定瞬时工作点随时间的变化，通过分析工作点与束流位置之间的依赖关系，就可以获得储存环非线性效应的强弱信息。

本文将研究更高分辨的时变频率分析算法，以便对上海光源储存环注入过程中工作点的时变性质进行精确测量。

1 频率分析算法

频谱分析理论随着数学理论的进步，有几个比较明显的阶段。常规傅里叶方法及其适用于计算机分析的FFT 在信号处理中占据了极高的地位，连续傅里叶变换的定义如下：

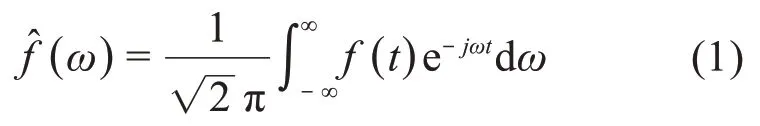
通过改变频率得到信号的幅频曲线，即傅里叶谱。但是实践表明Fourier 频谱分析并非对所有类型信号的分析都有效，被分析的系统必须是线性的；信号必须是严格周期的或者平稳的，否则谱分析结果将缺乏物理意义。但是非线性系统频率随时间的变化是十分自然的一种物理现象。因此随后诞生了短时傅里叶变换（Short-Time Fourier Transform，STFT）。

STFT 将整个长信号在时间轴上根据需求分成有可能重复，也可以不重复的若干个数据组，对数据组进行FFT 分析，从而得到随时间变化的频率分析结果。STFT的缺点是需要选择合适的窗函数，且窗是固定的，这使得短时傅里叶分析的分辨率也是固定的，不能同时满足频率分辨率与时间分辨率的要求。此外，STFT作为傅里叶分析的框架下做出的改良，频率分析能力的上限仍然受制于采样点数N，且时间分辨率和频率分辨率无法同时达到一个较优的水准。

小波变换是常用的时变频率分析算法［6］，国内已有用小波分析进行束流分析的相关研究［7］，可对信号进行局域化分析，通过选择在时间轴上具有有限能量的适当的基底信号，并和傅里叶系数一样增添系数建立函数系，对采集到的数据进行不止一维的细化分析，连续小波变换的定义如下［8］：

式中：ψ 函数即小波母函数；τ 为延时系数；a 为尺度系数，可以转化为频率，最终得到是系数(a，τ)的二维数组，这就是与傅里叶分析算法在本质上的不同。小波分析使用能量衰减的、在时域影响有限的“小”波信号作为基底，和傅里叶变换一样通过改变系数来生成一组正交基，因此小波变换能够更加精确地在局部描述所分析的信号，进而分离出信号不同时间域上的特征。小波展开的结果即小波谱是二维矩阵，两个方向分别代表了该分量所在时域和频域的位置，因此比傅里叶变换增加了一维的信息。它通过伸缩平移运算对信号逐步进行多维细化，最终达到不同频段处时间细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节，解决了傅里叶变换的频率分析能力的上限受于采样点数N制约的困难，也解决了短时傅里叶变换窗口大小固定无法动态调整时频分辨率的缺点。

1.1 小波算法

本文使用Morlet小波作为小波母函数对数据进行分析，Morlet小波是以Gauss函数作为包络的复小波，它的解析式为：

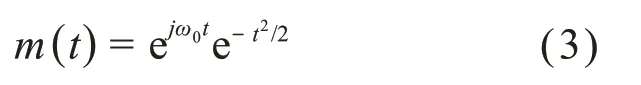
图1为Morlet小波的实数部分。

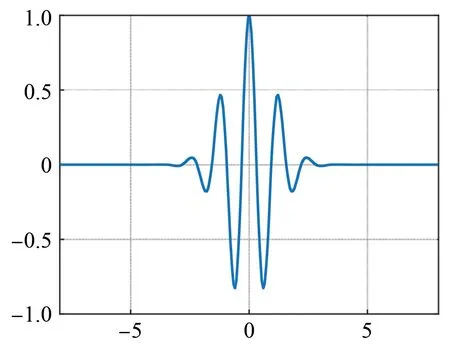
图1 Morlet母小波Fig.1 Morlet mother wavelet

Hilbert变换是将采集到的实数域的信号扩展到复数空间上，使之成为解析信号的一种方法，给定一时间连续信号x(t)，其Hilbert变换x̂(t)定义为［9］：

x(t)的解析信号定义为：

x(n)的解析信号定义为：

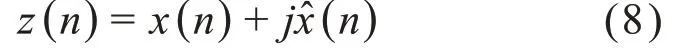
Hilbert变换具有变换前后信号频谱幅度不发生变化的性质，实部是原信号，虚部与其正交，模的大小是原信号的包络。通过该方法，我们就可以得到信号幅度随时间的变化。

对原信号进行Hilbert 变换后，与以频率为变量构建的时域上的Morlet 小波进行卷积，即可得到信号在该频率分量上随时间的相对幅值变化。对所有频率分量计算之后，即可得到二维小波谱，小波函数的频率和瞬时频率越接近时，复小波谱的模就越大，对每一个时间点上的频谱寻峰，即可近似得到该时间的瞬时频率。

1.2 NAFF算法

基本频率的数值分析算法（Numerical Analysis of Fundamental Frequencies，NAFF）是20 世纪90 年代提出来的算法，可极大提高FFT 计算分辨率。引入加速器领域后，常用于工作点分析［10］。

选取一个定长n，按照定长n 将N 点数据分成N-n+1 个短数据列，对每个短数据列进行快速傅里叶分析，得到峰值的窄带范围，之后在这个范围内，再对短数据列按照傅里叶公式：

进行频率插值，频率和原频率越相近，fn的值越大，以此寻找最接近的频率值作为该点的频率。

经验证明，当只采用32 点逐圈数据进行分析时，工作点计算分辨率就可以达到0.001［11］，因此对于长度有限的时变工作点数据，可以通过分段进行NAFF 计算的方法精确计算信号频率随时间的变化。

2 算法仿真评估

为了评估两种算法的性能，使用蒙特卡罗仿真方法对算法进行评估。

测试信号模拟储存环注入瞬态过程数据，回旋频率为694 kHz，初始幅度为1，衰减形式为指数型衰减，归一化工作点从0.220线性变化到0.221，变化方式为扫频余弦形式。

2.1 分析长度

对于NAFF算法来说，分析长度即窗口的大小，决定了时频分析的相对精度，窗口越大，时域分辨率越低，频域分辨率越高。

对于Morlet 小波算法来说，分析长度即小波分析半长度（Wave），也影响着时频分析的相对精度，Wave越大，时域分辨率越低，频域分辨率越高。

图2 是测量不确定度随分析长度的变化，纵坐标为对数坐标，可以看到，两种算法都随着分析长度的增加而提高了频率分辨率，当分析长度足够时，两种方法的分辨率均可达10-6。

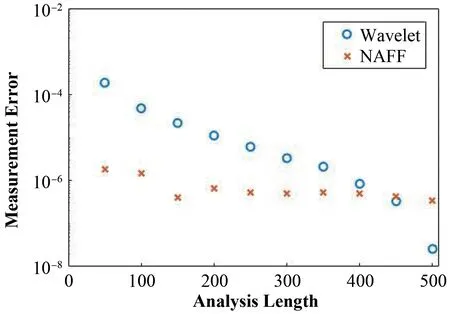
图2 测量不确定度随分析长度的变化Fig.2 Variation of measurement error with analysis length

2.2 数据信噪比

束团位置信号在采集过程中总是会包含一定程度的噪声，因此需要对算法在不同信噪比下的分析能力做测试，对两类算法的随机误差进行评估，得到数据的信噪比和频率不确定性之间的联系。

图3 是不同分析长度下测量误差随信噪比的变化。

图3 测量误差随信噪比的变化Fig.3 Variation of measurement error with SNR

可以看到，随着信噪比的增加，两种方法的频率精度都有较大的提升，且不同分析长度表现出了相似的变化规律。当分析长度确定时，Morlet 小波算法随机测量误差小于NAFF算法。

2.3 系统误差

不考虑噪声的影响，因为ejω0t的正交性，两种方法在数学上都属无偏分析，但是实际中对于有限的数据点数来说，依靠两种方法都会产生无法避免的系统误差，并且，当频率接近整数或者整数分之一时，系统误差会较其他频率有所提升，所幸在工作点设计时，会刻意避免此类数据，因此系统误差可以很小。

图4 对两种方法的频率依赖性进行了分析，分析长度固定为200，共100 个样本，可以看出两种算法的随机误差均没有明显的频率依赖性，可以对一般工作点所及的频率进行良好的分析。

图4 测量误差随分析频率的关系Fig.4 Variation of measurement error with analysis frequency

2.4 算法比较

将仿真中使用两种算法进行处理得到的一般性结果进行比较，结果如图5所示。

图5 两种算法的区别 (a)Wavelet，(b)NAFFFig.5 Difference between two algorithm(a)Wavelet,(b)NAFF

结合之前的分析，可以看出小波方法在频率分辨率和数值稳定性上有着明显的优势，信噪比较低时，小波方法的抖动远小于NAFF 方法。因此选用小波方法进行储存环工作点的提取工作。

3 算法应用

3.1 算法需求分析

上海光源储存环在注入时，会引起比较大的束流横向振荡然后逐渐衰减，图6 为利用储存环上的束流位置探测器（Beam Position Monitor，BPM）电子学设备（Libera Brilliance）采集到的上海光源储存环注入期间水平方向的逐圈数据。由于加速器四极磁铁的误差，注入期间振荡频率即工作点也会发生微小的变化，变化范围比较小。由于衰减时间较短，采集到的逐圈位置数据点数有限，如图6 所示只有10 000 点，此时使用FFT 算法只能知道整个过程平均工作点为0.225 3，并无更多信息，无法得到频率的变化。

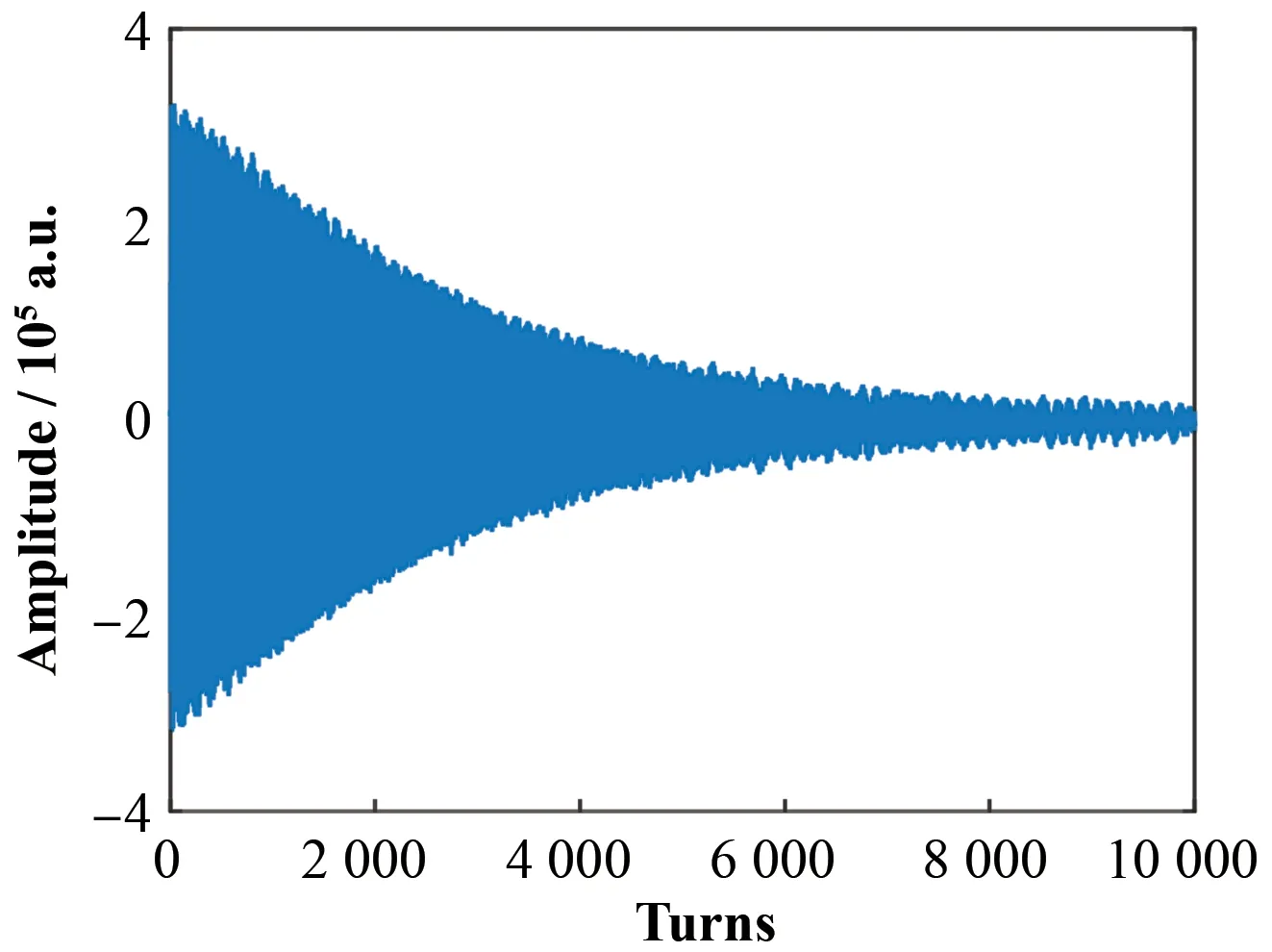
图6 上海光源储存环注入期间逐圈束流水平位置数据Fig.6 Horizontal turn-by-turn beam position data from SSRF storage ring during injection period

束流信号有明显的特征，即刚注入结束时，振幅较大（信噪比较高），工作点相对变化较大，此时对于测量的要求是高时间分辨率，低频率分辨率。当振荡衰减接近噪底时，振幅较小（信噪比）较低，此时对于测量的要求是低时间分辨率，高频率分辨率。

可见，不同的数据段对算法时间分辨率、频率分辨率要求不完全相同，如想得到尽可能好的结果，需要针对被测对象特征调整算法参数。原则上需要在工作点分辨率满足要求的前提下，使分析窗口尽可能小（提高时间分辨率）。

3.2 获取横向位置变化曲线

束团横向位置的测量存在一定的测量误差，即BPM 系统所用逐圈（Turn-by-Turn，TBT）的分辨率，对注入前后稳定的位置数据进行处理，得到横向测量位置的系统误差，逐圈位置测量分辨率为2.1 μm，对 应的随 机 噪 声峰峰值（Peak-to-Peak，PP）为7.6 μm，如图7所示。

图7 位置测量误差Fig.7 Measurement uncertainty of position

束团横向位置最大振幅的获取通过对采集到的振荡曲线用Hilbert 变换来获得。因为工作点算法的局域特性，所以求振动曲线的包络时，采用多次求包络取平均的做法，得到和工作点计算结果更为匹配的振幅。

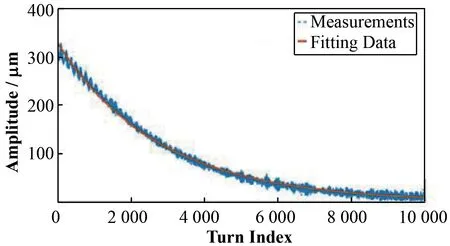
图8 信号及其包络拟合Fig.8 Signal and its envelope fitting

从图8 可以看出，Hilbert 算法很好地拟合了束团位置曲线的绝对值，可以认为该值即束团在当时的振幅。且束团在注入过程中的振幅从300 μm 迅速下降到10 μm左右，和上述测量误差进行比较，可以认为6 000点之后的采样信噪比过低，分析结果不可信，因此舍去。

3.3 确定信号分析窗口

不同分析长度下有着不同的时频分辨率，需要在满足频域分辨率的条件下，选择最小的分析长度。

通过对储存环注入瞬态过程中束团位置信号的进一步分析，使用初始振幅330 μm，噪声幅度7.6 μm，采样点数6 000，归一化振荡频率在0.225 25～0.225 35 的仿真信号进行不同分析长度的模拟比较（图9）。可以得到在10-5分辨率下，分析长度最小为200。

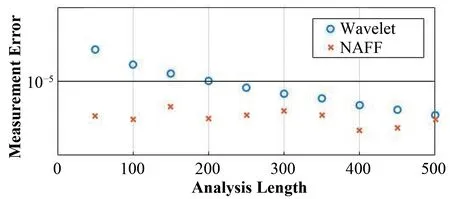
图9 测量误差随分析长度的变化Fig.9 Variation of measurement error with analysis length

3.4 分析结果

使用Morlet小波方法对上海光源储存环注入过程的动态工作点进行分析。横轴使用束团振幅，纵轴使用动态工作点。以检验该过程中的非线性效应。

选取2013 年、2014 年、2015 年、2018 年、2019年、2020 年（每年一组）数据进行处理并比较，得到图10。

后期数据点较少的原因是期间上海光源进行了注入系统及横向反馈系统的优化，阻尼时间大大缩短，采样达到1 000 点时，束团振幅已经下降到50 μm 以下，因此非线性分析仅可用1 000 圈内数据。

可以看出上海光源储存环存在明显的非线性行为，可以通过分析注入瞬态过程中的工作点漂移来评估非线性效应的强弱，通过简单的线性拟合，得到在2013 年4 月29 日，这一值为-0.000 41，在2020 年7 月8 日，这一值为0.000 7。不同时期有不同的表现，总体上非线性效应有增强的趋势。

图10 不同运行时期数据的分析结果 (a)2013，(b)2014，(c)2015，(d)2018，(e)2019，(f)2020Fig.10 Analysis results of data in different operation periods (a)2013,(b)2014,(c)2015,(d)2018,(e)2019,(f)2020

4 结语

通过仿真证明，小波分析和NAFF 算法可以进行时变工作点测量，随机测量误差小于10-5，其中小波分析算法性能好于NAFF算法。利用Morlet小波算法对上海光源储存环注入引起的束流横向振荡进行分析，可以观察到工作点随时间的变化。因此，可以利用小波分析算法和NAFF 算法在top-up供光运行的注入期间进行无扰的工作点测量，进而分析储存环非线性行为，为加速器的性能优化新增了一个有效工具。