翼型前缘对风力机翼型气动性能的影响

卜庆东，李 春，余 万，朱海天

（上海理工大学 能源与动力工程学院，上海 200093）

风能作为新能源之一，具有零污染、储量多及开发前景广阔等优势，受到了世界各国的广泛关注［1］。风力机是将风能转化为电能的旋转机械，风轮叶片是风力机的核心部件，翼型是叶片的基本要素，能够显著影响叶片气动性能，影响风力机获能效率［2-4］。

翼型几何外形对翼型气动性能有重要影响，因此通过改进翼型几何外形增加翼型升力系数、减小阻力系数及控制流动分离成为了研究热点。文献［2］中以S809 和S805 为研究对象，分析了不同程度的尾缘修剪及不同的翼型相对厚度对翼型气动性能的影响。结果表明，尾缘修剪会引起翼型最大升阻比减小，翼型相对厚度不同对翼型表面压力系数分布有显著影响。Belamadi 等［5］研究了翼型开槽对风力机翼型气动性能的影响。结果表明，槽的位置、宽度及斜率均能对翼型气动性能产生影响，且最优结构参数下的翼型槽能够改善失速条件下翼型的气动性能。Ismail 等［6］通过在翼型下表面设置半圆形凹窝和格尼襟翼修改翼型轮廓以增大翼型弯度。数值研究结果表明，这种翼型轮廓修改可以提升垂直轴风力机的扭矩，进而提升功率。Olsman 等［7］对上表面带有腔体的NACA0018 翼型进行了数值模拟。结果表明，腔体产生了反向旋转涡并与前缘涡互相抵消，从而达到流动控制效果，且在大攻角时带有腔体的翼型具有较高的升阻比。文献［8］中研究了翼型相对厚度对襟翼翼型气动性能的影响。结果表明，翼型相对厚度增大能延迟襟翼翼型进入失速区，大厚度翼型可使襟翼周围流体流动相对稳定。

本文以水平轴风力机专用翼型S809 为基础翼型，采用曲线参数化方法修改翼型前缘吸力面及压力面型线，设计两类（修改翼型1～4）不同前缘的翼型，并分析翼型前缘对翼型气动性能及流场特性的影响，为风力机翼型前缘设计提供参考。

1 翼型参数化表达

翼型设计时需对翼型进行参数化描述，以改变控制翼型形成的参数，使翼型几何形状发生变化。本文采用型函数扰动法进行翼型参数化，该扰动是指累加到基础翼型y坐标上的变化量，新翼型的几何数据是变化量和基础翼型叠加的结果［16］。

由Raymond 和Preston 于1987 提出的Hicks-Henne 型函数法是型函数扰动法中应用较为广泛的一种，其表达式为［17］

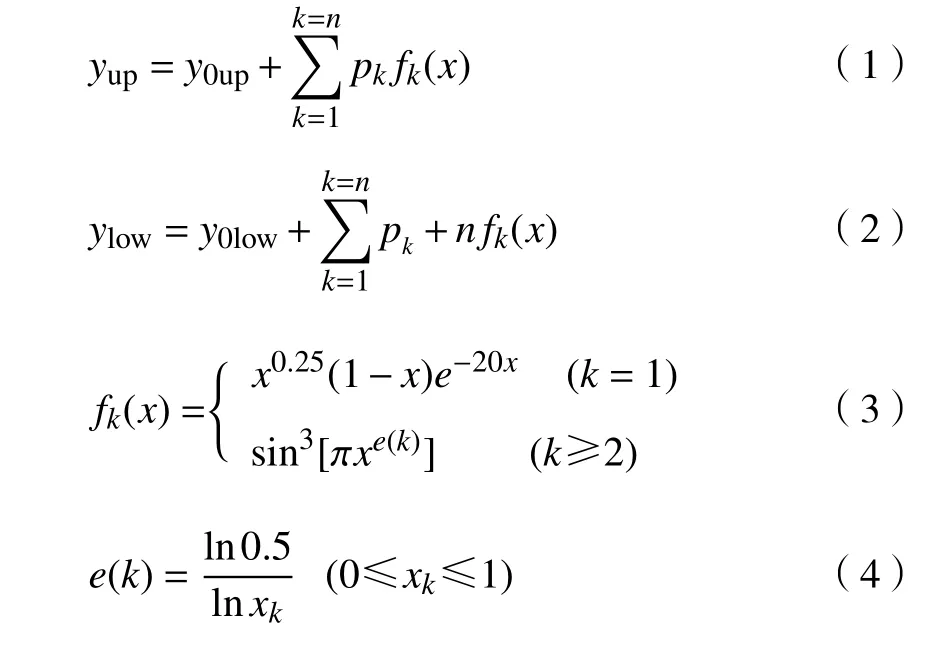
式中：yup、ylow分别为新翼型吸力面（上表面）和压力面（下力面）函数；y0up、y0low分别为基础翼型吸力面、压力面函数；n为型函数个数，根据设计要求确定；fk(x)为Hicks-Henne 型函数，又称扰动函数，它决定着扰动变化；pk为各型函数对应的系数，是翼型外形设计过程的设计变量，翼型几何设计空间大小由系数pk控制；xk为在翼型弦线上选取的节点。

当n=5 时Hicks-Henne 型函数如图1 所示，其中：f1(x)控制前缘点变化范围，f1(x)～f5(x)共同控制翼型几何外形变化幅度；c为翼型弦长。

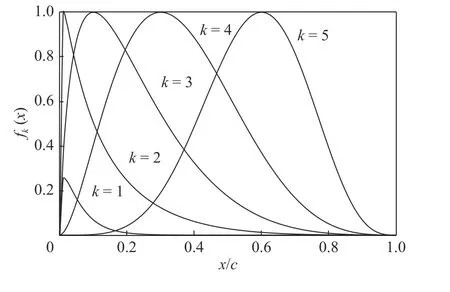
图 1 Hicks-Henne 型函数Fig. 1 Hicks-Henne shape function

由式（1）～（3）可看出，Hicks-Henne 型函数与基础翼型函数的叠加是对整个翼型弦长c上的厚度函数进行修改。本文需要对翼型前0.4c进行修改。为将扰动限制在翼型前0.4c，并保证在翼型前0.4c位置处的连续性与光滑性，对Hicks-Henne 型函数进行修正，表达式［16］为

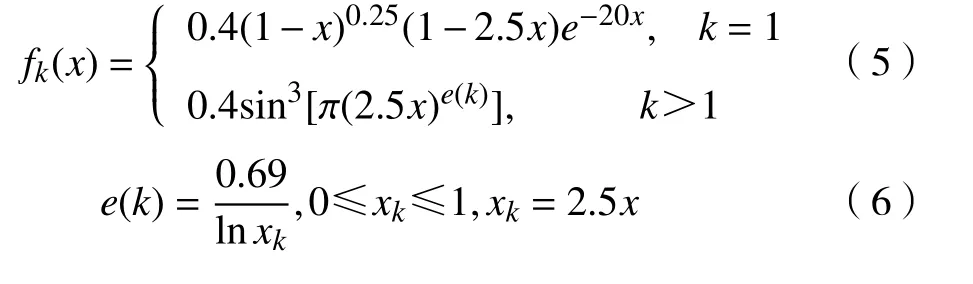
改进后Hicks-Henne 型函数如图2 所示。由图中可见，针对翼型前缘参数化，改进后的型函数继承了Hicks-Henne 型函数的优点，同时在x= 0处的扰动不再恒为0，增大了设计空间。

虽然分数是数，被称为有理数，但最初的分数是为了表达两个自然数之间的关系，主要表达两种关系，一种关系是整体的等分，另一种关系是两个线段长度的比．

图 2 改进后的Hicks-Henne 型函数Fig. 2 Modified Hicks-Henne shape function

为研究翼型前缘对翼型气动特性的影响，本文以S809 翼型为基础翼型，应用改进后的Hicks-Henne 型函数在吸力面和压力面分别取型函数系数为p1～p5与p6～p10，且设定xk（k= 2、3、4、5）分别为0.01、0.1、0.3、0.6，即改进后型函数分别放置在0.4c前的1%、10%、30%、60%处，得到两类新翼型，其中每类新翼型包含2 种变形量，其外形与S809 翼型的对比如图3 所示。由图3（a）中可以看出，修改翼型-1、2 为在保持基础翼型S809最大厚度不变的情况下使S809 翼型0.4c弦长前向上弯曲，且修改翼型-2 的向上弯曲度比修改翼型-1 的大。与修改翼型-1、2 相比，图3（b）中修改翼型-3、4 是在保持最大厚度不变的状态下向下弯曲前缘。

2 数值方法

采用翼型设计分析软件Xfoil 和商用CFD（computational fluid dynamics）软件Fluent 分别对翼型气动参数和翼型周围流场进行计算。

图 3 翼型前缘修改示意图Fig. 3 Modification of airfoil leading edge

2.1 Xfoil 数值计算

Xfoil 软件是由美国麻省理工学院Drela［17］博士于20 世纪80 年代基于Fortran 语言开发的程序软件。该软件使用有黏无黏相耦合的涡面元法，采用在翼型表面和尾迹中设置源分布来模拟黏性边界层对势流的影响。图4 为翼型表面和尾迹面元，图中翼型表面和尾迹被离散成若干面元，翼型表面分布N个面元节点，尾迹分布Nw个面元节点。每个面元有一个表示翼型表面强度 γi（1 ≤i≤N）定义的线性涡分布，每个翼型表面和尾迹面元上还有一个等强度 σi（1 ≤i≤N+Nw）的源，sˆ为沿着等分尾缘角方向上的单位矢量；tˆ为沿着尾缘缺口面元的单位矢量；S为流场。

图 4 翼型表面和尾迹面元Fig. 4 Panel of the airfoil surface and wake

Xfoil 软件较适合求解跨音速和雷诺数低的流动问题，并具有求解速度快、鲁棒性良好的优点，常用于风力机翼型的设计和分析。学者Levin 等［18］、Antunes 等［19］，国内文献［2-3］中计算翼型气动参数时求解器皆为Xfoil 软件，且文献［2］中对该软件的计算准确性进行了专门验证。本文中使用Xfoil 软件计算了文献［2］中的算例，并将CFD 计算值、Somers等［20］的实验值进行比较，结果如图5 所示，图中：CL、CD分别为升力系数、阻力系数；α为攻角。Xfoil 软件计算的CL、CD与实验值都较吻合，表明运用Xfoil 软件对风力机翼型气动参数进行计算具有较高的精度。

2.2 CFD 数值模型

采用商用CFD 软件Fluent 计算翼型流场时选择湍流模型为SSTk-ω。该模型考虑到了分离流动过程中的不平衡作用，针对动态失速的计算精度较高［21］。SSTk-ω湍流模型是Menter 在k-ω 模 型基础上发展而来，其湍流黏度 νt、湍动能k和湍动能耗散率ε 分别为［22］

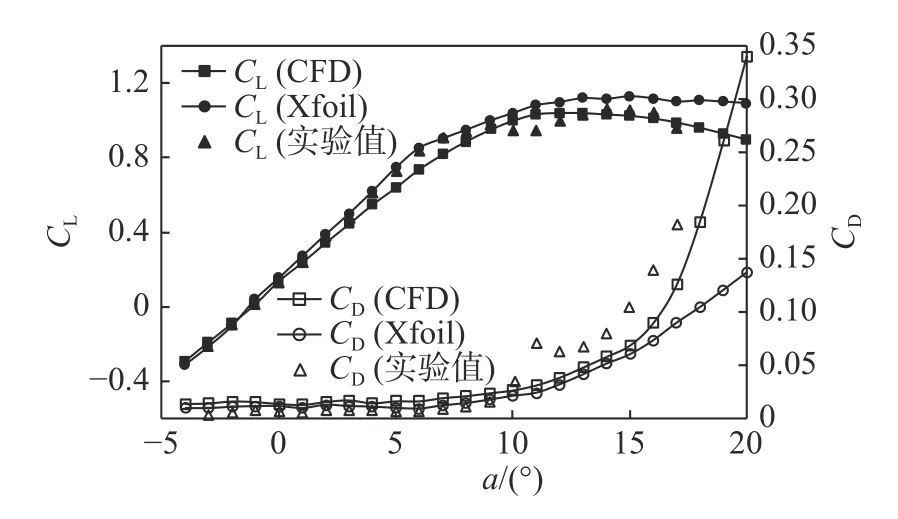
图 5 CFD 计算值、Xfoil 计算值与实验值对比Fig. 5 Comparison among CFD, Xfoil calculation results and experimental data

混合函数F1将k-ε 和k-ω两方程模型结合起来，再利用混合函数F2改进涡团黏性系数µt在壁面逆压流动的区域充分发挥k-ε模式处理自由流动和k-ω模式处理壁面约束流动的优势，能够较好地捕捉近壁面剪切层和流动分离区的流动特征［23］。

CFD 仿真计算时计算域如图6 所示。以翼型1/4 弦长处为中心划分成C 型计算域，上游来流区（半圆）半径为10c，下游尾迹区（四边形ABCD）底边宽度为15c，充分考虑了尾迹效应影响。利用网格划分软件Gambit 对翼型计算域分块生成结构网格，为能更精确地反映翼型周围流动现象，翼型壁面附近网格布置较密。图7 为翼型周围部分网格分布。整个翼型周围布置300 节点，边界层网格首层厚度为0.000 1 m，增长因子为1.08，无量纲高度y+约为1，以保证能较好地捕捉边界层内流动现象。

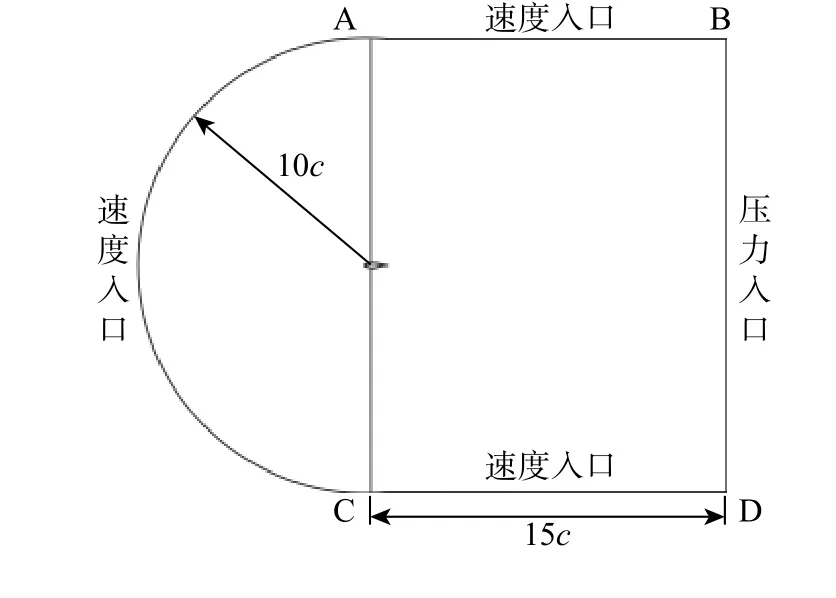
图 6 计算域及边界条件Fig. 6 Computational domain and boundary conditions

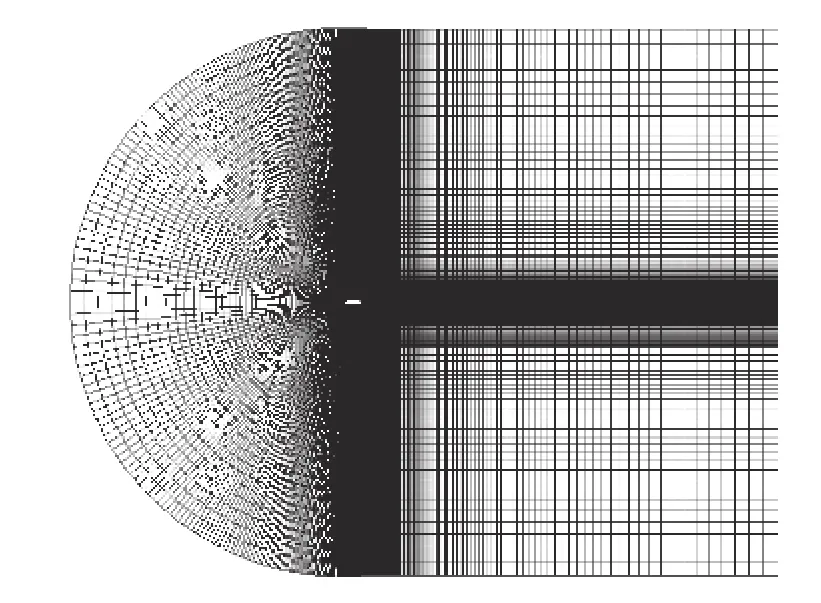
图 7 网格分布Fig. 7 Grid distribution

为验证数值方法的可靠性，计算与文献［2］及Somers 等［20］中相同工况下S809 翼型的升力系数和阻力系数。从图5 中可以看出，CFD 计算结果与实验值吻合较好，说明所采用的数值模型可较准确地计算翼型气动参数。

3 结果与分析

3.1 气动性能分析

图8 分别给出了基础翼型S809 与前缘上弯翼型［如图3（a）所示］在雷诺数为6.67 × 105、来流速度为10 m·s-1时的气动特性曲线。由图8（a）中可知，前缘上弯翼型在流动附着区和轻失速区对翼型升力系数并无明显影响，但在深失速区前缘上弯翼型使得升力系数减小，修改翼型-2 比修改翼型-1 使得升力系数减小量更大，即翼型前缘上弯度越大，升力系数减小量越大。与图8（a）相似，图8（b）中阻力系数也是前缘上弯翼型在深失速区使得阻力增大。图8（c）中在17°攻角前，前缘上弯翼型的俯仰力矩系数较基础翼型S809 的有所增大，而17°攻角后翼型进入深失速区，俯仰力矩系数有所减小。图8（d）中显示，前缘上弯翼型提前发生边界层分离转捩现象，修改翼型-2 约在3°攻角时发生，修改翼型-1 与基础翼型S809 约在5°攻角时发生；发生转捩后转捩点相对位置向前缘点移动并至某攻角时发展为完全湍流，修改翼型-2 约在7°攻角时流动发展为完全湍流，而修改翼型-1、基础翼型S809 约在攻角为9°时，说明前缘上弯翼型导致流动提前发展至完全湍流。

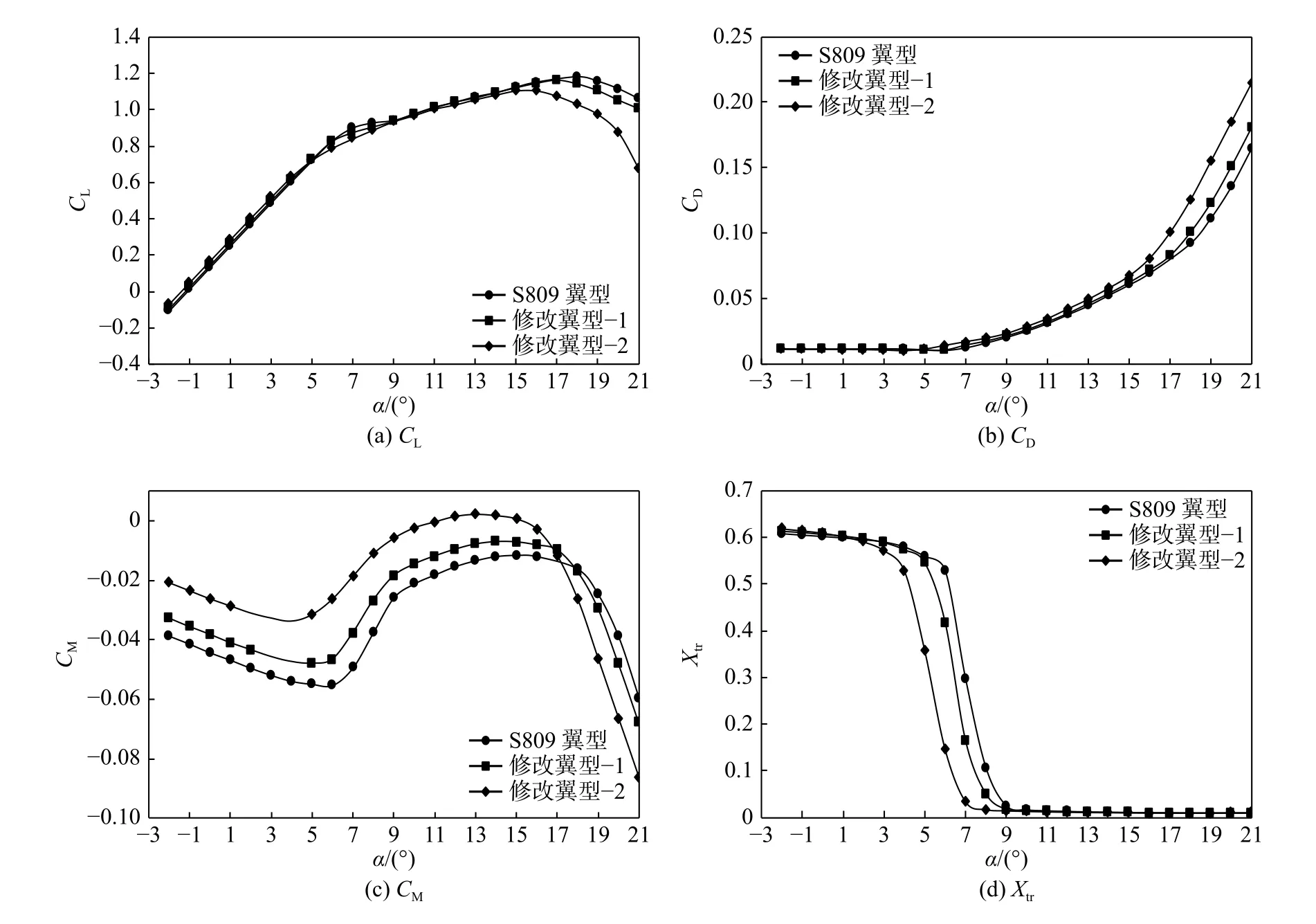
图 8 修改翼型-1、2 气动特性对比图Fig. 8 Comparison of aerodyndmic characteristics of modified airfoils-1 and -2

图9 分别给出了基础翼型S809 与前缘下弯翼型［如图3（b）所示］在雷诺数为6.67 × 105、来流速度为10 m·s-1时的气动特性曲线。由图9（a）中升力系数曲线可知，前缘下弯翼型即修改翼型-3、4 在流动附着区及失速区的11°～15°攻角范围内对升力系数影响不大，但在7°～11°攻角范围内及深失速区对升力系数影响明显，使得升力系数在此范围内增大。由图9（b）中可知，在流动附着区修改翼型-3、4 对阻力系数影响不大，在失速区修改翼型-3、4 使得阻力系数减小，且修改翼型-4 中阻力系数的减小量大于修改翼型-3 的减小量。由图9（c）中可知，在19°攻角前，前缘下弯翼型使得俯仰力矩系数减小。由图9（d）中可知，前缘上弯翼型延迟了边界层分离转捩现象的发生。基础翼型S809 约在5°攻角时开始发生边界层分离转捩现象，随着攻角增大转捩点相对位置向前缘移动，当攻角增大至约为9°时流动发展为完全湍流；修改翼型-3 在攻角约为6°时开始发生转捩现象，攻角约为10°时流动发展至完全湍流；修改翼型-4 发生边界层分离转捩现象时攻角约为7°，攻角为11°时流动发展至完全湍流。

3.2 流场特性分析

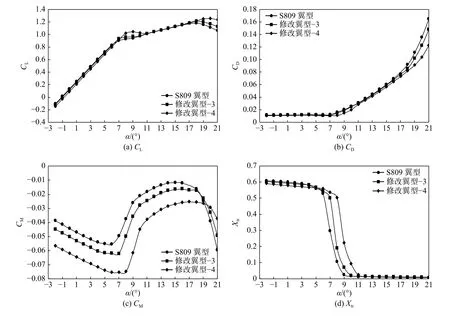
图 9 修改翼型-3、4 气动特性对比图Fig. 9 Comparison of aerodyndmic characteristics of modified airfoils-3 and -4

图10 给出了两类前缘修改翼型与基础翼型S809 的翼型表面压力系数Cp对比。由图10（a）、（b）、（c）可以看出，攻角为8°、12°、16°时前缘修改翼型对压力系数影响并不明显，只稍微影响前缘修改处翼型吸力面压力系数的大小，修改翼型-2（前缘上弯翼型）使得前缘修改处吸力面压力系数增大，修改翼型-4（前缘下弯翼型）使得前缘修改处吸力面压力系数减小。由图10（d）中可知，攻角为20°时前缘修改翼型对压力系数影响较为明显，基础翼型S809 表面压力系数变化剧烈，压力面甚至出现了负压力系数；修改翼型-2 使得翼型表面压力系数变化不再那么剧烈，翼型吸力面负压力系数有所增加，但是翼型压力面仍然出现了负压力系数；修改翼型-4 使得翼型表面压力系数变化较平稳，压力面基本保持在正压力系数范围内，吸力面基本保持在负压力系数范围内，且正压力系数、负压力系数较基础翼型S809 的都有所增加。图11 为两类前缘修改翼型与基础翼型S809 翼型流场的压力分布云图及流线图。由图中可知，随着来流攻角的增大，翼型周围压力分布发生变化，流动逐渐分离，形成尾缘涡、前缘涡及脱落涡。8°攻角时，基础翼型S809 和修改翼型-2、4 没有发生流动分离，压力分布云图及流线图无明显变化；12°攻角时，修改前、后翼型周围压力分布无明显区别，但是S809 翼型开始出现流动分离和尾缘涡。修改翼型-4 也出现流动分离，且尾缘涡覆盖范围大，分离点更靠近前缘。此时，修改翼型-4 刚出现小范围流动分离，且几乎无尾缘涡生成；16°攻角时，翼型已进入失速区，修改前、后翼型都已形成范围较广的尾缘涡及小范围的脱落涡，由脱落涡位置可看出S809 翼型较早形成脱落涡；20°攻角时，翼型已进入深失速区，S809 翼型尾部出现大范围负压，吸力面压强分布不均匀，压力面出现一定范围内分布不均匀的负压，流动紊乱，尾缘出现较大的脱落涡，吸力面中部出现范围小的涡，前缘也出现前缘涡。修改翼型-2 尾部出现更大范围高强度负压，吸力面压强分布不均匀，前缘出现范围更大的前缘涡，流动不稳定。但是修改翼型-4 尾部只出现小范围高强度负压，吸力面压强分布较均匀，无负压分布在压力面，尾缘出现尾缘涡，前缘并未出现前缘涡，流动相对稳定。

4 结 论

以S809 翼型为基础，通过翼型参数化方法改变翼型吸力面及压力面型线，设计了两类不同前缘翼型，采用翼型设计分析软件Xfoil 及CFD软件Fluent 对变形前、后翼型进行了气动特性、流场特性计算。主要结论为：

图 10 翼型前缘修改前、后压力系数对比Fig. 10 Pressure coefficient of airfoils before and after modified of the leading edge

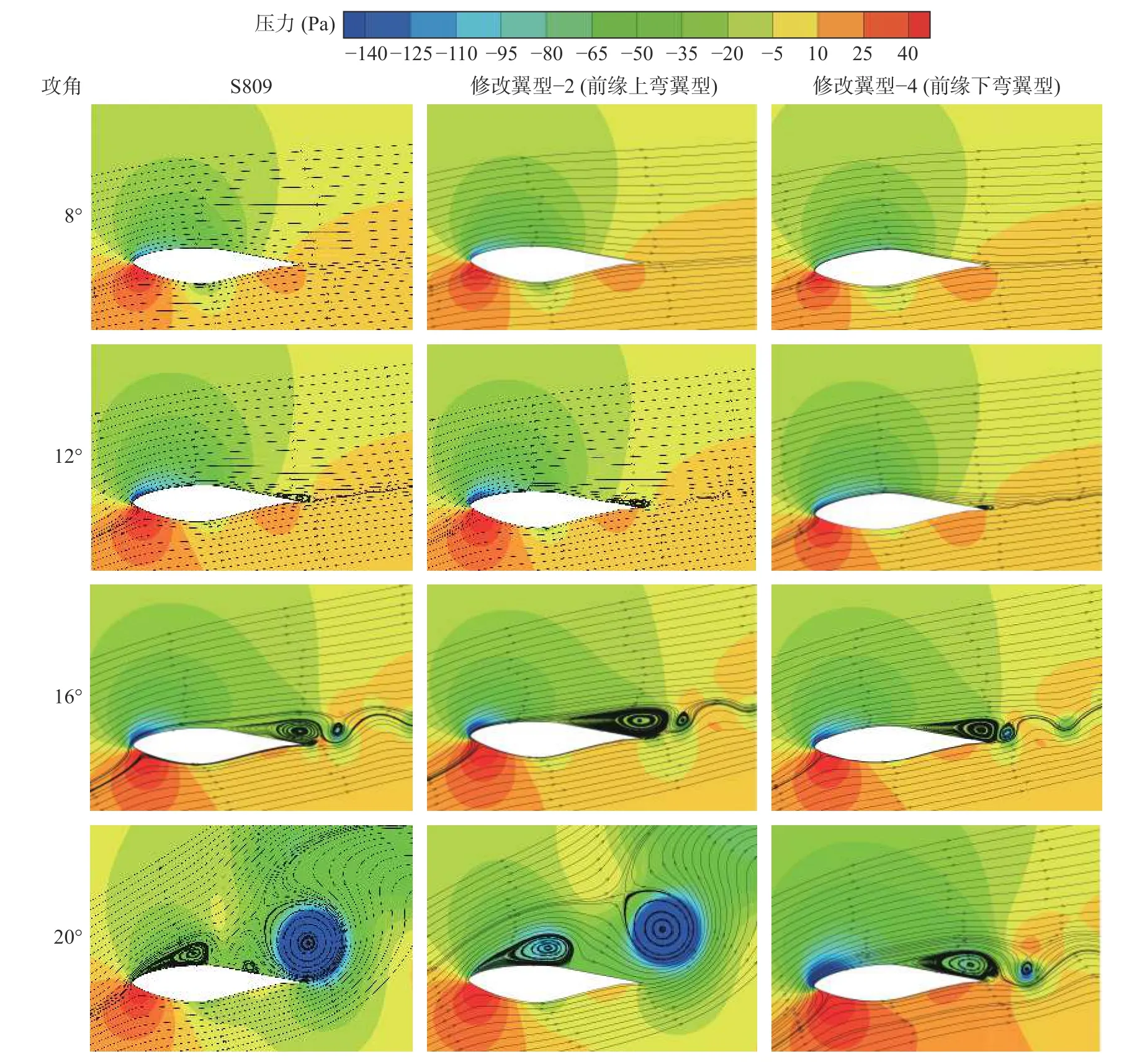
图 11 压力云图及流线图Fig. 11 Pressure contour and streamlines

（1）翼型前缘修改对翼型气动性能产生影响。前缘上弯翼型在失速区升力系数减小，阻力系数增大，俯仰力矩系数增大，转捩提前；前缘下弯翼型升力系数增大，阻力系数减小，俯仰力矩系数减小，转捩延迟。

（2）翼型前缘修改对大攻角下翼型表面压力系数产生影响，使得翼型表面压力系数分布均匀，增大了吸力面及压力面的压力系数

（3）翼型前缘上弯加剧了流动的不稳定性，使得翼型提前失速；翼型前缘下弯使得翼型周围压力分布均匀，抑制流动分离，抑制涡的形成、发展、脱落，延迟翼型失速。