换热器折流板间距和换热管排布形式对管板热应力影响分析

于春柳 任金平 廖武平

摘      要：管板作为固定管板式换热器的关键部件，其热应力是影响换热器的换热性能和使用寿命的主要因素。本文通过数值模拟方法，采用Ansys Workbench软件对某型号换热器管板进行有限元分析，研究不同折流板间距和换热管排布形式对应的管板的位移场、温度场和应力场分布。结果表明：折流板间距180 mm时管板上的最大热应力大于折流板间距108 mm和77 mm時管板上的最大热应力;3种管板排布形式的最大等效应力从小到大依次为正方形（67.273 MPa）、转正三角形（74.359 MPa）和转正方形（78.136 MPa），在实际的换热器设计中可考虑选择正方形布管方式。通过分析，揭示了折流板间距和换热管排布形式对管板热应力的影响规律，为换热器结构优化设计提供一定理论基础。

关  键  词：换热器;管板;折流板间距;换热管排布形式;热应力

中图分类号：TQ051.5       文献标识码： A       文章编号： 1671-0460（2020）11-2574-05

Analysis on the Influence of Baffle Spacing and

Tube Arrangement on Thermal Stress of Tube Sheet in Heat Exchangers

YU Chun-liu， REN Jin-ping， LIAO Wu-ping

（College of Chemistry and Chemical Engineering， Longdong University， Qingyang 745000， China）

Abstract： As one of key parts of fixed tube sheet heat exchanger， thermal stress of tube sheet is the main factor affecting the heat transfer performance and service life of the heat exchanger. In this paper， the finite element analysis of a heat exchangers tube sheet was carried out by means of numerical simulation， so the displacement field， temperature field and stress field distributions of the tube sheet corresponding to different baffle spacing and heat exchange tube arrangement were studied by Ansys Workbench software. The results showed that the maximum thermal stress on the tube sheet was greater when baffle spacing was 180 mm than those when baffle spacing was 108 mm or 77 mm. The order of the maximum equivalent stress of the three types of tube sheet arrangement was square （67.273 MPa）

Key words： Heat exchanger; Tube sheet; Baffle spacing; Heat exchange tube arrangement ; Thermal stress

 固定管板式换热器作为过程工业中常见的热交换设备，主要由管箱、壳体、管板、换热管等零部件组成[1]。其中管板是固定管板式换热器的关键部件，与壳体、换热管及管箱连接，一方面起排布换热管的作用，另一方面起分隔流体的作用，将管程和壳程流体分隔开，避免冷、热流体混合。因此，在工作过程中，管板受力情况较为复杂，须满足换热管和壳体的压力作用要求，换热管外壁与壳体内壁温差引起变形不协调产生的作用力要求，同时也要满足自身温度分布不均匀引起的作用力要求[2-3]。在这3种作用力中，换热管外壁与壳体内壁温差引起变形不协调产生的作用力和自身温度分布不均匀引起的作用力情况较为复杂，但从本质上可统一看作是管板的热应力，该热应力会使换热管与管板的接口脱开，发生介质泄露，很大程度上成为影响换热器使用寿命的关键因素[4-5]。

固定管板式换热器工作中，管板的热应力主要受温差和约束影响。为减小热应力的作用，换热器结构设计时，主要采用以下3种方法：一是单程换热器在外壳上设置膨胀节，这在一定程度上减小了该热应力，但是对于多程换热器如果只设置膨胀节是不能影响管子的相对移动的[6];二是合理设计折流板间距，通过改变壳程侧流体的流场，一方面直接使管板上壳程侧温度场分布发生变化，另一方面改变换热器换热效率，影响管板温度场，减小热应力的产生，目前研究发现，折流板间距越大壳程传热系数越小，压降越小[7-8];三是改变换热管的排布方式，此时会改变壳程流体的流动状态，影响管板上热应力的大小。本文采用数值模拟的方法，运用Ansys Workbench软件，对上述第2和第3种方法得到的固定管板式换热器模型进行有限元分析，研究不同折流板间距和换热管排方式下管板的位移场、温度场和应力场分布规律，为换热器结构优化设计提供一定理论基础。

1  建立数值模拟模型

某型号固定管板式换热器主要结构尺寸见表1。零件部件采用0Cr18Ni9材料，壳程介质为液态甲烷。选择单弓形折流板，根据最小折流板间距为壳体直径1/3～1/2规定的要求，取4块折流板间距180 mm、6块折流板间距108 mm、8块折流板间距77 mm 3种间距[9]。29根换热管排布成转正三角形、正方形和转正方形3种形式。

三维模型建立过程中在不影响模拟结果的前提下对管板、筒体等主要部件做适当的简化，忽略个别零部件。由于管板结构具有对称性，取整体结构的1/2模型进行分析。在计算过程中对模型做了以下几个方面的处理：

1）不考虑材料的各向非同性，忽略对整体影响很小的不确定因素，将模型视为对称模型，并在分析中施加对称约束。

2）每根换热管中的流体流动状态基本相同，因此认为每根换热管的轴向温度分布大致相同。

3）换热管与管板采用强度胀接方式连接，建立模型时可以认为换热管与管板已达到接近一体的程度，合理假设彼此单元是紧密接触的，不考虑接触中产生的细节问题[10]。

4）两块管板均等效为均匀的等厚度带孔圆平板，忽略其与壳体及换热管焊接处的变化。

5）不考虑折流板与壳体连接时存在的间隙，认为彼此之间紧密贴合在一起，即只有均匀并且细微的间隙。

6）由于温度场分析和结构分析中的有限元模型的单元节点号码和单元特征都完全相同，因此热分析的计算结果可以以载荷的形式导入到结构分析中而不发生错误[11]。

2  物理模型及边界条件设定

换热器壳程内是单相流体，流动属于湍流，在流动过程中质点之间相互交换动量、能量这种属于低雷诺数且受壁面限制的流体流动符合k-ε模

型[12]。壳程流域及壳程结构均采用欧拉网格描述，其中流动分析采用四面体非结构网格单元、热分析采用SOLID90单元、结构分析采用SOLID186单元。换热过程中考虑管板壳程两侧的温差和约束是产生热应力的主要因素，故设置流域与筒体接触区域、流域与管板接触区域、流域与换热管外壁面接触区域为传热壁面，采用耦合传热模型进行描述。液态甲烷进口温度为-30 ℃、速度为10 m·s-1;压力出口处压力的大小为当地大气压;管程侧管板表面温度为30 ℃。结合分析目的和载荷特点，设定管板管程侧的温度相同，采用顺序耦合法对该结构进行热流固耦合分析，即先进行流动分析，得出壳程侧温度场分布，再将流动分析中的温度场加载到管板壳程侧进行热分析，最后结合结构特点分析管板的热应力[13-14]。

3  结果分析与讨论

3.1  折流板间距对管板热应力影响

3.1.1  位移场

图1为折流板间距影响的管板位移场分布云图。由图1可以看出，随着间距的减小、折流板数量的增多，管板最大和最小位移变形量增大，管板上最大热变形均发生在中心管孔附近，且呈现由中心向边缘降低的趋势，这是由于管板上离中心孔越远受到筒体约束越强。图1（a）可看出，4块折流板间距180 mm最大位移变形量0.177 4 mm，图1（b）中6块折流板间距108 mm最大位移变形量     0.179 7 mm，图1（c）中8块折流板间距77 mm最大位移变形量0.180 3 mm，由此可见改变折流板间距或者增减折流板数量对管板最大位移变形量有影响，但不是很明显。

3.1.2  温度场

图2为折流板间距影响的管板温度场分布云图。由图2可以看出，管板最高温度发生在管板与筒体连接处附近，管板最低温度发生在中心管孔左下方管孔区域。由图2（a）可看出，4块折流板间距    180 mm时温度最高10.045 ℃、最低-9.322 ℃;由图2（b）可看出，6块折流板间距108 mm时温度最高10.854 ℃、最低-7.112 ℃;由图2（c）可看出，8块折流板间距77 mm时温度最高10.722 ℃、最低-7.361 ℃。由此可见改變折流板间距或者增减折流板数量对管板温度场分布影响不大。

3.1.3  应力场

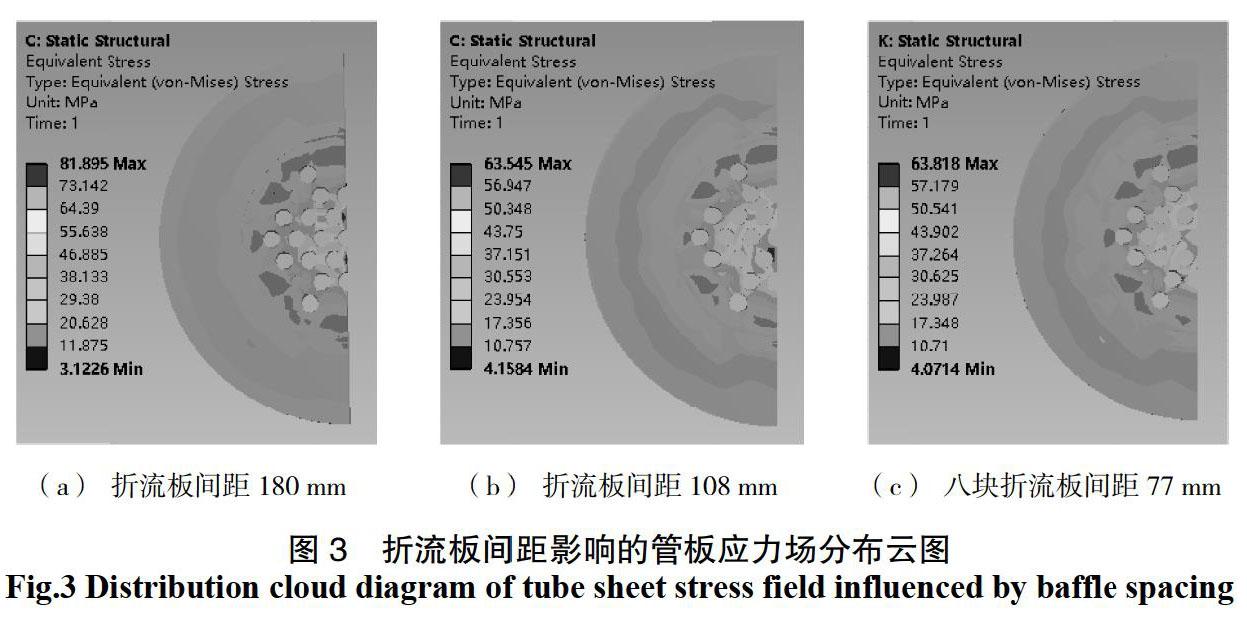
图3为折流板间距影响的管板应力场分布云图。管板最大等效应力均发生在中心管孔左下方管孔区域，固定管板式换热器在设置折流板后，低温液态甲烷经进口接管进入壳程，由于折流板的作用流体多次横向冲刷管束，不同的折流板间距造成管板变形量、管板壳程侧温度分布不同;在两者的共同作用下，管板上产生的热应力不同。

由图3（a）可看出，4块折流板间距180 mm时管板最大等效热应力81.895 MPa;由图3（b）可看出，6块折流板间距10 8mm时管板最大等效应力63.545 MPa;由图3（c）可看出，8块折流板间距77 mm时管板的最大等效应力63.818 MPa。3种不同折流板间距中，当折流板间距为180 mm时管板上的最大热应力大于另外两种情况。

3.2  换热管排布方式对管板热应力影响

6块折流板间距108 mm的换热器换热管选用转正三角形、正方形和转正方形3种排布方式，对管板分别进行数值模拟分析。

3.2.1  位移场

图4为排布方式影响的管板位移场分布云图。当换热管的排布为转正三角形设计时，管板上的最大变形量为0.175 9 mm，大于其他两种排布方式，最大变形发生在中心换热管管孔附近，且呈现由中心向边缘降低的趋势，最大变形发生位置与不同折流板间距的分析结果不同。转正三角形和正方形布管的管板最大变形发生在中心管孔附近，转正方形布管的管板的最大变形发生在管板边缘处。

3.2.2  温度场

图5为排布方式影响的管板温度场分布云图。当换热器的换热管为正方形排布式时，其管板壳程侧最大温度为10.949 ℃，发生在管板靠近壳体的布管区域边缘附近，此处温度值与其他两种情况相比较大;最小温度为-5.6176 ℃，位于中心换热管管孔附近。3种排布方式的管板温度分布均是中心低，边缘高，从中心向边缘呈现增加趋势。

3.2.3  应力场

图6为排布方式影响的管板应力场分布云图。由图6可以看出，管板的最大等效应力从小到大依次为正方形、转正三角形和转正方形排布，最大等效应力分别为67.273、74.359、78.136 MPa。最大应力均发生在管孔区域，说明管板应力受换热管温度和约束的影响要比管板受壳体温度和约束的影响严重。在实际的换热器设计中，为了减小热应力，可以考虑选择正方形布管方式。

4  结 论

管板作为换热器的关键部件，一方面起排布换热管的作用，另一方面起分隔流体的作用，其热应力对换热器的换热性能及使用寿命具有一定的影响。本文采用Ansys Workbench软件，对某型号换热器不同折流板间距和换热管排布方式对管板热应力影响进行有限元分析，研究管板的温度场、应力场和位移场分布。

改变折流板间距或者增减折流板数量对管板位移场和温度场分布有影响，但不是很明显。4块折流板间距180 mm时管板上的最大热应力大于另外两种情况，最大等效热应力81.895 MPa。6块折流板间距108 mm的換热器当换热管的排布为转正三角形设计时，最大变形量为0.175 9 mm，大于正方形和转正方形排布形式，最大变形发生在中心换热管管孔附近，由中心向边缘降低;3种排布方式的管板温度分布均是中心低，边缘高，从中心向边缘呈现增加趋势;最大应力均发生在管孔区域，管板应力受换热管温度和约束的影响要比管板受壳体温度和约束的影响严重。在实际的换热器设计中，可以考虑选择最优折流板间距和正方形布管方式。

参考文献：

[1]庄严，吕明璐，张瑶，等. 固定管板式换热器强度分析与评定[J]. 当代化工，2018，47（3）：566-568.

[2]陈一鸣，王宏，王兆蕊，等.固定管板式换热器管板的应力分析和强度评定[J].石油化工设备技术，2018（6）：15-18.

[3]陈杰，纪博文，庄大伟，等.绕管式换热器管板的有限元应力分析与结构优化[J].化工学报，2018，69（S2）：128-134.

[4]陈慕天，谢禹钧，张芳瑶. 固定管板式换热器管板的有限元分析[J]. 当代化工，2014，43（7）：1227-1229.

[5]于春柳，郑旭东，任金平，等.固定管板式换热器管板热应力分析及控制措施[J]. 化工机械，2019，46（2）：210-212.

[6]钱颂文.换热器设计手册[M].北京：化学工业出版社，2002.

[7]王庆峰，庞鑫，赵双.管壳式换热器传热效率影响因素及数值模拟分析[J].石油机械，2015，43（10）：102-107.

[8]SOLTAN B K， SAFFAR-AVVAL M，DAMANGIR E.Minimizing capital and operating costs of shell and tube condensers using optimum baffle spacing[J]. Applied Thermal Engineering， 2004， 24（17/18）：2801-2810.

[9]GB 151—2014，热交换器[S].北京：中国标准出版社，2015.

[10]刘园.管壳式换热器管板开裂原因研究[D].大连：大连理工大学，2014.

[11] 张姚辉.管壳式换热器的三维有限元分析[D].北京：北京化工大学，2003.

[12]丁欣硕，刘斌. Fluent17.0流体仿真从入门到精通[M].北京，清华大学出版社，2018.

[13]吕洪.对流换热下的管壳式换热器的三维有限元分析[D].北京：北京化工大学，2004.

[14]蔡宏伟.固定管板式换热器的热应力分析与结构优化[D].南昌：南昌大学，2016.