关注生之误 谋划教之变

任晓松

(苏州市吴江区教研室 215200)

纠正学生的错误,是教学中一项常规工作，在讲解学生错题时，如果只从问题的正确解答过程去分析，而不是引导学生思考，忽视对错误原因的梳理，将错失教育的良机，直接阻碍问题的根本解决．通过错题教学，不仅要让学生知道自己错了，还要让他们知道为什么错．而教师则不限于此，还应该知道其中更深层次的原因，比如知识结构的缺陷、元认知的缺陷、系统性的能力缺陷等等．

辩证地看，学生在数学课中的错误是学生对数学知识不断理解和建构过程中的正常现象．[1]重视对学生错误的成因的分析，有依据、有针对性地对学生加以引导和矫正，既是“以学生为主体”教学理念的体现，也是使这一理念得以落实的具体措施．也就是说，它兼具教学观和教学法的功能，对于一线教师来说至为有用．概括地说，下面三点对于学生认识错误和改正错误至关重要：整体性认知、一般化认知、对比与变化．

1 整体思考，注重逻辑

例1如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为．

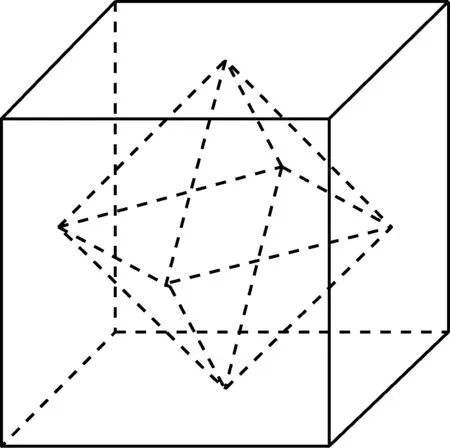
该题是2018年普通高等学校招生全国统一考试(江苏卷)的第10题，题目比较简洁，学生的解题思路也比较明确，就是将多面体分割成上、下两个一致的正四棱锥．

教学建议：整体思考的关键就是需要透过问题纷繁的表象，找到问题的本源来分析、思考．问题的解决就是矛盾论的体现，因而我们必须找到主要的矛盾，以此为抓手来思考．[2]对于这个题目，就是将多面体如何转化为可求几何体的模型，即分割为两个一致的正四棱锥求解，这个方向就是整体思考的结果．而解决问题的过程，教师应该指导学生要有层次感，要构筑解决问题的步骤，这些步骤要有明确的逻辑顺序．这个问题的解决可分为四个步骤：一、确定所求正四棱锥的底和高；二、求出其底的面积和高的值；三、将底面积和高的值代入相应的体积公式，并求解；四、求出多面体的体积．谋划步骤依赖于逻辑顺序的确立，著名数学教育学家G·波利亚在《怎样解题》一文中所提及的“拟定计划”、“实现计划”，它的作用就是让学生明晰解题步骤及要求．对于所确定的每个步骤，学生落实所需的思维比较单一、简单，有效防止思维紊乱，有助于学生解决问题的效率和正确率．这样的例子其实比比皆是，譬如对函数f(x)=sinx·cosx求导，此处运算需要兼顾乘法的求导法则和三角函数的求导公式，但逻辑顺序是求导法则在先，应用三角函数求导公式在后，所以教学时建议先用法则，得到f′(x)=(sinx)′·cosx+sinx·(cosx)′，再用求导公式，得f′(x)=cos2x-sin2x．由此可见，在整体思考的框架下，强调问题解决步骤的规划，有助于培养学生处理问题先后次序的逻辑感，而这种解题教学中培养学生的条理性，可以让学生终生受益，将极大影响其处事方式，这正是数学教学培养人逻辑特质的重要一面．

2 淡化技巧，强调通法

3 重视对比，感受变化

例3已知等比数列{an}的前n项和为Sn，S4=5S2，a2=2，则a4=．

课堂教学中的差错是不可避免的，相较于正确的单一，差错则更加丰富多彩，教师能否从差错中悟出道理，它既是对于学生教学主体地位的体现，也是对自身教育智慧的度量．著名特级教师华应龙指出，“差错的价值并不止于差错本身，而在于师生从中获得新的启迪．”[4]启迪何来？启迪来自于思考，在问题解决的过程中启发学生的哲学思考，将知识联系起来，从而弄清事物的含义，这既改变了教师的教学，也丰富学生的数学情感体验．