也谈空间向量的投影

崔 旺 保继光

(北京师范大学数学科学学院 100875)

1 向量及其数量积、投影的起源

向量作为沟通代数和几何的桥梁,在数学中有着重要的地位.1967年,美国数学家克罗威 (Michael J. Crowe,1936-) 在《向量分析的历史》[1]中指出,向量早期发展来源于数学和物理学.数学中的向量研究可以从埃及和巴比伦时期一直延伸到现代,与数的概念的发展有着紧密的联系.物理学中的向量研究也可以追溯到很久之前,与寻找代表物理量的数学概念和运算有着紧密的联系.这两大传统科学在向量研究的历史上互相交叉互相促进.

古希腊哲学家亚里士多德 (Aristotle,公元前384—322) 在《论力学》[2]中给出了速度的平行四边形法则.1687年英国科学家牛顿 (Isaac Newton,1643—1727) 在《自然哲学的数学原理》[3]中规定了力的平行四边形法则.

x=xα+xβ+xγ

向量 (vector) 一词就来源于1846年哈密尔顿在《哲学杂志》上发表的文章《论四元数》[7].哈密尔顿在《四元数讲义》[8]中,两个数量部分为0的四元数q=0+ix+jy+kz,q′=0+ix′+jy′+kz′的乘积为

qq′=-(xx′+yy′+z′)+i(yz′-zy′)+

j(zx′-xz′)+k(xy′-yx′).

显然,数量部分为0的两个四元数的乘积的数量部分是现代向量分析中相应向量数量积的负值.

1867年,苏格兰数学物理学家泰特 (Peter Tait,1831—1901) 在《四元数基础》[9]中赋予了四元数乘法的几何意义,得到了向量α,β乘积的数量部分Sαβ=-TαTβcosθ,其中Tα,Tβ分别表示向量α,β的长度,θ表示α与β的夹角.

图1

图2

美国科学家吉布斯 (Josiah Willard Gibbs,1839—1903) 与威尔逊 (Edwin Bidwell Wilson,1879—1964) 建立了向量分析理论.他们在1901年出版的《向量分析》[11]中定义：两个向量A和B的直接乘积 (direct product)A·B是向量大小A,B的乘积AB,再乘以它们之间夹角(A,B)的余弦值所获得的数量

A·B=ABcos (A,B) ,

并在此基础上定义了向量B在A上的投影 (projection) 是向量

=Bcos (A,B)a，

其中a是与A同向的单位向量.

从本质上讲,向量数量积的现代定义就是如此.此后的变化主要体现在符号上.

2 现行教材中相关内容的安排

在现行的教材中,空间向量的教学内容通常被安排在平面向量和立体几何之后,空间向量数量积的定义和运算性质都是通过类比平面向量的情形获得的,并没有给出严格的证明.在此基础上,教材引入了空间向量的投影,并把数量积的分配律应用到立体几何中线面垂直判定定理的证明.

在实际教学过程中,有些教师补证了空间向量数量积的分配律,但其中使用了线面垂直的判定定理,形成了循环论证.到底能否避免这样的逻辑循环？本文给出了肯定的答案.这需要从空间向量投影的定义说起.

(1)空间向量投影的定义

在各个版本的教材中,空间向量投影的概念可以分为三类.2003和2007人教版、2011北师版、2015沪教版的教材将空间向量的投影定义为一个数量：“已知两个非零向量a与b,我们把数量|a||b|cosθ叫做向量a与b的数量积,记作a·b,即

a·b=|a||b|cosθ，

其中θ是a与b的夹角,|a|cosθ叫做向量a在向量b方向上的投影”.

图3

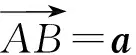
图4

图5

绝大部分教材的空间向量投影的定义都是在空间向量数量积的定义之后给出的.在这样的教材内容安排下,教师和学生忽视了投影概念的直观理解和几何意义,过多地注重利用数量积来计算投影数量,而不是利用投影去理解数量积的意义,不利于学生对空间向量投影概念的掌握.

(2)空间向量数量积分配律的证明

由于任意两个向量都是共面向量,所以空间向量的加法、减法与数乘运算性质及数量积的交换律和平面向量情形是一致的.但是,教材一般都没有注意到分配律是关于三个向量的,具有空间向量的特色,因而也没有给出具体明确的证明.在教学过程中,最常见的讲授空间向量数量积分配律的方法是类比平面向量数量积分配律的证明方法.

为了更清楚地说明问题,让我们回忆一下教材中关于平面向量数量积分配律的证明.

性质设a,b,c为平面向量,则

a·(b+c)=a·b+a·c.

图6

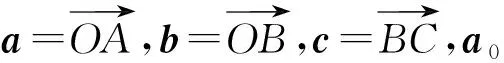
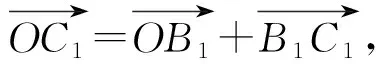
|b+c|cos a0

=|b|cos a0+|c|cos a0.

两边同时乘以|a|, 由数量积的定义可知

a·(b+c)=a·b+a·c.

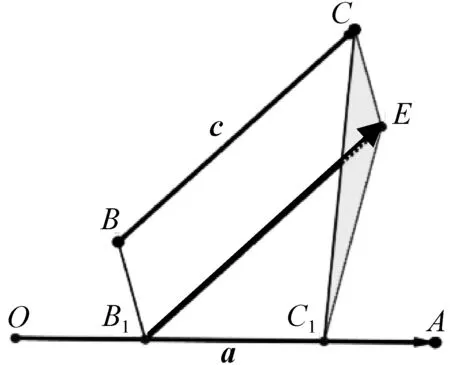
图7

在上面的证明过程中就用到了线面垂直的判定定理.同时,在有的教材中又应用空间向量数量积的分配律证明线面垂直判定定理.这样就出现逻辑循环的错误.

3 教材和教学建议

为了克服上述存在的问题,现在给出切实可行的教材编写和教学实践建议.

我们从几何角度定义投影、投影向量、投影数量.

图8

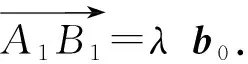
定义1不依赖空间向量的数量积,投影向量和投影数量都有相应的几何直观.

向量作为几何和代数之间的桥梁,建立上述几何直观的代数表示是一个重要的问题.下面,我们借助定义1和基本几何知识给出投影向量、投影数量的代数表示.

定理1设a,b是两个非零的空间向量,a与b的夹角为θ,b0是b的单位向量,则a在b上的投影向量是|a|cosθb0,投影数量是|a|cosθ.

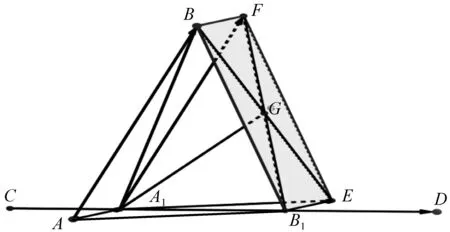
图9

(2|B1G|)2+|BE|2=2|B1E|2+2|B1B|2,

(2|A1G|)2+|BE|2=2|A1E|2+2|A1B|2,

从而

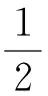
又因为B1E⊥A1B1,BB1⊥A1B1,由勾股定理上式可化简为

=|A1B1|2.

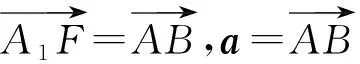
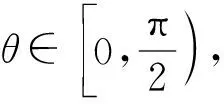
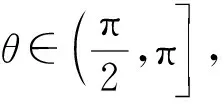
我们通过定理1清晰地看到了空间向量的投影向量、投影数量和数量积之间的关系,为数量积的教学奠定了几何基础.下面我们借助投影向量给出空间向量数量积的分配律的证明.

定理2设a,b,c为空间向量,则

a·(b+c)=a·b+a·c.

图10

=|b|cos a0,

=|c|cos a0,

=|b+c|cos a0.

|b+c|cos a0

=|b|cos a0+|c|cos a0.

两边同时乘|a|, 得

|a||b+c|cos a0

=|a||b|cos a0+|a||c|cos a0，

由数量积的定义,有

a·(b+c)=a·b+a·c.

在上述证明过程中,没有借助线面垂直的判定定理就证明了空间向量数量积的分配律.因此,教材中利用空间向量数量积分配律去证明线面垂直判定定理是合理的,不会产生逻辑循环的错误.

在空间向量的教学过程中,我们建议按照定义1给出空间向量投影向量和投影数量的几何定义,通过定理1获得空间向量投影向量和投影数量的代数表示.这样向量几何与代数的双重属性表现得非常清楚.在此基础上,进行空间向量数量积运算性质及其应用的教学.特别需要注意的是,既要避免简单地运用空间向量类比平面向量的思想,又要避免空间向量数量积分配律和线面垂直判定定理出现的逻辑循环错误.本文定理2的证明是至关重要的.