带软时间窗的多种服务需求车辆调度问题及其禁忌搜索算法研究
潘 帅 陈钰成 高 元 李文霞
(九江职业技术学院汽车工程学院1) 九江 332007) (兰州交通大学交通运输学院2) 兰州 730070)
0 引 言
对于需要专业安装的大件货物,绝大多数的电商企业将配送服务与安装服务独立分开,而货主则希望在收到货物后可以尽快获得安装服务.因此,电商企业在权衡服务质量与配送成本的同时,既要提高货主购物满意度,又要尽可能的降低配装总成本,实现总利润最大化[1].文中针对配送服务与安装服务独立分开的工作模式,研究带软时间窗的多种服务需求车辆调度问题(multi-demand vehicle routing problem with soft time window,MVRPSTW),更符合实际工作情况.
单一服务需求的车辆调度问题研究主要集中在对经典车辆调度问题加入不同约束条件或是改进求解算法等方面.谢九勇等[2]以启动车辆数、运行费用和非时间窗内服务产生的惩罚成本之和最小为目标函数,设计求解该问题的禁忌搜索算法.李阳等[3]针对模糊需求车辆路径问题,提出一种新的两阶段变邻域禁忌搜索算法,对预优化方案进行调整.李明燏等[4]构建了带软时间窗约束的异构车辆路径数学模型,在传统禁忌搜索算法的基础上加入了车辆排序准则和等级成本结构原则,设计一种新的解决车辆路径问题的算法,弥补了传统禁忌搜索算法的劣势.
多种服务需求的车辆调度是近几年才提出的热点问题.Bae等[5]研究了一种变形的车辆调度问题,即将商品的配送与安装步骤分离,安装车辆必须在配送车辆访问货主后的规定时间内到达,提高服务质量.Polat等[6]研究了取送混合车辆路径问题,即每个客户处的取送货物可以一次完成访问,也可以分两次进行送货任务与取货任务,建立了取送混合车辆路径问题的数学模型.
货物多种服务需求数学模型可看作是不同种类车辆调度问题的组合[7],即第一阶段是配送车辆调度问题;第二阶段是安装车辆调度问题.由于该数学模型的复杂程度远大于经典车辆调度问题,Kim[8]引入“分阶段”概念将该变形的车辆调度问题转化为多个子问题的组合,降低求解难度.庞海军等[9]建立以配送、安装时间最小为目标的数学模型,采用“分阶段”思想,改进遗传算法对问题进行求解.文章基于既有研究,在货物多种服务需求车辆调度模型中,加入配送车辆超时工作的折损成本、软时间窗约束、车厢装载体积约束,沿用“分阶段”的思想,将带软时间窗的多种服务需求车辆调度问题看作是两类子问题的组合:第一阶段是配送车辆调度问题;第二阶段是安装车辆调度问题.算例求解时,为增强求解性能,改进禁忌搜索算法,对当前解采用两种领域变换规则,即0-1变换、0-2变换.将改进算法的解与Lingo所得解比较,证明文章模型与算法的有效性.最后,随机生成多个案例,证明文章模型与算法可以有效处理此类问题.
1 带软时间窗的多种服务需求车辆调度问题数学模型
1.1 问题描述
货物到达当地物流园后,根据物流信息,电商企业物流中心通知该货主隶属的区域服务中心安排车辆和技工进行上门服务.仅有配送需求的货主,区域负责人只需安排一辆配送车完成配送任务;有配送和安装需求的货主,区域负责人需安排一辆配送车和一辆安装车分别完成配送和安装任务,安装车应在配送车完成配送任务后的60 min内到达货主处提供安装服务,过早或者过晚的到达货主处,均会产生惩罚成本.即已知区域服务中心和货主处的位置、货物体积、服务需求、配送服务时间窗、配送车辆车厢装载体积等信息.目标是在满足各个货主的服务需求条件下,如何调度配送车和安装车,使得整个服务过程的总成本最小.图1为多种服务需求车辆调度问题示意图.

图1 多种服务需求车辆调度问题示意图
1.2 模型假设
1) 物流园与电商企业区域服务中心的距离可以忽略不计.
2) 全部车辆从电商企业区域服务中心出发,完成任务后回到出发地.
3) 区域服务中心有足够多的可用配送车和可用安装车.
4) 配送车在货主处提供的配送服务时间可忽略不计,文章认为是连续工作,因此存在正常工作的最大时常.
5) 所有车辆在工作过程中运行速度相同,各货主处与区域服务中心直线连接.
1.3 模型符号定义
为建立带软时间窗的多种服务需求车辆调度问题数学模型,设M={0}为区域服务中心;s为配送车辆;k为安装车辆;E={1,2,…,n}为所有货主的集合,其中,每一个货主均有配送需求;A为有安装需求的货主集合,A⊂E;N为所有货主E和区域服务中心M的节点集合,N=E∪M;I为区域服务中心M和有安装需求的货主的集合,I=A∪M.
定义以下参数:qs为配送车辆s的车辆车厢装载体积,m3;W1为配送车s行驶的单位时间费用,元/h;W2为安装车k行驶的单位时间费用,元/h;Cs为启动配送车辆s产生的费用,元/辆;Ck为启动安装车辆k产生的费用,元/辆;tij为车辆从货主i到货主j的行驶时间,min;tki为安装车k为货主i提供安装服务的时间,min;ei为货主i允许配送车s到达的最早时间,min;li为货主i允许配送车s到达的最晚时间,min;Ts为配送车s正常工作的最大时常,min;di为货主i的货物体积,m3;Qt为电商企业的服务水平,即货主i的配送时间与安装时间允许的最大间隔时间,min;S1为配送车s早到达货主处所产生的时间等待成本,元/h;S2为配送车s晚到达货主处所产生的时间惩罚成本,元/h;ais为配送车s到达货主i的时间,min;bia为安装车a到达货主i的时间,min;Ei为配送车s早到达货主i处的等待时间,min;Li为配送车s晚到达货主i处的延误时间,min;δ为配送车s超时工作的车辆单位损耗成本,元/h.
定义0-1辅助决策变量vijs,为配送车s的服务顺序.
∀i,j∈N,s∈S
(1)
定义0-1辅助决策变量uijk,为安装车k的服务顺序.
∀i,j∈N,k∈K
(2)
定义0-1辅助决策变量ys,为是否启动配送车s.
(3)
定义0-1辅助决策变量xk,为是否启动安装车k.
(4)
1.4 模型数学表达
基于对上述问题的分析,建立带软时间窗的多种服务需求车辆调度问题数学模型,为
(5)
s.t.
(6)
(7)
(8)
(9)
ajs≥ais+Ei+tij,∀i,j∈N,s∈S
(10)
bjk≥bik+Li+tij,∀i,j∈I,k∈K
(11)
(12)
ais+Qt≥bik≥ais+Ei,
∀i∈A,k∈K,s∈S
(13)
ei≤ais+Ei-Li≤li,∀i,j∈I,s∈S(14)
vijs∈{0,1} ∀i,j∈N,s∈S
(15)
uijk∈{0,1} ∀i,j∈I,k∈K
(16)
ys∈{0,1} ∀s∈S
(17)
xk∈{0,1} ∀k∈K
(18)
目标函数(5)为配送、安装成本最小化,其中包括配送车和安装车的启动成本、运行成本、配送车未在规定时间内提供服务产生的惩罚成本、配送车超时工作的折损成本.约束条件:式(6)~式(7)为全部的配送、安装车均从区域服务中心出发.式(8)为每一位有配送需求的货主均有一辆配送车提供服务.式(9)为每一位有安装需求的货主均有一辆安装车提供服务.式(10)为配送车到达货主处完成配送任务后再进行下一个配送任务的顺序关系.式(11)为安装车到达货主处完成安装任务后再进行下一个安装任务的顺序关系.式(12)为配送车所载货物的体积不超过车辆车厢装载体积.式(13)为安装车应在配送车完成配送任务后的有效服务时间内到达货主处提供安装服务.式(14)为配送车在货主规定的时间窗限制内完成配送任务.
2 带软时间窗的多种服务需求车辆调度问题的禁忌搜索算法
2.1 算法简介
禁忌搜索算法(tabu search,TS)是一种亚启发式(meta-heuristic)随机搜索算法,通过模拟人的思维,利用短期记忆或者长期记忆保证算法实现全局最优解[10-11].常规流程见图2.
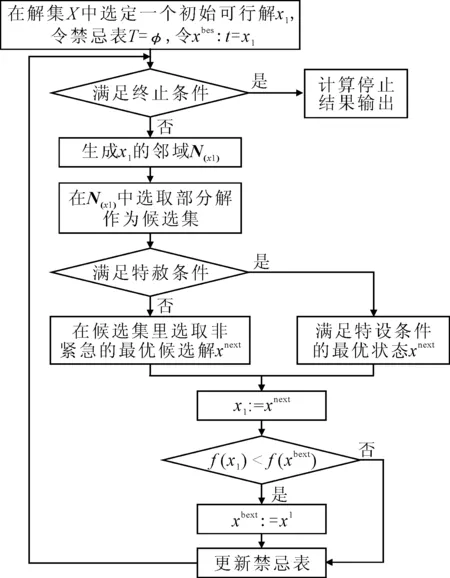
图2 禁忌搜索算法常规流程图
2.2 算法改进
2.2.1解的结构
算法中,使用一条链带来表示可行解中的一条路径顺序,每条链带中存放的数字就是路径顺序中的货主编号.文章不采用特殊的算法产生初始解,但是初始解中每条路径顺序上都有一个编号为0的地点,即电商企业区域服务中心.
2.2.2邻域变换规则
邻域变换规则(neighborhoods changed rules,NCR)可以很大程度的影响算法跳出区域局部解的能力,决定着算法的爬山能力.为增强禁忌搜索算法的求解性能,文章对当前解采用两种邻域变换规则:0-1变换、0-2变换.其中:0-1变换为在第2条路径顺序中任意选择一个编号到第1条路径顺序中去;0-2变换为在第2条路径顺序中任意选择两个编号到第1条路径顺序中去.图3为邻域变换规则示意图.

图3 邻域变换规则示意图
2.2.3禁忌表
禁忌表(tabu list)是为了确保禁忌搜索算法在搜索过程中不会出现循环现象,它可以记录之前服务的货主编号、服务顺序、或目标函数值[12].将此禁忌表设置为先入先出队列(first in first out,FIFO),即最初在禁忌表中的货主编号,在禁忌表长度超过设定值后,先被引退.
2.2.4禁忌对象
禁忌对象(tabu object)是指在禁忌表中不能发生变化的对象,文章将有序数对(ordered pair)作为禁忌对象.如有序数对(2,5)为货主编号为2与5,保证编号2的数值不大于编号5.在算法搜索过程中,若找到了最优的邻域可行解,则设可行解中两个货主编号置为2与5,将禁忌对象(2,5)存储在禁忌表里.
2.2.5禁忌长度
禁忌长度(tabu length)对禁忌搜索算法的求解效率高低与解的质量优劣有重要影响.文章将禁忌长度设置为一个定值常数.
3 算例研究及其分析
3.1 数据生成及处理
假设D为F市的物流园区,日常负责F市及周围区域的货物集散、仓储管理、商贸展览、增值加工等工作.某大型电商企业区域服务中心紧邻物流园区D,负责该企业在F市及周围区域货主的配送与安装工作.已知配送车启动成本为40元/辆,安装车启动成本为30元/辆,配送车与安装车在启动后以30 km/h的恒定速度运行(忽略加速与减速时间),单位运输成本均为5元/km.配送车的有效装载体积为45 m3,每天的有效服务时长为5 h,车辆超时工作产生的折损成本为80元/h.配送车早到达货主规定时间产生的时间等待成本为200元/h,晚到达货主规定时间造成的时间惩罚成本为300元/h.安装车及安装技师在货主处提供服务的时间均为20 min,早到不产生等待成本,晚于到达货主规定时间产生的时间惩罚成本为400元/h.根据已知的时间要求,服务中心安排车辆对25个货主提供配送与安装服务,使得服务成本最小化.服务中心与25个货主的信息见表1~2.

表1 电商企业区域服务中心数据信息

表2 货主数据信息
算例中的物流园区D与25个货主点的分布见图4.其中,“■”为区域服务中心.

图4 算例中各个节点分布图
3.2 算例结果及分析
3.2.1禁忌搜索算法及近似解
设算法的最大迭代次数为1 000,禁忌时长为100.算例的结果是需要8台配送车为25个货主提供配送服务,随后,需要5台安装车为9个货主提供安装服务.表3为近似解求得服务车辆调度方案,图5为服务车辆调度路线图.由表3可知,本次服务总成本最小为8 158.357元.在这8条配送路径中,均是在货主规定的时间内完成配送任务,并且这8辆车均在有效工作时长内工作;5台安装车也均是在配送车离开后的60 min内到达货主处进行安装作业.其中,配送车4的运行时间是最长的,为286.846 min;安装车5的运行时间是最长的,为291.567 min.

表3 近似求得服务车辆的调度方案
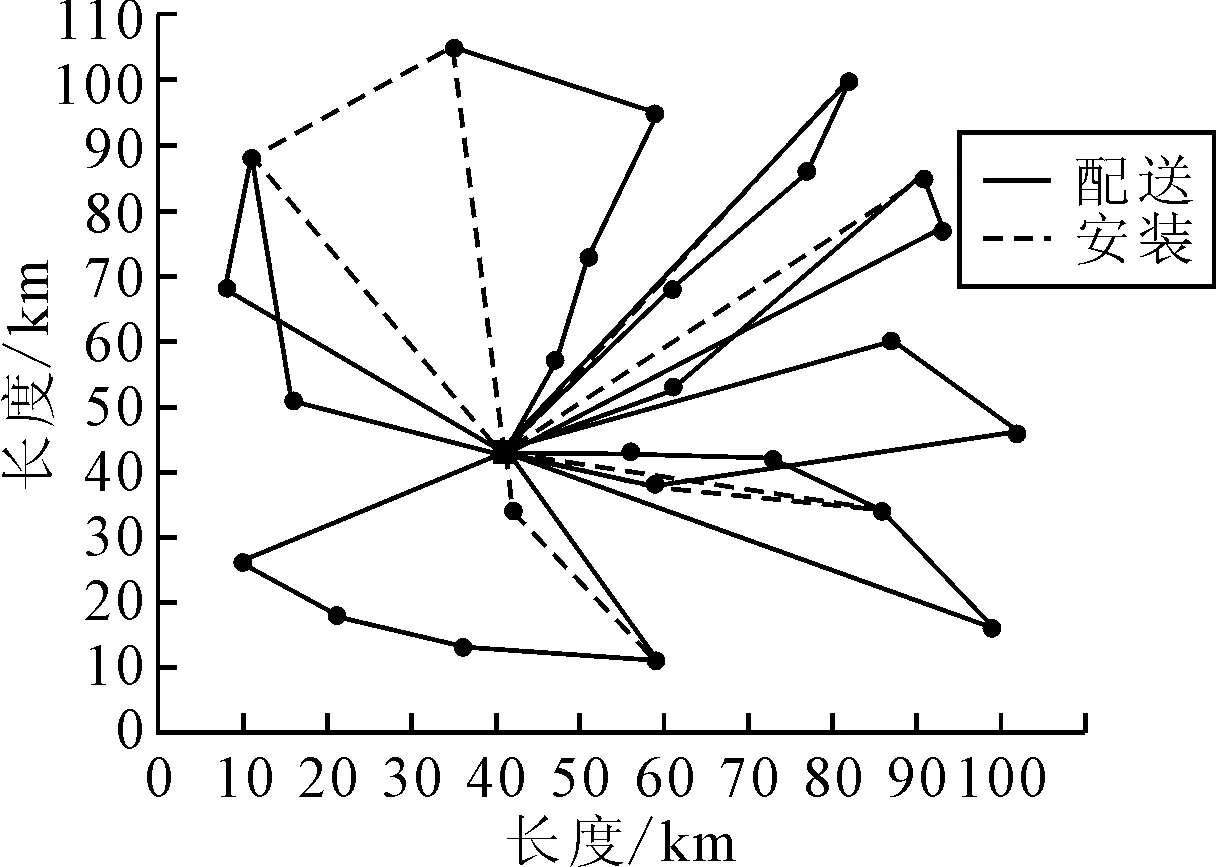
图5 近似求得的服务车辆调度路线图
3.2.2Lingo及精确解
表4为精确求得服务车辆的调度方案,由表4可知,配送与安装的总成本最小为7 053.738元.图6为精确求得的服务车辆调度路线图.在这7条配送路径中,均是在货主规定的时间内完成配送任务,并且这7辆车均在有效工作时长内工作;3辆安装车也均是在配送车离开后的60 min内到达货主处进行安装作业.其中,配送车5的运行时间是最长的,为286.644 min;安装车2的运行时间是最长的,为308.528 min.
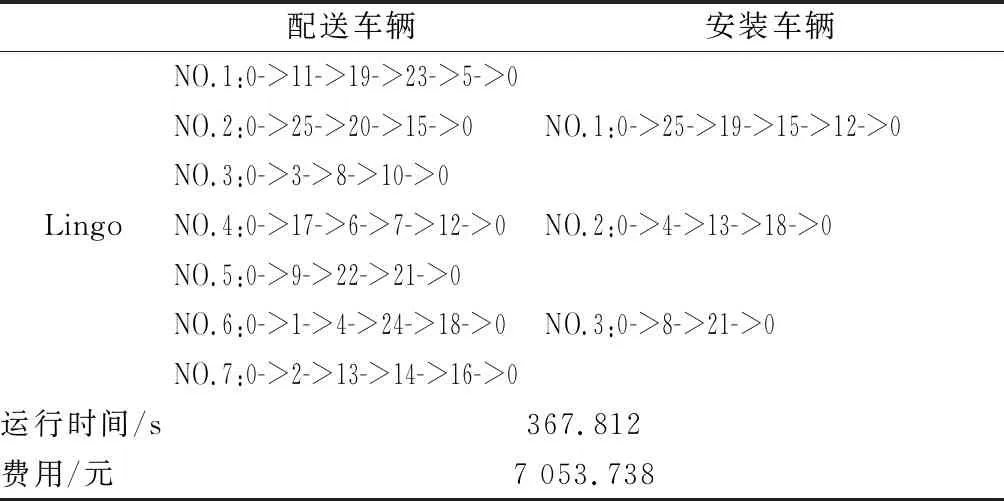
表4 精确求得服务车辆的调度方案
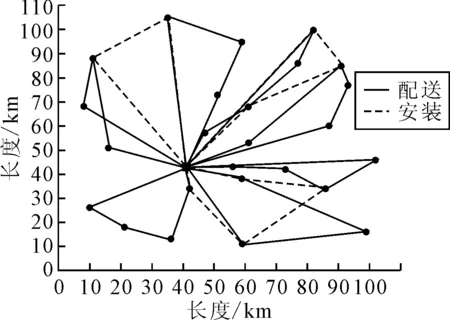
图6 精确求得的服务车辆调度路线图
3.2.3近似解与精确解的分析比较
通过使用Lingo11求解算例,需要经过367.812 s.使用禁忌搜索算法,第一阶段问题求解需要27.732 s,第二阶段问题求解需要9.376 s.引用“分阶段”概念对带软时间窗的多种服务需求车辆调度问题进行分级考虑,将它看成是两类子问题的组合,使用禁忌搜索算法对算例进行近似求解;再使用Lingo对算例进行精确求解.由表3~4可知,禁忌搜索算法得到的近似解虽没有比Lingo得到的精确解好,但可以在较短时间内得到可行解.
Lingo对于计算规模较小的问题,可以精确计算,但是对于较大规模的问题,程序运行时间较长.在实际工作中,信息数据可能会更多,因此Lingo不适用于实际工作中.禁忌搜索算法可以在较短的时间内,求得一个较优的可行解,更加适用在实际工作情景中.文章为更好的对“分阶段”近似求解方法进行有效性分析,随机生成多个规模不同的案例.其中,图7为其中一个案例的服务车辆调度路线图,可以看出“分阶段”的近似求解方法可在较短时间内找到问题的可行解.
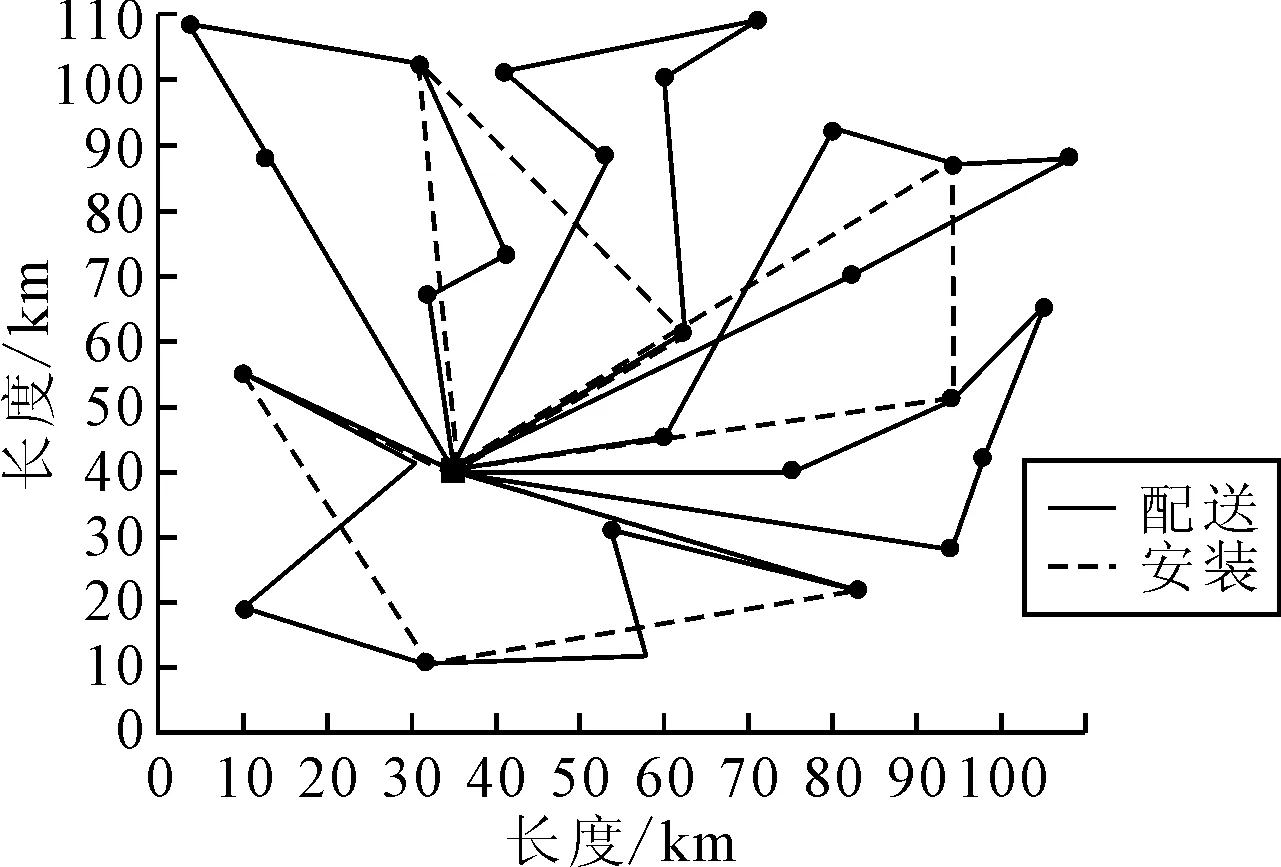
图7 随机生成案例的服务车辆调度路线图
4 结 束 语
文中研究带软时间窗的多种服务需求车辆调度问题,建立以配送费与安装费之和最小为目标函数的混合整数规划模型.将求解模型采用分层方法处理,简化原问题的复杂度,改进禁忌搜索算法对算例近似求解.将近似解与Lingo所得的精确解比较可知,配送车调度路径直接影响安装车调度路径;要保证整个服务过程中总成本最小,配送车调度路径最优解未必是整个问题的最优解;求得精确解所消耗的时间远多于近似解时间,且不能大幅降低服务总成本;在实际工作中,数据量可能更大,使用改进的禁忌搜索算法求解,可以提高服务效率,降低服务成本.
文中建立的模型与算法可以在短时间内得到带软时间窗的多种服务需求车辆调度问题的较优可行解,在未来研究中,可同时考虑两类子问题,进一步优化禁忌搜索算法,解决多种服务需求车辆调度问题.

