钢桁架拱桥施工期间标高控制可靠度研究

康俊涛 赵子越

(武汉理工大学土木工程与建筑学院 武汉 430070)

0 引 言

大跨度钢桁架拱桥的施工过程较为复杂，施工期间结构形状、温度以及所承受的荷载等方面都随时间变化，在施工过程中主梁的标高控制关系到桥梁合拢及成桥线形.

目前国内外学者对大跨度桥梁施工期间标高控制可靠度的研究，桥型均为连续刚构桥与斜拉桥，对钢桁架拱桥施工期间标高控制可靠度研究较少.常柱刚等[1]提出了一种基于SVM与蒙特卡洛法结合的方法求解了刚构桥施工期标高控制时变可靠度，孙传智等[2]建立了大跨度刚构桥挠度响应面函数，并进行施工过程中结构参数识别和时变可靠度求解，余晓琳[3]采用模糊随机等效变换的方法，结合随机有限元，求解了斜拉桥施工期间标高控制模糊随机可靠度.以上研究均未考虑温度对施工控制可靠度的影响，而温度变化对桥梁结构的受力与变形影响很大，如果在施工控制中忽略温度的影响，可能会导致控制失效概率增加.刘国坤等[4]采用基于实测温度场的数值分析方法能快速、精准地计算温度场对主梁标高的影响，颜东煌等[5]提出了一套完整的可结合施工控制参数识别和预测的温度影响现场控制和消除处理办法，但工作量巨大，施工过程中难以实现.

文中以某跨径为组合为70 m+240 m+70 m的下承式钢桁架拱桥为背景，考虑了包括温度在内的五种随机因素，采用蒙特卡罗法并结合支持向量机求解施工期间标高控制可靠度，并对几种因素进行敏感性分析.

1 工程概况

某下承式钢桁架拱桥主桥跨径布置为70 m+240 m+70 m，主桥拱肋由2片拱肋桁架和8道横联组成，2片拱肋桁架横向中心间距38.2 m.每片拱肋桁架由上弦杆、下弦杆和腹杆组成，在拱顶处上、下弦杆竖向中心间距7 m.下弦杆采用抛物线，矢高54 m，矢跨比1/4.444，上弦杆采用二次抛物线和圆曲线相结合.

本案例桥梁使用斜拉扣挂法和缆索吊装施工技术，先依次对称吊装拱肋及风撑直至拱肋合龙，再由边跨向中跨对称施工主梁至主梁合拢.本文仅考虑拱肋合拢后主梁施工期间的标高控制可靠度.

影响主梁施工期标高因素有很多，对于温度荷载，一般可分为日照温度荷载、骤然降温温度荷载及年温度变化荷载三种类型[6-7].其中日照温度荷载对局部影响较大，且多为短时急变，但若将施工控制阶段选在日出前或日出后1～2 h，可以较有效规避日照温度荷载的影响[8-9].而后两种温度荷载多作用于整体，分布状态较均匀，本文主要考虑后两种温度荷载的作用.

本文统计了2018年1月1日—12月31日工地现场温度，温度测量时间均为05:00—07:00，1年的温度分布见表1.

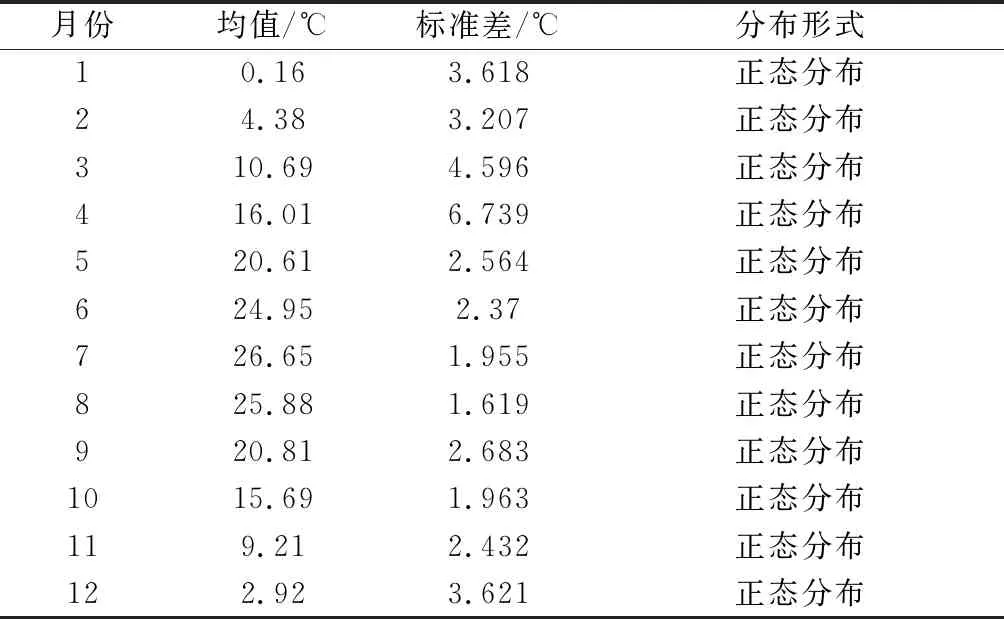
表1 温度分布统计

由表1可知，5—11月每个月温度统计标准差均小于2.6 ℃，温度荷载基本属于年温变化类型.而12—4月每个月均有温度骤降的情况，故温度统计标准差在3.2～6.8 ℃.

由于在施工过程中05:00—07:00钢桁架拱桥整体温度大致相同，故模型中仅考虑整体升降温作用即考虑温度变化产生的热应变[10].取升温降温为变量，均值为0 ℃.考虑两种温度情况，即年温变化与骤然降温，标准差分别为2.564,6.739 ℃.

选取钢梁重度、钢梁弹性模量、吊杆弹性模量、吊杆初张应力，以及温度的变化值这五类因素，根据现场的试验结果并结合参考文献[11-12]的统计结果，上述五种因素的统计特征见表2.

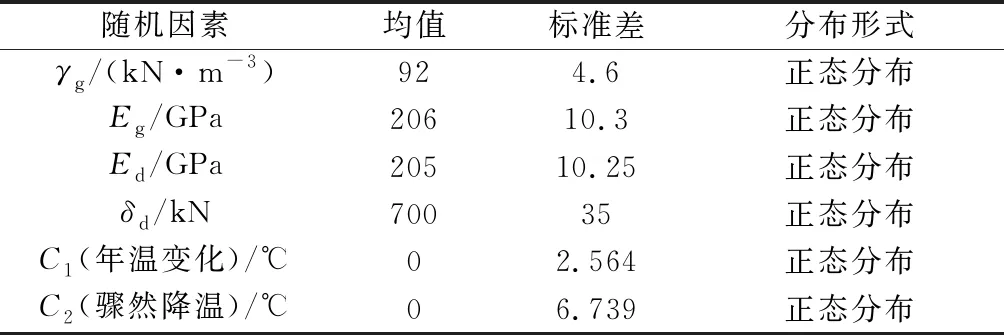
表2 施工期间五种因素统计特征

2 标高控制可靠度计算方法

本文计算标高控制可靠度指标具体步骤为：①利用拉丁超立方抽样法并结合五个随机变量的特征及概率分布产生随机样本；②利用有限元软件计算各组样本对应的目标变量；③利用样本训练代理模型，并测试其精度；④采用蒙特卡洛法并结合代理模型求解钢桁架拱桥施工期标高控制可靠度指标[13-14].

2.1 三种代理模型

传统的计算可靠度的方法如一次二阶矩法需要目标函数的显式表达式，而对于钢桁架拱桥这类较复杂的结构，施工期主梁标高的显式函数是很难得到的[15].蒙特卡洛法则需要大量抽样，利用有限元软件反复计算效率太低，故需要利用合适的代理模型来代替复杂的有限元以提高计算效率.支持向量机是基于结构风险最小原则，不受样本数量的限制，具有很出色的小样本学习能力，选取支持向量机的方法作为代理模型，并与响应面法与神经网络代理模型方法进行对比.

2.1.1响应面法

响应面法的原理是通过构造一个有明确表达式的二次多项式来拟合隐式功能函数，于是运用结构响应面方程代替有限元模型以拟合结构响应值与各影响因素之间复杂的隐式关系，就可以进一步研究结构的随机特性[16].选用不含交叉项的二次多项式.

(1)

式中：X，Y为自变量与因变量矩阵；a，bi，ci为待定系数矩阵.

为得到待定系数并取得好的拟合效果，需选择足够多的点计算Y值，并利用最小二乘法计算待定系数，

D=(XTX)-1XTY

(2)

式中：D为系数矩阵；

Y=(y1,y2,…,yk)T,k≥n.

2.1.2基于遗传算法优化的BP神经网络

BP神经网络相比二次序列响应面方法，神经网络无需给定结构功能函数就能较好拟合其响应面，避免了采用多项式不能捕捉到系统高阶相应的情况.而神经网络的训练结果与所取初始权值阈值有紧密联系，故采用遗传算法优化其权值阈值.计算流程见图1.

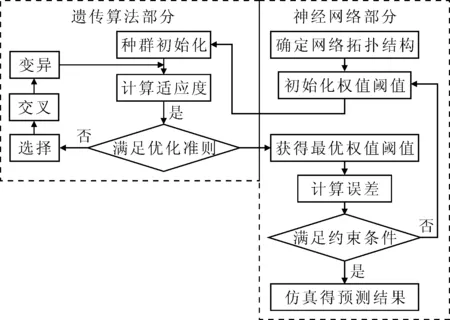
图1 遗传算法优化BP神经网络参数流程图

2.1.3支持向量机

支持向量机通过引入核函数，巧妙地解决了在高维空间中的内积运算，从而很好地解决了非线性分类问题.其中高斯核函数K(xi,xj)=exp(-γ‖xi-xj‖2)是一种径向基函数，在可靠度分析中常常被用到，使用高斯核函数的支持向量机可以获得非常平滑的估计，且其核值范围为(0,1)，使得计算过程变得简单.本文使用高斯核函数，此时变量仅为惩罚因子C与γ，使用遗传算法优化C、γ，计算流程图见图2.

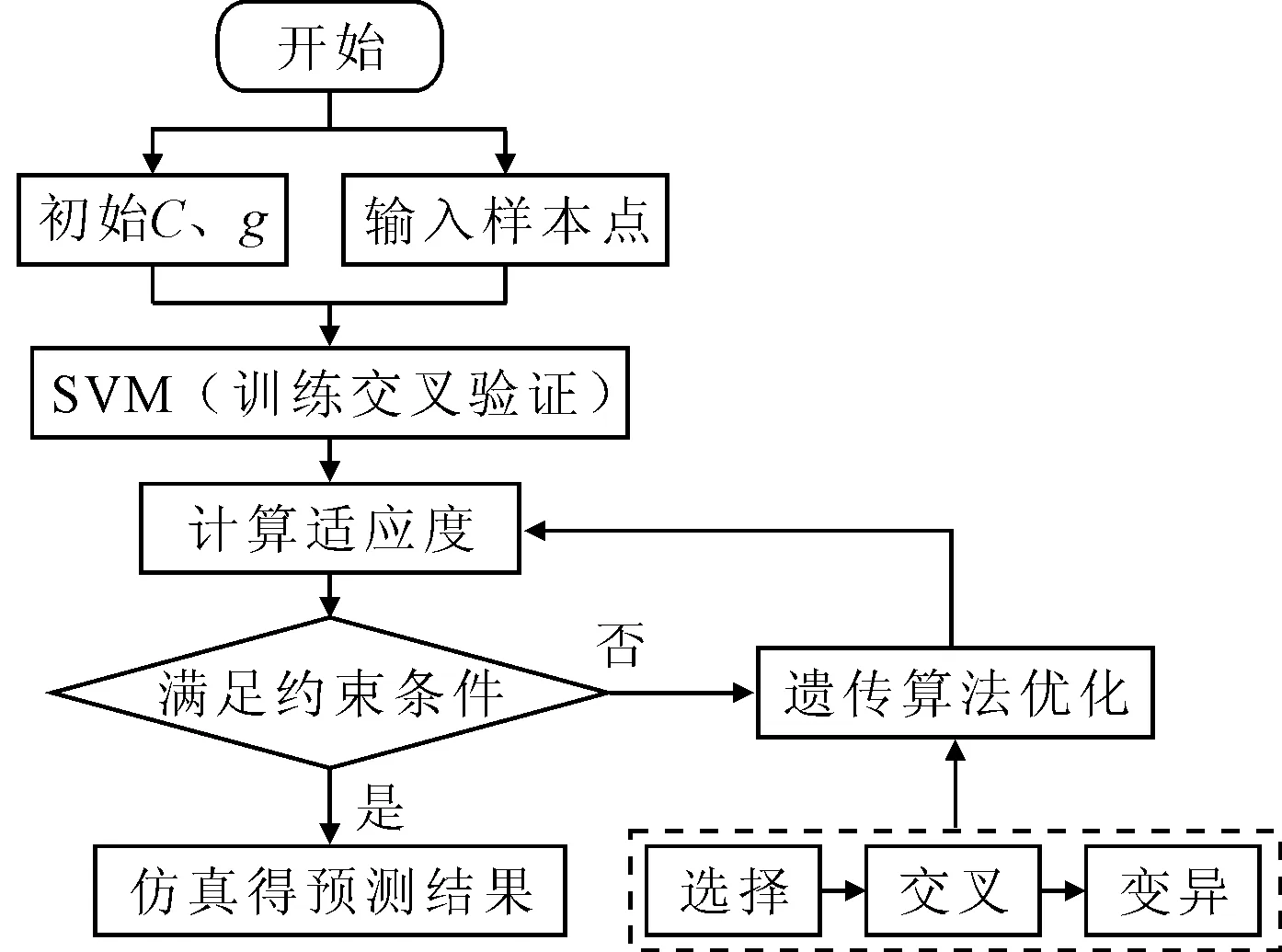
图2 SVM参数寻优流程图

2.2 某桥标高代理模型

将某桥简化为空间杆系结构模式，用桥梁结构计算分析软件Midas Civil建立，模型主梁采用空间梁单元进行模拟，其中主梁共33片，南北岸1～16#主梁以及合拢段17#主梁，分别选取4#,10#,16#主梁吊杆下锚点位置为施工过程中短悬臂、中悬臂以及最大悬臂的位置.主梁施工过程立面图见图3.

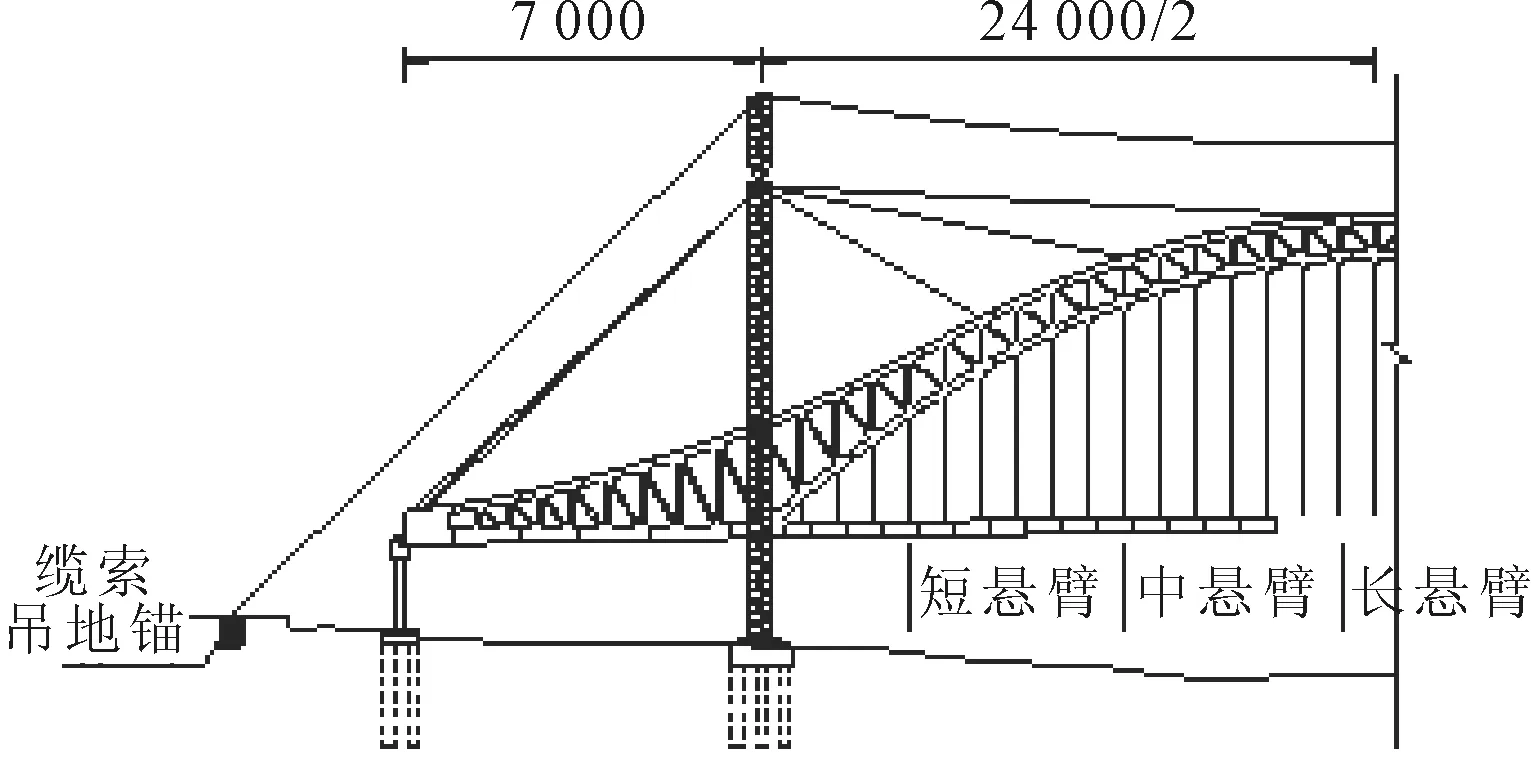
图3 主梁施工过程中桥梁立面图(单位：cm)

训练样本点的好坏直接影响到三种代理模型精度的高低，应从样本点的取值范围及分布方式着手，使样本点均匀散布在样本空间，本文所选取得五个变量钢均服从正态分布，根据3σ原则，数值分布区间[μ-3σ,μ+3σ]的概率为99.74%，能够满足分析的要求.采用拉丁超立方抽样的方法抽取100组数据，五个变量取值范围为[μ-3σ,μ+3σ](μ、σ分别为随机变量的均值与标准差)，其中温度变化的标准差选用骤然降温变化的标准差.

将上述抽样的结果带入有限元模型计算出4#梁、10#梁以及16号梁标高数据.其中随机选取80组作为训练样本，20组作为测试样本.分别使用响应面法、BP神将网络、支持向量机三种方法建立代理模型，并使用20组对训练结果进行测试，代理模型预测标高值与有限元计算标高值偏差见图4.

图4 各代理模型计算标高偏差的绝对值

由图4可知，支持向量机的模拟效果比另两种代理模型更准确，其标高预测偏差绝对值均小于1.5 mm，在容许误差范围内.代理模型预测值与抽样点的匹配程度由误差平方和S确定.

(3)

误差平方和计算结果见表3.由表3可知，支持向量机的误差平方和小于BP神经网络与响应面法故三种代理模型拟合精度由好到坏依次为基于遗传算法优化的支持向量机模型、基于遗传算法优化的BP神经网络、响应面.故采用基于遗传算法优化的支持向量机模型计算施工期标高.

表3 误差平方和计算结果

3 基于支持向量机的施工期间标高可靠度的计算

3.1 主梁标高功能函数

计算钢桁架拱桥施工期间标高控制可靠度，考虑以上影响因素变异后，根据主梁端部挠度偏差容许值，计算施工期间主梁挠度控制失效概率及可靠度指标β.

设钢桁架拱桥主梁标高控制功能函数为

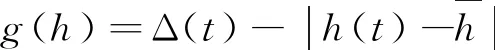
(4)

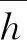
当g(h)>0时，则表示施工期主梁标高控制可靠；当g(h)<0时，施工期主梁标高控制失效.

3.2 某桥施工期间标高控制可靠度计算

利用上节训练好的支持向量机模型，输入服从各自分布的5个随机变量，利用拉丁超立方抽样的方法进行107次抽样，利用蒙特卡洛法计算各施工阶段的不同标高偏差容许值时的标高控制可靠度指标.其中施工至4#梁、10#梁、16#梁节段时，Δ(t)的预定义区间为(0.5,3)，(1，6)，(2，8)，增量均为0.2 cm.计算结果见图5.

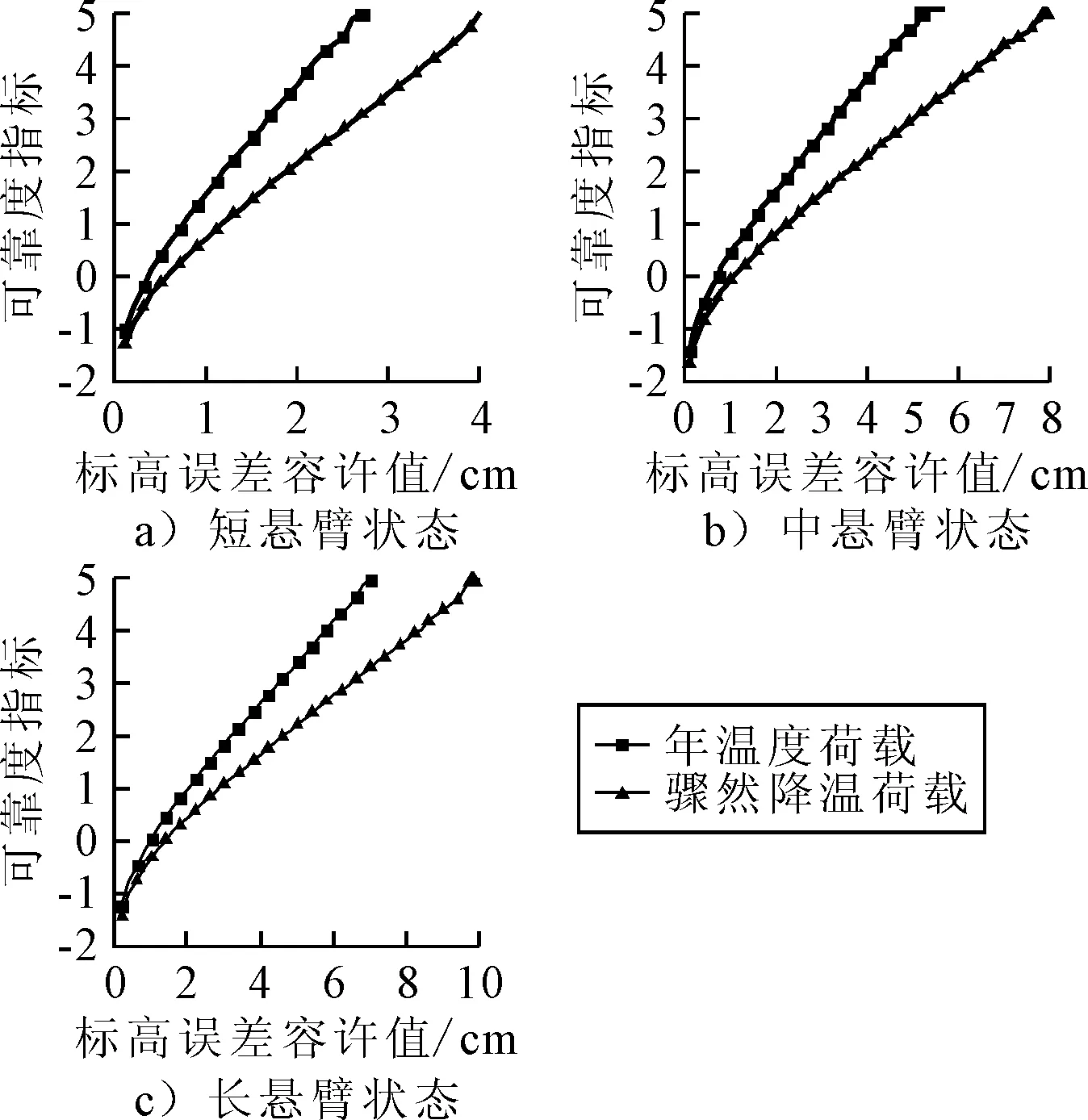
图5 各悬臂状态下标高控制可靠度

由文献[16]可知，钢梁安装梁底标高误差不得超过1 cm，而将挠度误差容许值均取为1 cm时施工至4#，10#，16#梁段标高控制可靠度指标分别为1.59，0.44，0.55，即控制失效概率为0.056，0.330，0.480，施工控制失效概率较大，尤其是进行到大悬臂状态施工控制将会很困难，必然会影响到施工进度.

于是对于不同施工阶段的标高偏差容许值应不一样，若标高偏差容许值取值过小，则会导致控制失效概率偏大，给施工控制增加难度，且影响施工进度，若标高偏差容许值取得过大，则会影响主梁合龙精度及成桥线型.目前我国规范对施工控制可靠度没有明确规定，当施工控制可靠度指标为1.65时，控制失效概率为0.05，控制失效属于小概率事件，施工控制可靠度可以满足要求，选择施工控制可靠度为1.65.

对于年温度荷载作用下，由图5可知，当施工阶段分别处于4#，10#，16#梁段，标高偏差容许值分别取1.1，2，2.8 cm时，标高控制可靠度分别为1.81，1.65，1.64，即控制失效概率为0.035，0.05，0.047.当为骤然降温荷载作用时，标高偏差容许值分别取1.6，3.1，4 cm时，标高控制可靠度分别为1.62，1.65，1.66，即控制失效概率为0.052，0.049，0.049.故钢桁架拱桥施工至不同阶段时应采用不同的标高偏差容许值，建议当温度荷载为年温度变化荷载时主梁分别处于短悬臂、中悬臂，以及长悬臂时标高偏差容许值依次取为1.1，2，2.8 cm.当温度荷载为骤然降温荷载时，标高偏差容许值最大会达到4 cm.比年温度荷载作用下的标高容许值大1.2 cm，会降低合拢精度以及影响成桥线型，故建议当温度骤然变化时应对模型进行温度的修正.

4 标高控制可靠度因素的敏感性分析

使用正交试为验设计的方法对钢桁架拱桥施工标高控制可靠度进行敏感性分析，取四水平影响因素，(γg为钢梁的重度；Eg为钢梁的弹性模量；Ed为吊杆弹性模量；δd为吊杆初张力；C为温度，其中温度均值为20 ℃)见表4.

表4 四水平影响的变异系数

同时分别选取主梁施工至长悬臂中悬臂短悬臂时，标高偏差容许值分别取为1.7，3.3，4.5 cm，保证所求可靠度不至于过大或过小.选择正交表设计出不同的试验组合，分别计算出对应的标高控制可靠度指标，极差分析计算结果见表5.

表5 L16(45)正交设计试验及结果

极差越大说明因素对可靠度指标影响越明显，由表5可知，施工至短悬臂与中悬臂时，影响因素由大到小依次为温度、吊杆初张力、钢梁容重、钢梁弹性模量，吊杆弹性模量，施工至长悬臂时，影响因素由大到小依次为温度、钢梁容重、吊杆初张力、钢梁弹性模量，吊杆弹性模量，且随着悬臂长度增加，钢梁重度该因素影响程度越大.所以施工中也应着重考虑吊杆的初张力与钢梁容重对标高控制可靠度的影响.同时由极差分析可知随着温度、吊杆初张力、钢梁重度的变异系数的增大标高控制可靠度指标下降，而吊杆弹性模量与钢梁弹性模量变异系数增加时标高控制可靠度指标的变化无明显规律，所以吊杆弹性模量与钢梁弹性模量对可靠度指标影响相对较小.

5 结 论

1) 使用支持向量机的方法拟合了结构参数与钢桁架拱桥施工期间主梁标高的关系，且拟合效果优于响应面法和基于遗传算法优化的BP神经网络的方法，提高了计算标高控制可靠度的效率.

2) 分析可知温度对钢桁架拱桥施工控制影响明显，在施工监控中不可忽略，建议施工期间1个月对模型进行温度修正，且遇到极端天气等导致温度骤变时也应对模型进行温度修正.

3) 对于该案例桥梁，当主梁处于不同施工阶段时应采用不同的标高偏差容许值，建议当主梁分别处于短悬臂、中悬臂,以及长悬臂时标高偏差容许值依次取为1.1，2，2.8 cm，对于同类型桥梁的施工控制有一定参考价值.

4) 对钢桁架拱桥标高控制可靠度影响较大的三种因素为温度、吊杆初张力、钢梁容重，施工中应着重加强吊杆的初张力与钢梁容重的质量监控，以便提高标高控制成功率.