泵站站内机组运行组合的优化研究

肖若富，龚诗雯，周玉国，张 斌，吴 荣

(1.中国农业大学北京市供水管网系统安全与节能工程技术研究中心，北京 100083；2.中国灌溉排水发展中心，北京 100054；3.宁夏自治区固海扬水管理处，宁夏 中宁 755100；4.宁夏自治区水利厅灌排中心，银川 751000)

0 引 言

许多大型泵站都采用泵站群的调水方式，在运行过程中各级泵站的流量、扬程密切相关，各泵站机组型号、台数不一，输水线路长，沿途区间分水多，实际运行中通常根据经验运行，效率低，能耗高[1]。由于机组容量高，运行时消耗的能量较大，因此，对于泵站站内运行需要进行科学、合理的机组运行组合优化[2]。

许多学者对于泵站系统优化调度问题展开了大量研究，Zessler等[3]针对一个八库七泵站供水系统，运用动态规划法通过逐步求解寻求到最佳的泵运行时间表，实现了运行成本最低。Lansey等[4]运用非线性网格仿真模型，并将泵运行台数考虑在内，实现泵站运行费用最小，能耗最低。Ostfeld等[5]通过将蚁群方案与EPANET联系起来，以系统设计和操作成本最小为目标，在满足系统要求和用户要求的情况下，以管道直径，泵站最大功率和蓄水池容量，泵站水位和蓄水池水位为决策变量，并通过两个抽水配水系统的基本运行测试该方案的可行性与灵敏性。Borkowski等[6]运用遗传算法，在满足系统要求、水位、流量的情况下，尽可能减少泵调速周期，同时参考能源价格，尽可能选择耗能较少的泵机组运行。汪安南等[7]针对大型轴流泵站，采用逆序动态规划法，以泵站运行费用最小为目标，确定泵站开机台数、机组运行角度、和泵站最优运行曲线。刘正祥等[8]采用动态规划和模拟技术相结合的方法，考虑级间的合理调配和站内机组的优化组合，针对多级泵站以能耗最小进行优化调度，取得了较为理想的结果。李世芳等[9]对梯级泵站，以机组能耗最小为目标函数，以调蓄水位为级间联系变量，采用动态规划法求解数学模型，使供水系统在最优状态工作，提高了供水单位的经济效益，具有良好的通用性。

通过以上研究可以发现，目前对于泵站系统优化调度问题求解方法包括：直接运用单一数学规划模型来研究复杂提水工程的规划调度；引入大系统优化决策模型、混合模型、计算机模拟技术、智能算法来研究复杂系统优化调度决策。本文通过建立单个机组及泵站的数学模型，以水位为决策变量，以泵站运行功率最小为优化目标，将粒子群算法与动态规划法结合起来[10,11]，求解目标函数确定各机组的运行工况，并对其进行理论分析，调整泵站站内机组的组合，实现泵站整体运行功率最小的目的。

1 研究对象

某多级提水工程共有泵站17座，安装75台水泵，其中主干有四级，东干有五级，西干有八级，各级还有支渠及蓄水池，且每级站泵型多在2～3种、水泵机组多在3台以上。为了解决用水区域的缺水问题，该大型泵站从黄河抽水，各级泵站必须满足沿途地区对灌溉和居民用水的需求。以该提水工程的总干二级泵站为研究对象，该泵站有N500-M9/675型号的泵2台、N700-M14/701T型号的泵3台、N800-M9/1028T型号的泵2台，泵站基本情况如表1所示。

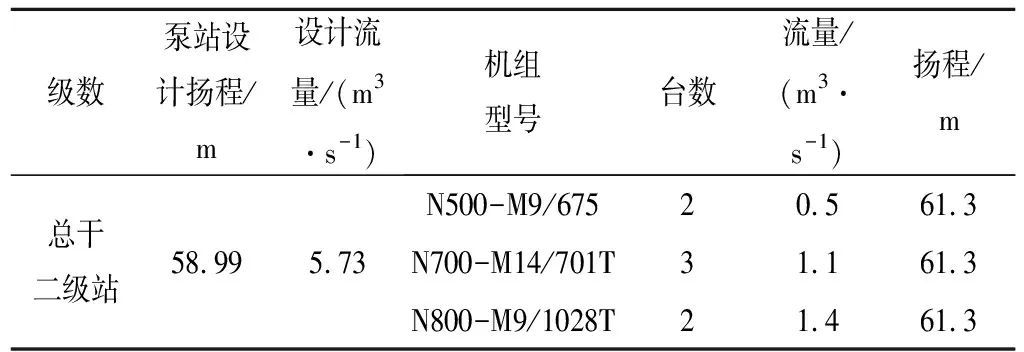
表1 泵站参数

2 模型建立与求解

2.1 泵站内机组运行的模型

单机组的运行工况不仅与水位、流量、型号等有关，还与机组的加工、运行时长及辅助设备有关，通常情况下，单机组的模型建立如下所述。

泵站运行时单机组的运行功率为：

P=ρgQH/1 000ηz

(1)

ηz=ηmηpηtηc

(2)

由水泵的性能曲线知，H与Q之间的关系为：

H=f(Q)

(3)

在泵站的运行中，我们关心的是H-Q特性曲线的高效区段，可用二次多项式插值进行拟合(其中-Q效率曲线也采用二次多项式插值)，其中a、b、c为多项式系数：

H=aQ2+bQ+c

(4)

在泵站的优化运行中，不仅要考虑水泵的特性曲线，还需要考虑系统装置的整体特性，即在克服净扬程的基础上，还要克服管路阻力，此时需要求得水泵机组的装置特性曲线，如图1、图2虚线、公式(5)所示：

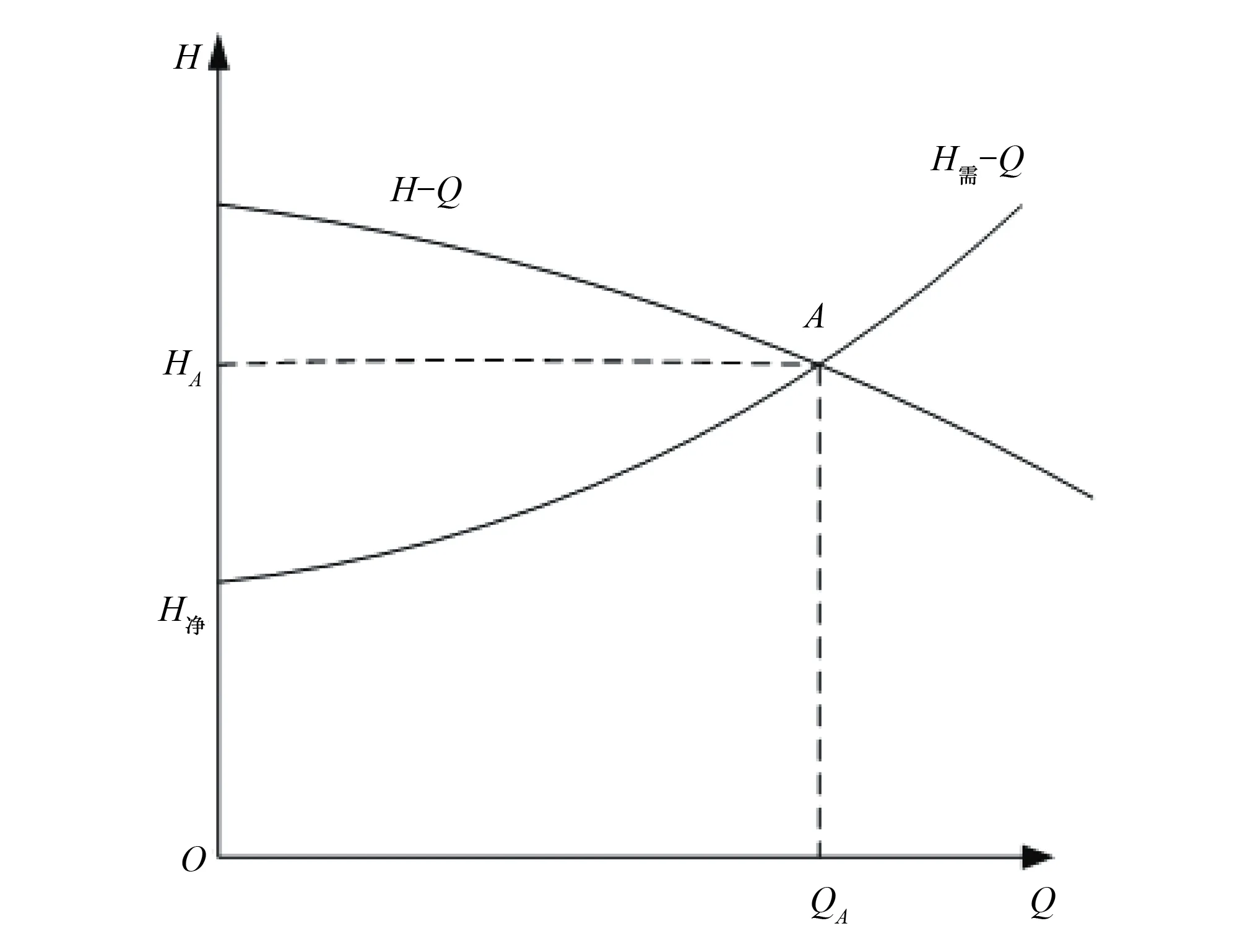
图1 图解法确定水泵工作点

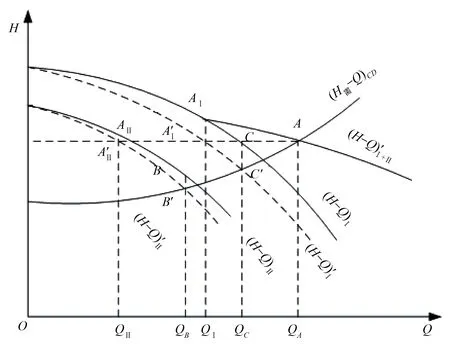
图2 水泵并联运行工作点的确定

Hz=Hj+SQ2

(5)

在泵站中，需要把水从水源逐一送至各个用水区，而输送过程中，各机组管道最终汇合至主输水管道，这时输水管道有一定的损失，故由泵站运行的原理可知，系统中泵站需要的扬程的表达式如下：

H需=H净+S0Q2

(6)

H净=H需-S0Q2

(7)

泵站中水泵机组的工作点可由机组的装置性能曲线与泵站装置性能曲线求出，即：

Hz=H净+S0Q2

(8)

2.2 站内机组运行的模型求解

站内优化主要考虑以下几个方面：

(1)流量在站内各机组间的合理分配。当泵站接到调水任务后，可根据站内各机组的实际情况，为其分配合适的流量，使得站内的能耗最少。同一泵站内，机组型号相同时可以平均分配流量，型号不同或者型号相同运行条件不同时，可在运行过程中根据计算结果进行分配。

(2)站内机组的优化组合。当站内有多台机组共同运行，扬程和流量一定时，在对流量进行科学分配的基础上，通过不同机组的组合，尽可能发挥各机组的优势，实现站内的最优化。

(3)站内各机组运行的最优工况。泵站运行时，机组型号不同，运行的工况点不同；机组型号相同时，经过长期的磨损，机组性能发生改变。故对各机组的工况点重新进行确定是非常必要的。

(4)泵站内机组组合优化运行的数学模型。泵站提水流量、扬程已知，机组不可调时，会有多种组合方式，也会有不同的运行功率，通过建立数学模型及模型求解寻优可寻求到使泵站运行最经济的组合，并求得机台数、开机种类及流量的分配，以站内总功率最小为优化目标时，如下：

目标函数：

(9)

其中：

(10)

约束条件：

(11)

0≤n≤M

(12)

Hi=hi2-hi1

(13)

hi1min≤hi1≤hi1max

(14)

hi2min≤hi2≤hi2max

(15)

Ni≤Nimax

(16)

Nijmin≤Nij≤Nijmax

(17)

Qijmin≤Qij≤Qijmax

(18)

对于不同的多级泵站及泵站群，不同的优化准则，可根据实际情况，改变数学模型及约束条件。

3 优化结果分析

各型号的特性曲线采用二次多项式插值曲线拟合，如式(19)～(27)，图3～图5：

图3 N500-M9/67性能曲线

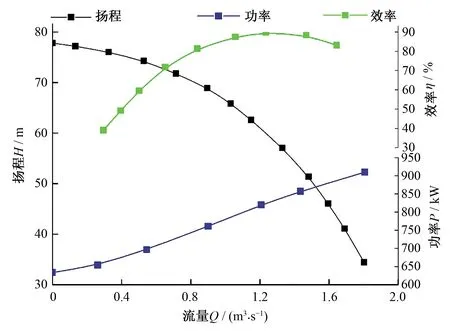
图4 N700-M14/701T性能曲线

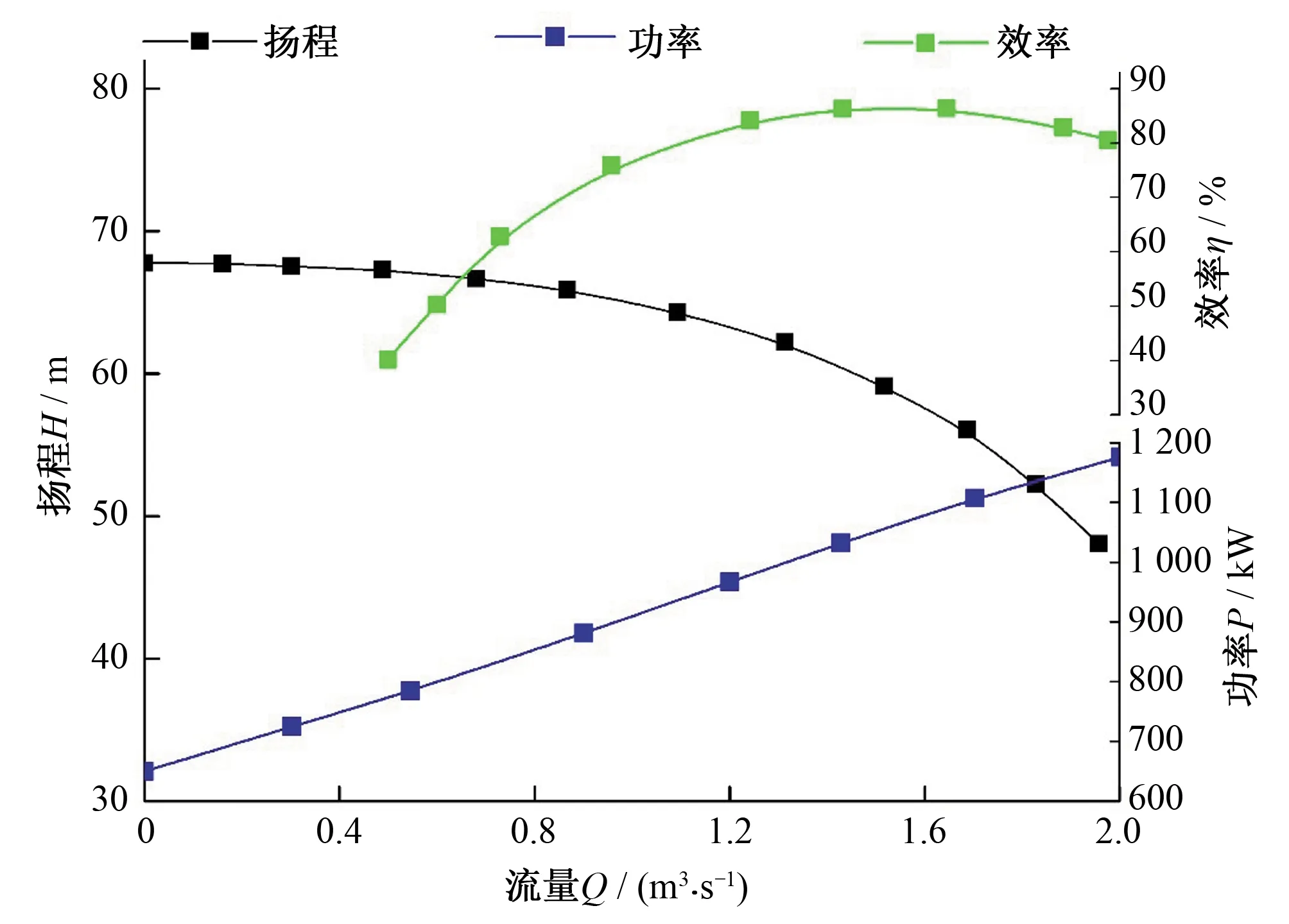
图5 N800-M9/1028T性能曲线

N500-M9/675：

H=-28.84Q2-10.74Q+74.643

(19)

η=-2.477Q2+2.691 7Q+0.148

(20)

P=220.92Q2+229.04Q+185.91

(21)

N700-M14/701T:

H=-15.456Q2+5.104 2Q+74.79

(22)

η=-0.547 5Q2+1.38Q+0.372

(23)

P=1.485 1Q2+36.655Q+585.33

(24)

N800-M9/1028T:

H=-7.575Q2+5.826 8Q+66.915

(25)

η=-0.437 2Q2+1.334 8Q-0.136 5

(26)

P=2.805Q2+262.56Q+645.76

(21)

当该多级泵站及泵站群在用水区需水流量为6.1 m3/s下运行时，总干二级的运行情况为：总流量为6.1 m3/s，净扬程为58.99 m，总扬程为60.8 m，3台N700-M14/701T在设计工况点运行，流量为1.1 m3/s；2台N800-M9/1028T，在设计点工况运行，流量为1.4 m3/s；而优化计算结果为：总流量5.8 m3/s，净扬程57.02 m，总扬程60.385 m，1台N500-M9/675，流量为0.54 m3/s，2台N700-M14/701T，流量为1.21 m3/s，2台N800-M9/1028T，流量为1.42 m3/s。两者相比，优化后的结果更好，流量5.8 m3/s可以满足用水区需求的流量5.78 m3/s，扬程也在限定范围内，且用水区需水流量为6.1 m3/s时，实际运行消耗4 528 kW，优化结果消耗3 686 kW，节约了842 kW，可减少18.6%的损耗，优化效果显著，泵站内机组可达到合理、高效的组合，可用于泵站的实际优化运行。

4 结 论

本文以某多级提水工程总干二泵站为研究对象，采用粒子群算法与动态规划法的混合算法对总干二级泵站进行系统的优化。对于站内而言，以总干二级为例，通过优化使其机组组合情况发生变化，模拟计算得到泵站的运行情况，当泵站总运行流量为6.1 m3/s时，其抽水流量为5.8 m3/s，扬程为57.02 m，有5台机组，3种不同型号的泵运行，优化后其单位运行时间内消耗3 686 kW，相对泵站实际运行情况节约了842 kW，节约了18.6%的能量。说明优化后的泵站在保证安全运行的前提下，得到了更优的调度方式，从而提高了泵站的运行效率，降低泵站整体运行的成本，节约能耗，最大程度地创造经济效益和社会效益。

□