玄武岩纤维加筋土的动本构特性试验研究

李胜男，骆亚生，严武庆，Samnang Phoak，尹 倩

(西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100)

0 引 言

土工加筋技术是指在土体中加入土工布等合成材料，利用其较强的延性来增加土体在动、静荷载下的强度参数和稳定性参数，以达到加固土体的目的[1-3]。与传统意义上的加筋土不同，纤维加筋土是指纤维丝与土料按固定配比充分搅拌形成的一类高级复合土料。由于土料内纤维的随机分布而形成立体结构，纤维加筋土体的性能参数有所增强[4]。众多专家学者对纤维加筋土的改善效果、作用原理及本构模型等方面进行了研究。高磊和刘芳[5,6]分别运用一系列三轴试验，研究了玄武岩和玻璃两种材质的纤维对土的加筋效果的影响。刘寒冰、Kirar等[7,8]分别研究了纤维的掺入对粉煤灰土和砂土的动力参数的影响。唐朝生等[9,10]基于一系列扫描电子显微镜试验结果，总结归纳了聚丙烯纤维加筋不同土料的纤维-土界面的微观机理。Sadeghi和 Beigi[11]通过试验与理论分析指出最优纤维含量是偏应力比的幂函数，并引入函数来描述循环荷载作用下的线性应力-应变关系。Li和Ding[12]以及Ghiassian[13]分别描述了纤维加筋土的非线性动本构模型。

综上可知，纤维在改良土体的动力参数方面具有明显作用，但有关玄武岩纤维加筋土动力特性方面的研究仍处于初步探索阶段[14]。本文基于室内动三轴设备提供的多组数据，分析纤维含量、含水率和围压对土体动应力-应变关系以及阻尼比和动弹性模量等动本构参数的影响。

1 试验材料和方法

1.1 试验材料

试验土料取自咸阳市杨凌区深度约5.5 m的某边坡。该土料的天然含水率为17.5%，天然干密度为1.38 g/cm3，其余指标见表1。

表1 试验土料的物理性质指标

试验材料采用玄武岩纤维，该纤维单位价格较低，力学参数和寿命参数更符合建筑要求[15]，基本理化参数见表2。

表2 玄武岩纤维的理化参数

1.2 试验方法

本文采用固结不排水动三轴试验方法，其数据来自双向土动三轴试验机。试验荷载采用级差为10 kPa的等效正弦荷载，初始动荷载幅值为10 kPa，振次为10，计取第五或第六组循环的试验参数，选取轴向动应变达到5%时作为破坏标准。对于同一条件下的试样，至少做3组重复试验，选取能代表大多数试验结果的一组数据进行分析。具体的试验方案如表3所示。

表3 试验方案

1.3 试样制备

本次试验所用试样的干密度均为1.65g/cm3，压实度达95%以上。为确保纤维在试样中的分布效果，需先将干燥的纤维丝与土料均匀混合后，再喷洒去离子水，封闭保存24h，再制作试样。试样为高8cm、半径3.95cm的圆柱体，采用图1所示的制样器通过从两端一次压样成型的方法制样，可以有效避免由分层制样法带来的不良影响，同时保证纤维的均匀分布。

图1 制样器

2 试验结果与分析

2.1 玄武岩纤维加筋土的动应力-应变关系曲线分析

图2～图4为玄武岩纤维加筋土和无筋土的代表性动应力-应变(σd-εd)函数曲线。曲线整体表现为应变硬化型，即随着动应变的发展，动应力在振动初期迅速增大，达到某一临界点后，增速明显减缓并稳定至一幅值。

2.1.1 围压对动应力-应变关系曲线的影响

由图2可见，无筋土和玄武岩纤维加筋土的动应力均与围压呈明显正相关。因为围压的存在使试样在受荷的过程中不易发生土体颗粒间的相互错动，限制了变形的发展。并且固结围压数值越大，土体颗粒-纤维界面的摩擦咬合效应越明显，摩阻力越大，表现为相同动应变水平下动应力的增大。

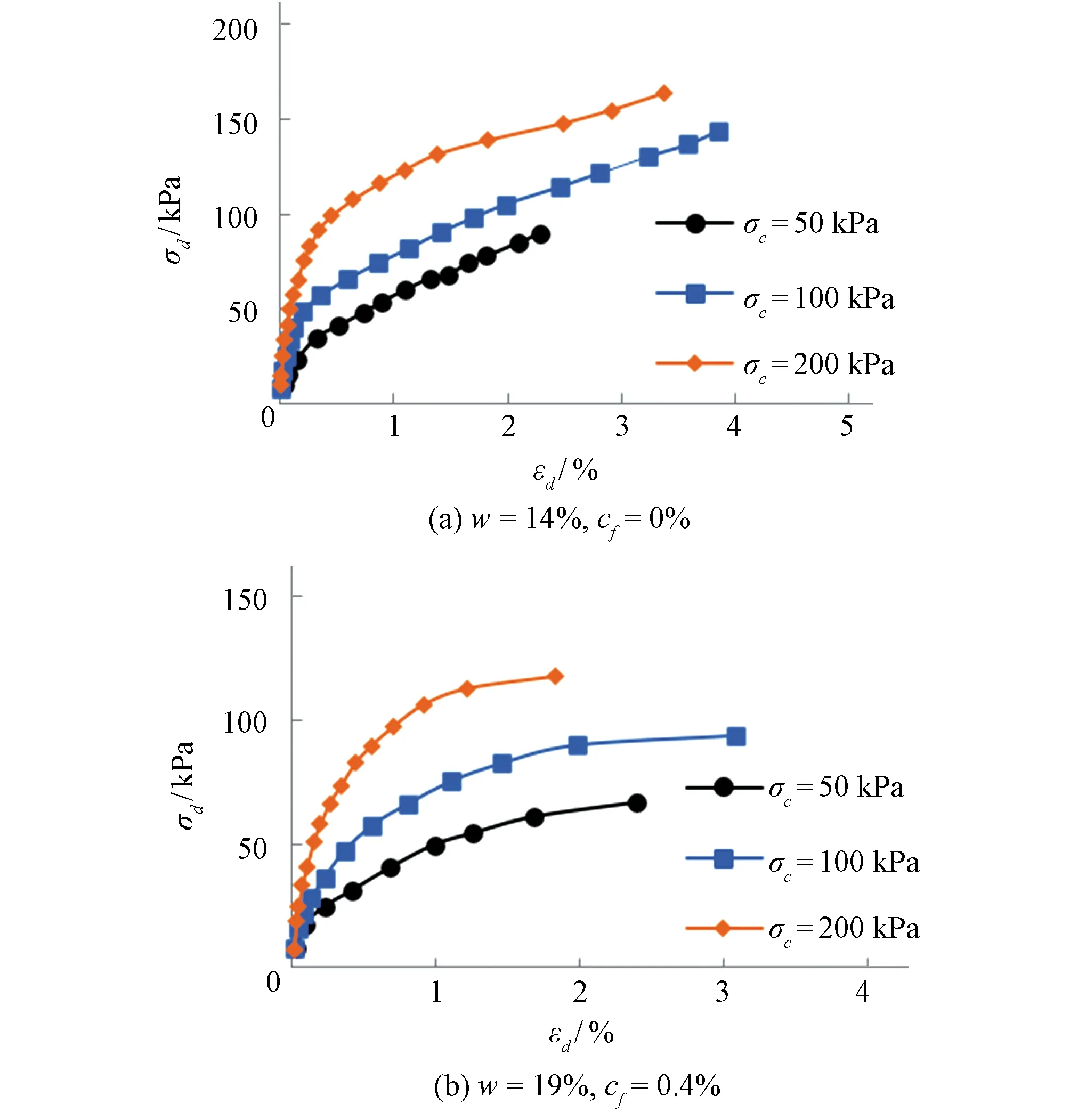
图2 不同围压条件下的σd-εd曲线

2.1.2 含水率对动应力-应变关系曲线的影响

由图3 可知，随着试样的湿度降低，土体颗粒与纤维细丝间的摩擦力和黏聚力增大，即动应变保持不变时动应力增大。

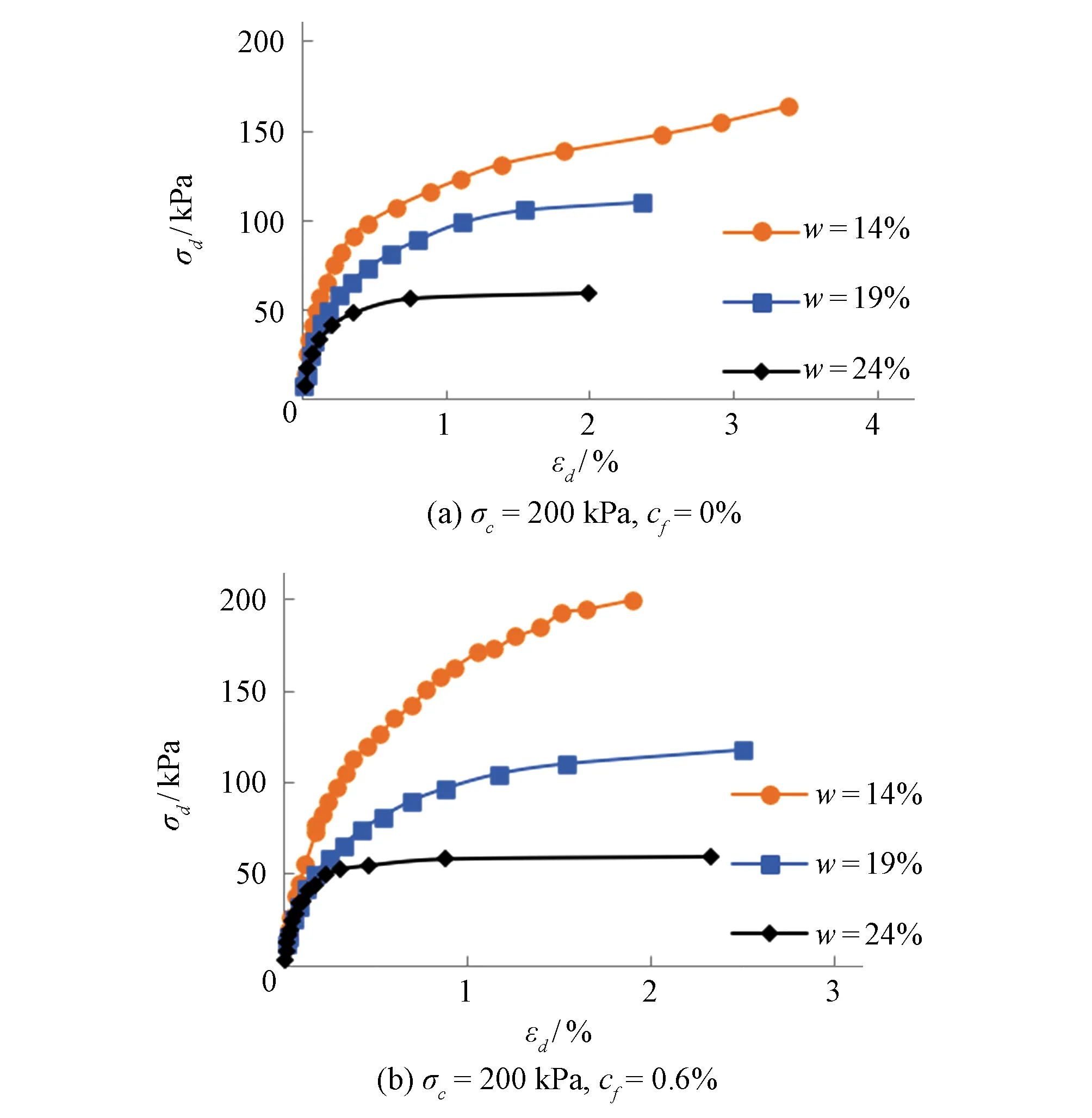
图3 不同含水率条件下的σd-εd曲线

2.1.3 纤维含量对动应力-应变关系曲线的影响

由图4可以看出，当动应变保持一致时，玄武岩纤维加筋土的动应力整体大于无筋土的动应力，但随着含水率和围压的变化，纤维含量相异的σd-εd曲线位置高低和疏密程度有较大差异。当含水率等于14%时，玄武岩纤维加筋土与无筋土在低围压的σd-εd曲线位置相对集中，玄武岩纤维无明显加筋作用；而高围压下玄武岩纤维的掺入发挥了显著的加筋作用，玄武岩纤维加筋土的σd-εd函数曲线明显位于无筋土的σd-εd函数曲线之上。但对于含水率较大的试样，随着围压由低升高，不同纤维含量对应的σd-εd曲线分布由疏变密，逐渐趋于同一化，表明动荷载作用下玄武岩纤维对土体的加筋效果在小围压条件下更为显著。

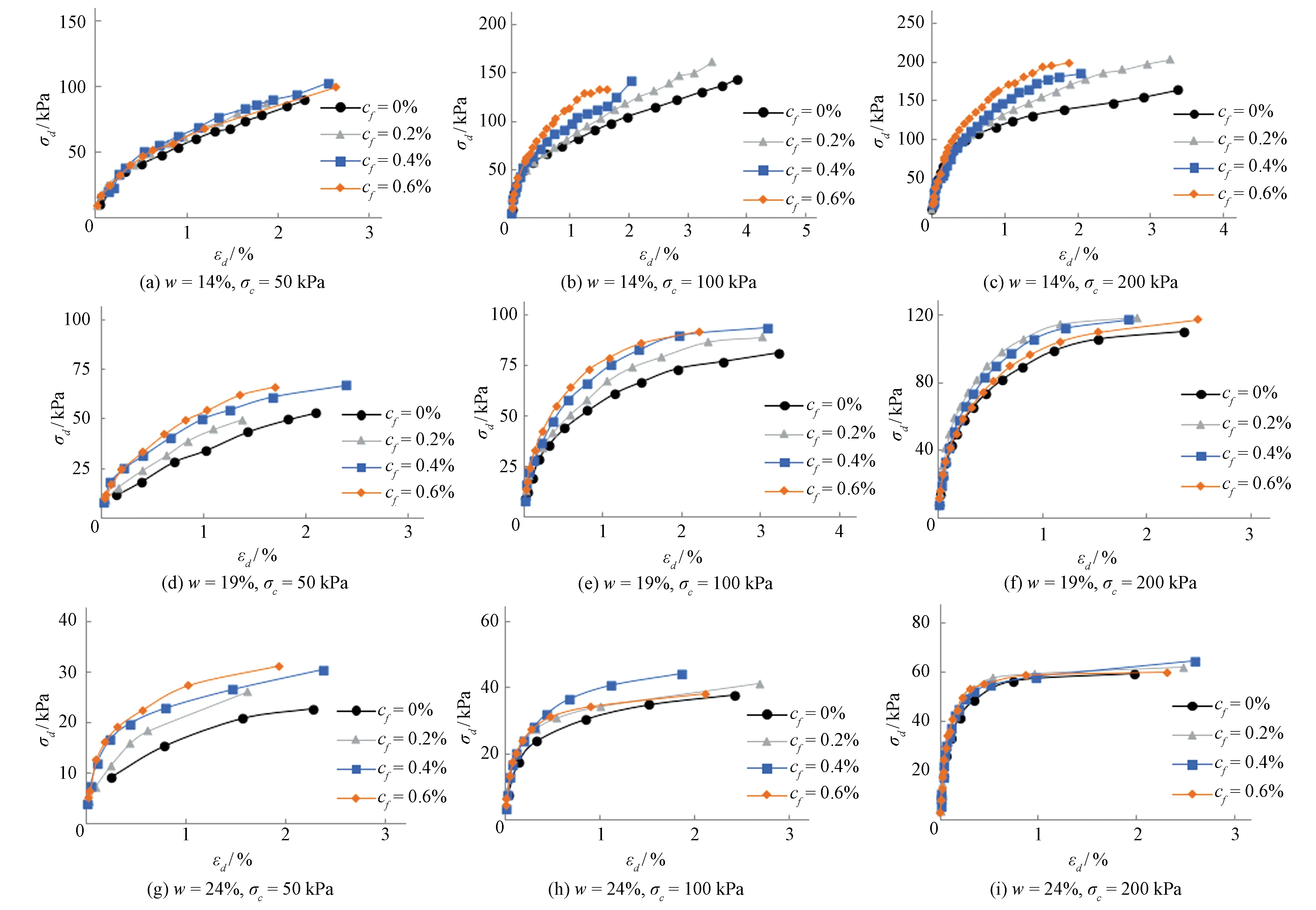
图4 不同纤维含量条件下的σd-εd曲线

纤维在土体内的加筋效应包括离散纤维的单向拉伸效应和网状纤维的立体拉伸效应[16, 17]。加筋的作用由纤维和土体颗粒之间的黏结力和摩擦力决定[9,10]。当试样含水少时，纤维-土体颗粒界面的结合水发挥主要作用。因此在较大围压条件下，玄武岩纤维-土体颗粒界面的摩擦及黏结作用较强，更利于纤维加筋效果的发挥。随着试样含水率的增加，界面黏结力的影响减弱，在竖向动荷载作用下，低围压条件下试样的变形(趋势)更为明显，一方面，因受力而变形的纤维网通过立体拉筋效应来分担外部荷载，另一方面，土体颗粒与纤维相对移动时产生了一定的摩阻力。因此较小的围压值更益于纤维对土体的加筋作用。

2.2 玄武岩纤维加筋土的动弹性模量分析

玄武岩纤维加筋土和无筋土的代表性动弹性模量-动应变(Ed-εd)函数曲线见图5～图7。振动前期，试样为近弹性状态。当塑性应变逐步发展，Ed-εd曲线急剧下降。在动应变到达临界点之后，塑性特性占据变形的主导地位，Ed-εd曲线趋于稳定。

2.2.1 围压对动弹模的影响

由图5可知，高围压条件不利于土体颗粒与纤维间的相对移动，限制了塑性应变的增大，表现为土体的动弹模和临界动应变的增加。

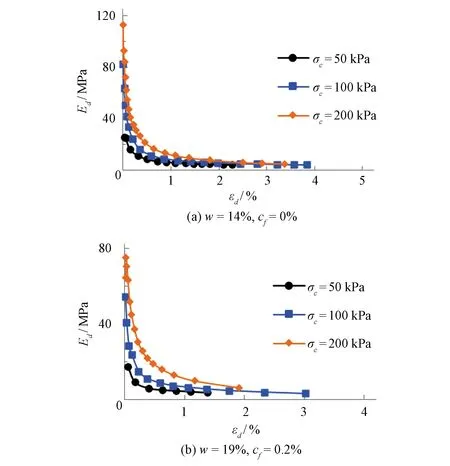
图5 不同围压条件下的Ed-εd曲线

2.2.2 含水率对动弹模的影响

根据图6，当含水率降低时，对应的动弹模增大，塑性应变发展减缓，对应的临界动应变值增大。

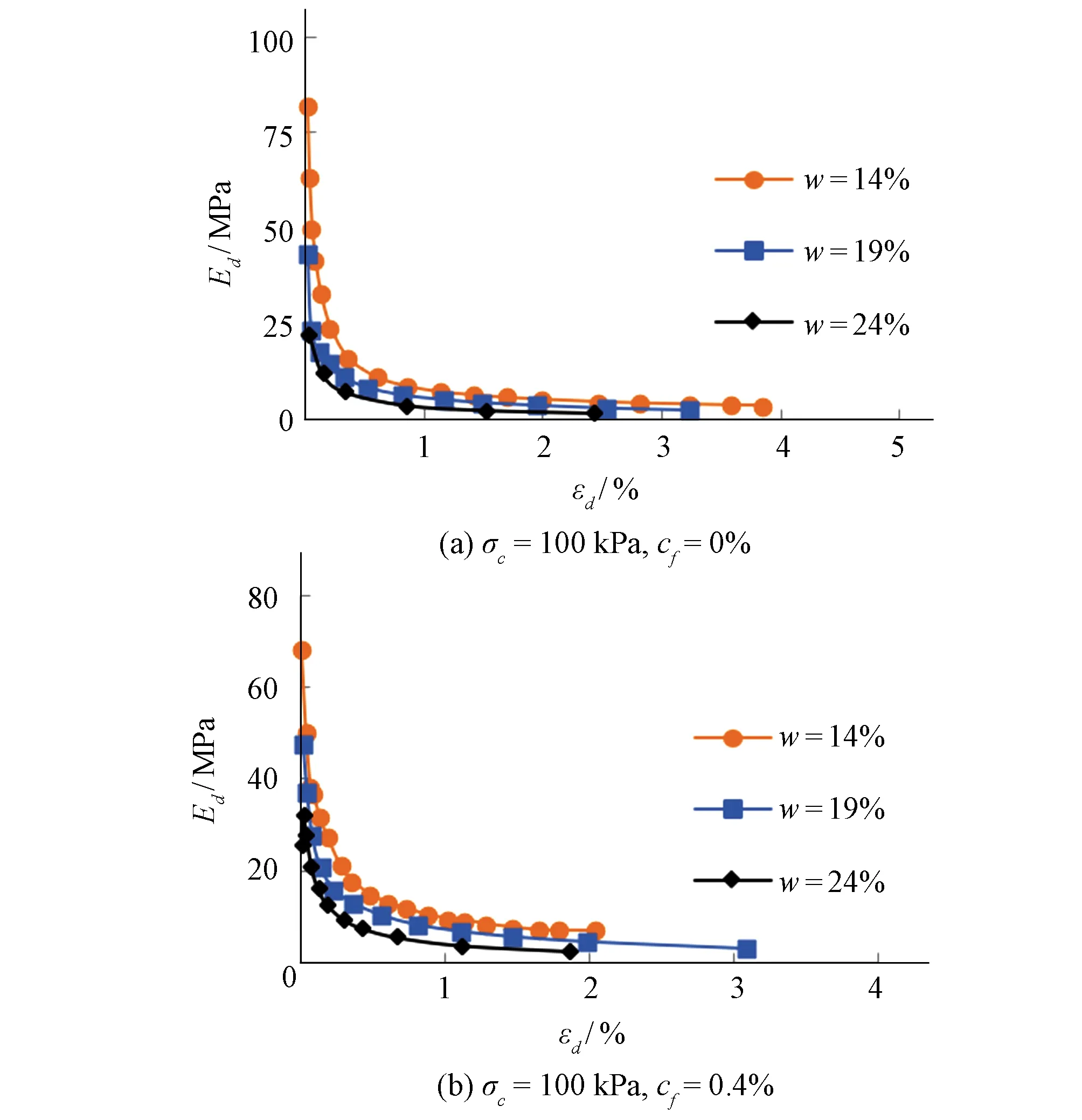
图6 不同含水率的土体的Ed-εd关系曲线

2.2.3 纤维含量对动弹模的影响

由图7可以看出，不同条件下玄武岩纤维加筋土和无筋土的Ed-εd函数曲线均无明显差别，表明动弹性模量与土体中掺入的玄武岩纤维含量无关。

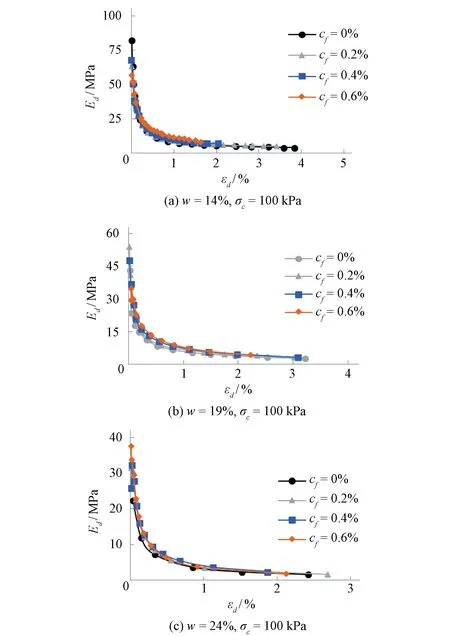
图7 不同纤维含量条件下的Ed-εd曲线

2.3 玄武岩纤维加筋土的阻尼比分析

阻尼比λ反映土体在周期荷载作用下能量内耗的特性[18]。本次试验的阻尼比绘制于图8、图9的λ-εd关系图中。当含水率较大时，阻尼比先与动应变呈正相关，后趋于稳定至最大值附近，最大阻尼比集中分布于0.10～0.24之间。

2.3.1 含水率对阻尼比影响

从图8中λ-εd函数曲线的分布位置可以看出，增加土体中的含水率能够起到增加阻尼比的作用。对比分析不同围压下的λ-εd函数曲线，当围压为200kPa时，将土体中的含水率由14%增大到19%，对应的阻尼比值显著增大，当将含水率进一步增大为24%时，土体的阻尼比基本不变。当围压为50kPa时，将土体中的含水率由14%逐步增大为24%，对应的阻尼比先基本不变后明显增大；100kPa围压下试样的阻尼比随含水率的增减情况介于以上两者之间。试验表明，对于不同围压条件下的玄武岩纤维加筋土试样，对应着各自的有效含水率区间。当含水率处于区间内时，该值的改变才会导致阻尼比的正相关变化，并且该区间的界限值与围压呈负相关[19]。因此，需要在考量围压等变量的前提下，分析比较含水率对玄武岩纤维加筋土阻尼比的作用。

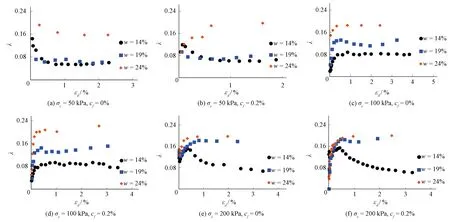
图8 不同含水率条件下的λ-εd曲线

2.3.2 纤维含量对阻尼比影响

根据图9，相比于无筋土，玄武岩纤维加筋土的阻尼比明显增大。当围压值变大时，纤维含量相异的土体阻尼比曲线渐进重合。表明试样内部随机分布的柔性纤维，在动荷载下可以增加试样的阻尼比，发挥减振效果。但围压值增大时，阻尼比受纤维影响的效果减弱。

2.4 玄武岩纤维加筋土动应力-应变关系的数学模型

国内外众多学者对土体的动本构参数进行了研究，H-D模型因形式简单、参数较少被广泛使用[20]。本文基于玄武岩纤维加筋土和无筋土σd-εd函数曲线的试验数据，对玄武岩纤维加筋土的σd-εd函数进行H-D模型拟合，并判断其适用性的优劣。H-D模型公式为：

(1)

以εd为横坐标，为εd/σd纵坐标，可以将上式中双曲线方程转换为直线方程：

(2)

式中：M、N为σd-εd函数曲线中初始动弹性模量的倒数和最大动应力的倒数。

由表4可知，由H-D模型拟合的相关系数全部大于90%，表明玄武岩纤维加筋土的动本构关系可以用H-D模型描述。掺入纤维后，土体的M、N值减小，并且当纤维含量相同时，试样的围压越大、含水率越小，通过拟合得到的M、N值越小。

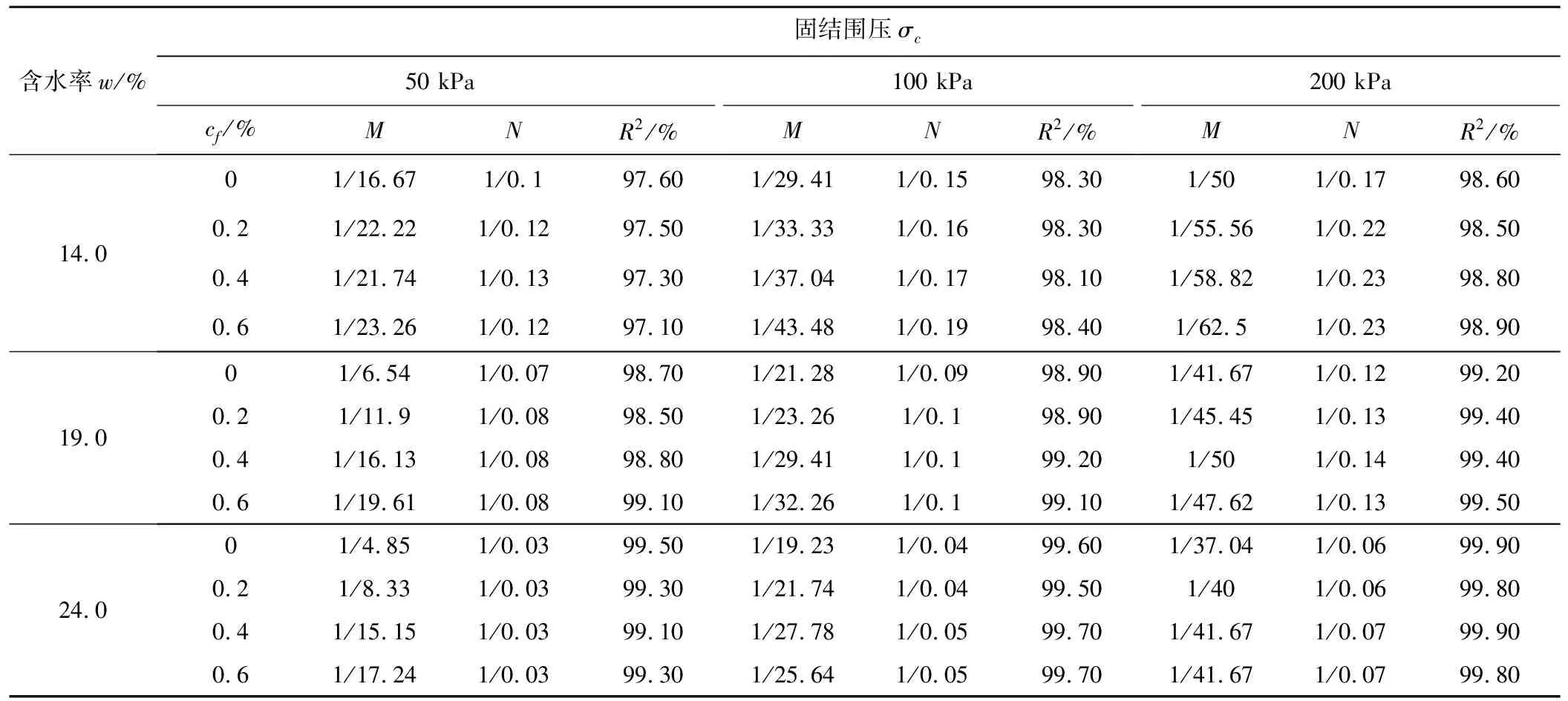
表4 土体的H-D模型参数

3 结 论

本文通过无筋土和玄武岩纤维加筋土的室内动三轴试验及数据分析，提出4点结论。

(1)玄武岩纤维加筋土的动应力-应变函数呈双曲线分布，符合H-D模型的拟合结果，模型参数值与含水率呈正相关，与围压呈负相关，同时受纤维含量的影响。

(2)当动应变保持固定数值时，混合纤维后土体的动应力明显增大，但不随纤维含量的增加而线性增大，含水率和围压的差异也会导致试验结果的不同：含水率较大时，围压值较小有利于纤维网减弱土体水平方向的形变量；含水率较大时，围压值较大有利于发挥纤维和土两种材料之间的黏合效果。三维纤维(网)受拉变形、纤维-土体颗粒界面的黏结作用和摩擦作用共同加强纤维对土体的加筋作用。

(3)玄武岩纤维加筋土和无筋土的动弹模与含水率呈负相关，与围压呈正相关，但不受纤维含量的影响。

(4)当围压作为自变量时，对应有不同的有效区间范围，含水率在该范围内的升降才能导致试样阻尼比的改变。在围压数值较小时，掺加玄武岩纤维可通过增加阻尼比，增强土体的减振性能。

因此，在研究动荷载作用下纤维对土体的动力特性的改善时，应综合考虑含水率、纤维含量、围压等多种因素。

□