斜交梁桥频率间接识别效果的影响参数

亓兴军 肖志全 张荣凤

摘 要：采用過桥车辆振动响应识别桥梁自振特性的间接测量法能够避免传统动载试验测量桥频方法存在的操作复杂和成本高等缺点。根据车桥耦合振动理论和桥梁间接测量法基本原理，对实际工程中的某一斜交梁桥建立车辆与桥梁耦合振动的有限元模型，采用双轴半车模型模拟测量车辆，提取车辆匀速驶过桥梁时的车辆加速度时程响应，并利用峰值拾取法进行频谱分析，剔除已知的车辆相关频率识别出桥梁的前三阶自振频率，分析了6种不同车速、6种不同车重、8种不同桥梁斜交角度对桥梁频率识别效果的影响特点。结果表明，间接测量法能够有效地识别桥梁比较密集的频率，车速低于20 km/h时，能够较好地识别出斜交梁桥的前3阶频率，车速较高时无法识别桥梁的频率信息;相对较小的车桥质量比对桥梁频率识别有利;斜交梁桥不同的斜交角度基本不影响桥梁频率识别的精度;桥面粗糙时采用差值法仍能较好地识别。数值模拟表明，间接测量法对于不规则斜交梁桥频率仍有较好的识别效果。

关键词：车桥耦合;斜交梁桥;间接测量法;粗糙桥面;自振频率

中图分类号：U441 文献标志码：A 文章编号：2096-6717（2020）06-0119-08

Abstract： An indirect measurement method is adopted to identify the bridges natural vibration characteristics by vibration response of vehicles crossing the bridge，it can avoid the disadvantages of the traditional method of measuring bridge frequency in dynamic load test， such as complicated operation and high cost. Based on the theory of vehicle-bridge coupling vibration and the basic principle of bridge indirect measurement method， the finite element model of vehicle-bridge coupling vibration is established for a skew beam bridge in practical engineering. A biaxial half-car model is used to measure the vehicle and extract the time-history response of the vehicle acceleration when the vehicle passes the bridge at a constant speed. Excluding known vehicle-related frequencies.The first three natural frequencies of the bridge are identified.The influence of six different vehicle speeds， six different vehicle weights and eight different bridge skew angles on the bridge frequency identification is analyzed. The results show that the indirect measurement method can effectively identify the frequency of bridges with high density. When the speed is less than 20 km/h， the third-order frequency of skew beam bridge can be well recognized. When the speed is high， the frequency information of the bridge cannot be recognized.The relatively small ratio of vehicle and bridge mass to bridge frequency identification is advantageous. The accuracy of frequency identification is not affected by the different angle of oblique beam bridge.When the bridge deck is rough， the method of acceleration subtraction can still be used for frequency identification. Numerical simulation shows that the indirect measurement method still has a good recognition effect for the irregular skew beam bridge frequency. To promote the application of motion sensing indirect measurement method in bridge inspection engineering.

Keywords：vehicle-bridge coupling; skew girder bridge; indirect method of measurement; rough bridge surface; natural vibration frequency

桥梁频率不仅是反映桥梁整体结构完整性的重要指标，也是桥梁动力特性的重要参数，对桥梁承载力的评估具有重要参考价值[1-2]。现行测量频率方法应用最多的是桥梁动载试验，通过在桥梁上安装多组加速度传感器，利用有线或无线采集系统记录桥梁的动力响应，该方法需要中断交通且繁琐费力[3]。

根据车桥耦合理论和间接测量法原理进行频率识别是一种有效的识别手段，车辆驶过桥梁时，车辆与桥梁相互作用和影响的问题为车桥耦合问题。其研究自1825年人类有了第一条铁路就已开始[4-5]，在20世纪60年代以前，主要集中在简单移动荷载作用下铁路桥梁的车桥耦合动力分析研究上，20世纪60年代以后，随着高等级公路桥梁的大量修建，公路桥梁的车桥耦合问题越来越吸引桥梁界科研人员的关注，并且随着计算机的出现和有限元软件的应用，使得建立复杂的车桥耦合振动模型成为可能。Yang等[6]首次提出基于动力测试间接测量桥梁频率的方法，用单自由度车模型模拟检测车辆，检测车辆通过桥梁时，其垂向的惯性力和弹簧力经车轮以接触力形式传递到桥梁造成桥梁结构的振动，由于耦合作用，桥梁振动将再次影响到检测车的垂向振动，并为其主要振动源。因此，只要分析检测车垂直方向的响应，即可得出桥梁特征参数信息，从而规避了车桥耦合时变系统有载频率变化的限制[7]。其主要贡献是利用单轴四分之一车辆通过某一简支梁桥推导出了解析解，该公式结果与Yang等[8]提出的利用车辆与桥梁耦合单元计算出的数值解吻合，理论验证了车辆竖向加速度解析解中包含了桥梁频率的基本信息。Lin等[9]通过现场试验验证了该方法的有效性，说明了间接测量法识别桥梁频率的可行性。在此基础上，陈上有等[10]用车轮加弹簧阻尼器簧上质量模拟移动小车，根据车辆的加速度响应的频谱分析，成功地识别出简支梁桥的一阶频率;王希等[11]进行了在桥梁平整状态下由车辆振动信息识别简支梁桥固有频率的研究，可以准确识别桥梁的第一阶基频;Malekjafarian等[12]利用列车不同车厢的振动信息识别出了简支梁桥的基频; Kong等[13]利用单自由度小车识别出某简支梁桥的前三阶频率;Yang等[14]在桥梁间接测量法的回顾文章中阐明了间接测量法应用的注意事项以及单自由度车辆模型的局限性。

前人的研究多集中于利用简支梁桥和单自由度车辆模型进行数值模拟分析，且主要是桥梁基频的识别。笔者选用更加贴近实际的双轴半车车辆平面模型，并选用实际工程中的三跨斜交梁桥建模，运用间接测量理论识别出了桥梁的前3阶频率。在20世纪60年代以前，车桥耦合多是现场试验研究，总结出经验公式或理论来指导桥梁设计;60年代以后，车桥动力相互作用的研究方法多采用试验与理论相结合的方法，即用试验的方法校核理论的正确性，用校核过的、正确的理论方法进行车桥耦合振动的仿真分析，研究结构各参数对振动的影响。笔者主要运用后者方法，基于车桥耦合理论与间接测量法原理，通过有限元数值模拟方法得到理论解与试验数值，其基本流程：1）利用Ansys有限元软件建立桥梁模型，通过模态分析模块得到桥梁前3阶频率的理论解;2）建立车桥耦合模型，利用Ansys有限元软件的瞬态动力分析模块，模拟车辆驶过桥梁的过程，通过采用不同的参数得到车体的加速度时程后利用峰值拾取法等手段得到识别频率;3）将这两步得到的频率进行误差对比和验证分析。桥梁间接测量法不同于传统的桥梁频率测量方法，将加速度传感器放置于测试车辆上，不用在桥上架设各种仪器，且桥上任意移动车辆对频率识别无不利影响[15]，因此具有较大的应用前景。

1 理论依据

依据间接测量法理论[6]，单轴四分之一测量车辆模型匀速驶过等截面简支梁桥，量测车质量为mv、刚度为kv、车辆移动速度为v。桥梁总长度为L，单位长度质量为m-，截面抗弯刚度为EI，车桥振动简图如图1所示，桥梁因车辆作用导致振动产生坐标x处挠度为u（x）。

2 模型参数

运用ANSYS中的瞬态动力学分析方法进行车桥耦合振动数值模拟计算分析[16]，利用耦合命令约束车轮与相关桥面点的竖向位移，编制APDL车桥耦合振动命令流计算车辆和桥梁的动态响应，然后利用车辆响应识别出桥梁前3阶自振频率。

2.1 桥梁建模

工程实例为跨径组合为28 m+45 m+28 m的混凝土连续梁桥，斜交角为30°，桥面宽度为8 m，上部结构为单箱单室主梁。全桥主梁采用C50预应力混凝土，弹性模量为EC=3.45×104 MPa，为模拟桥梁的倾斜支承边界条件，桥梁中横梁和端横梁均模拟为刚性横梁。桥梁横截面如图2所示。

3 不同工况下桥梁频率识别效果

基于车桥耦合理论建立车桥耦合有限元模型进行数值模拟分析，由于高阶桥梁频率对车辆动力响应贡献较小，间接测量法的识别效果较差[18]，现对桥梁只进行前3阶桥梁频率识别并进行相应的识别精度误差分析。

3.1 不同车速对频率识别效果的影响

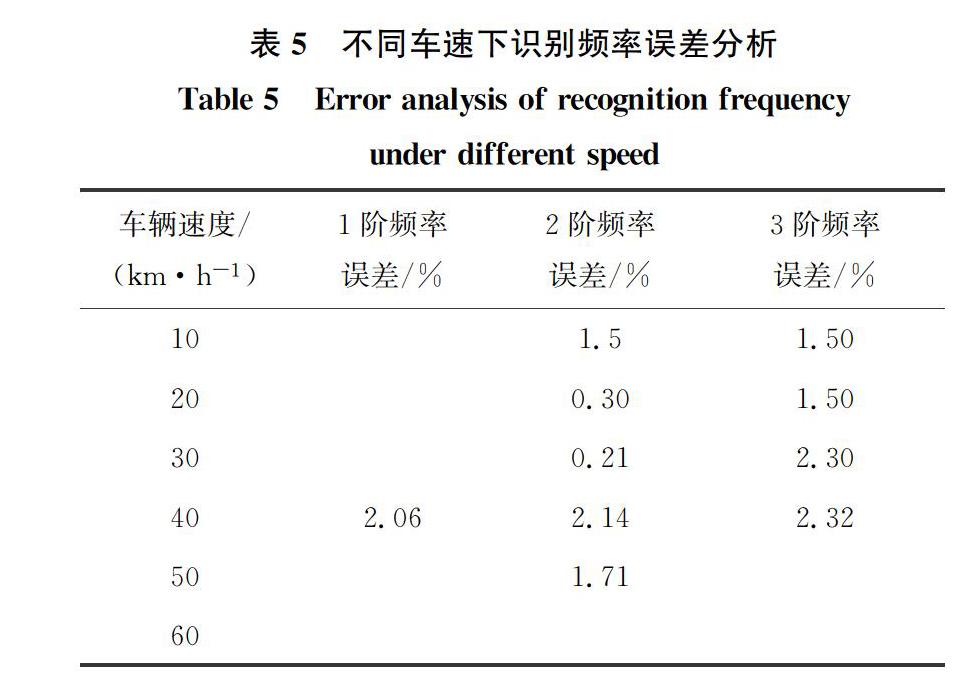
车辆匀速驶过该3跨连续斜交梁桥，选取6个不同车速，分别是10、20、30、40、50、60 km/h。在车辆质量为4 t的条件下计算得到车辆加速度时程数据，然后进行快速傅里叶变换得到频谱图，识别结果的频谱如图5所示，识别得到的桥梁频率数值如表4所示，识别频率与理论计算频率的相对误差如表5所示。

通过表5误差分析可得，速度对桥梁基频识别结果基本无影响，对高阶识别较不利。速度在20 km/h及以下时，识别精度较高，高车速时无法有效识别桥梁的频率信息。

3.2 不同车桥质量比对频率识别效果的影响

为了分析不同的车桥质量比mv/（m-L）对桥梁频率识别精度的影响，在10 km/h的车速下，选取不同的车桥质量比进行频率识别，结果如图6所示。

从图6中可以看出，每条车辆加速度频谱曲线都有6个峰值，它们分别是车辆转动频率1.67 Hz，10 km/h时驱车频率2πv/L为0.08 Hz，车辆竖向振动频率ωv因车辆质量不相等而数值不同，车辆竖向频率随着车重增加而逐渐减少，这3个频率信息可以通过事先测试车辆而已知，并且數值相对于桥梁频率一般较小，所以可以较明显地区分出后面3个峰值为桥梁的前3阶频率信息。观察上述加速度时程数据频谱图，可以轻松地排除已知的驱车频率、车辆转动频率和车辆竖向频率，最后识别出桥梁前3阶频率信息。

从表6和表7可以看出，随着车桥质量比的增大，其识别出的频率值和识别频率误差基本无变化，仍能较好识别出桥梁的前3阶频率。通过图6看出，随着车桥质量比的增大，识别出的桥梁频率峰值逐渐不明显，变得难以辨识。因此，为了获得较好的识别效果，建议选用小的车桥质量比。

3.3 不同斜交角度对频率识别效果的影响

改变桥梁的斜交角度，分析间接测量法提取桥梁频率的识别效果，选取8个不同的桥梁斜交角度，角度分别是0°、10°、20°、30°、40°、50°、60°、70°。在车重为4 t、车速为10 km/h的条件下进行车桥耦合振动计算得到车辆加速度时程数据，然后进行快速傅里叶变换，得到车辆加速度频谱图，识别结果如图7所示。

从表8中可以看出，斜交桥不同的斜交角度会对桥梁的刚度产生影响，随着斜交角度的增大，基频增高。

从图7和表9中可以看出，间接测量法对所有不同斜交角度桥梁的识别效果均较好，与理论频率的最大误差不超过4%，均满足工程精度要求。相对而言，斜交角度在70°以下时识别精度较好，对于斜交角度在50°时，2阶桥频和3阶桥频由于太过接近而混为一簇大峰，使得2阶和3阶桥频峰值识别困难，仔细辨别后仍能从频谱图中识别出桥梁频率相关峰值信息;斜交角度在70°以上时，由于斜边支撑线与桥梁轴线接近平行，识别效果变差。但斜交角度在70°以上的桥梁在实际工程中几乎不存在，因此，可以认为斜交角度对桥梁频率的间接识别精度几乎没有影响。

4 桥面粗糙条件下频率识别

桥面不平整度是在实际应用中无法避免的一个重要影响因素。Chang等[19]提出了使用两个单自由度车模型匀速通过粗糙桥面，然后对得到的两个加速度时程曲线分别进行快速傅里叶变换，将得到的两个频谱图相减，以达到消除桥面不平整度对间接测量法的影响。Elhattab等[20]提出可以使用两个单自由度车模型匀速通过粗糙桥面，得到前后两车在过桥时段的加速度时程，然后选取它们在桥面同一位置时的加速度数值相减，使用加速度差值曲线进行桥梁模态参数识别，进而消除桥面不平整度对识别结果的影响，笔者采用后者方法进行频率识别。桥面不平整度参照《车辆振动输入与桥面平度表示方法》（GB/T 7031—1986）模拟，采用简谐波叠加法（三角级数法），生成101 m长桥面C级不平整度，如图8所示。

从图9中可以看出，单辆车无法识别粗糙桥梁的频率，两车差值方法可以准确识别出粗糙桥梁的前3阶频率，1阶频率识别误差为0.41%;2阶频率识别误差为1.30%;3阶频率识别误差为2.12%。可以看出C级桥面粗糙条件下差值法能够较好地解决粗糙度对桥梁频率识别的干扰。

5 结论

车速低于20 km/h时能够较好地识别出斜交梁桥的前3阶频率，车速较高时无法识别桥梁的频率信息;相对较小的车桥质量比对桥梁频率识别有利;斜交梁桥不同的斜交角度基本不影响桥梁频率识别的精度，桥面粗糙条件下采用差值法仍能较好地识别桥频。数值模拟表明，间接测量法对于不规则斜交梁桥频率仍有较好的识别效果，可进一步推进移动传感间接测量方法在桥梁检测工程中的应用。

本方法的优点是省时省力、不中断交通;缺点是用弹簧来模拟非线性的车辆减振系统可能仍不够精确;现场试验时的有色噪声也是重要的干扰因素，因此，在工程中的应用还需要进一步的实桥试验研究。 参考文献：

[1] R.克拉夫， J. 彭津. 结构动力学[M]. 北京： 高等教育出版社， 2006.

CLOUGH R， PENZIEN J. Dynamics of structures[M]. Beijing： Higher Education Press， 2006. （in Chinese）

[2] 夏禾， 張楠. 车辆与结构动力相互作用[M]. 北京： 科学出版社， 2005.

XIA H， ZHANG N. Dynamic interaction of vehicles and structures[M]. Beijing： Science Press， 2005. （in Chinese）

[3] 李焕兰. 简支梁桥损伤状态下车桥耦合动态响应分析[D]. 辽宁 大连： 大连海事大学， 2015.

LI H L.Dynamic response analysis of vehicle-bridge coupling under damaged state of simply supported girder bridge [D]. Dalian， Liaoning： Dalian Maritime University， 2015.（in Chinese）

[4] BIGGS J. Introduction to structural dynamics[M]. New York： Mc Graw-Hill Book Co， Inc， 1964.

[5] FRBA L. Vibration of solids and structures under moving loads[M]. Dordrecht： Springer Netherlands， 1972.

[6] YANG Y B， LIN C W， YAU J D. Extracting bridge frequencies from the dynamic response of a passing vehicle [J]. Journal of Sound and Vibration， 2004， 272（3/4/5）： 471-493.

[7] 杨永斌.非传统思维的桥梁监测法[J].桥梁， 2015，66 （4）：34-36.

YANG Y B. Bridge non-traditional monitoring method [J]. Bridge， 2015， 66（4）： 34-36. （in Chinese）

[8] YANG Y B， YAU J D. Vehicle-bridge interaction element for dynamic analysis [J]. Journal of Structural Engineering， 1997， 123（11）： 1512-1518.

[9] LIN C W， YANG Y B. Use of a passing vehicle to scan the fundamental bridge frequencies：An experimental verification [J]. Engineering Structures， 2005， 27（13）： 1865-1878.

[10] 陈上有， 夏禾. 从过桥车辆响应中识别桥梁结构基本自振频率的方法[J]. 工程力学， 2009， 26（8）： 88-94.

CHEN S Y， XIA H. An identification method for fundamental frequency of bridge from dynamic responses due to passing vehicle [J]. Engineering Mechanics， 2009， 26（8）： 88-94. （in Chinese）

[11] 王希. 由车辆响应识别桥梁固有频率的方法研究[D]. 长沙： 中南大学， 2009.

WANG X.Identification of natural frequencies of bridges by vehicle response [D]. Changsha： Central South University， 2009. （in Chinese）

[12] MALEKJAFARIAN A， OBRIEN E J. Identification of bridge mode shapes using short time frequency domain decomposition of the responses measured in a passing vehicle [J]. Engineering Structures， 2014， 81： 386-397.

[13] KONG X， CAI C S， DENG L， et al. Using dynamic responses of moving vehicles to extract bridge modal properties of a field bridge [J]. Journal of Bridge Engineering， 2017， 22（6）： 04017018.

[14] YANG Y B， YANG J P. State-of-the-art review on modal identification and damage detection of bridges by moving test vehicles [J]. International Journal of Structural Stability and Dynamics， 2018， 18（2）： 1850025.

[15] 杨晓天. 桥面不平整下连续梁桥频率的间接识别[D]. 济南： 山东建筑大学， 2019.

YANG X T. Frequency identification of continuous bridge based on indirect method considering the unevendeck [D]. Jinan： Shandong Jianzhu University， 2019.（in Chinese）

[16] 刘世忠. 双层公路钢桁梁桥车桥耦合振动研究[D]. 西安： 长安大学， 2015.

LIU S Z.Study on vehicle-bridge coupling vibration of double-deck highway steel truss bridge [D]. Xian： Changan University， 2015. （in Chinese）

[17] 谢天宇. 桥梁动态讯息间接测量法的多种工况分析研究[D]. 重庆： 重庆大学， 2017.

XIE T Y. A study on the working conditions analysis for the bridge indirect measurement method [D]. Chongqing： Chongqing University， 2017.（in Chinese）

[18] YANG Y B， LIN C W. Vehicle-bridge interaction dynamics and potential applications [J]. Journal of Sound and Vibration， 2005， 284（1/2）： 205-226.

[19] CHANG K C， WU F B， YANG Y B. Effect of road surface roughness on indirect approach for measuring bridge frequencies from a passing vehicle [J]. Interaction and Multiscale Mechanics， 2010， 3（4）： 299-308.

[20] ELHATTAB A. Drive-by bridge damage monitoring： concise review [J]. Civil Engineering Research Journal， 2017， 1（1）： 25-29. DOI：10.19080/cerj.2017.01.555555.

（編辑 胡玲）