基于实测值的Landsat 8水面温度反演算法对比
——以太湖为例
陈 争, 王 伟,2*, 张 圳,3, 王 怡,4
(1.南京信息工程大学应用气象学院, 南京 210044; 2.南京信息工程大学气象灾害预报预警与评估协同创新中心/江苏省农业气象重点实验室, 南京 210044; 3.南京信息工程大学无锡研究院, 无锡 214105; 4.南京信息工程大学滨江学院, 无锡 214105)
水面温度直接或间接地影响着湖泊的物理、化学、生物和生态过程[1]。首先,水面温度是决定湖泊与大气之间感热和潜热交换的关键参数[2]。在物质传输方程中,水面温度既是计算感热通量的直接因子,也通过水面饱和水汽压影响潜热通量[3],进而调节能量再分配[4-5]。其次,作为湖泊水温垂直分布的初始值,水面温度通过改变水体热力层结和垂直混合来影响深水区的溶解氧浓度[6]。再次,水面温度通过改变水体温度对水生动植物的数量和分布产生影响[7-8]。如世界第二大淡水湖泊——坦噶尼喀湖的水体层结随水面温度升高而增强,水体垂直混合减弱,深层养分上涌减少,使湖泊初级生产力下降了20%,鱼类产量下降了30%[9]。此外,水面温度会影响湖泊甲烷排放量和蓝藻爆发频率[10-11]。试验表明,水温较高阶段的甲烷排放量约为水温较低阶段的5.2倍[12]。据估计,到21世纪末,因水温升高,北方湖泊甲烷释放量将增加20%~54%[13],湖泊蓝藻爆发频率将增加20%[14]。可见,要深入研究湖泊的物理、化学、生物和生态过程,必须获取湖泊水面温度信息。
观测湖泊水温的方法主要有原位观测和遥感反演。原位观测分两种:定点、高频的连续观测(如锚定浮标)和走航、低频的定期巡测(如船载走航),两种方法均存在采样点少、空间覆盖范围小的缺点[15],且观测的大多是表层水温(如20 cm深处水温)而非水面温度[16]。与原位观测相比,遥感技术可以拓展水面温度观测的空间尺度。MODIS(moderate resolution imaging spectroradiometer)1999年至今、AVHRR(advanced very high resolution radiometer)1979年至今和TM/ETM+/TIRS(thematic mapper/enhanced thematic mapper plus/ thermal infrared sensor)1982年至今等传感器获取的热红外数据被广泛用于水面温度反演[17],其中,2013年2月11日成功发射的Landsat 8卫星为遥感反演水面温度提供了新的数据选择。与TM和ETM+数据相比,Landsat 8的热红外传感器TIRS有两个热红外波段[18],不仅可以更好地消除大气对反演结果的影响[19],且适用于劈窗算法反演表面温度。相较于AVHRR(空间分辨率为1.1 km)和MODIS(空间分辨率为1 km),TIRS数据的空间分辨率更高,为100 m。可见,Landsat 8的热红外遥感数据在水面温度反演方面更具优势。
利用观测数据验证反演结果是Landsat 8反演水面温度的关键环节,现有研究多使用表层水温[20-21]或MODIS地表温度产品[22-24]而非水面温度来验证Landsat 8反演结果。然而,湖泊表面有一层几毫米厚的薄层,除了风扰动或热力不稳定引起的表层水体对流混合外,水体与大气之间的辐射和能量交换会造成表层水温与水面温度存在差异[25],该差异在夏季弱风和强日照时尤为明显[26],达到1.5 K[27-28]。MODIS地表温度产品被广泛用于地表热力特征研究[29-30],其表面温度空间格局虽与实测值接近,但反演的绝对数值与实测值依然存在一定差异[31],该差异在湖泊甚至超过2 K[32-33]。与表层水温和MODIS地表温度产品相比,基于红外辐射原理观测的水面温度是更理想的验证数据。该观测包括两种:辐射传感器(如CNR4,Kipp & Zonen B.V)和红外测温传感器(如SI-411,Apogee Instruments Inc.)。两种传感器均基于Stefan-Boltzmann定律观测表面温度,都考虑了下垫面比辐射率对表面温度的影响,观测精度均优于0.2 K[34],且两者之间的相关性超过0.94[35]。除上述共同点外,两种传感器之间存在以下两点差异。首先,辐射传感器的视角(如CNR4为180°)大于红外测温传感器(如SI-411为44°)。其次,辐射传感器必须水平安装,其观测面积是半径为10倍观测高度的圆面[36]。红外测温传感器通常倾斜于地表安装,其观测面积为椭圆,且椭圆面积随倾斜角度增加而增大[37]。安装高度相同时,辐射传感器观测值代表的面积大于红外测温传感器。
目前,利用Landsat 8反演太湖水面温度取得了一定的成果[20, 38],但以下两个方面尚需深入研究。首先,当前研究多选择单景[39]或冬春两季[20]的Landsat 8影像来反演太湖水面温度,缺乏在四季对反演算法的对比。其次,当前研究都采用太湖表层水温作为验证数据,缺乏用实测水面温度验证Landsat 8反演结果的研究,湖面多点验证的研究尤为缺乏。作者所在团队建立的太湖中尺度通量网是全球首个湖泊多站点联网观测网络[40],太湖多点(5个站点)、连续(2010年6月至今)和高分辨率(1 Hz)的水面温度观测为开展以上两点研究提供了可能。现基于实测水面温度数据,量化太湖表层水温与水面温度之间的差异,对比分析利用Landsat 8热红外数据反演太湖水面温度的4种算法,以期为表面温度最优反演算法的选择和太湖生态系统保护提供科学参考。
1 研究区域与数据介绍
1.1 研究区域
太湖位于长江三角洲,水域面积为2 400 km2,平均水深为1.9 m,水深小于1.5 m的水域主要分布在沿岸地区及东太湖湖区,水深大于2 m的水域主要在西太湖,最大水深(2.6 m)出现在西太湖平台山西部及北部[41]。太湖年平均气温为16.5 ℃,年总降水量1 176 mm[42]。太湖周边经济发达,城市化程度高[43],导致生态环境恶化,水体污染和富营养化日益严重[44]。西部湖区上游流域工农业发达,入湖污染物通量最高,水华持续时间可长达11月[45]。
1.2 数据介绍
Landsat 8卫星上装载了两个传感器:OLI(operational land imager)陆地成像仪和TIRS热红外传感器,共11个波段,其中band 10和band 11为反演表面温度所用的两个热红外波段。选取四景四季典型日期的晴朗少云(云量<10%)且覆盖太湖水域的Landsat 8影像为数据源,过境日期分别为2014年7月22日(夏)、2014年10月26日(秋)、2014年 12月 29日(冬)和2018年4月28日(春),过境时刻为北京时间10:31。

图1 太湖中尺度通量网和湖上观测平台
所用的小气候、水温梯度和辐射四分量观测数据来自于太湖中尺度通量网的5个湖面站点(图1):避风港站(BFG)、大浦口站(DPK)、梅梁湾站(MLW)、平台山站(PTS)和小雷山站(XLS)[40]。小气候观测系统由温湿度传感器(型号HMP155A,Vaisala Inc.)和风速风向传感器(型号05103, R. M. Young Company)构成,用于计算反演算法中的部分参数。水温观测(型号109-L, Campbell Scientific Inc.)分为水下20、50、100、150 cm 4个梯度,底泥温度用相同的温度传感器观测。四源净辐射表(型号CNR4,Kipp & Zonen B.V.)用于测量向下短波辐射、向上短波辐射、向下长波辐射和向上长波辐射。
基于向下长波辐射L↓和向上长波辐射L↑观测数据,通过Stefan-Boltzmann定律计算湖面温度Ts[46],以验证反演结果,该方法被广泛应用于计算水面温度[4, 47-48],即
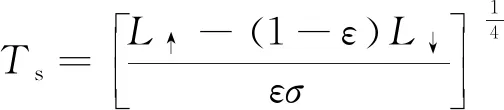
(1)
式(1)中:ε为水面比辐射率,取0.97;σ为Stefan-Boltzmann常数,为5.669 6×10-8W/(m2·K4)。
从观测设备维护和数据交叉验证两个方面保证了水面温度观测数据的可靠性。首先,每月对5个站点的四源净辐射表进行1次镜头擦拭和水平校准,每年将生产商校准过的同款仪器安装在5个站点平行观测10 d,对比结果显示辐射表的测量偏差小于1.0 W/m2。其次,对比BFG站建站初期(2011年12月—2012年12月)的水面温度红外观测数据(型号SI-411,Apogee Instruments Inc.)和由式(1)计算的水面温度发现,两者之间的相关系数和一致性系数均超过0.99,均方根误差为1.31 K,平均绝对误差为0.10 K。
2 水面温度反演算法
选取了4种算法:辐射传输方程法(RTE算法)[49]、覃志豪单窗算法(MW算法)[50]、Offer Rozenstein劈窗算法(SW1算法)[51]和Jiménez-Muoz劈窗算法(SW2算法)[52]进行太湖水面温度反演算法对比研究。
2.1 辐射传输方程法
辐射传输方程法的基本原理是去除热辐射总量中大气对地表热辐射的影响,进而得到地表热辐射强度,再将地表热辐射强度转化为相应的地表温度[49]。由于视域外杂散光的影响,Landsat 8的band 11定标偏差大于band 10,根据美国地质勘探局建议[53],单波段反演算法均使用band 10。RTE算法具体计算公式为
Lλ=[εB(Ts)+(1-ε)L↓]τ+L↑
(2)
式(2)中:Lλ为热辐亮度;ε为地表比辐射率;B(Ts)为黑体热辐射亮度;τ为大气透过率。温度为Ts的黑体在热红外波段的辐射亮度B(Ts)为
B(Ts)=[Lλ-L↑-τ(1-ε)L↓]/τε
(3)
Ts由普朗克函数计算为

(4)
对于Landsat 8热红外数据,常数K1和K2分别为774.89 W/(m2·μm·sr)和1 321.08 K。辐射传输方程法需要的大气剖面参数由NASA(National Aeronautics and Space Administration)官网提供的计算方法获得。
2.2 覃志豪单窗算法
单窗算法是覃志豪等[50]以地表热辐射传输方程为基础,利用Landsat TM/ETM+band 6反演地表温度的算法,将其参数调整后用于Landsat 8热红外数据的水面温度反演。计算公式为
Ts={a(1-C-D)+[b(1-C-D)+
C+D]Tλ-DTa}/C
(5)
C=ετ
(6)
D=(1-τ)[1+(1-ε)τ]
(7)
式中:C和D为中间变量;Tλ为卫星传感器所探测到的像元亮度温度;a和b为回归系数;Ta为大气平均作用温度。获取星上辐亮度(Li)后,利用普朗克函数计算星上亮度温度,即
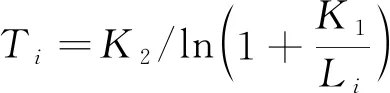
(8)
式(8)中:Ti为band 10或band 11的像元亮度温度;K1和K2为卫星发射前预设常量,数值同式(4)。
式(5)中,不同温度范围内a和b数值参考文献[50],不同大气模式下的大气平均作用温度Ta取值参考文献[54],大气透过率τ是大气水汽含量ω的函数,ω的计算方法详见文献[55-56]。
2.3 Offer Rozenstein劈窗算法
Rozenstein等[51]依据劈窗算法,结合Landsat 8数据的特点,提出了适用于Landsat 8数据的地表温度反演劈窗算法SW1:
Ts=A0+A1T10-A2T11
(9)
式(9)中:T10、T11分别为Landsat 8 band 10、band 11的亮度温度,K;A0、A1和A2的计算公式为
A0=a10E1-a11E2
(10)
A1=1+A+b10E1
(11)
A2=A+b11E2
(12)
E1=D11(1-C10-D10)/E0
(13)
E2=D10(1-C11-D11)/E0
(14)
A=D10/E0
(15)
E0=D11C10-D10C11
(16)
式中:Ci、Di的计算公式如下(i=10,11),其余系数计算方法和取值同前。
Ci=εiτi
(17)
Di=(1-τi)[1+(1-εi)]τi
(18)
2.4 Jiménez-Muoz劈窗算法
Ts=T10+C1(T10-T11)+C2(T10-T11)2+C0+(C3+C4ω)(1-ε)+(C5+C6ω)Δε
(19)
Δε=ε10-ε11
(20)
式中:系数C0~C6为模拟实验得到的系数,依此取-0.268、1.378、0.183、54.30、2.238、-129.20、16.40。
选取相关系数R、Willmott一致性系数I、均方根误差(root mean square error, RMSE)和平均绝对误差(mean absolute error, MAE)定量评价4种算法对太湖水面温度的反演效果。统计参数的计算方法如下。n为样本数量,TsO和TsR分别代表水面温度观测值和反演值,上横线表示平均值。

(21)
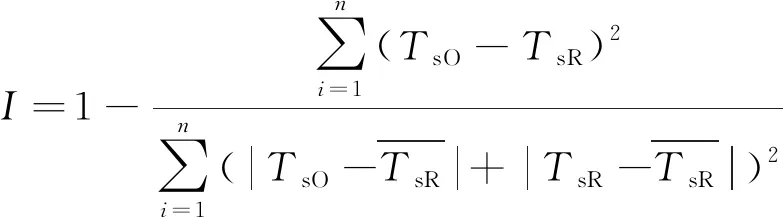
(22)
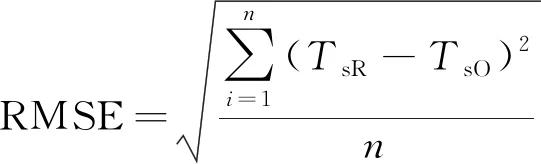
(23)
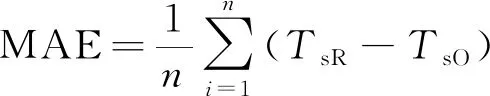
(24)
3 结果分析
3.1 太湖水面温度与表层水温的对比
基于实测数据量化了水面温度与表层水温之间的差异。如图2所示,春夏秋冬四季Landsat 8过境日期的太湖水面温度Ts、水下20 cm温度T20cm和水下50 cm温度T50cm呈现相似的单峰型日变化特征。从0:00—7:30水温变化微弱,日出之后水温先上升后下降。Ts、T20cm和T50cm的峰值和谷值分别出现在午后和日出前后。随着深度增加,温度峰值和谷值出现时间推后,如2014年12月29日的Ts、T20cm、T50cm达到谷值的时间分别为7:00、8:00、8:30,达到峰值的时间分别为14:00、15:00、15:30。与Ts相比,T20cm和T50cm达到峰谷值的时间分别推后了1、1.5 h。分层次来看,与T20cm和T50cm相比,Ts的日变化幅度最大,这与热量交换主要发生在水气界面有关。
4个日期的水温在大多数时间里均表现为Ts>T20cm>T50cm,白天尤为明显,最大温差出现在15:30前后。4个日期Ts与T20cm最大温差分别为3.6、1.6、2.9、3.0 K,Ts与T50 cm最大温差分别为5.6、2.2、3.3、3.4 K。由此可见,表层水温与水面温度存在显著差异,且该差异随着水深增加而变大。太湖水体水温出现垂直温差主要与太阳辐射和风速有关。白天,太阳辐射随着水深增加而衰减,水体各层所吸收的辐射能从上至下逐渐减少,形成了水体的热力分层,在晴朗、高温、小风的午后尤为明显[27]。风速影响水体上下层混合和热量传递,风速增加,垂直混合增强,垂直方向水温梯度减小。2014年7月22日的Ts与T20cm、T50 cm的差值较小与该日风速较大有关。
在Landsat 8过境时刻,均呈现为Ts>T20cm>T50 cm。如表1所示,2018年4月28日过境时刻,T20cm、T50cm分别比Ts低2.5、2.9 K;2014年7月22日过境时刻,T20cm、T50cm分别比Ts低1.3、1.5 K;2014年10月26日过境时刻,T20cm、T50cm分别比Ts低2.7、2.8 K;2014年12月29日过境时刻,T20cm、T50cm分别比Ts低2.2、2.3 K。

表1 Landsat 8在太湖过境时刻Ts与T20 cm、T50 cm的差值
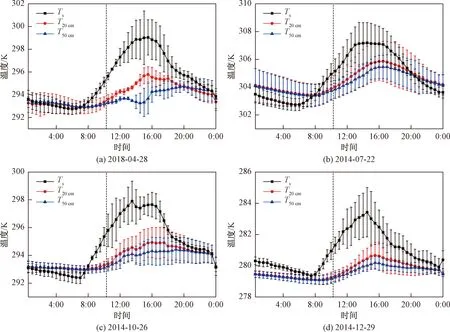
误差线代表5个站点的标准差,垂直虚线表示Landsat 8在太湖过境时刻

图3 4种算法反演值与太湖水面温度实测值之间的线性拟合关系
选取的4种常用水面温度遥感反演算法理论成熟。其中,RTE算法需要在NASA官网输入卫星过境时研究区的位置、时间以及气象等信息,依据这些信息计算Landsat 8 band 10的大气上行辐射、大气下行辐射和大气透过率等参数,这些参数是基于实时大气廓线模拟得到,理论上反演误差小于1.0 K[57]。模拟试验表明,利用MW算法反演地表温度时误差可以控制在1.1 K以内,SW1和SW2算法的理论精度在0.4~0.8 K[58]。由此可见,不同表面温度的遥感反演算法误差均小于Landsat 8过境时太湖水面温度与表层水温的差值,这意味着当分别用Ts、T20cm、T50cm验证遥感反演结果时,得到的太湖水面温度最优反演算法不同。为了保证结果准确性,将用实测数据计算的Ts验证太湖水面温度的Landsat 8反演结果,以评价RTE、MW、SW1和SW2 4种地表温度反演算法在太湖的适用性。
3.2 4种算法反演太湖水面温度空间分布的性能对比
对4种算法反演得到的太湖水面温度与实测水面温度进行了线性回归分析。如图3所示,4种算法对太湖水面温度的反演值与实际值的相关系数和一致性系数均达到0.99,其中,SW2算法反演结果的RMSE(1.4 K)和MAE(0.3 K)最小,SW1算法反演结果的RMSE(2.2 K)和MAE(1.3 K)最大。具体而言,RTE算法在冬季的反演值与实测值的差异小于0.3 K,夏季的反演值比实测值低3.0 K。MW算法的反演值相对于实测值系统偏小1.0~2.0 K。SW1算法和SW2算法在冬季时的反演值偏低,其中SW1偏低2.0~3.0 K,SW2偏低0.3~1.0 K,两者在夏季时的反演值较实测值偏高,其中SW1偏高2.0~3.0 K,SW2偏高0.1~1.4 K。综合拟合方程和统计参数来看,SW2算法的反演结果与实测值最为接近,反演精度最高,MW和RTE算法次之,SW1算法反演结果与实测值偏离最远,反演精度最低。图3对比分析中包含了太湖水面温度的时间变化(4个日期)和空间变化(5个站点)信息,下文将通过求4 d平均和站点平均分别从空间和时间两个角度来评价4种反演算法在太湖的适用性。
表2列出了4种算法在不同站点的4 d平均反演温度与实测温度的对比。如表2所示,RTE算法和MW算法在5个站点的水面温度反演值与实际值的绝对误差范围为0.2~2.7 K,其中在BFG站和XLS站的反演误差较大。SW1算法在5个站点的反演温度与实测温度的绝对误差最大,分别是3.0、2.2、1.4、1.0、-0.4 K,RMSE和MAE分别为1.8、1.4 K。SW2算法的反演温度与实际温度的绝对误差最小,分别是2.0、1.2、0.4、0.1、-1.4 K,RMSE为1.3 K,MAE小于1.0 K。总体而言,在空间尺度上,4种算法的水面温度反演值与实测值的绝对误差小于3.0 K、RMSE小于1.8 K,与宋挺等[20]研究结果相近。然而,反演结果无法体现太湖水面温度的空间梯度。统计宋挺等[20]的表5、表6数据发现,与本文研究结果类似,其水面温度反演值与表层水温观测值的相关系数也出现负值。使用的水汽含量和大气平均作用温度均为5个观测站点的平均值,平滑了一部分太湖水面温度的空间分布信息,即使使用MODIS水汽产品来估算反演所需的水汽含量[20],依然难以体现太湖水面温度的空间格局,这可能与太湖湖面较为均一、温度梯度小有关[32]。
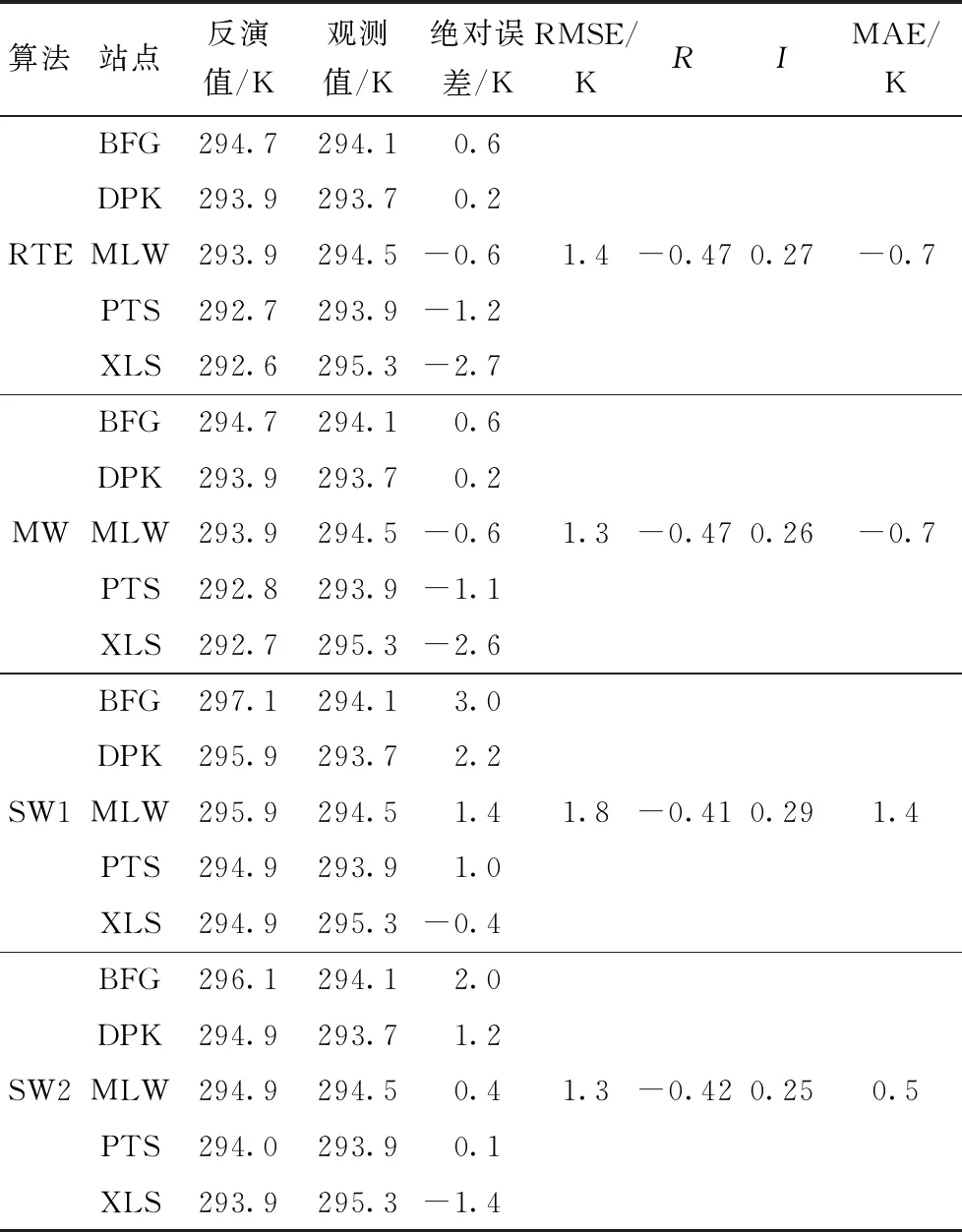
表2 4种算法在5个站点的水面温度反演值与实测值的对比
3.3 4种算法反演太湖水面温度时间变化的性能对比
表3列出了4种算法在4个日期的5个站点平均的水面温度反演值与实测值的对比。如表3所示,4种算法在四季代表日期的反演值与观测值之间的相关系数和一致性系数均达到了0.99。RTE和MW算法在2018年4月28日、2014年7月22日、2014年10月26日和2014年12月29日的反演温度与实测温度的绝对误差为0.3~1.3 K。SW1算法的反演温度与实测温度的绝对误差在四季间波动最大,夏季最高(3.2 K),冬季最低(-0.1 K)。SW2算法在4个不同日期的反演温度与实测温度的绝对误差均相对较小,分别为-0.1、1.0、0.3、-0.1 K。并且,SW1算法的RMSE和MAE最大(1.8、1.2 K),RTE和MW算法的RMSE和MAE接近1.0 K,SW2算法的RMSE和MAE最小(0.5、0.3 K)。综合来看,在时间尺度上,SW2算法对太湖水面温度的反演效果最佳,RTE和MW算法次之,SW1算法最差。

表3 4种算法在4个日期的水面温度反演值与实测值的对比
4 讨论
经上述分析可知,在时间和空间尺度上,SW2算法对太湖水面温度反演的效果最佳,其次是MW和RTE算法,SW1算法反演效果最差。单波段算法(如RTE算法)的经验关系在水汽浓度高的条件下很不稳定,导致夏季RTE算法反演误差偏大[59]。相较RTE算法,MW算法引入了大气平均作用温度Ta以提高地表温度反演精度,可以降低在水汽含量较高情况下的反演误差,但Ta是基于标准大气的温度和湿度廓线资料,根据地表温度推算而得,存在计算误差[50]。SW1算法对水汽含量较敏感,水汽含量变化1 g/cm2,SW1算法的反演结果变化0.4 K,这可能是导致SW1算法在夏季反演误差最大(3.2 K)的主因。SW2算法对水汽含量敏感性较低,水汽含量变化1 g/cm2,其地表温度反演结果仅变化0.1 K[20],这也是SW2算法反演误差最小的主因。
宋挺等[20]基于两景Landsat 8数据对太湖冬春两季水面温度进行反演研究,验证数据是水下40 cm处的水温值,其结果显示MW、SW1和SW2算法在MLW、DPK和PTS绝对误差范围分别为0.4~2.2 K、0.6~1.4 K和0.3~1.2 K,略高于本文的反演误差(< 0.5 K)。阚增辉等[39]基于太湖春季的两景Landsat 8影像,利用RTE、SW2算法反演了太湖地区地表温度,并利用中国气象科学数据网提供的地表温度插值得到过境时刻数值验证了反演结果。当地物类型为水体时,SW2算法反演结果比RTE算法高0.93 K,本研究发现春季SW2算法比RTE算法反演结果高0.9 K。可见,不同的验证数据会影响反演算法精度的定量评估,有必要在湖面利用辐射传感器或红外测温传感器开展水面温度观测,以验证水面温度的遥感反演结果。
5 结论
基于太湖中尺度通量网的观测数据,量化了太湖表层水温与水面温度的差异,基于四季4个典型日期的Landsat 8热红外数据,利用辐射传输方程法(RTE)、覃志豪单窗算法(MW)、Offer Rozenstein劈窗算法(SW1)和Jiménez-Muoz劈窗算法(SW2)反演了太湖水面温度,并基于实测值在时间和空间尺度上对4种反演算法进行了评价。得到的结论总结如下:
(1)太湖水下20 cm水温T20cm、水下50 cm水温T50cm与实际水面温度Ts均呈现午后高、夜晚低的单峰型日变化特征,白天Ts分别比T20cm和T50cm高3.6、5.6 K,Landsat 8过境时刻Ts分别比T20cm和T50cm高2.7、2.9 K。不能利用表层水温代替水面温度验证Landsat 8的反演结果。
(2)与太湖实测值相比,SW2算法对太湖水面温度的反演效果最佳,MW和RTE算法次之,SW1算法反演效果最差。其中,RTE算法在温度较低时的反演值接近于实际值,温度较高时反演值比实测值偏低1.0~3.0 K。MW算法反演值比实测值系统偏低1.0~2.0 K。SW1算法在温度低/高时的反演值较实测值偏低/高2.0~3.0 K。无论高温还是低温,SW2算法的反演误差均处于0.1~1.4 K。
(3)4种算法反演的水面温度与观测值之间的相关系数和一致性系数均达到0.99,均能反映太湖水面温度的时间变化特征,但难以量化其空间格局。

