一种用于彩色图像分割的GA-K-Means方法

李 勇， 赵 杰

(1.核工业西南物理研究院, 成都 610041； 2.成都理工大学工程技术学院, 乐山 614007)

图像分割技术主要是根据原始图像的灰度、颜色、纹理等信息将不同的区域分开,并将人们感兴趣的部分提取出来,如在医疗技术、智能采摘、自然灾害勘察等领域就需要较高精度的图像分割结果[1]。典型的图像分割方法有边缘分割、阈值分割、区域分割、均值聚类分割等[2],彩色图像包含的信息量多于灰度图像,但是彩色图像还是由不同灰度级的3个R、G、B分量构成,因此其分割方法也是源于灰度图像分割方法。

相关学者提出的改进型图像分割方法主要有：根据彩色图像3个相互独立的H、S、I分量特点及其直方图确定K均值(K-Means)聚类的类别和初始聚类中心点,分别在高、低饱和度区聚类[3],分割精度较高,但是算法中的卷积运算量较大；利用图像信息构造拟合项,自定义适应权值函数为局部项和全局项赋权值,由此模型分割多种灰度不均图像[4],该方法没有考虑彩色图像的情况；通过计算像素的非局部空间信息提高抗噪能力与分割精度,通过“投票模型”自适应生成犹豫度作为抑制因子修正隶属度,提高算法的运行效率[5]；通过统计果实的外形特征数据并建立几何模型,以标记的质心作为模型的中心,在变换后的二值图像中重新建立几何模型,利用其边界拟合出分割线[6],其分割结果相当于二值化(果实与背景)；将边缘检测与改进的全局K均值相结合的模糊C均值聚类(fuzzyC-means clustering，FCM)算法,克服了迭代次数多、收敛速度慢、运算量大的缺点[7]；将彩色图像R、G、B分量的灰度矩阵转换成清晰度矩阵,最后在Lab彩色空间通过K均值聚类法进行图像分割[8]；把RGB三色空间转换到均匀的Lab空间,再分解得到特征分量,最后利用K均值聚类法分割[9],该方法耗时较短,但聚类中心数目固定,不易得到最佳聚类结果。

由于彩色图像包含了较丰富的色彩、亮度等信息,其分割不限于简单的灰度级处理,本文分析了典型K均值聚类算法与FCM算法的特点,提出一种基于遗传算法(GA)的K均值聚类方法(GA-K-Means)进行彩色图像分割,该方法的特点是：聚类中心数目不是固定的唯一值,而是将其与聚类中心点共同构成染色体的基因进行择优搜索,其中的择优标准(适应度函数)为图像的彩色特征相似度(feature similarity of color，FSIMC)。最后对18幅不同类型的彩色图像进行分割实验,其仿真结果表明，采用GA-K-Means分割方法分割的18幅图像具有较高的FSIMC,迭代运算的收敛性较好。

1 K-Means聚类与FCM分割方法

(1)典型的K-Means聚类分割法[2]为：根据事先设定的聚类中心数目K,将具有相同属性(如灰度或颜色等)的像素划分为不同的K个区域,其具体方法是通过式(1)计算各个簇点到K个聚类中心的欧氏距离E，即

(1)

式(1)中：xij为第i类第j个样本；Ni为第i类的样本个数；ci为第i类的聚类中心；k为聚类中心数目。将欧氏距离最小的簇点又按照式(2)重新计算新的聚类中心Ci，即

(2)

再计算欧氏距离,如此反复迭代,直到每个簇类不再产生新的聚类中心,即式(3)成立之时,则聚类过程结束。

Ci+1=Ci

(3)

K-Means聚类算法需要选取1个固定的聚类中心数目k,然后按照最小欧氏距离将图像分割为k类。聚类中心数目和聚类中心点的选取只能根据先验知识进行设定,如果这2个参量选取不当,则容易导致聚类结果陷入局部最优解,直接影响图像分割的精度[10]。

(2)模糊C均值聚类算法(FCM)与K-Means聚类法类似,不同之处在于：FCM算法的各个样本所属的类不再是非此即彼(要么是0要么是1),而是采用区间[0,1]中的概率表示各个样本隶属于某个类的程度(即所谓的隶属度),但是每个样本对各个类的隶属度之和必须为1[7，11]。

2 GA-K-Means分割方法

考虑到GA算法的全局搜索能力[12],将GA算法与K-Means聚类算法相结合,把每条染色体分为2部分(聚类中心数目和聚类中心点),以步进和GA算子相结合的方式搜索最佳聚类中心个数和聚类中心。基于GA-K-Means的图像分割流程如图1所示。

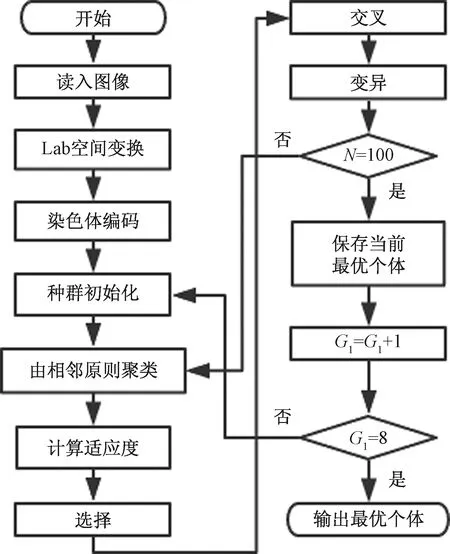
图1 GA-K-Means算法流程(300×365)

根据图1的GA-K-Means算法流程详细阐述彩色图像分割的具体步骤如下。

(1)读入彩色图像,生成R、G、B的三维矩阵向量,可认为对应3个灰度矩阵,灰度范围为0 ～ 255,由于RGB颜色空间的3个分量是高度线性相关的,在处理彩色图像的时候,一般将其按式(4)变换到XYZ过渡空间,再按照式(5)～式(7)变换到Lab颜色空间[10]。

(4)

L=100[f(Y/Yn)]-16

(5)

a=400[f(X/Xn)-f(Y/Yn)]

(6)

b=190[f(Y/Yn)-f(Z/Zn)]

(7)

式中：Xn、Yn、Zn是当式(4)中的R=G=B=100时所对应的X、Y、Z,即分别为94.9、99.9、108.8,而f(t)为

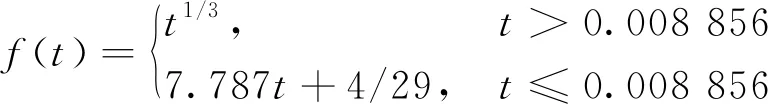
(8)

由式(5)～式(7)看出，Lab空间不同的分量取值范围不是完全相同的,可分别乘以不同的系数,使得各分量取值范围一致,分割完以后再逆向运算。

(2)染色体编码：每条染色体的基因G由2部分组成,即

G=G1∪G2

(9)

式(9)中：G1为聚类中心数目,设定G1的取值范围是2～7的整数,故采用3位二进制编码,由于取值范围较小,故该基因不采用遗传算子进行交叉、变异等操作,而是按步进值1进行递增；基因G2由G1个子基因gn(n=1,2,…，G1)串联而成,gn代表各个聚类中心点,其构成形式为{Labxy}。L、a、b代表颜色分量灰度,x、y代表像素坐标。为了提高处理速度与编码的一致性,将{Labxy}的每个值整定为[0,255]区间的整型数值,这样可采用与G1类似的二进制编码形式。由于G1在2～7取6个数值,那么需要编写6组不同长度的染色体,每组的染色体个数为40个,并且预先设定G1=2,同时设定遗传算子的交叉概率Pc=0.3,变异概率Pm=0.1,迭代次数N=100。

(3)种群初始化：当每次G1步进加1时,根据G1的值在第(G1-1)组染色体里面选取20个作为初始种群,即种群规模M=20。

(4)根据相邻原则聚类：以染色体的G1个聚类中心点为中心聚集邻近的像素点,先要把染色体的基因G2单独提取出来,然后按照式(10)聚类，即

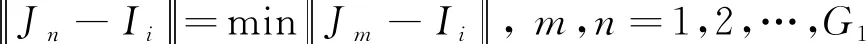
(10)

满足此条件的像素点Ii就属于第n个聚类中心,实际上这一步已经完成了图像的预分割。

(5)适应度值计算：在步骤(4)中只是根据相邻原则进行了图像的预分割,并没有按照式(1)计算传统K-Means聚类算法的三维欧氏距离,将FSIMC作为适应度函数值,FSIMC表示图像之间的相似性,其计算方法[13]为

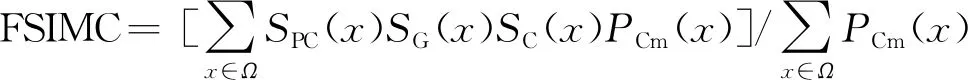
(11)

式(11)中：SPC(x)、SG(x)、SC(x)分别代表两幅图像的相位一致相似性、梯度相似性、色度相似性,PCm(x)代表相位一致性特征的最大值。

(6)选择、交叉、变异：根据步骤(5)中计算的适应度,将染色体进行高低排序,择优选择8个优秀染色体进入下一代,将其G2基因部分与同组其他染色体的G2基因部分按照设定的交叉概率和变异概率进行交叉、变异,产生新的种群,如果迭代次数没有达到100次,则返回步骤(4)重新聚类；反之,则提取当前最优的1条染色体与对应的FSIMC进行保存。

(7)将聚类中心数目G1按步进值1进行递增,若G1不等于8,则返回步骤(3)重新选取另外1组染色体进行聚类分割；反之,说明遗传算法已经筛选出6个最优染色体,则根据对应的6个FSIMC取最优的1条染色体输出,该条最优染色体的基因G1就是最佳聚类中心数目。

3 彩色图像分割实验

仿真实验采用的软件为MATLAB R2014,计算机CPU为Intel Core i5 CPU@3. 3 GHz,内存为8 GB,操作系统为Windows 7(64位)。选取6幅不同类型的图片(来源于千图网)进行裁剪,其格式均为*.bmp。

将这6幅图片分别采用K-Means聚类分割法、GA-K-Means分割法、FCM分割法进行分割,其结果如图2、图3所示。从这3种分割方法的分割效果来看,每幅图片的主体部分没有什么差别,但是在细节上可以分辨差异：例如大佛像的远景部分、菊花的花蕊部分、小鸡的眼睛和嘴巴阴影部分、山水的白云部分等细节在视觉上均具有明显差别。

使用的遗传算子在分割6幅图像时,迭代运算相应的收敛曲线如图4所示，其收敛代数均没有超过70代。

采用3种分割方法分割出来的图像对应的彩色特征相似度FSIMC、分割时间如表1所示,可以看出，提出的GA-K-Means方法分割出来的图像对应的FSIMC趋近于理论最大值1,相应的比其他2种分割方法的FSIMC值高10%左右。

为了进一步验证分割效果,下面再对另外12幅图像(来源于千图网)分成4组进行分割实验,拟说明本文所提方法的普遍有效性。

从图5～图8的分割结果来看,这12幅图片按照3种分割法得到的图像,其主体部分没有差别,主要的差异点在于细节部分的纹路和不同亮度部分的过渡，如图5中向日葵花盘四周花蕊的明暗过渡、图6中楼房墙壁上的影子轮廓、图7中古建筑右上角的远景部分、图8中海礁的海水明暗过渡等细节在视觉上均具有明显差别。3种分割法对应图像的FSIMC、分割时间如表2、表3所示。

图2 第1组图像分割结果 (753×563)

图3 第2组图像分割结果 (744×575)

图4 遗传算子的收敛曲线 (652×486)

表1 第1、2组图像的分割效果比较

图5 第3组图像分割结果 (730×538)

图6 第4组图像分割结果(737×514)

图7 第5组图像分割结果(728×558)

图8 第6组图像分割结果(727×543)

表2 第3、4组图像的分割效果比较

表3 第5、6组图像的分割效果比较

从表2、表3可以看出，按照本文GA-K-Means方法分割出来的图像,其FSIMC比K-Means聚类分割法、FCM分割法分割出来的图像对应的FSIMC值高10%左右。GA-K-Means分割法得到的最大FSIMC为0.912,趋近于理论最大值1,其分割时间相应地比其他2种分割方法消耗的时间略长。

4 结论

提出的GA-K-Means彩色图像分割方法可以使分割后的图像具有较好的特征相似度,能够把最佳的聚类中心数目筛选出来。对于多幅像素大小不一、色彩内容复杂度差别较大的彩色图像进行分割时,此时就需要考虑把聚类中心数目筛选的范围进一步扩大,这样就不需要按照步进的方式去筛选聚类中心数目,而是将其与聚类中心点一起纳入遗传算子进行交叉、变异、选择操作,以适应多幅具有较大差别化的彩色图像分割。