基于机器学习的电网信息通信服务器智能优化
申 扬, 于 海, 尹晓华
(国网辽宁省电力有限公司信息通信分公司, 沈阳 110006)
随着中国电网向智能化、网络化、自动化发展,电力信息网络间的信息交互愈发频繁、深入[1]。电网信息通信服务器则承载着电网信息网络信息传输中的核心业务,其上运行的各种应用程序需要处理来自远程的大量小任务[2-3]。电网信通服务器经常面对的是大量的用户请求,而这些用户任务所需的处理时间一般都很短。因此,信通服务器一般采用线程池技术来及时高效的响应这些用户请求。线程池技术是指服务器事先为网络应用程序创建一组线程,当有用户服务请求到来时,可以直接调用线程池中创建好的线程为用户服务;当用户任务执行完成后,这一组线程并不随之销毁,而是等待下一批用户的服务请求。
线程池在提高系统性能的同时,也提出了一个新问题,即如何选择一个合适的线程池大小,以获得最佳的服务器性能。如果线程池的尺寸选择过大,虽然会增加线程池并行处理用户任务请求的能力,但同时也增加了系统为维护如此多数目线程而产生的更多的系统开销;另外,线程数目越多也必然导致系统资源的竞争越发激烈,很可能会导致系统的性能反而下降。而线程池的尺寸选择过小,又会削弱线程池并行处理用户请求的能力。因此,选择合适的线程池尺寸成为决定服务器性能的关键因素。
目前,对于线程池大小的选择有很多不同的解决方法。文献[4]给出了一种基于POSIX(portable operating system interface of UNIX)线程库的线程池反馈算法;通过对线程池响应时间和吞吐量进行监控,对线程池的下一步行为进行决策,调整线程池中的线程数及线程单次处理的任务数。文献[5]采用灰色系统理论预测算法来预测需要线程的数量,使线程池中线程的数量与所需值保持一致,为在服务器使用效率提高的同时保证用户的服务质量提供了一个解决方案,并将这种线程池技术应用于电话缴费系统的设计,获得了良好的效果。文献[6]通过分析影响线程池性能的因素,提出了一种基于系统载荷变化的自适应线程池调节策略。文献[7]分析了任务在线程池中的处理过程,以及当线程池在最佳大小时任务在线程池各阶段所需时间,并给出了一种根据时间等因素来判断系统性能并且动态改变线程池大小的策略。文献[8]提出一种基于反馈技术的自适应线程池调度管理框架,该框架以系统管理人员的先验性知识为基础,在运行过程中不断学习和提取新的知识,通过动态在线调整使得线程池规模保持在与应用需求和计算资源相适应的合理水平。文献[9]利用灰狼寻优算法搜索支持向量机的最优超参数来提升其预测性能,实验结果表明灰狼支持向量机模型具有较高的预测精度、良好的稳定性和泛化能力。
可见,对于线程池调优的研究正逐渐展开,各种理论和方法从不同角度和方向上进行研究。在此背景下提出一种基于支持向量机的线程池尺寸智能优化模型,以适应不同情况下需要不同的最佳线程池大小。首先通过大量的信通服务器性能实验数据构造原始训练样本集,然后经过改进的流体搜索算法优化支持向量机的超参数,最后通过训练好的支持向量机预测不同电网场景下的最优线程池尺寸,从而实现对信通服务器动态智能调优。
1 基于支持向量机的线程池调优模型
面对电网信通服务器的应用场景,线程池技术是解决电网信息网络中大量生产管理业务的有效方案,线程池的性能直接影响了信通服务器的性能。对于线程池性能进行优化,便可以达到优化服务器性能的目的。因此,首先需要对影响线程池性能的因素进行分析,从而进一步建立线程池性能调优的模型。
1.1 线程池性能模型
考虑用户任务响应时间包括了用户任务在任务队列中的队列等待时间以及任务在线程池中的池中处理时间。设用户任务响应时间为t响应,任务在队列中的排队等待时间为t排队,任务在线程池中的池中处理时间为t池,则t响应=t排队+t池。
一个任务在线程池中的处理时间包括任务抢占CPU(central processing unit)的运算时间t运算和任务因等待系统资源而被挂起的等待时间t等待,即t池=t运算+t等待。因此最终用户任务响应时间t响应=t排队+t运算+t等待。
任务排队时间t排队是指用户任务进入任务队列排队开始至线程 池取走任务为止的时间。任务排队时间一方面受用户任务的数量即系统吞吐量m影响;另一方面受线程池的影响,也就是线程池在单位时间内能取走多少任务队列中的任务数。线程池的影响又包括两个方面,一个是线程池尺寸n,线程池越大,容纳的线程数越多,那么单位时间内从任务队列中取出来的用户任务数也就越多;另一个是线程池内任务的“流速”,也就是用户任务在池内所停留的时间——池内处理时间t池。因此,任务排队时间的数学模型为
t排队=f(n,m,t池)=f(n,m,t运算+t等待)
(1)
任务运算时间t运算是指用户任务进入线程池后抢占CPU执行任务所消耗的时间。对于每个用户任务而言,其运算时间可认为是一个常数,与吞吐量、线程池尺寸等其他参数无关,t运算=T运算。
任务等待时间t等待是指用户任务在线程池内因为等待系统资源而被阻塞挂起到重新执行所需的时间。它不仅包括因等待系统资源所阻塞消耗的时间T阻塞,而且包括阻塞结束进入就绪状态后等待CPU调度的时间。显然,等待CPU调度的时间与线程池内的线程个数即线程池尺寸n有关,同时也与池内线程占用CPU运算的时间T运算有关。因此任务等待时间的数学模型可写为
t等待=g(n,T运算,T阻塞)
(2)
综上所述,反映线程池性能的用户响应时间的数学模型可建为
t响应=t排队+t运算+t等待=
f[n,m,T运算+g(n,T运算,T阻塞)]+
T运算+g(n,T运算,T阻塞)
(3)
最后可写成
t响应=h(n,m,T运算,T阻塞)
(4)
欲使线程池性能达到最优,也就是令用户任务响应时间t响应取最小值。如果式(4)连续可微,则取到最小值的必要条件为
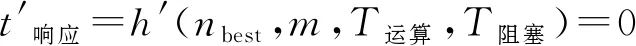
(5)
这是关于nbest、m、T运算、T阻塞的隐函数关系,对于任意不同的3个变量,总会有最后一个变量与之对应,使得用户任务响应时间达到最小,也就是使得线程池的性能达到最优。因此,可以得出,影响线程池性能的因素为吞吐量、任务运算时间、任务阻塞时间和线程池尺寸。对于实际情况而言,吞吐量、任务运算时间和任务阻塞时间都属于用户任务部分,是无法强制调整的。而线程池尺寸却可以在线程池程序中动态调整,来适应客观的用户任务变化,达到线程池调优的目的。
1.2 支持向量机理论
机器学习实质上是通过对训练样本集中各特征变量x与对应类别变量y之间的关系进行学习,来得到特征变量与类别变量之间函数关系的一种算法。因此,可以将吞吐量、任务处理时间和任务阻塞时间看成是特征变量的3个属性,而最佳线程池尺寸看成是分类变量,对于不同的特征变量,都可以归到相应的最佳线程池尺寸类别当中。通过机器学习算法的学习,来得到不同的特征变量与不同的最佳线程池尺寸之间的对应函数关系。
机器学习中,支持向量机(support vector machine, SVM)是一种具有较强泛化能力的智能方法[10-11]。支持向量机的原理是,设输入训练样本点(xi,yi),i=1,…,n,x∈Rn,y∈{-1,+1},分开的超平面方程为(ω·x)+b=0。该超平面方程可有无数个,其中最优超平面可由式(6)求解:
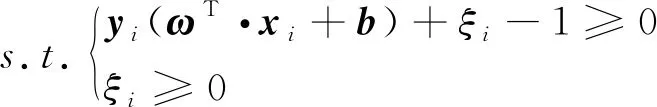
(6)
式(6)中:C为惩罚因子;ξ为松弛变量。
引入拉格朗日因子αi并将其转化为对偶问题可得:

(7)


(18)
于是最优超平面方程为

(9)
式(9)中:SV为支持向量集;求和实际上只对支持向量进行。由此可以通过判断y的取值来对未知样本进行分类。
对于非线性情况,可通过引入核函数K(x·y)=φ(x)·φ(y)的办法将其转化为高维特征空间的线性划分问题,由此可得非线性支持向量机的对偶问题为
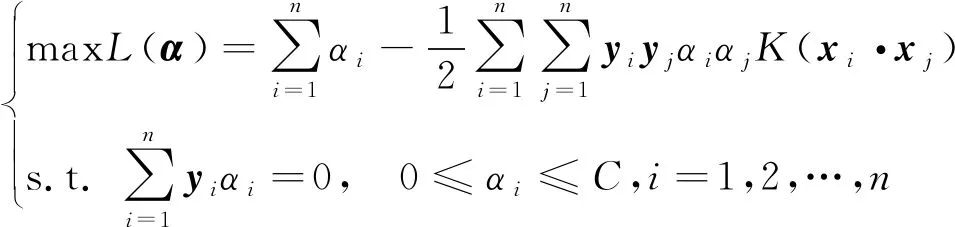
(10)
由此,只要求出此问题的解,即可得到最优分类超平面。支持向量机的决策函数为
K(xi,x)=φ(xi)T·φ(x)
(11)
常用的核函数包括线性核函数,多项式核函数以及径向基核函数等。由于径向基核函数更加具有将非线性分类问题,映射为无限维空间的线性分类问题的能力,因此在支持向量机的研究中得到了广泛应用。径向基核函数的定义为
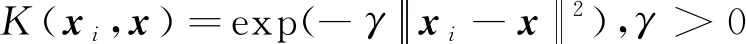
(12)
式(12)中:γ为径向基核函数的参数。
1.3 基于支持向量机的线程池调优模型
通过实验得到的线程池性能数据吞吐量、任务运算时间、任务阻塞时间以及最佳线程池尺寸,构成训练样本集中的一个样本。其中,吞吐量、任务运算时间、任务阻塞时间构成了样本中的三个特征属性,而最佳线程池尺寸则构成样本的分类标签。通过支持向量机的学习训练,得到特征属性与分类标签之间的对应关系。这样,在新的特征数据也就是测试样本到来时,便可以根据此对应关系得到测试样本所对应的分类标签,即最佳线程池尺寸,从而为线程池的大小调整给出依据。
可见,线程池调优的效果直接与支持向量机训练样本集的选取有关,训练样本选取的越全面,则得到的最佳线程池尺寸就会越精确。同时,由于实际情况的复杂多变,对于事先选好的固定的训练样本集也应该有所改变,才能适应不断变化的新情况的出现。为此,将监测得到的线程池特征数据通过一定的条件进行判断,符合条件的则用来动态更新训练样本集,而不符合条件的则直接舍弃。图1给出了基于支持向量机的线程池调优模型框架。具体步骤如下。
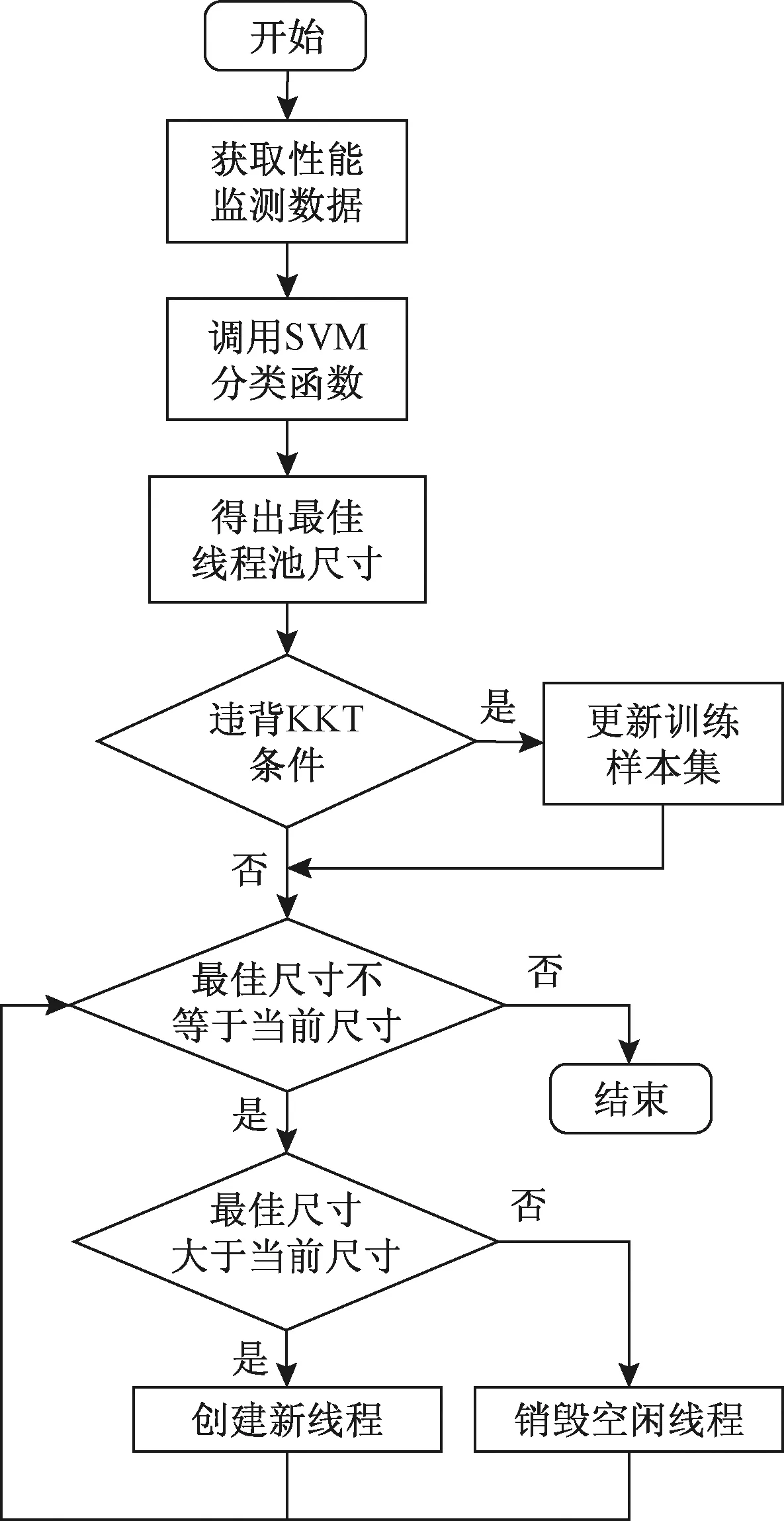
图1 基于支持向量机的线程池调优模型框架
步骤1首先通过实验对线程池性能特征数据进行分类,以吞吐量、任务运算时间和任务阻塞时间为特征变量,根据最佳线程池尺寸分为多类,构造初始训练样本集。
步骤2通过支持向量机进行训练学习,得到各最佳线程池尺寸的分类超平面。
步骤3将实时运行的线程池性能监测数据作为测试样本输入支持向量机中,得到所属的最佳线程池尺寸类别。
步骤4判断所得最佳线程池尺寸是否与当前尺寸相符,如果不符则重新设置线程池,动态调整线程池大小。
步骤5判断特征数据是否满足KKT(Karush-Kuhn-Tucker)条件,如果满足,则替代训练样本集中最违反KKT条件的点,返回步骤2;如果违反,则舍弃忽略。
在基于支持向量机的线程池调优模型中,将KKT条件作为训练样本集更新的判定条件。如果测试样本满足KKT条件,说明这个样本也会落入支持向量的区域内,对分类决策函数会有贡献,需要更新训练样本集,重新训练支持向量机;反之,如果测试样本不满足KKT条件,则不会落入支持向量区域内,对回归决策函数将不会起作用,也就无需再重新训练支持向量机。
对于训练样本集,应该维持一个固定大小的规模,而不应该随着新样本的不断引入而样本集无限增大。因此,在引入新样本的同时,需要剔除对分类决策函数作用最小的样本,即违反KKT条件最严重的样本,这样可以使训练样本集的数目保持不变。
2 基于改进流体搜索优化算法的支持向量机模型
支持向量机的预测性能,由惩罚因子C与径向基核函数的参数γ共同决定。因此,如何适当的选择C与γ,以使得SVM的预测性能达到最优,就成为SVM研究领域中的一个热门问题[12]。比较直接的方法是采用穷举法,但运算量较大,且未必能搜索到最优的参数组合。更多的方法是采用群智能优化算法,来搜索最优的参数组合。引入了相对较新、性能较好的流体搜索优化算法,以期提高支持向量机的预测性能。
流体搜索优化算法(fluid search optimization,FSO)是2018年由Dong等[13]根据流体力学伯努利原理而提出的一种新的启发式优化算法。根据伯努利原理,流体从高压流向低压,并自发地充满整个空间。基于该思想,将待优化的适应度函数值定义为FSO中的流体压力,优化过程模拟流体自发地从高压流向低压的过程。在对不同的工程优化问题进行的试验表明,流体搜索优化算法在一些问题上的优化精度超过了其他一些常见的群体优化算法[13]。但原始的FSO经常容易陷入局部最优,且运算量较大。因此,论文提出一种改进的流体搜索优化(IFSO)算法,以搜索构造最优的支持向量机。
基本的FSO算法步骤如下。
(1)初始化各个流体粒子的位置并调整参数。初始化流体粒子速度Vi=0,流体运动方向direction=0, 流体密度ρi=1,以及常压p0=1,i=1,2,…,n。
(2)计算目标函数值,更新最优目标函数值ybest,最优位置Xbest以及最差目标函数值yworst,计算流体粒子密度ρ=m/lD。
(4)计算其他流体粒子对当前粒子的压强:


(13)
速度方向为

(14)
(6)位置更新:Xi+1=Xi+Vi。
(7)重复步骤(2)~步骤(6),直到满足终止条件。
由于原始FSO算法的运算量较大,且容易陷入局部最优,因此根据支持向量机优化的实际情况,做了以下两点改进。
改进1由于步骤(4)中压强方向的计算量较大,将其简化为

(15)
改进2为了提高流体搜索算法的精度,采用两阶段的优化机制:即第一阶段的多样化搜索和第二阶段的精细化探索。当迭代次数在第一阶段结束时达到特定阈值M′时,搜索空间会缩小到当前最优值附近,并且像元长度会按指数减小,即l=le(M′-t)/σ进行精细化探索,其中σ可以设置搜索的精度。
图2给出了基于IFSO的支持向量机算法。首先通过IFSO随机初始化SVM的超参数C与γ的值,然后赋值给SVM进行交叉训练,得到的SVM分类准确率作为IFSO的适应度函数进行迭代寻优,最终搜索到最优的SVM超参数。
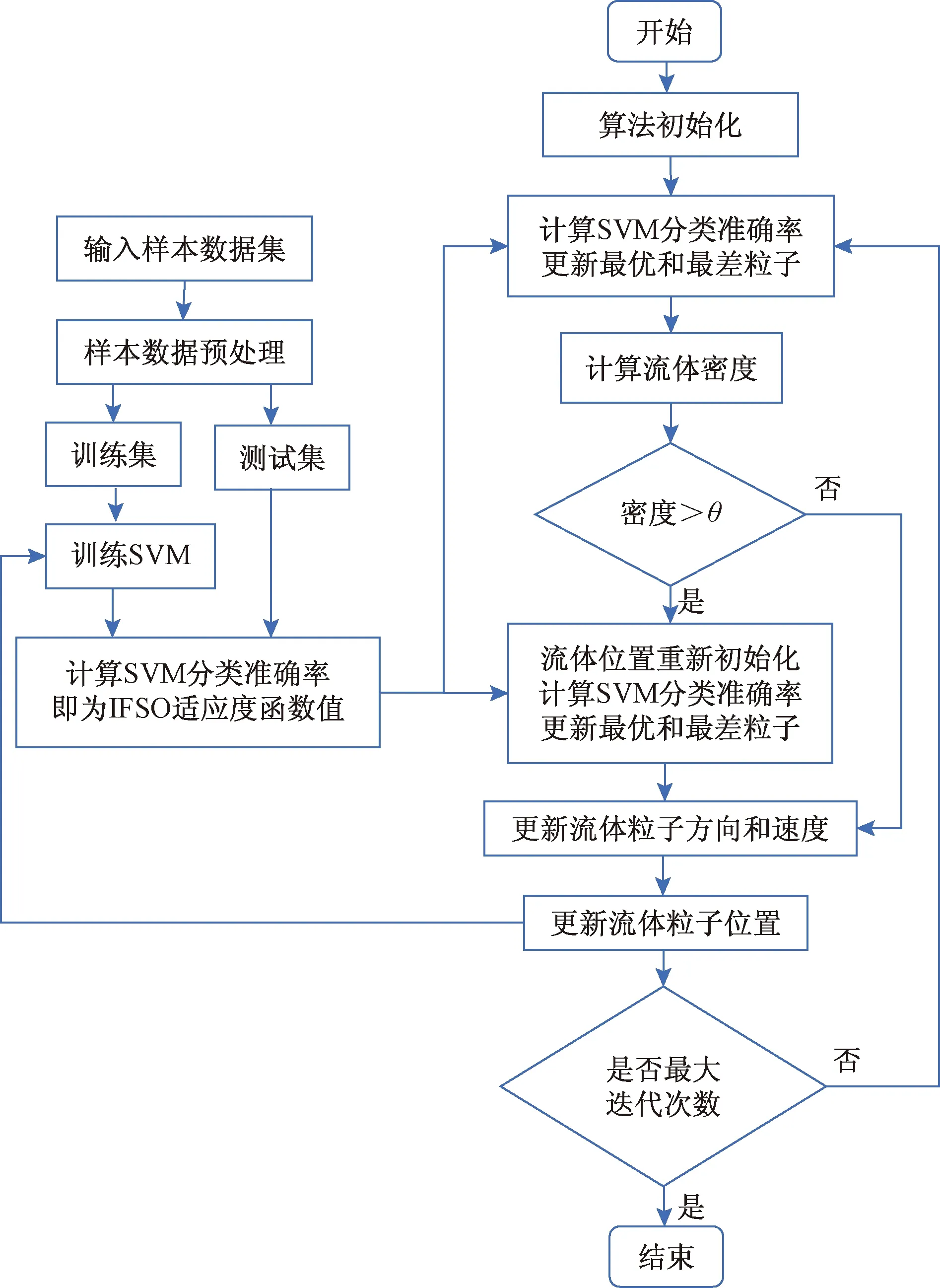
θ为密度极限比例
3 实验结果
3.1 实验数据和环境
以辽宁省电网信息通信服务器(服务器主要配置:CPU为2.4 GHz Intel Xeon E5-2665,内存为32 G,硬盘为10 T。)实时采集的吞吐量、任务运算时间和任务阻塞时间为特征变量,通过支持向量机来智能调整线程池尺寸大小。数据采集间隔为每15 min采集一组服务器特征数据,共采集一周工作日时间得到160组数据。160组特征数据通过仿真实验,将用户任务响应时间作为服务器性能的评价指标,确定最佳线程池尺寸大小,构造训练样本集。
同时,为了消除采集数据特征之间的量纲影响,有利于SVM的训练,对特征数据进行了归一化处理。
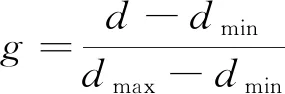
(16)
式(16)中:d为特征数据原始值;dmin为特征数据中的最小值;dmax为特征数据的最大值;g为归一化后的特征数据值。归一化后的部分训练样本集数据如表1所示。

表1 归一化后的部分训练样本集数据
3.2 改进流体搜索优化的SVM训练结果
为了验证IFSO-SVM的表现,实验对比了原始流体搜索算法FSO-SVM,粒子群优化算法(particle swarm optimization,PSO-SVM)以及人工蜂群算法(artificial bee colony algorithm,ABC-SVM)的实验结果。支持向量机分类器采用开源软件LIBSVM,通过5折交叉验证评估模型的平均分类准确率。各算法参数设置如下:粒子数目设为30,最大迭代次数为50。其中FSO与IFSO的参数设置如下[13]:密度极限比例θ=20%,多样化搜索比例M′=0.7,σ=40;粒子群参数设置[14]如下c1=c2=2,ωbegin=0.9,ωend=0.2;人工蜂群算法参数[15]为Ponlooker=Pemployed=0.5;萤火虫算法[16]α=0.5,βmin=0.2,γ=1。根据Lin等在文献[17]中的建议,SVM中参数C的搜索范围为[0.01,350 00],γ的搜索范围为[0.000 1,32]。
从表2中可以看出,IFSO-SVM获得了所有对比算法中最高的分类准确率。其后依次是ABC-SVM、FSO-SVM, FA-SVM及PSO-SVM。改进后的IFSO-SVM比原始的FSO-SVM的平均分类准确率高了1.82个百分点,比位于第二位的ABC-SVM高出了1.61个百分点。可见,对FSO的改进使其更容易搜索到全局最优解,提升了SVM的分类准确率。
图3给出了不同算法优化SVM得出的分类准确率的迭代曲线图。可以看出,在迭代初始时,由于SVM参数由各算法随机初始化,因此得到的分类准确率基本相同,均在85%左右。随着搜索迭代的进行,IFSO-SVM经过不断提升,最终获得了比其他优化算法更高的分类准确率,明显高出下方的ABC-SVM和FSO-SVM的结果。值得注意的是,原始的FSO-SVM的表现略差于ABC-SVM,而IFSO在迭代过程中均优于原始FSO的分类准确率,说明IFSO的改进增强了FSO的搜索效果,使其更容易跳出局部最优,能够得到更好的分类效果。

表2 各对比算法优化支持向量机所得的分类准确率
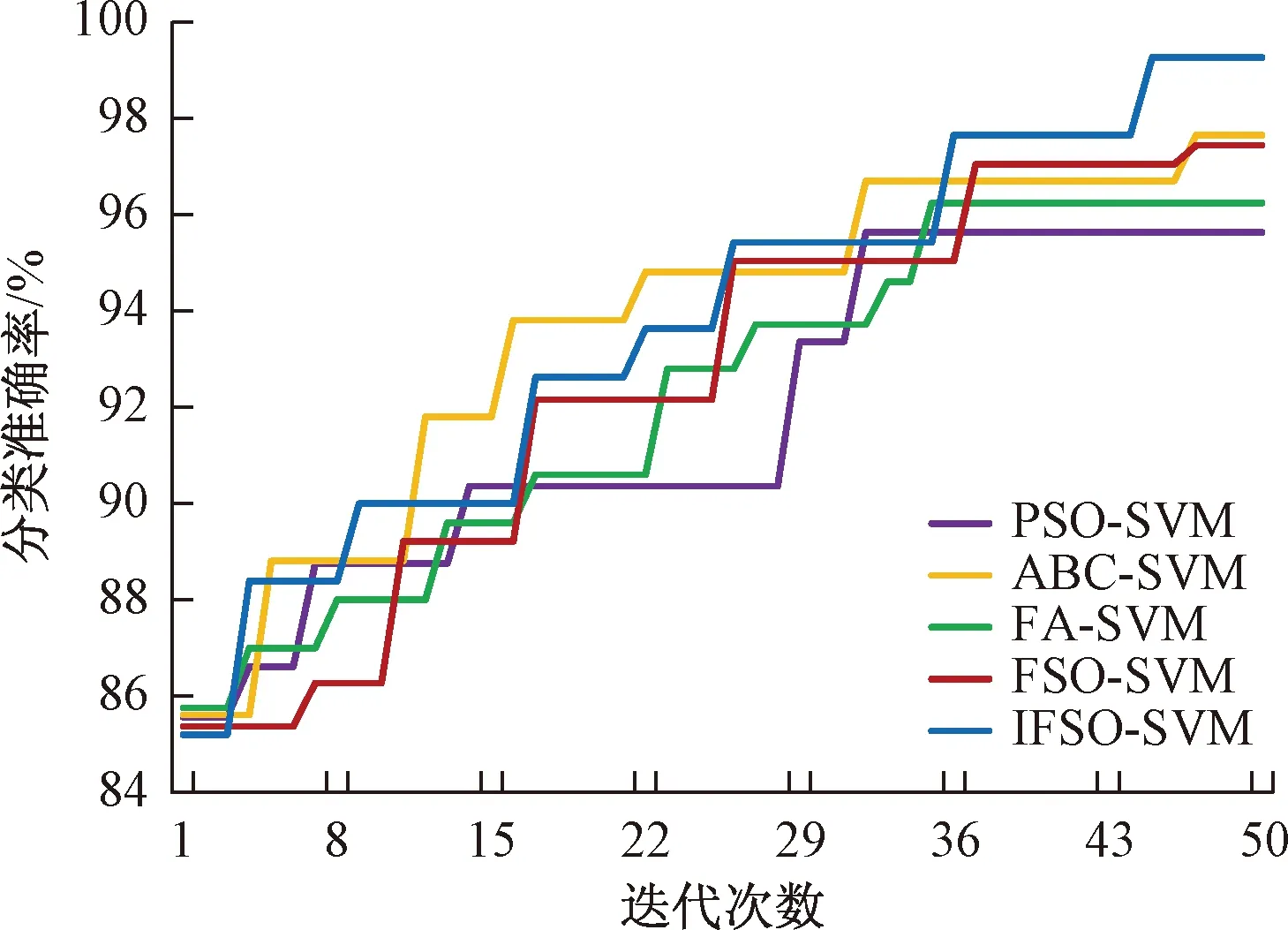
图3 不同算法优化SVM的迭代曲线
3.3 服务器性能测试实验
下面给出电网信通服务器某次突发访问量增多的性能测试结果。图4给出了不同的优化算法智能调整的动态线程池与静态线程池(线程池尺寸固定为30)性能的比较结果,动态线程池调整间隔为1 min。整个实验持续了45 min,其中11~33 min为访问量的高峰期。从图4中可以明显看出,基于各种优化算法的智能动态池性能要明显好于静态池的性能。而在各种优化算法动态池对比中,原始的FSO-SVM与ABC-SVM的测试结果相当,与SVM训练时的结果类似。而基于IFSO-SVM动态池的用户响应时间要比其他对比算法更少。尤其在访问量高峰期时,IFSO-SVM动态池的用户响应时间的上升明显比其他优化算法更加平缓,表明了IFSO对原始FSO的改进起到了较好的效果,能够智能地对服务器响应时间进行削峰的作用。
表3给出了IFSO-SVM相较于不同算法的效率提升结果,包括45 min之内平均效率提升结果,最小效率提升结果以及最大效率提升结果。可以看出,动态调优的线程池性能比静态池的性能均有明显改善,且IFSO-SVM相较于其他对比算法平均会有9.12%~38.00%的提高。因此,可以得出结论,基于IFSO-SVM动态线程池算法对信通服务器性能的智能优化具有良好的效果。
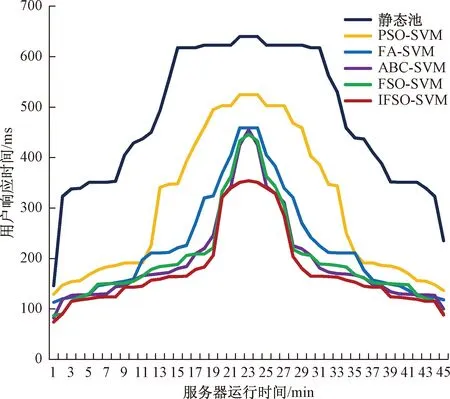
图4 不同算法动态池优化与静态池性能的比较
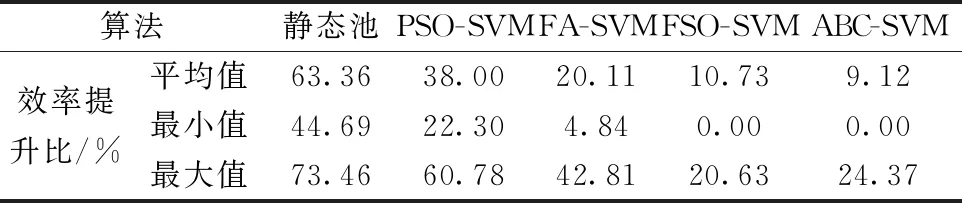
表3 IFSO-SVM相较于不同算法的效率提升百分比
4 结论
提出一种基于支持向量机的信通服务器动态线程池智能调优模型。通过大量的信通服务器性能实验数据构造原始训练样本集,然后采用改进的流体优化算法搜索支持向量机的超参数,最后通过训练好的支持向量机预测不同电网场景下的最优线程池尺寸,从而实现对信通服务器动态智能调优。在某省电网信通服务器的性能实验中,相较于其他优化算法,得出以下结论。
(1)基于IFSO-SVM的动态线程池技术获得了更高的分类准确率,提高了FSO的优化效果,使其更容易跳出局部最优。
(2)基于IFSO-SVM动态池能够智能地减少服务器的用户响应时间,尤其在访问高峰时能够起到削峰的作用,提升了服务器的执行效率。
但IFSO算法本身超参数的选择也是一个不断尝试的过程,未来可进一步研究是否可以自适应选择IFSO的超参数,进一步提高服务器优化过程的智能性。

