基于NTRU的密文域可逆信息隐藏算法

周 能， 张敏情， 唐洪琼， 周昊楠， 柯 彦， 狄富强

(武警工程大学密码工程学院,网络与信息安全武警部队重点实验室, 西安 710086)

传统的信息隐藏算法在嵌入数据后会造成原始载体的永久性失真,不能适用于需要无损恢复出原始载体的应用场合,如云环境下的隐私数据标注、远程医学诊断、司法取证等对载体失真较为敏感的应用领域[1]。而可逆信息隐藏算法[2]兼顾了信息隐藏与原始载体的无失真恢复,得到了广泛研究,主要有差值扩展[3]和直方图平移[4]。随着云服务的推广,出于隐私保护的目的,用户通常要对上传的数据进行加密处理,从而将原始数据变成难以理解的密文数据,云端需要直接在密文上嵌入时间戳、用户身份等信息进行密文管理,密文域可逆信息隐藏应运而生,且已成为最新的研究热点。密文域可逆信息隐藏算法要求用于嵌入的载体是经过加密的,嵌入信息后仍然可以无差错解密并恢复出原始载体。将病人身份、病历报告等敏感信息通过密文域可逆信息隐藏的方法嵌入到密文图像中,可以实现远程医疗图像的密文安全管理。接收者不仅可以可逆恢复载体图像,不影响图像的正常使用,还可以正确提取合法认证信息,保证图像的完整性。综上,密文域可逆信息隐藏算法是加密域信号处理技术与信息隐藏技术的重要结合点,对于数据处理过程中的信息安全具有隐私保护与秘密信息传递双重作用。

目前,该领域的技术难点在于实现载体图像的完全可逆、提高算法的嵌入率以及嵌入信息的不可感知性等方面,相关学者做了大量的研究。按照对图像的加密方式,主要可分为对称密码加密、秘密共享加密和公钥密码加密。对称密码加密计算复杂度低、加解密速度快,例如,文献[5]提出了密文图像上的可逆信息隐藏算法,该算法用流密码加密图像,而后将密文图像分成互不重叠的块,每块有两组,通过翻转相应组中每个像素的3个最低有效位嵌入1 bit信息,接收者通过波动函数提取信息,但当分块小的时候,错误率变高；文献[6]利用能够进行边匹配的波动函数改进了文献[5]的算法,降低了算法提取信息的错误率。上述算法需要在图像加密后留出空间进行信息隐藏,导致算法嵌入率较低,并且数据提取过程中有较高的错误率。文献[7]提出了一种加密前预留空间的密文域可逆信息隐藏算法；文献[8]通过利用数据嵌入的预测误差来提高可逆性、嵌入容量和图像质量。文献[9]利用Shamir(k,n)门限秘密共享设计了密文域可逆信息隐藏算法,该算法将单个像素值作为多项式的常数项,利用秘密共享将原始图像加密成n份,分别发送给n个不同的数据嵌入者,数据嵌入者通过在密文上进行差值扩展或差值直方图平移操作嵌入信息,接收者得到少于k份时无法恢复原始图像；而文献[10]利用的是多秘密共享加法同态的特点结合差值扩展算法进行信息嵌入,该算法将多个像素值作为多项式的系数而不是多项式的常数项,因而提高了算法的加密效率。上述密文域可逆信息隐藏算法利用对称密码和秘密共享加密图像,每一对发送者和接收者都必须拥有不同的密钥,这在当前的多方云计算服务背景下所需的密钥量是巨大的,从而给密钥管理带来了困难。此外,大多数对称密码在将明文数据加密成不可读的密文数据、保护数据安全的同时,会破坏加密后数据的代数结构,导致密文几乎不具有可后续处理的可能性。然而,在现实的云计算环境下,既要求数据处理系统能够保护用户隐私和数据安全,又要求加密后的数据能够进行传统意义上数据处理操作,传统的密码算法不能适应云计算背景下这种新的要求。因此,如何结合公钥密码设计出高性能的密文域可逆信息隐藏算法,实现对加密数据的有效管理及安全保护,是云计算大数据环境下亟需解决的关键问题。

文献[11]提出了基于公钥密码的密文图像可逆信息隐藏,利用公钥密码的特点克服对称加密需要安全通道事先传递密钥的缺点,该算法将1 bit信息嵌入到一对相邻加密像素中,根据Paillier密码体制加密的同态特性,接收端通过比较所有的解密像素对获得秘密信息,其缺点是存在固有的溢出问题；而文献[12-13]通过解决溢出问题改进了文献[11]的算法,文献[12]将不可嵌入位置记为边信息,图像所有者把边信息加密之后发送给数据嵌入者,这样数据嵌入者在嵌入额外信息时就能够避免溢出；文献[13]结合信号能量转移的方法,将一个像素值整数用3个整数来表示,从而避免溢出。文献[14]将湿纸编码(wet paper code, WPC)和Paillier同态加密特性相结合,该算法首先在明文域预留空间,加密后,可通过直方图平移嵌入信息,使得嵌入的信息能够在明文域中提取出来。结合同态加密特性,利用湿纸编码将额外信息无损地嵌入到加密图像中,使得能够在加密域中提取嵌入的信息。该算法利用多个比特位进行嵌入,嵌入率上限为1 bit/pixel。但是,由于使用WPC技术,需要利用高斯消元法求解含k个未知数的一次方程组,且该算法实际上进行了两次的信息嵌入操作；文献[15]利用Paillier密码体制的同态和概率特性,提出了一种基于镜像密文组的密文域可逆信息隐藏算法,由于采用加密前预留空间的方法,增加了明文泄露的风险；文献[16]将EC-EG(elliptic curve ElGamal)应用于密文域可逆信息隐藏,并通过构造镜像中心密文的方法提升了文献[15]中算法的嵌入容量。文献[17]利用基于R-LWE(ring-learning with errors)的浅同态加法特性提出了一种高容量的密文域可逆信息隐藏算法,但该算法只能进行有限次的加法运算；文献[18]利用LWE(learning with errors)提出了一种基于加密过程的密文域可逆信息隐藏算法思想,该算法对LWE加密之后的密文冗余进行重量化和再编码进行信息的可逆嵌入,并通过分析嵌入信息后密文统计特征的变化,推导出携密密文图像的分布函数就等于嵌入信息前密文图像的分布函数,论证了在密文中嵌入信息的不可感知性,但是当明文长度增加时,加密密钥长度也相应增加,造成密文扩展率较高。

综合上述分析,利用公钥密码同态性质进行信息嵌入是该领域的研究热点,而当前大多利用Paillier等公钥密码加密图像。在密码学中,对于用什么公钥密码体制来代替正在广泛应用的RSA(rivest shamir adleman)和ECC(elliptic curve cryptography),主要有以下3个解决方案：NTRU(number theory research unit)公钥密码体制、McEliece公钥密码体制、MQ(multivariate quadratic polynomials)公钥密码体制。McEliece公钥密码体制基于纠错码问题,虽然安全性强,但是计算效率低；MQ公钥密码体制基于有限域上的多变元二次多项式方程组的难解性,在安全性方面的缺点比较明显；而NTRU公钥密码体制算法简洁、计算速度快、占用存贮空间小。为此,提出了一种基于NTRU的密文域可逆信息隐藏算法。

1 相关技术

1.1 NTRU公钥密码体制

美国布朗大学的Hoffstein、Pipher和Silverman三位数学教授发明了NTRU公钥密码体制[19],由于NTRU产生密钥的方法比较容易,加解密速度比RSA等算法快很多,NTRU成为当前公钥密码体制研究的一个热点。NTRU包括两部分算法：NTRUEncrypt用来进行加密,NTRUSign用来进行数字签名。与其他正在使用的公钥密码体制不同,NTRU可以防止被Shor算法破解,并显著提升了性能。NTRU是一个基于多项式环的密码体制,它的安全性依赖于格中最短向量问题(shortest vector problem, SVP)问题,与基于离散对数或大整数分解等公钥密码体制相比,它有许多优势,在安全性方面的优势更为明显,NTRU算法具有抵抗量子计算攻击的能力,而RSA和ECC算法是无法抵抗量子计算的。主要介绍NTRUEncrypt算法过程[20]。

设多项式φ=xn+1,n为2的幂且n≥8。多项式环R=[x]/φ,Rq=R/qR,q≥5且为素数,这样在Rq中有唯一的φk满足

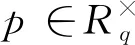
(2)密钥生成。选择n,q∈,。从D中采样得到f′，令f=pf′+1，若则重采样；从D中采样得到g，若则重采样；得到私钥和公钥且

(4)解密。若得到密文C和私钥f，先计算C′=fC∈Rq，则明文为

M=C′modp=[p(gs+ef)+fM]modp∈P

(1)

(5)加法和乘法同态。对明文M1、M2加密得到密文C1=hs1+pe1+M1∈Rq、C2=hs2+pe2+M2∈Rq，则加法同态为

f(C1+C2)=p[f(e1+e2)+g(s1+s2)]+

f(M1+M2)≜

(pEadd+f(M1+M2))modp

(2)

乘法同态为

f2(C1C2)=p[pg2s1s2+gs1f(pe2+M2)+

gs2f(pe1+M1)+

f2(e1M2+e2M1+pe1e2)]+

f2(M1M2)≜

(pEmult+f2(M1M2))modp

(3)

即两密文相加在解密后等于明文相加、两密文相乘在解密后等于明文相乘。

1.2 游程长度编码

游程长度编码(run length coding, RLC)是一种与载体性质无关的无损数据压缩技术，其原理是用整数对(L，R)来表示游程序列，游程序列是指连续出现且相等的数字序列。例如对连续的二进制序列11110000001100000000进行RLC压缩，由于游程编码默认从0开始计数，而二进制序列的起始位是1，所以0的数量是0，接着1的数量是4，依次类推得到编码结果为04628。实验图像中存在不可嵌入位置，所以用0、1分别标记可嵌入像素和不可嵌入像素位置得到位图，再利用RLC压缩位图得到边信息(side information, SI)。边信息的作用是让接收者知道信息嵌入在图像中的位置，实现图像的完全可逆恢复。

2 算法

2.1 设计思想

主要利用NTRU算法的加法同态性质进行信息嵌入、利用差值扩展算法进行预处理和可逆恢复。算法流程如图1所示，由图像所有者O、数据嵌入者H、接收者R构成，算法主要包括参数设置、数据预处理、加密与信息嵌入、解密与信息提取等过程。

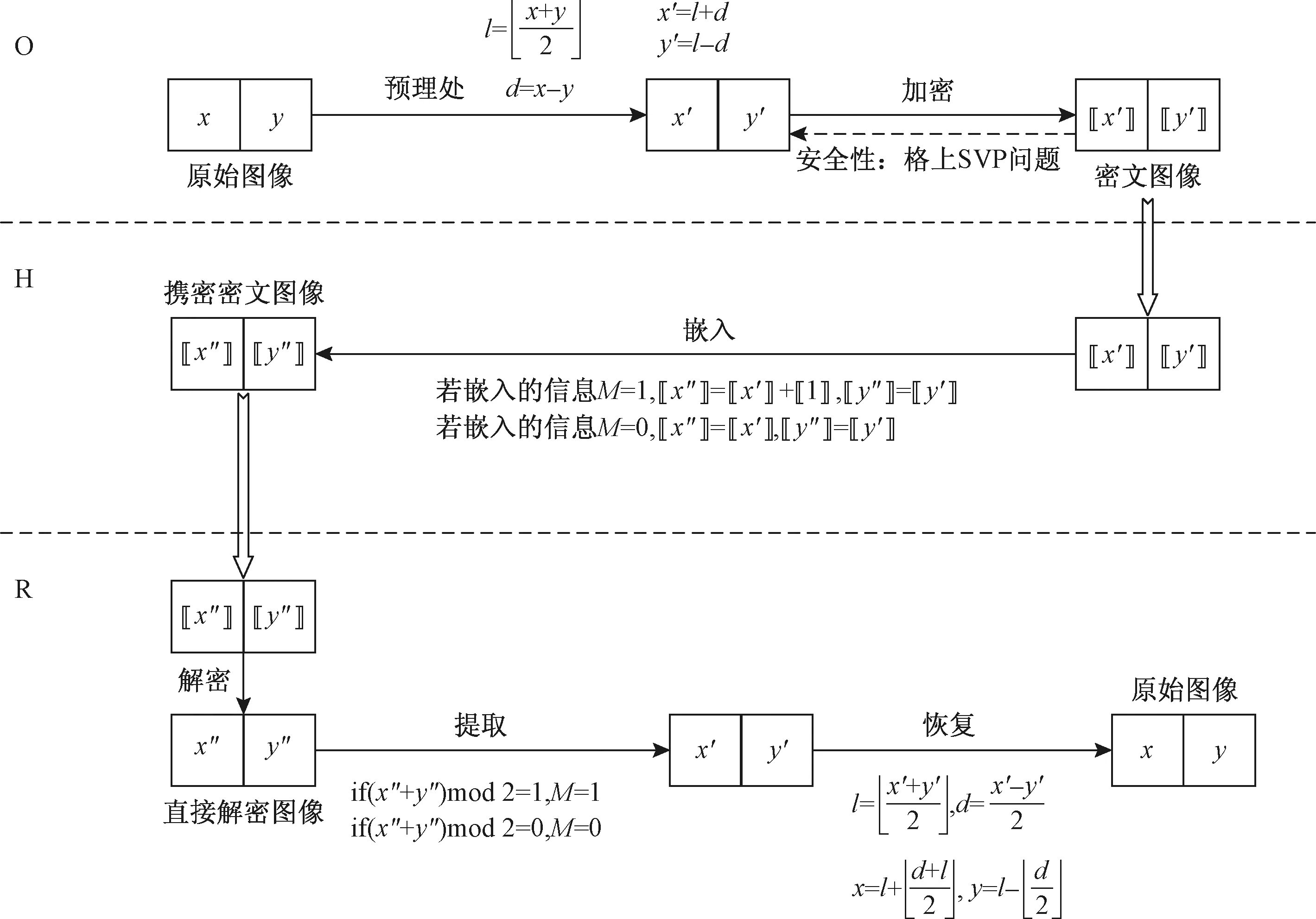
图1 算法流程

2.2 算法过程

2.2.1 参数设置

选择参数n、q、p、α、σ，则多项式φ=xn+1，n为2的幂且n≥8。多项式环R=[x]/φ，Rq=R/qR，q≥5且为素数，在Rq中有唯一的φk满足

2.2.2 数据预处理

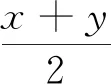
2.2.3 加密与信息嵌入

2.2.4 解密与信息提取

wx′+M=f(Cx′+Cm)modp

=p[f(e1+e3)+g(s1+s3)]+f(wx′+M)≜

(pEadd+f(wx′+M)modp

(4)

wy′=fCy′modp=

[p(gs+ef)+fwy′]modp

(5)

得到嵌入信息后的二进制明文，将其转换成十进制后，得到嵌入信息后的十进制明文，记为(x′,y′)。

(2)信息提取。若(x′+y′)mod2=1，则提取秘密信息M= 1；若(x′+y′)mod2=0，则提取秘密信息M= 0。

2.2.5 可逆恢复

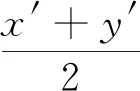
2.3 边信息处理

在可逆信息隐藏中，边信息在可逆恢复过程中十分重要。本文算法的边信息由差值扩展产生，当像素对(x′,y′)中任一像素的值不在图像灰度[0, 255]的范围内，就用数字1标记为不可嵌入位置。图像中的不可嵌入位置是少数，即位图中1是少数，大多数是0，图像所有者可以将位图利用RLC压缩后作为边信息传递给数据嵌入者和接收者，实现图像的完全可逆恢复。

3 算法分析与仿真实验

为测试本文算法性能，选用USC-SIPI图像库中大小为512×512的8位灰度图像进行实验，如图2所示。为了实验数据的全面性，既有平滑图像，如Lena，又有纹理复杂图像，如Baboon。在MATLAB中调用NTRUEncrypt算法的C++代码来实现对图像的加解密操作。实验所用的软硬件环境为CPU: Intel(R) Core(TM) i7-5500U @ 3.60 GHz；RAM: 32 GB；OS: Windows 10；Programming: C++ and MATLAB R2015b。

图2 测试图像

3.1 安全性分析

由于文献[20]对NTRU算法的正确性和安全性从数值几何和代数数论的角度进行了详细证明，其安全性可规约到格上SVP问题[21]和BDD(bounded distance decoding)问题[22](SVP问题的一个变种)，因此本节仅讨论所提算法可能遇到的潜在攻击。首先列出安全性分析中用到的几个困难问题定义，然后主要考虑已知明文攻击(known plaintext attack, KPA)和惟密文攻击(ciphertext only attack, COA)。

定义1给定格L的任意一组基，如果能够找到满足下列条件的非零格向量：v∈L，使得|v|=λ1(L)，则称这个问题为SVP问题。

定义2令格L和向量mi[在αλ1(L)距离内]，在距离αλ1(L)内寻找距离mi满足距离条件αλ1(L)的格点Bi∈L是一个α-BDD问题。

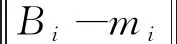
3.1.1 已知明文攻击

在KPA假设下，攻击者可以获取大量的明密文对。攻击者可能会获取参数si、ei，因此，攻击者能够进行下列计算：cj0-cj1=E(mi,2,si,ei)-E(mi,2,sj,ej) =h(si-sj)+2(ei-ej)。但是，根据NTRU问题假设，攻击者不可能获得si和ei，这相当于解决格上SVP问题；且h=pg/f中，g和f从高斯分布D中取样。从攻击者的角度看，密文仅包含伪随机的取样，所以本文算法是KPA安全的。

3.1.2 惟密文攻击

在COA假设下，攻击者可以获取密文，包括加密的界。明文mi和Bi使用相同的公钥和参数si、ei加密，不同的mi对应不同的Bi。攻击者可能会推出界Bi。因此，攻击者进行下列计算：cj0-cj1=E(mi,2,si,ei)-E(Bi,2,si,ei)=mi-Bi。但是，根据BDD问题的困难性，同时mi是加密的，因此攻击者无法获得Bi，即从密文中无法得到任何其他信息，所以本文算法是COA安全的。

3.2 统计特征

在密文域可逆信息隐藏中，对密文中嵌入信息的不可感知性分析较少，也没有统一的标准，文献[1，18]通过分析嵌入信息后密文统计特征的变化，推导出携密密文图像的分布函数就等于嵌入信息前密文图像的分布函数，论证在密文中嵌入信息的不可感知性，而本节则从统计的角度进行定量分析。

图3给出了Lena和Baboon的原始图像和利用本文算法得到的密文图像、携密密文图像。统计分析能够测试算法在混乱和扩散方面抵抗攻击的性能。通过分析原始图像、密文图像、携密密文图像的直方图及其方差、信息熵、相邻像素相关性[23]，能够有效说明加密算法的安全性、嵌入过程对于加密算法安全性的影响以及在密文图像上嵌入信息的不可感知性。

图3 原始图像、密文图像和携密密文图像

3.2.1 直方图及其方差

密文图像的直方图接近均匀分布，并且与原始图像的直方图有明显的差别，在数学计算上体现为密文图像的方差比原始图像的方差小得多，并且图像像素的均匀分布情况可以用方差来度量，方差的计算公式为

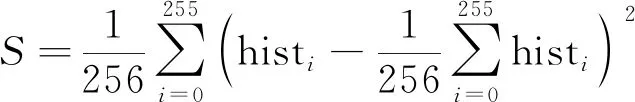
(6)

式(6)中：histi(0≤i≤255)表示图像某一像素值的个数。

3.2.2 信息熵

信息熵可用来度量图像信息的多少，根据Shannon的定理，图像的信息量计算公式为

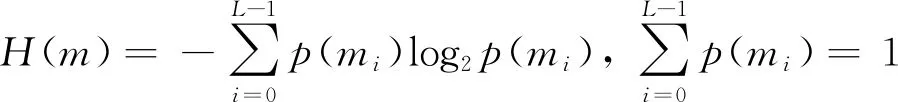
(7)

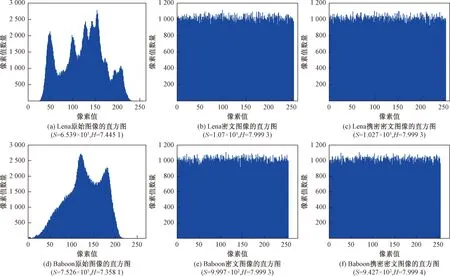
图4 原始图像、密文图像、携密密文图像的直方图与信息熵

式(7)中：图像有L种灰度mi，且对应的概率分别为p(mi)。称H为图像的信息熵。从理论分析来看，信息熵越大，灰度图越接近均分分布，对于一幅无任何失真的灰度图像，文献[23]证明其信息熵等于8。

图4所示为原始图像、密文图像、携密密文图像的分布直方图，计算各组图像实验结果的方差和信息熵，分别记为S和H。图4表明携密密文图像的直方图与原密文图像的直方图相比没有出现明显变化，而嵌入信息的过程可看作噪声微扰导致密文图像变化的过程，因此对密文图像的分布特性基本不会发生破坏。对图4的直方图中数据计算平均信息熵，结果表明携密密文图像的信息熵不低于原始密文图像，基本接近于加密域中数据等概率分布时的最大信息熵。

3.2.3 相邻像素相关性

原始图像的相邻像素相关性系数应接近于1，密文图像的相关性系数应比1小很多，表明原始图像与密文图像的相邻像素相关性是完全分开的。图像相邻像素相关性系数rxy(rxy∈[-1, 1]，-1表示负相关，1表示正相关)的计算公式为

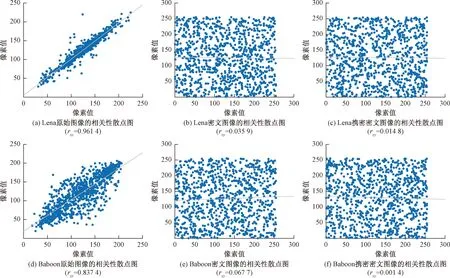
图5 原始图像、密文图像、携密密文图像的相关性散点图

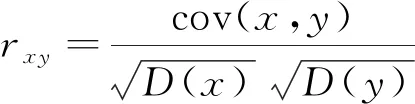
(8)

式(8)中：

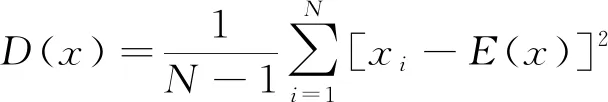
(9)

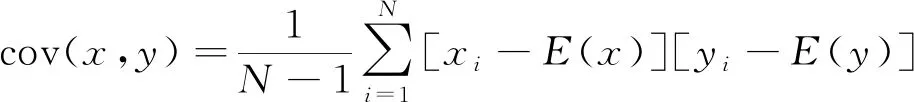
(10)

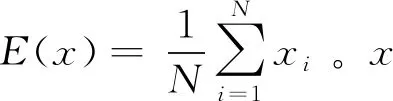
各从原始图像、密文图像、携密密文图像中随机选择1 000对水平、垂直、对角3种相邻像素，计算平均相关性系数，记为rxy，结果如表1所示。通过对表1中原始图像、密文图像、携密密文图像的相邻像素相关性进行分析对比，可以看出原始图像的相邻像素相关性系数接近于1，说明其相邻像素相关性非常强；密文图像的相邻像素相关性系数远小于1，说明密文图像的相邻像素相关性与原始图像相比是完全分开的，且携密密文图像的相邻像素相关性没有出现明显变化。此外，绘制出的1 000对水平、垂直、对角3种相邻像素相关性散点图从另一方面也验证了上述结论，结果如图5所示。

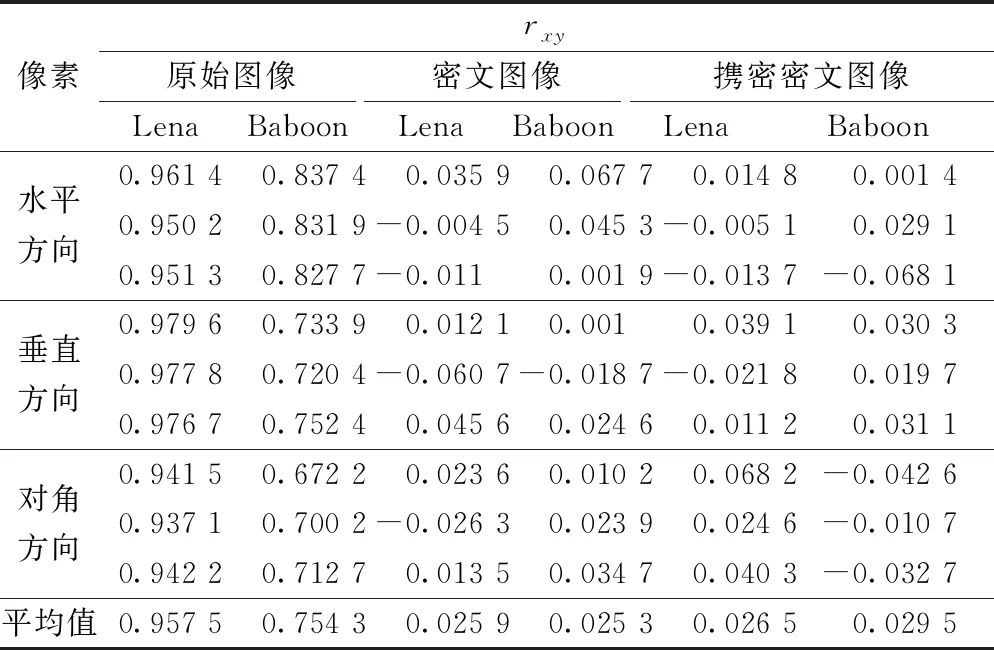
表1 相邻像素的相关性系数

综上，通过对原始图像、密文图像、携密密文图像的直方图及其方差、信息熵、相邻像素相关性进行统计分析，并通过实验验证了NTRU加密算法的安全性和在密文域中嵌入信息的不可感知性。

3.3 峰值信噪比和Q质量因子分析

3.3.1 峰值信噪比

在可逆信息隐藏中，通常用峰值信噪比(peak signal-to-noise ratio, PSNR)评价与原始图像相比较，恢复后图像的质量或失真情况。根据人类视觉系统的特点，通常认为PSNR大于35 dB时，人眼觉察不到图像有明显的失真，PSNR可由式(11)计算：

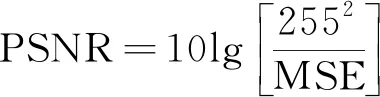
(11)

式(11)中：MSE是原始图像像素矩阵I和恢复图像像素矩阵Ι′之间的均方误差。MSE可由式(12)计算：

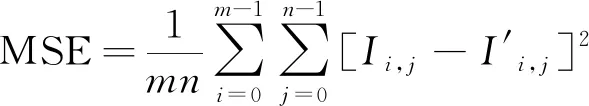
(12)

式(12)中：m×n是图像大小。

在不同嵌入容量(embedding capacity, EC)下测试图像的PSNR，如表2所示。对于平滑图像Lena、Hill、Man，当嵌入容量达到32 768 bits时，其PSNR仍大于35 dB；对于纹理复杂图像Baboon，当嵌入容量少于8 192 bits时，人眼觉察不到图像有明显的失真。选择文献[10，12，15]与本文算法进行性能对比，对平滑图像Lena和纹理复杂图像Baboon的PSNR值实验结果对比分别如图6所示。

文献[10]利用多秘密共享加密图像，多项式在模251的条件下进行运算，所以存在较多的不可嵌入位置，且随着嵌入率的增加，PSNR值下降较快；在文献[15]中，由于自嵌入数据时直方图平移次数增加，再加上构造镜像密文组引起的失真加大，从而导致该算法的性能下降较快，所以本文算法在较高的嵌入率下比文献[15]的PSNR值要高。

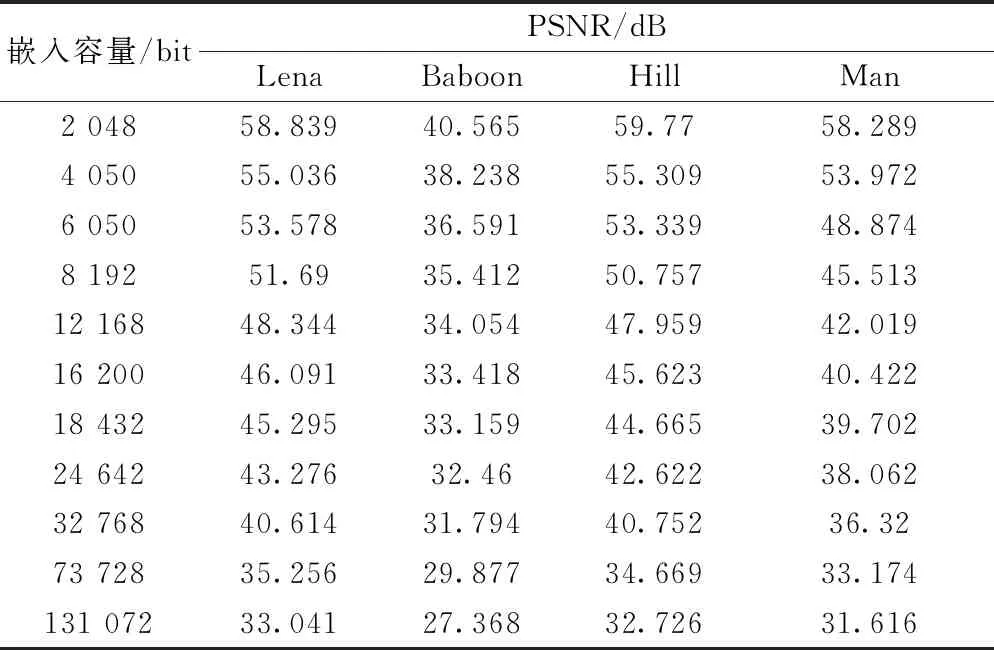
表2 测试图像PSNR的实验结果

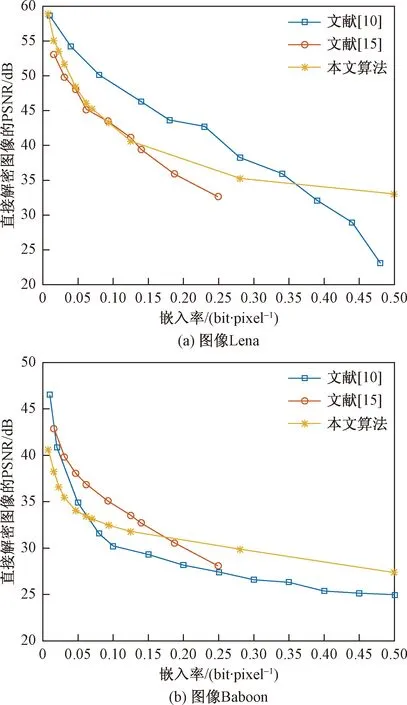
图6 实验结果对比

3.3.2Q质量因子

通过PSNR的大小，可以很清楚地知道嵌入信息后的图像是否会被人的肉眼观测出来。然而，PSNR不能指出嵌入信息前后两幅图像它们之间差别有多大。因此，可利用文献[24]提出的通用质量因子Q来检测图像在嵌入信息前后的相似度有多高。Q质量因子由式(13)计算：

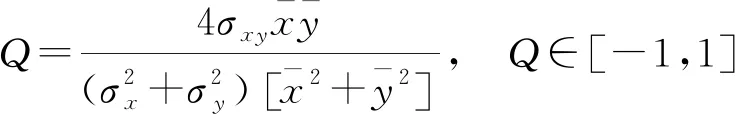
(13)

式(13)中：

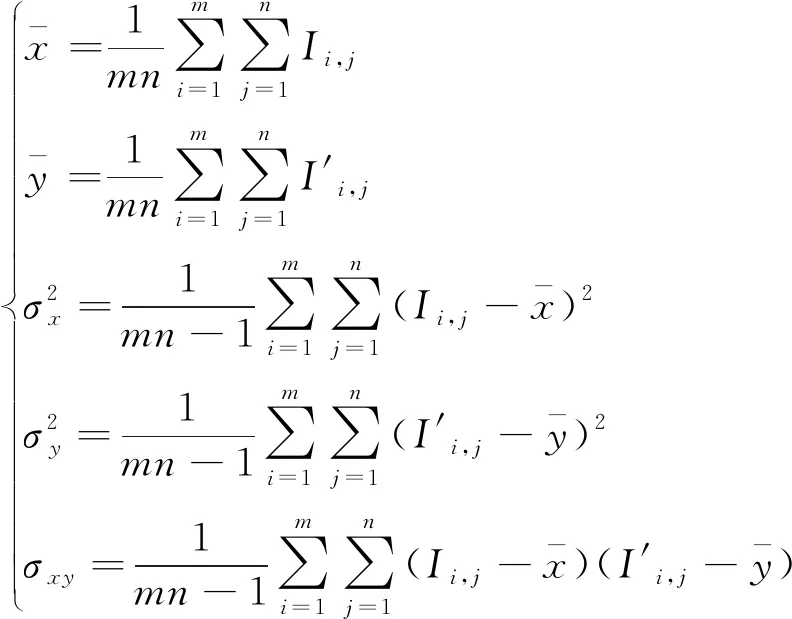
(14)

3.4 嵌入率分析

本文算法的嵌入率(embedding rate, ER)由式(15)计算：

ER=嵌入容量/图像的像素总个数

(15)

表4给出了实验图像随着嵌入容量增加得到的不可嵌入位置、嵌入率和边信息的数据变化情况。由表4可以看出，图像中不可嵌入位置是少数，基本上不影响图像的嵌入率；经过RLC压缩之后的边信息最多，只有241 bits，因而本文算法的辅助开销非常少。

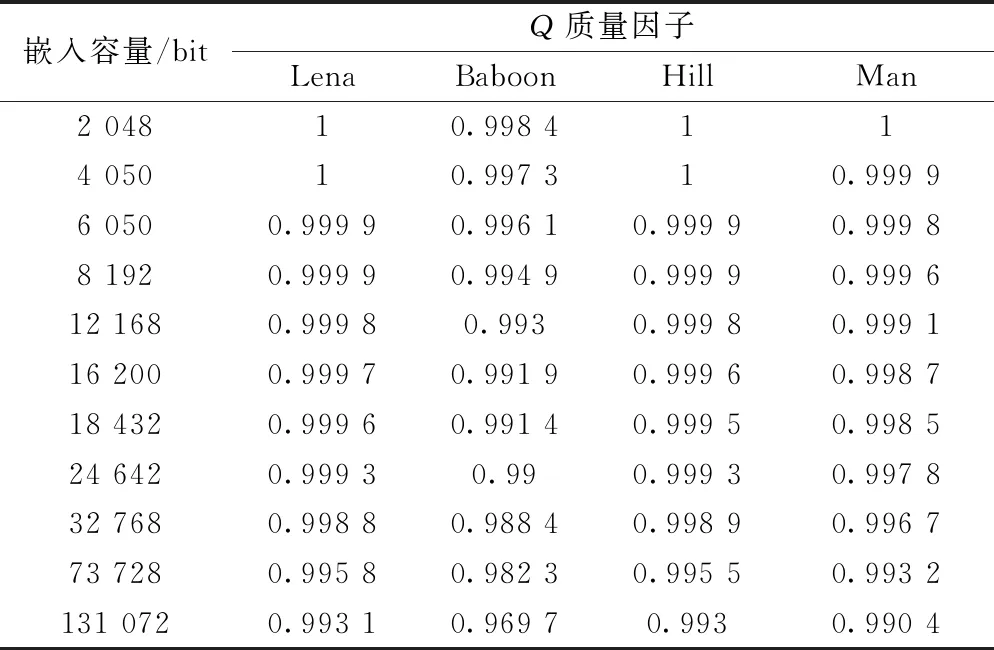
表3 测试图像Q质量因子的实验结果

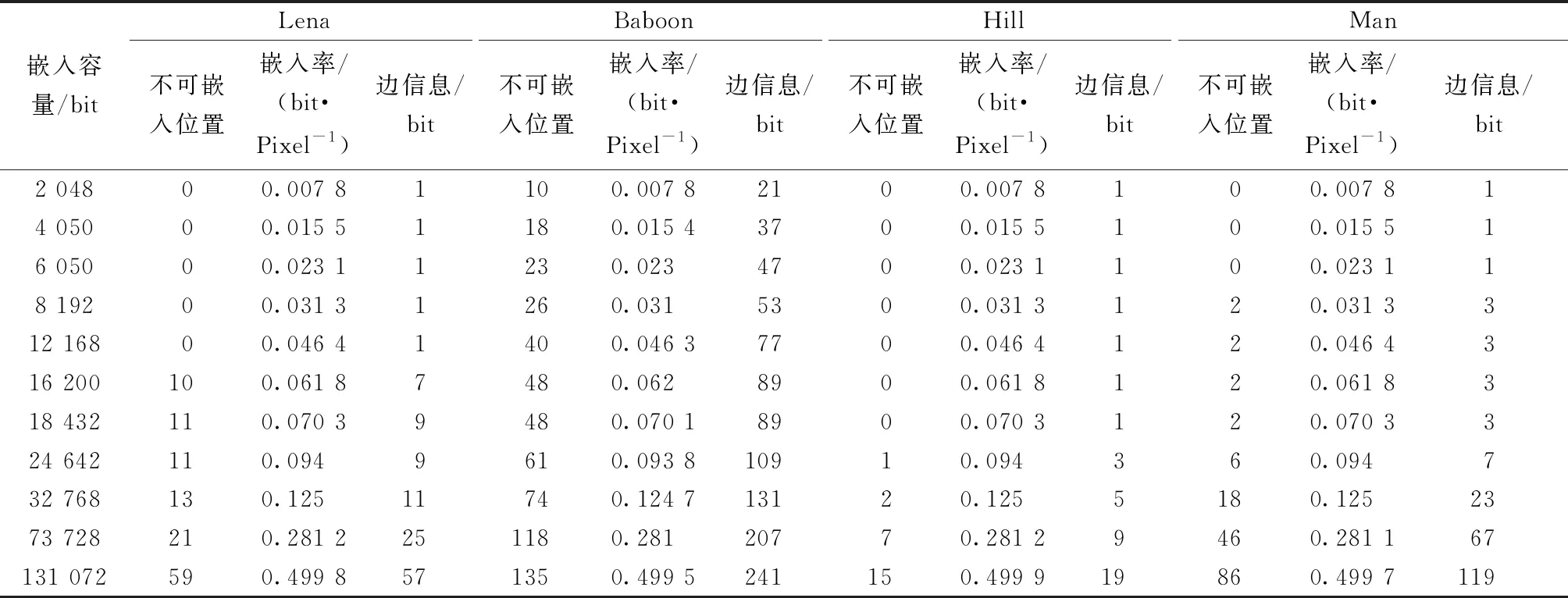
表4 测试图像的嵌入率和边信息

4 结论

提出了基于NTRU的密文域可逆信息隐藏算法，利用NTRU的加法同态特性并结合差值扩展算法进行信息嵌入与提取，保证了嵌入信息的安全性与无失真提取，且确保了载体图像恢复的完全可逆，算法分析与仿真实验说明了加密算法的安全性以及嵌入信息的不可感知性。当前，随着网络安全和隐私保护需求的不断增长，未来将大量使用公钥密码技术，可将本文算法的密文域嵌入提取技术广泛应用，进一步丰富密文域可逆信息隐藏的应用场景。但是由于NTRU算法加密使得图像密文呈现出均匀分布的特征，而嵌入信息的过程可看作噪声微扰导致密文图像变化的过程，因此，如何利用密码学中可证明安全理论进一步论证在密文中嵌入信息的不可感知性将是未来研究工作的一个方向。