基于随机森林算法的函数缺陷定位

李倩倩, 牟永敏*, 赵晓永

(1.北京信息科技大学网络文化与数字传播北京市重点实验室, 北京 100101； 2.北京信息科技大学信息管理学院, 北京 100192)

软件软件缺陷定位[1](software fault location)是指当软件发生失效时,程序人员通过分析源码找到引发该失效的缺陷代码的行为。研究表明,软件的发展和维护的过程中,软件调试则占整个过程中的50%～80%[2],缺陷定位则是整个调试过程中成本较高的重要阶段。传统的缺陷定位通常由开发人员通过运行失败的测试用例并手动设置断点的方式寻找程序中缺陷的位置,然而这种方式未能够充分利用测试用例执行行为和执行结果的信息[3]。

近些年来,研究人员从不同的角度进行深入的研究并取得了阶段性的进展。Wang等[4]则通过识别关键谓词来定位出错误的位置,然而此种方法需要大量的测试用例；为了降低程序之间的依赖关系对于缺陷定位的影响,借助于基于程序切片的缺陷定位方法(program slicing based fault localization,PSFL),Zhang等[5]提出了3种动态切片技术：全预处理、无预处理和有限预处理,同时其针对Java程序设计出了一种动态切片工具Jslice；基于模型诊断的方法[6-7](model-based diagnosis,MBD)通过构建合适的程序模型同时使用逻辑推导的方式推理出故障的位置,由Abreu等[8]提出了基于程序频谱的缺陷定位技术(program spectrum based fault localization, SFL),则采用的是分析成功测试用例和失败测试用例在语句和语句块上的覆盖信息,这是目前一种比较主流的动态定位方法,在传统的SFL算法中,Wong等[9]通过修改Kulczynski系数提出了一种基于相似系数的DStar怀疑率计算公式；黄晴雁等[10]通过分析执行信息与执行结果之间的关系,提出了基于条件概率的缺陷定位方法CPStar,取得了良好的定位效果；考虑到SFL技术没有充分解析代码之间的依赖关系,文万志等[11]在缺陷定位中引入程序切片和统计学方法,随后又提出了层次切片谱,将不同的层次间的依赖关系应用与缺陷定位中,曹鹤龄等[12]则将动态切片和关联分析相结合,构建混合频谱矩阵,这两种方法使得定位的精度得到了提升,然而该过程相较于SFL算法来说中消耗了大量的时间和空间资源;宗芳芳等[13]则采用分而治之的思想,将MBD和SFL算法相结合,分别定位出函数级别和语句级别的缺陷,然而该方法的模型构建和定位方式过于复杂,在实际的应用场景中仍然有所欠缺。通过分析近些年来诸多学者的改进方法,本文提出一种基于随机森林算法的函数缺陷定位策略,通过使用机器学习算法,将该缺陷定位问题转化为分类问题,同时以各个属性在模型中的贡献度作为为函数缺陷的概率估计,实验证明,在缺陷定位到函数方面,准确度有了显著提高。

1 准备工作

针对缺陷程序,动态的传入多个测试用例从而获得各个测试用例在执行过程中的函数调用信息,将函数的执行信息进行统计作为数据集的特征,执行结果作为label,运用随机森林算法计算出各个函数的可疑度,同时生成可疑函数候选集并进行检测。

函数的调用序列是指程序在特定的输入下函数之间调用关系的全信息[14],主要提取的为函数间的调用关系以及函数之间的调用次数。

定义1成功测试用例集与失败测试用例集。假设：

T={t1,t2,…,tn}

(1)

为待测程序P的测试套件,总共有n个测试用例。对于每一个测试用例:

tj=(Ij,Oj)

(2)

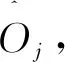
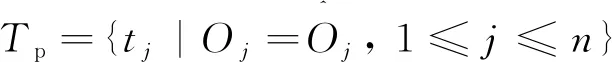
(3)

失败测试用例Tf可以表示为

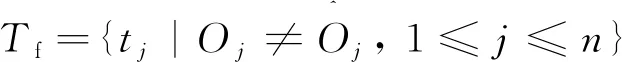
(4)

测试用例的执行结果用单位向量e表示,当tj∈Tp时,ej=0;否则当tj∈Tf时,ej=1。

定义2函数调用序列。假设程序P中的函数为M={F1,F2，…，Fm},则程序P在测试集tj上的动态函数调用序S(P,tj)为

S(P,tj)={|Fs,Fe∈M,n∈N*}

(5)

式(5)中：Fs代表调用函数；Fe表示被调用函数；n表示该序列的调用次数。

定义3二元组。将函数调用图G抽象定位为一个二元组(V,E),其中V是顶点的组合,即为各个函数的名称的集合,E为边的集合,表示函数之间的调用关系,用有序数组对(x,y)表示。

定义4邻接表。对图G中的每个定点建立一个邻接关系单链表,第i个单链表中的节点表示以Vi为起点的弧。即所有从顶点Vi出发的边所指向的节点均在该条单链表中,从而可找到任意节点出度和入度信息。

通过对于函数调用信息进行提取从而获得需要的特征,即各个函数的出度入度信息,并将该数值进行线性变换,从而形成矩阵A,其中aij表示第i个测试用例在第j个函数上的覆盖情况,所以(A,e)则是需要分析的初始数据集。

2 算法设计

在实际的生产环境中,由于缺陷函数在程序的比重较轻,由此导致测试用例在执行时正负样本不均衡,在进行模型训练时会导致结果更多的偏向正样本。采用合成少数类过采样技术[15](synthetic minority over-sampling technique,SMOTE)获取来保证样本的正负样本达到最佳比例,而后采用随机森林算法进行分类模型的训练并计算出特征重要性从而获得各个函数缺陷可疑度的排序。

2.1 SMOTE算法

针对不平衡数据集的处理通常包含代价敏感方法和采样方法[16]。然而代价敏感方法中的错误代价难以精确的估计。采样方法分为欠采样和过采样两种,其中欠采样方法通过删除部分多样本数据来使得数据达到平衡,这种方式从而导致样本的数据的丢失,所以选择过采样SMOTE方法。

SMOTE算法的主要思想是对少数类别样本进行分析,根据少数类别样本人工合成新样本添加到数据集中,具体流程如下：对于少数类样本中的每一个x,即(A,e)中的失败测试用例,以欧式距离为标准计算其到少数样本集Smin中所有样本的距离,得到其k近邻；根据样本不平衡比例设置一个采样比例确定采样倍率N,对每一个少数类样本x从其k近邻中随机选择若干个样本xn,则新样本为

xnew=x+rand(0,1)*|x-xn|

(6)

图1所示为使用SMOTE算法生成数据的效果。

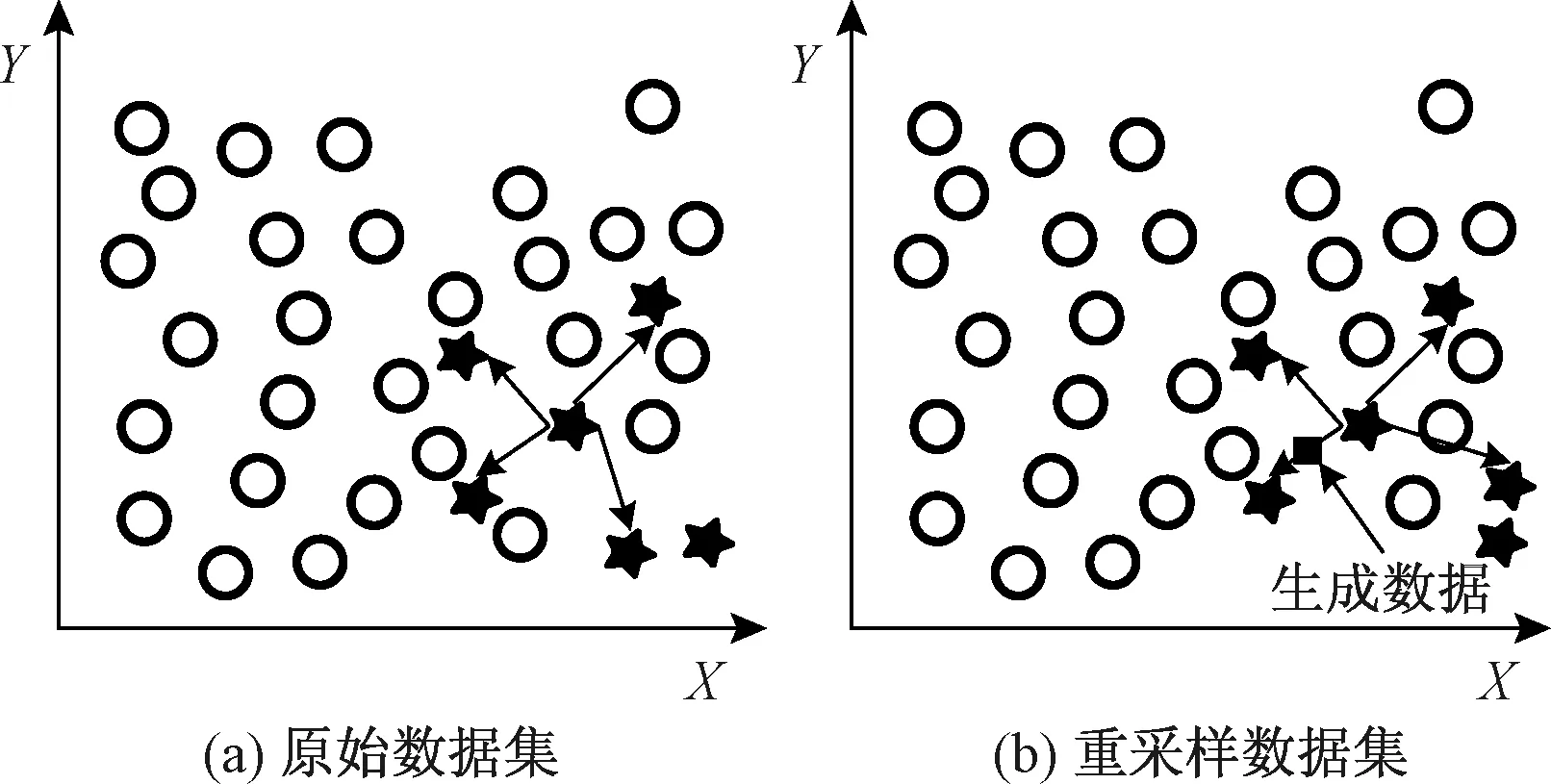
图1 数据集前后对比

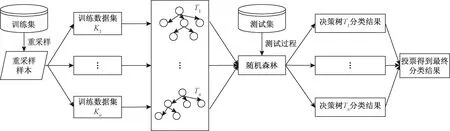
图2 RF算法流程

2.2 随机森林算法

由于不平衡的数据经过过采样变为平衡数据后,容易出先过拟合的现象,同时单个分类器存在性能提升的瓶颈问题,所以选择集成学习(ensemble learning)[17]来提高模型准确率和泛化的能力。随机森林算法[18]是一种基于决策树(decision tree, DF)的集成学习方法,解决了决策树的性能瓶颈问题,对于噪声和异常值有较好的容忍性。决策树的构造算法是分类与回归树(classification and regression tree,CART)。由函数的覆盖情况与程序的执行情况构成了初始数据集,由此将缺陷定位问题转化为了一个二分类问题。具体的算法流程如图2所示。

特征重要性反应了其对于预测结果的影响程度,由于研究问题属于一个二分类问题,所以特征重要性直接反映了其对于label属性的贡献程度——函数存在缺陷的可能性,本文的数据集属性为各个函数的调用与被调用信息,由此属性的特征重要性转化为该函数为缺陷程序的概率。

采用基于袋外数据的分类准确度来衡量每个属性的特征重要性[19]。

该算法具体步骤如下。

算法1：FDLRF算法

输入：覆盖矩阵(A,e)

输出：各个属性的特征重要性L(函数可疑序列)

(*少数类样本T,使用SMOTE算法生成样本数量N%,邻居数目k*)

步骤1 将样本进行赋值y←e,X←A,同时获得重新采用的样本X_smo,y_smo ← SMOTE(T,N,K),

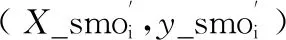
步骤3 fori=1,2,…,L

步骤3.1:从每个样本的特征维度M中选择m个特征子集,调用算法2,每次树进行分裂时,从m个特征中选择最优,构建一棵决策树Ti

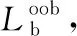
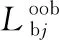
End for

步骤4 用L棵决策树对测试集X进行预测,得到

T1(X),T2(X),…，TL(X),以投票方式得到样本的类别标签

步骤5 统计计算出每个特征的特征贡献度

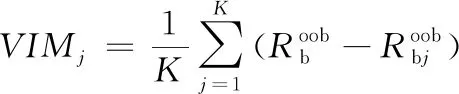
(7)

算法2：Decision Tree 生成算法

输入：覆盖矩阵(A,e)

属性集M={m1,m2,m3，…，md}

输出：一棵决策树T

步骤1 将上步中获得数据作为训练数据集D,计算现有特征的基尼指数,对每一个特征M的可能取值mi计算其在“1”,“0”下分割为D1、D2下的基尼指数

步骤2 根据特征B以及其所有可能切分点,计算出最优特征及最优切分点,由此生成两个子节点,将训练数据集进行分配

步骤3 重复算法1、算法2的步骤,直至满足停止条件为止

(*停止条件是节点中的样本个数少于预定阈值,或者样本集中的基尼系数小于预定阈值,或者没有更多特征)

步骤4 生成决策树T

3 实验分析

3.1 实验数据集

使用经典的Siemens数据集进行实验,该数据集下载地址为SIR,表1为其信息的具体介绍,包括实验对象名称、功能描述、代码行数、每个对象的错误版本数,以及测试用例的个数。实验以函数数量,代码行数最多的replace数据集为例进行论证。

通过动态运行测试用例对程序进行追踪,动态获取函数的调用序列主要使用的C语言的代码追踪工具pvtrace[14],该工具依赖于gcc编译器的hook机制,在函数的入口和出口打上“标签”从而获取“调用者”函数符号地址信息并保存到文件中,然后通过addr2line根据给定的地址从可执行文件中找出对应的“函数名”最后生成dot文件,使用graphviz展示某一测试用例执行缺陷程序时函数调用情况，如图3所示。

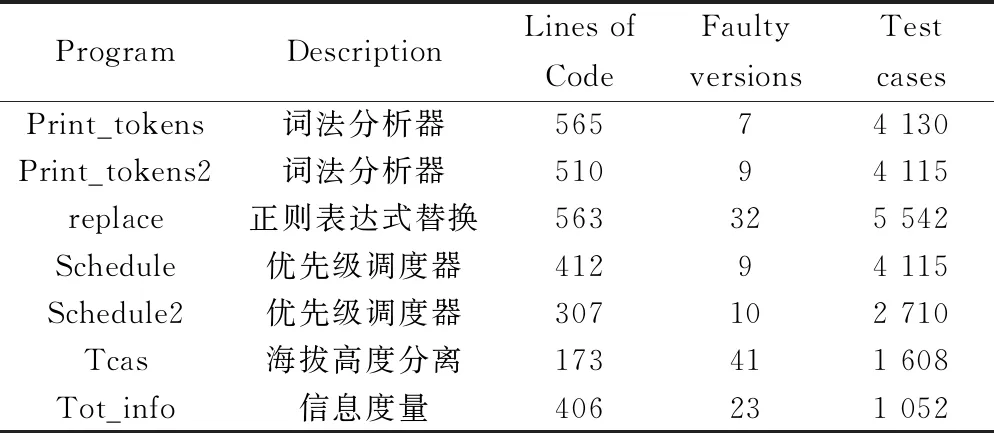
表1 西门子数据集信息

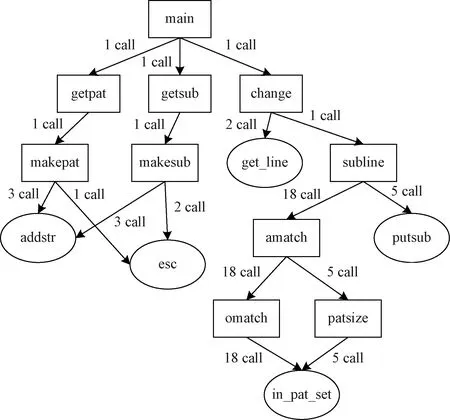
图3 函数调用图

通过分析函数在测试用例执行过程中的动态信息,以各个函数名作为特征属性,各个方法的出入度信息作为属性值,由此获得待分析的数据集部分情况，如表2所示。

表2 数据集信息

3.2 模型参数

由于不平衡样本学下旨在提高少数类样本的分类性能,选择集成学习算法——随机森林进行训练,评价指标选择在评价不平衡数据集中专用指标G-mean,其定义如下：

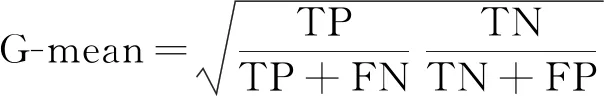
(8)

式(8)中：FN(false negative)表示被判定为负样本,事实上为正样本；FP(false positive)表示被判定为正样本,事实为负样本；TN(true negative)被判定为负样本,事实上也是负样本；TP(true positive)被判定为正样本,事实上也是证样本。

通过对SMOTE算法进行网格搜索,对采样比例进行测试,指定近邻的个数k_neighbors为5[15],随机子空间设置为10[20],在不同的比率下进行采样,由此获得最佳的采样比率为1∶8,即生成失败测试用例：成功测试用例=1∶8的数据集,如图4所示。

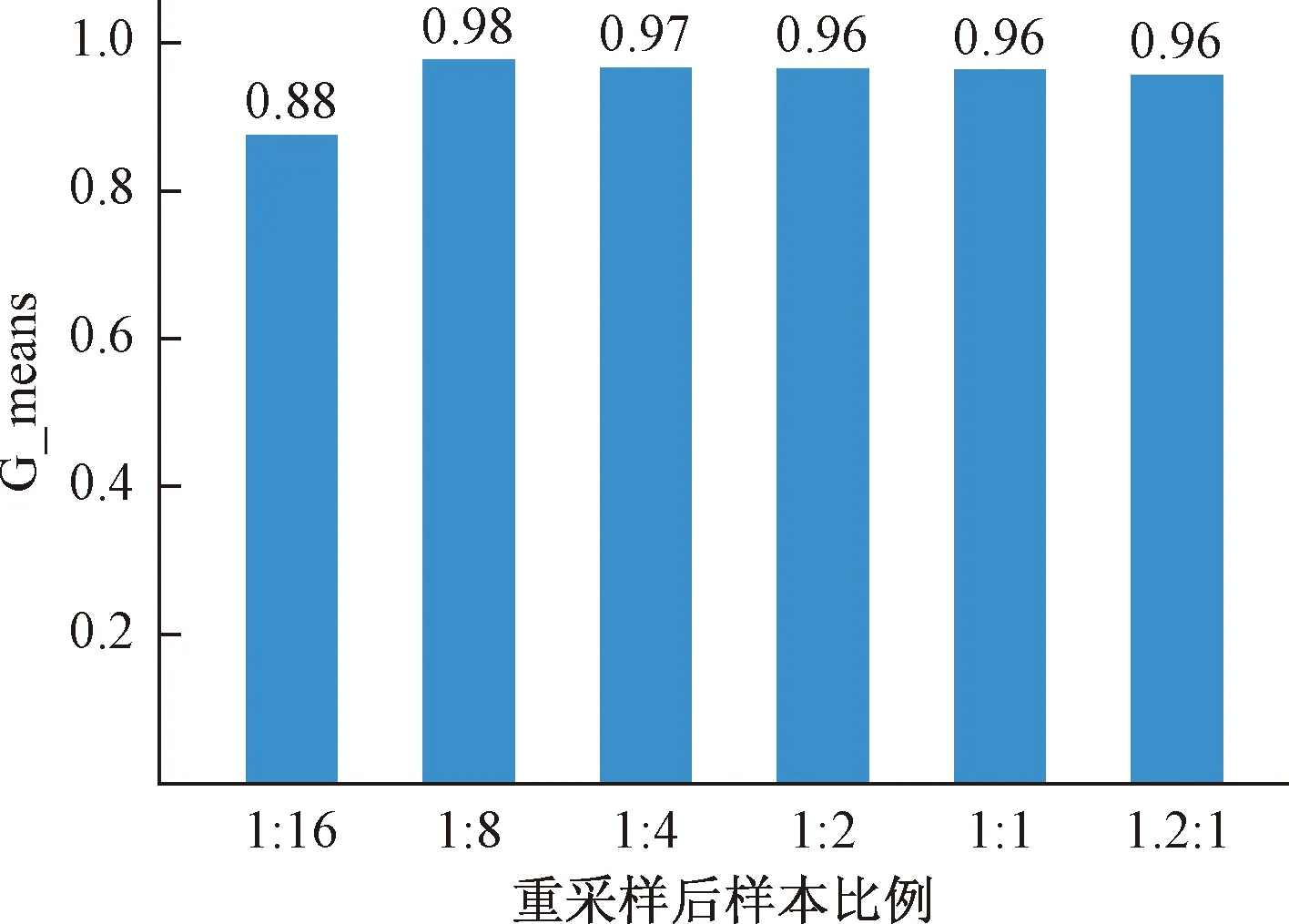
图4 不同过采样比例模型得分

RF算法中决策树的N_tree取值范围{50,100,200,500,1 000,1 500,2 000}[21]为获得分类器和过采样器的最佳效果,利用网格搜索的方式对RF进行调参,使用十次十折交叉验证的平均值作为最终性能度量结果,最终确定迭代次数为1 500次,CART树划分时的标准使用基尼指数,RF划分时最大的特征数为log2N，其中N表示该数据集的总特征数,使用袋外数据作为测试数据集,由此获得各个函数的特征重要性值,并对同名函数出入度信息做累加处理,即为该函数存在缺陷概率。

3.3 实验结果分析

由于本次实验的定位粒度为函数级别,所以本次的对比实验选择的是同样以函数为粒度进行缺陷定位的经典算法Combine、Upper[22],近年来宗芳芳等[13]提出的基于程序频谱和模型诊断的二次定位(double-times-locating,DTL)表现良好,所以将其在函数粒度上的定位也作为对比实验,同时对比自身算法不使用SMOTE算法(NO-SMOTE)的效果。

采用EXAM指标,即定位出缺陷函数需要检查的函数占总函数的百分比,作为本次实验的评价标准,实验结果如表3所示。

表3中显示了replace数据集中的31个缺陷版本的程序,通过将Combine、Upper、DTL,以及不使用SMOTE算法的FDLRE与本文算法进行对比,可以发现在29个版本(2个版本均未检测出)中均优于其他算法的工13个(灰色单元格),其中本文方法可一次定位到缺陷函数的个数为11个,占全部缺陷函数的38%；FDLRF优于Combine的共17个版本,优于Upper的共18个版本,优于DTL的共15个版本,优于NO-SMOTE的共20个版本。

对于版本中V12出现原因是,该错误并未出现在函数中,而是在全局变量的声明里,由此导致无法准确定位出缺陷的位置,版本V32出现的原因是该函数并未有故障的测试用例经过,从而无法精准定位。

对表3中的数据进行可视化处理,生成图5,同时对数据进行统计分析生成表4。在图5、表4中可以看出，除了所提出的FDLRF算法外,其他算法均出现了离群点,所有算法的EXAM最优值均为0.047 62,而在最劣值中Upper算法和FDLRF+SMOTE算法表现良好,在平均数和方差上,Upper算法优于其他3种算法。

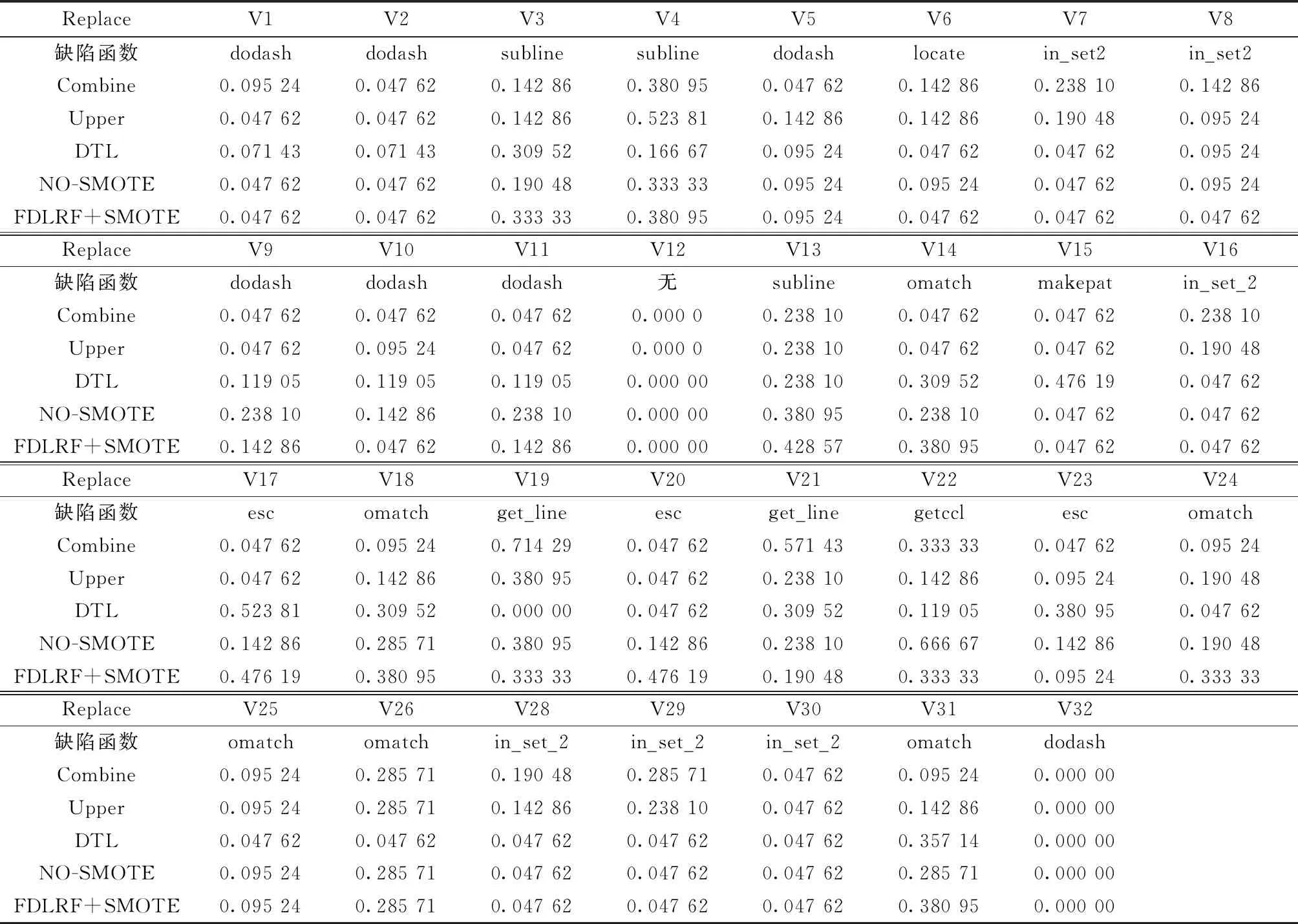
表3 定位到缺陷函数占总函数的比值

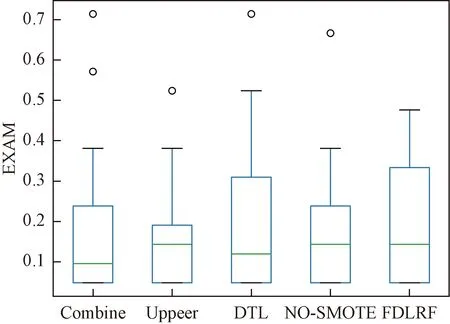
图5 缺陷定位结果比较

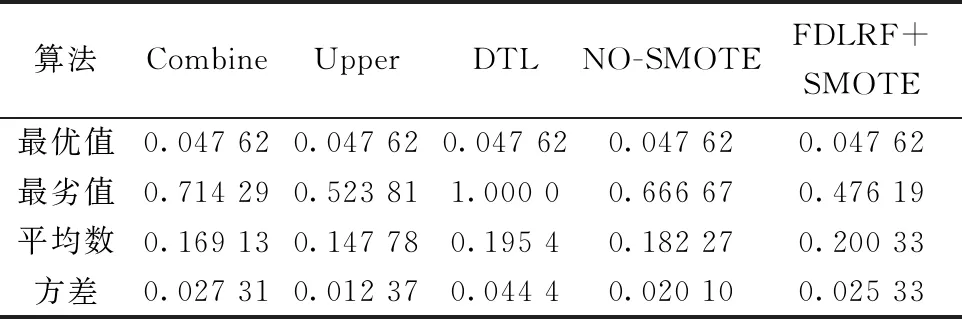
表4 统计结果对比

为了证明实验的有效性,统计每一种方法的平均有效值,将实验对象进行扩展,验证西门套件中的其他6个数据集,以实验的平均结果作为展示，如图6所示。由图6可以看出，FDLRF算法呈现出来最快的收敛速度,Upper算法次之,同时,本文方法在检测10%的代码可以定位出50%的缺陷,检测40%代码可以定位出大约90%的故障。同时可以发现,在未使用SMOTE算法时,算法的收敛速度较慢,其原因可能是正负样本不均衡,导致实验结果偏向于正向样本导致。通过以上角度的对比分析表明,本文方法有较好的表现与实用价值。

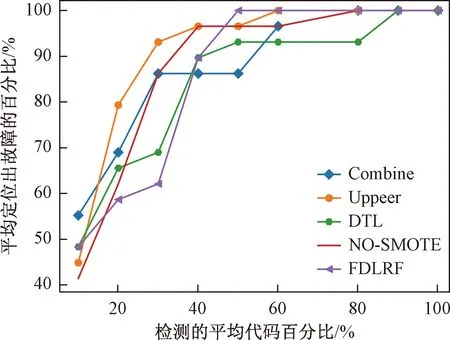
图6 不同方法有效值对比

4 结论

提出了基于随机森林算法的函数缺陷定位方法FDLRF,通过动态收集函数的调用信息,建立特征矩阵。将缺陷检测问题转化为分类问题,利用SMOTE算法对数据进行重采样从而获得均衡数据,从而使用随机森林算法对数据进行分类预测,以基尼指数作为计算特征重要性的标准,即每个属性对于label属性的贡献度,将该标准作为每个函数出现缺陷的概率从而获得函数缺陷可疑序列。通过在以EXAM作为评价标准,同时在第3节4个方面进行对比,展示了FDLRF算法的良好表现。

虽然经过研究表明本文算法有较好的定位效果,但该算法统计函数的调用的全信息,所以对于测试用例有较高的依赖性,失败测试用例覆盖信息较少,使得数据在进行分类预测结果具有倾向性,如何保证实验样本均衡同时涵盖更多的失败测试用例信息尤为重要；其次实验建立在测试用例均为正确的基础之上,这无形之中增加了局限性；最后Siemens程序包是序列化程序,在并发性程序的检测上可能面临更多的问题。