重力驱动自然对流-相变耦合散热系统数值模拟
陈 浩, 康 伟, 石秋雨, 李 强*
(1.南京理工大学能源与动力工程学院电子设备热控制工信部重点实验室, 南京 210094;2.全球能源互联网研究院有限公司先进输电技术国家重点实验室, 北京 102211)
近年来,随着电网系统的发展,低压单相用电负荷增长迅猛,由此引发的配电变压器三相负荷不平衡现象日渐突出[1]。通过使用可关断的绝缘栅双极型晶体管(insulated gate bipolar transistor, IGBT)等开关部件进行适当的触发控制,可输出幅值可调、相位角可调的电流或电压,从而实现平衡三相负荷电流和无功补偿的功能[2]。在工作过程中大功率IGBT模块会产生很大的损耗,这些损耗通常会变为废热。为防止大功率IGBT模块因为过热而损坏,需要对其进行及时有效地散热。
目前IGBT模块所在的机柜内部经常使用单相受迫对流换热技术,需要外部动力,增加了机柜内部的能耗以及维护成本。而相比采用强迫对流换热技术,自然冷却虽然可能散热效果没有强迫对流好,但是噪声小,不需要外部动力,运行稳定,因而更适用于无人值守等场合且可以有效减小能耗[3-5],由于上述优势,自然对流在很多场合得到了应用。但是对于大功率设备而言,自然对流较低的散热能力限制了其应用,因而需要采取措施增强自然对流的散热能力。目前很多研究采用安装翅片这种增大对流换热面积的方式强化自然对流的散热能力。邱燕等[6]利用数值计算的方法对自然对流条件下竖直放置的纵向翅片管的传热特性进行研究,在此基础上对竖直纵向翅片管在基管近似恒壁温条件下进行试验研究;郭建忠等[7]运用计算流体动力学(computational fluid dynamics, CFD)方法对汽车管带式百叶窗散热器进行性能分析及翅片结构优化,研究表明百叶窗翅片结构中综合性能最佳的翅片结构是间距2.4 mm,开窗角度27°;赵俊志等[8]研究了一种自然对流条件下竖直放置对称阵列斜翅热沉的换热性能,分析了翅片高度、纵向间距对换热性能的影响,讨论了对称阵列斜翅热沉换热特点;Castell等[9]通过实验研究了具有垂直翅片的圆柱形模块的表面自然对流换热系数,给出了 不同翅片的传热系数随温差的变化规律;Elshafei[10]通过实验研究了翅片散热器的自然对流换热特性,考察了其几何尺寸、热流密度和方向对换热特性的影响;Ahmadi等[11]对垂直安装的矩形间断翅片的稳态自然对流换热进行了数值和实验研究,研究结果表明增加中断垂直安装的矩形鳍片可以大大提高热性能,并存在一个最佳的翅片中断。
安装翅片的自然对流散热器虽然可以通过增大散热面积提升其散热能力,但是由于其传热能力的限制,热源处的热量不能有效地传递至距离热源较远的区域,从而造成散热器表面温差增大及散热效率的下降。因为工质相变时温度均匀一致且传热系数较高,具有高导热性和良好的均温性,因而可以利用工质的相变换热增强散热器的传热能力。目前相变换热技术如平板热管[12-14]、脉动热管[15]、环路热管[16-19]、重力热管[20-22]等得到了广泛的应用。莫冬传等[12]制造了高热流密度传热组件——均温板,并对其传热特性进行了研究,实验表明该均温板可承受非常高的热流密度且具有良好的均温和散热特性;Liu等[13]对一种基于叶脉系统的新型均温板进行了性能测试,当叶脉网络分形角为40°和50°时,均温板的热阻较小,矩形均温板的热阻约为0.06 ℃/W;寇志海等[14]对一种以微槽道作为吸液芯的平板式热管散热器的传热特性进行了实验研究,分析了加热功率、冷却强度、工作倾角等因素对该平板热管散热器传热性能的影响规律;张东伟等[15]综述了热管结构和工质对脉动热管强化换热的影响,整理了脉动热管理论研究和数值模拟的最近研究进展,给出了当前亟需解决的关键问题,为脉动热管技术后续研究提供了借鉴思路和方向;黄洁等[16]对阿尔法磁谱仪低温冷却器环路热管的启动特性进行了数值模拟研究,结果表明热负荷高利于环路热管的启动;吕虓等[17]设计开发了一套平板式环路热管,比较了2 mm×1.5 mm和1 mm×1 mm(高×宽)两种蒸气槽道环路热管在不同倾角和充液率下的性能,结果表明两种蒸气槽道在相同条件下最低启动功率相同,但前者启动时间和过渡时间较后者短;Pastukhov等[18]介绍了氨回路热管(lopp heat pipe, LHP)的研制和实验研究结果,该热管用于同时冷却多个散热量可变的热源,研究结果表明液体管线上的热作用对主热源的温度有相当大的影响,而蒸汽管线上的热作用对主热源的温度没有影响;Gabsi等[19]对稳态运行的带平板蒸发器的铜水环热管的热性能进行了数值模拟,通过参数化研究给出了液体和蒸汽管道的半径和长度、冷凝器的长度、散热器温度和传热系数等不同的关键参数的影响;王淑彦等[20]研究了井筒重力热管的传热性能和工作过程,进而改进和优化重力热管的传热性能,建立了重力热管内部流动和传热的数学模型。利用该模型对重力热管的传热特性进行了数值模拟,得到了热管正常工作时,液膜厚度、蒸汽流速和液膜流速及热管换热系数随热管高度的变化规律;付秋刚等[21]研究了重力场中不同吸液芯微热管的传热性能,选用了沟槽式和烧结式两种吸液芯的热管为研究对象,实验测量了两者在不同重力倾角时的温差、热阻和极限功率;Zhang等[22-23]从概念、理论及实验3个方面研究了分离式重力辅助热管,建立了包含质量连续性、能量守恒和达西方程的稳态热模型。对于应用于大功率设备的散热系统而言,可以采用相变换热技术将热源处的热量有效均匀地传递至具有翅片的散热系统表面,从而增大系统的散热效率。
综上所述,针对大功率设备的散热需求,通过自然对流散热和相变换热耦合,设计研究了重力驱动的自然对流-相变耦合散热系统并建立物理模型,对系统内部的流动与传热过程进行数值模拟分析,研究充液率、加热功率对系统散热性能的影响。
1 散热系统设计计算
重力驱动自然对流-相变耦合散热系统结构示意图如图1所示,蒸发板内部液体工质吸收废热发生相变,产生的蒸汽通过管路进入冷凝板冷凝为液体工质并释放热量,热量通过冷凝板的基板和翅片释放到环境中,液体工质在重力作用下通过管路流经储液器回流到蒸发板中,从而完成一个循环。

图1 系统结构示意图
为了设备安全可靠地工作,在有限空间内能够及时有效地将热源热量传递到周围环境中,需要进行散热计算设计合适尺寸的散热系统。根据设备工作时产生的损耗功率Q、器件结温Tj以及环境温度Ta,计算散热系统尺寸参数并根据需求选择合适尺寸的散热系统。
根据热源功率、IGBT结温、结壳以及壳体与蒸发板之间的热阻,可计算得到蒸发板外表面温度为
Tplate,o=Tj-ΔT=Tj-QR
(1)
式(1)中:Tj为IGBT结温,K;Q为热源功率,W;R为电子芯片到蒸发板之间的总热阻, K/W。
根据蒸发板的尺寸可得蒸发板内表面温度为
(2)
式(2)中:Te,o为蒸发板壳体外表面温度, K;Le为蒸发板壁面厚度, m;ke为蒸发板壳体热导率, W/(m·K);Ae为蒸发板与热源之间传热面积, m2。
当液体温度升至饱和温度以上时,工质会发生相变。设计中基于核态沸腾的假设进行设计计算,沸腾换热系数可用下式联立计算[24]:
(3)
q=hb(Tplate,i-Tsat)=hbΔTe
(4)
式中:q为热流密度, W/m2;μl为液体动力黏度,Pa·s;hfg为工质潜热, J/kg;g为重力加速度, N/kg;ρl、ρv分别为液体和气体密度, kg/m3;σ为表面张力, N/m;cp,l为液体定压比热容, J/(kg·K); ΔTe为过余温度, K;Prl为液体普朗特数,hb为沸腾换热系数, W/(m2·K);Tsat为工质饱和温度, K。
当蒸汽温度降至饱和温度以下时,就会发生凝结。设计中基于膜状凝结的假设进行设计计算。无论层流还是湍流,平均冷凝换热系数均可采用以下关系式[24]:
(5)
对于式(5)中的Re,可用下列各式计算[24]:
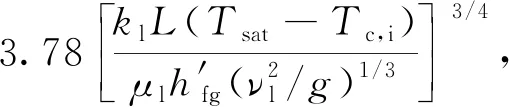
Re≤30
(6)

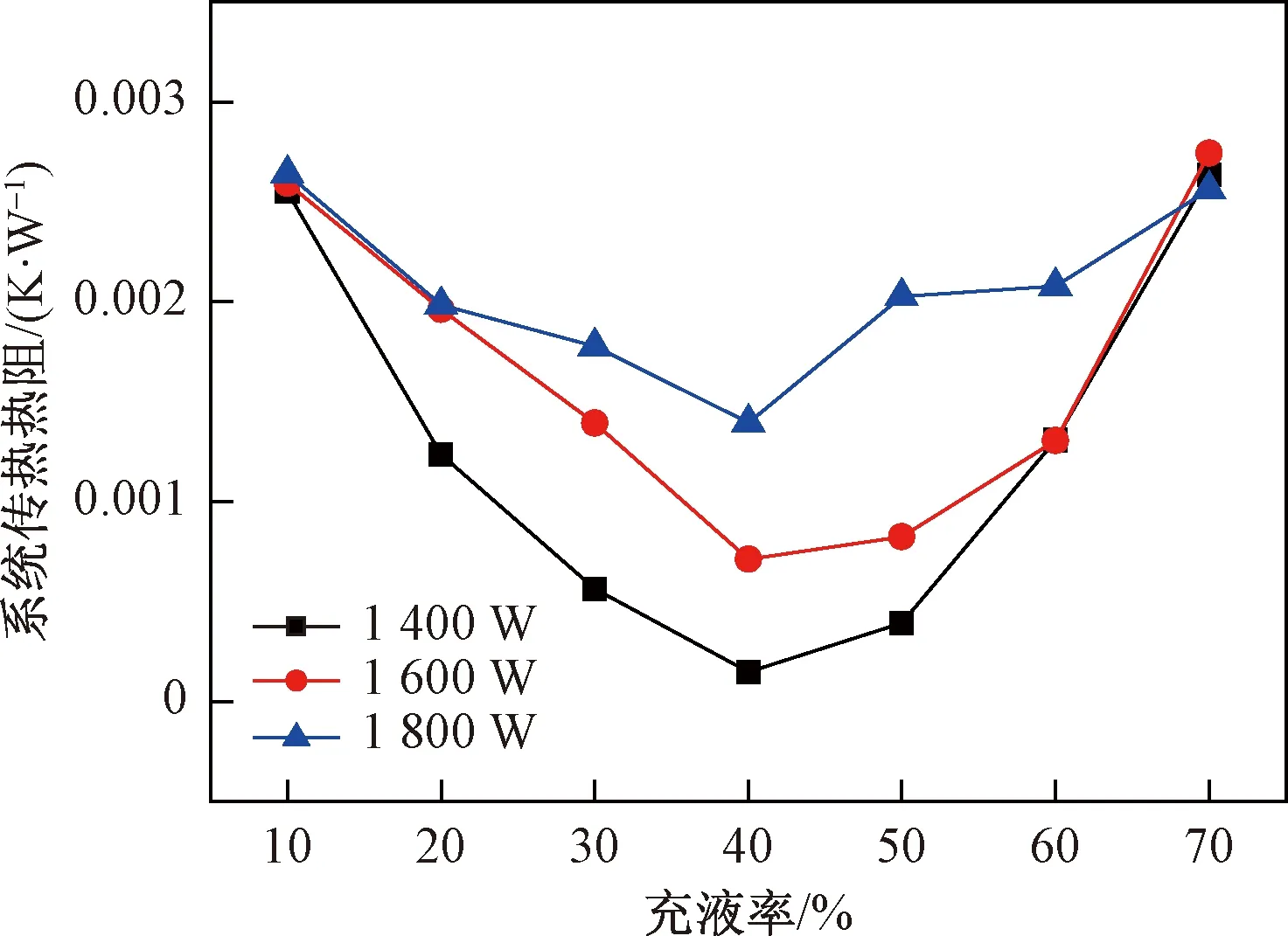
30 (7) Re≥1 800 (8) 式中:kl为液体热导率, W/(m·K);νl为液体运动黏度, m2/s; 修正潜热用下式计算[24]: h′fg=hfg(1+0.68Ja) (9) (10) 式中:Ja为雅各布数。 根据式(1)~式(10)联立可计算得到冷凝基板内表面温度,而冷凝基板外表面温度为 (11) 式(11)中:Lc为冷凝基板壁面厚度,m;kc为冷凝基板热导率, W/(m·K);Ac为冷凝基板传热面积, m2。 假定环境温度T∞为40 ℃,因而空气定性温度Tm的计算式为 (12) 冷凝板外表面安装翅片以增大自然对流换热面积,翅片的尺寸对散热系统与环境之间的热交换具有重要影响,因而需要对翅片尺寸进行优化计算,从而得到最佳尺寸参数。要计算冷凝板的对流换热速率,需要先计算冷凝板表面的自然对流换热系数。而在计算之前需要先判断自然对流边界层为层流还是湍流,自然对流边界层中的过渡与流体中的浮力与黏性力的相对大小有关,习惯上用瑞利数表示过渡发生的条件,临界瑞利数为[24] (13) 式(13)中:β为热膨胀系数,1/K;α为热扩散系数,m2/s。 因此可以计算冷凝板在最大尺寸下的瑞利数[24]: (14) 式(14)中:Grc,s为格拉晓夫数;νa为空气运动黏度, m2/s;αa为空气热扩散系数, m2/s;Lc,s为冷凝基板长度, m;β[24]为 (15) 多个翅片与基板组合的冷凝板,每两个翅片与基板形成一个类似槽道的结构,对于此结构表面的对流换热系数计算,欧伦巴斯得到了以下的半经验关系式[24]: (16) 式(16)中:Sf为翅片间距, m;Lf为翅片长度, m; 平均努塞尔数和瑞利数的定义分别为[24] (17) (18) 式中:ka为空气热导率, W/(m·K)。 翅片表面温度取翅片中间部分的温度值,翅片效率[24]为 (19) 式(19)中:H为翅片高度, m;m[24]为 (20) 式(20)中:kf为翅片热导率, W/(m·K);δ为翅片厚度, m。 因而计算翅片表面系数时所取温度为 Tfin,m=T+ηf(Tfb-T) (21) 式(21)中:Tfb为翅根处温度, K。 冷凝板无肋表面对流换热系数可根据垂直平板表面自然对流换热公式计算[24]: (22) (23) 式中:Pra为空气普朗特数。 图2 翅片间距及厚度对散热量的影响 根据式(11)~式(23)可以计算得出翅片间距对系统散热量的影响如图2所示。由图2可以看出,翅片越厚,散热量越大,这是因为翅片效率随着厚度增加而增大;散热量随着翅片间距的增大先增大后减小,在相同空间下,随着间距的增大,翅片个数会减小,因而存在一个最优值,使得散热量达到最大,由图2可以看出翅片间距在15 mm时散热量达到最大。 通过优化计算设计散热系统,蒸发板为铜材质,内部具有微槽道结构,可以增强工质的相变剧烈程度从而加强换热,同时蒸发板内部有阵列分布的加强柱,可以增强蒸发板的结构强度,减小工作时的形变量,其结构如图3所示。蒸发板尺寸为300 mm×200 mm×6.5 mm,壁厚2 mm,微槽道宽0.5 mm,深1.5 mm,槽道间距5 mm,加强柱直径为3 mm,高度为1 mm。冷凝板为铝材质,内部具有30根平行流道,入口横管为渐缩管,可以使得流量均匀分配到每根平行流道中,其结构如图4所示,冷凝板基板尺寸为2 200 mm×800 mm×10 mm,平行流道长2 010 mm,宽10 mm,深5 mm,基板表面安装有根平行翅片,翅片长2 160 mm,高250 mm,厚1 mm。 图3 蒸发板结构示意图 图4 冷凝板结构示意图 通过系统最高温度和系统传热热阻等参数衡量系统散热性能。蒸发板传热热阻为 (24) 系统传热热阻为 (25) 对系统内部的流动及传热行为进行模拟研究,图1、图3和图4所示基板、翅片等为固体区域,内部工质为流体区域,为了减小计算量,只计算一块蒸发板和一侧冷凝板及翅片。系统工作时内部工质处于两相状态,具有复杂的气液两相转换过程,通过相界面发生质能传递。流体体积分数(volume of fluid, VOF)模型通过求解单独的动量方程和处理穿过区域的每一流体的容积比来模拟两种不能混合的流体,其中就包括了气液界面的稳态和瞬态处理。选择VOF模型对工质的两相行为进行模拟。 (26) (27) 式中:Sv、Sl为质量源的质量传递;αl、αv分别为气相和液相的体积组分,αv+αl=1,即气液相的体积和为1。 (28) 式(28)中:p为压力, Pa;μ为动力黏度, Pa·s;ρ和μ取决于相的属性及其所对应的体积分数。 (29) 式(29)中:keff为有效热导率, W/(m·K);Sh为能量源项, W/m3;T为温度, K;E为模型内部能量, J/kg, 可表示为 (30) 式(30)中:Ev和El分别可表示为 Ev=Cp,v(T-Tsat) (31) El=Cp,l(T-Tsat) (32) 固体区域能量方程为 (33) 式中:h为显焓,J/kg;k为固体导热系数, W/(m·K);q为热流密度, W/m2。 流道存在蒸发冷凝过程,结合流动过程中的气液变化过程,相变模型方程[25]可表示为 (34) (35) (36) (37) 式中:Sv和Sl为质量源项, kg/(m3·s);r为反映相变换热强度的因子, 1/s。 图5 单个器件内部热源分布 热源分布如图5所示,定义蒸发板下表面为非均匀分布多热源接触面,系统每块蒸发板上均匀分布6块此器件,单个器件总功率为324.6 W时各部分热源(P1~P12)功率及热流密度如表1所示,在热源加热总功率变化时,各部分热源功率也随之变化。冷凝板基板表面以及翅片片表面和环境进行自然对流换热,环境温度为40 ℃,冷凝板外部不同表面自然对流换热系数可根据式(11)~式(20)计算得到。初始状态下,系统温度为40 ℃,内部工质静止且气液分层处于饱和状态,系统内部压力为工质处于40 ℃时的饱和压力。 表1 单个器件内部热源功率及热流密度 对自然对流-相变耦合散热系统进行模拟分析,工质为R245fa,通过系统内部工质相变过程研究其传热机理,分析加热功率、充液率对其散热性能的影响。 图6 蒸发板温度云图 图6给出了系统在充液率为40%时,单个蒸发板在加热功率为1 400、1 600、1 800 W工况下的温度云图。从图6中可以看出,每块蒸发板上加载6个相同模块,每个模块内部具有不同热流密度的单元。蒸发板左下角温度最低,因为此处为蒸发板工质入口,由温度分布云图可以看出蒸发板内部工质由左下角流入,右上角流出。与图5相结合,可以看出P8、P9、P10处温度最高,这是因为P8、P9、P10热流密度较高。从表1可以看出,P1、P5、P6处热流密度也很高,但是温度要低于P10等热源,这是因为P1、P5、P6处热源更接近工质入口处,与P10等热源相比,与之进行热交换的工质温度更低。图6(a)、图6(b)、图6(c)显示,加热功率越大,蒸发板温度越高。 图7给出了单板加热功率1 800 W、系统充液率40%时启动阶段蒸发板内部两相工质的体积分布云图,蓝色表示仅存在液体工质(体积分数为0),红色表示仅存在气体工质(体积分数为1)。在初始阶段,蒸发板内部被液体工质充满,随着热量的输入,内部工质开始发生相变,有气体工质生成。从云图分布可以看出蒸发板内部很快发生相变,这表明散热系统启动很迅速,这是因为蒸发板内部具有微槽道结构,可以增强工质与蒸发板之间的热交换。随着加热的进行,液体工质的连续蒸发导致液体体积分数的减少和气体体积分数的增加。在液体蒸发的位置形成气泡,并向蒸发板顶部及蒸发板出口处流动。 按照上述过程,蒸发板内部产生的蒸汽在浮力作用下通过管路进入冷凝板进行冷凝,冷凝管路中两相工质体积分数分布云图如图8所示,图8中仅给出了截取的部分冷凝管路中的工质体积分数的分布情况。从5 s的云图可以看出,气体管路中已经开始有冷凝现象出现。随着冷凝过程的继续进行,可以看出气液界面发生很明显的波动,这是因为流动进入的气体工质对气液界面产生压力,造成了界面的波动。由15 s的云图可以看出,左侧的管路气液界面开始大幅下降,这表明有大量的气体工质开始进入冷凝板进行冷凝。在冷凝管路中冷凝后的液体工质在重力作用下通过储液器回流到蒸发板,从而完成一个循环。由图7和图8也可以证实系统内部气液相变循环过程的顺利进行。此外,从图7和图8体积分布云图中可以观察到系统内部出现了间歇沸腾的现象。 图7 启动阶段蒸发板内部两相工质体积分布 图8 启动阶段冷凝板内部两相工质体积分布 图9给出了系统最高温度随充液率的变化情况,从图9中可以清楚看出,不同加热功率下系统最高温度随着充液率的变化趋势一致,都是先减小后增大,这是因为充液率较低时系统内部参与相变热交换的工质不够,而充液率较大时,冷凝板内部冷凝区面积大大减小,工质不能与冷凝基板进行充分热交换,从而导致回流到蒸发板的工质温度增高,系统最高温度也随之增大。在同样充液率工况下,蒸发板加热功率越高,系统最高温度越大;系统充液率在40%时,系统最高温度达到最小值,单板加热功率分别为1 400、1 600、1 800 W时,系统最高温度为340.18、345.25、350.24 K。 图9 不同充液率下系统最高温度 图10 不同充液率下蒸发板平均温度 系统蒸发板平均温度随充液率的变化情况如图10所示。不同功率下的曲线变化趋势也是一致的,随着充液率的增加,蒸发板平均温度先减小后增大。和系统最高温度变化趋势一样,在充液率为40%时蒸发板平均温度达到最小值,因为在此最佳充液率下,蒸发板吸收的热量能够更有效地被传递至冷凝板处。在不同充液率下,蒸发板平均温度在加热功率为3 600 W时是最大的。充液率为40%时,蒸发板平均温度在单板加热功率为1 400、1 600、1 800 W工况下分别为325.59、327.58、329.64 K。 图11给出了蒸发板传热热阻随充液率变化情况,蒸发板传热热阻由式(24)计算。不同功率下蒸发板传热热阻呈现相同的变化趋势,都是先减小后增大,曲线趋势可以明显地表示出蒸发板传热热阻在充液率为40%时达到最小值。单板加热功率分别为1 400、1 600、1 800 W时,蒸发板传热热阻为1.03×10-2、1.11×10-2、1.19×10-2K/W,差别不大,这是因为蒸发板内部具有微槽道结构,可以强化内部换热,从而减小了加热功率对蒸发板传热热阻的影响。 图11 不同充液率下蒸发板传热热阻 图12 不同充液率下系统传热热阻 图12给出了系统传热热阻在不同充液率下的变化情况,这也是衡量系统性能的重要参考之一。同样的,在不同加热功率下系统传热热阻均在充液率为40%时达到了最小值,在充液率较低时,没有足够的工质将热量传递至冷凝板,而在充液率较高时,冷凝板内部进行冷凝相变的区域大大减小,工质不能与冷凝板进行充分的热交换,因而系统传热热阻随着充液率的变化呈现了先减小后增大的趋势。在单板加热功率分别为1 400、1 600、1 800 W时,系统传热热阻分别为1.5×10-4、7.13×10-4、1.39×10-3K/W。而从图12中也可以看出,在相同充液率下,加热功率越大,系统传热热阻越大,从式(25)可以得知,随着加热功率的增大,蒸发板与冷凝板之间的平均温度差增长幅度越来越大。 设计了一种重力驱动的自然对流-相变耦合散热系统,使用R245fa作为工质,采用VOF模型模拟系统内部两相流动及传热过程,分析充液率及加热功率对系统性能的影响,得到以下结论。 (1)对于大功率电力设备中的非均匀分布热源,热量能够通过工质相变从热源处有效传输到冷凝板,并通过冷凝基板及翅片释放到周围环境中,这表明该系统能够对其进行及时有效的散热,因而研究成果可以为以后大功率电力设备散热系统的设计提供参考。 (2)随着充液率的增加,系统最高温度、蒸发板平均温度、蒸发板传热热阻以及系统传热热阻均呈现先减小后增大的趋势,系统存在着最佳充液率,在最佳充液率40%工况下,系统传热及散热性能达到最佳。 (3)加热功率同样对系统传热及散热性能产生重要的影响,加热功率越大,系统最高温度、蒸发板平均温度以及系统传热热阻也越大,而蒸发板内部微槽道结构的存在减小了加热功率对蒸发板传热热阻的影响。 (4)蒸发板和冷凝板内部工质能够快速发生相变,这表明系统在热量输入后能够迅速启动,传输并释放热源处的废热。该系统内部工质流动可观察到间歇沸腾的现象。





2 理论模型
2.1 连续性方程
2.2 动量方程
2.3 能量方程

2.4 相变模型
2.5 边界条件


3 结果分析






4 结论

