非线性(时滞)动力学问题的一种新暂态时程积分解法
颜廷浩, 任传波, 周继磊, 吴凯伟, 曹军帅, 孙志钏
(山东理工大学交通与车辆工程学院, 淄博 255000)
在时域中,数值解法可直观地确定非线性系统的运动状态(位移、速度、加速度)与系统参数和初始条件的关系,对于线性和非线性系统,已提出大量数值计算方法[1-4]。对于一般的动力学系统,其动力学微分方程可以写为时间离散化的方程形式,这种方程的数值解越来越受到关注。
时程积分方法能够有效地求解微分方程的数值解,Subbaraj等[5]和Dokainish等[6]研究了直接时程积分在结构动力学系统中的显式和隐式计算方法,证明这种逐步积分方法是一种强有力的计算手段。Katsikadelis[7]提出了一种直接时间积分方法,用于求解结构线性和非线性多自由度系统动态响应的运动方程。Chen等[8]对非线性结构直接积分算法的稳定性进行了相关的研究。Keierleber等[9]研究了高阶隐式动态时间积分方法。Zuijlen等[10]研究了结构动力学和流固耦合计算的显式和隐式高阶时间积分。为提高时间积分求解方法的精度,钟万勰[11-12]提出暂态历程的精细计算方法,以其高精度、无条件稳定等优点得到了广泛的应用。对于线性定常结构动力系统,精细积分法可以得到逼近于精确解的数值结果。在此基础上,王立峰等[13]研究了求解非齐次线性常微分方程的精细积分方法。张庆云等[14]研究了一种提高增维精细积分法计算精度的方法。顾元宪等[15]、张靖姝等[16]、任传波等[17]研究了非齐次动力方程,刚柔耦合系统和结构动力学系统等问题。
时滞在各类系统中广泛存在,甚至不可避免,包含时滞的系统可以用时滞动力学微分方程来表示。Bellen等[18]通过一种均匀修正的隐式Runge-Kutta方法计算了时滞微分方程数值解。Shakeri等[19]通过同伦摄动法求解了时滞微分方程,算例显示该方法可以取得令人满意的效果。包含时滞的非线性系统越来越多地被研究,这类问题可以利用非线性微分方程的近似解析法来计算。实际研究中,主要利用MATLAB中函数对时滞动力学微分方程进行数值求解。
现提出一种求解非线性微分方程的新暂态时程积分方法。在此基础上,对包含时滞的非线性动力学微分方程进行了数值求解研究。在暂态时程积分过程中,将非线性项看作非齐次项,在瞬态区间起始时刻处进行Taylor展开并结合Romberg数值积分进行计算。Taylor展开时,将系统状态方程连续引入到非线性项导数的求解过程中,来计算高阶导数。对于含有时滞的非线性微分方程,将时滞项同样看作非齐次项,通过分析时滞项暂态时程积分的上下限来确定时滞项的值。暂态时间内未知的时滞项数值利用线性插值进行计算,然后通过 Romberg 积分求得时滞积分项的数值。以强非线性振子方程为例,研究新暂态时程积分方法求解强非线性微分方程的有效性和精确度,又以包含时滞的Duffing方程和van der pol方程为例,研究新暂态时程积分方法对含有时滞的非线性微分方程的求解效果。
1 非线性动力学问题的暂态时程积分解法
对于一般的非线性问题可由以下微分方程表示:

(1)


(2)
式(2)中:H、A、B是与M、C、K有关的常系数矩阵。将式(2)右侧外力项和非线性项均视为非齐次项,根据常微分方程理论,式(2)有一般解:

s)]{AF(s)+Bf[s,y(s)]}ds
(3)
取步长为Δt=tk+1-tk,对式(3)进行离散得:

s)]{AF(s)+Bf[s,y(s)]}ds=


s)]Bf[s,y(s)]ds
(4)
式(4)可写为

(5)
式(5)中:
T=exp(HΔt)
(6)

(7)

(8)
对于式(4)右端的第1项中T可以根据文献[12]方法精细得出,式(4)右侧的第2项可以根据文献[17]方法精细得出。
对于式(4)右侧第3项通过Romberg积分方法求解得,由文献[20]可知Romberg积分格式为

m=1,2,3…
(9)
其中:

(10)

(11)
式(9)中m的取值要视问题的求解精度而定,m的取值越大精度越高。本文中取m=2进行计算。
根据式(9)~式(11)所给格式,对式(4)中第3项进行计算,步骤如下:

(12)

tk+Δt时刻所对应的y值。

离散方程(3)的时间步长为Δt,在时间段[tk,tk+1]中,tk时刻所对应的f[tk,y(tk)]已知,因此可对非线性项f(t,y)在tk处进行泰勒展开,以求得时间段内非线性项的未知值f[tk+1/4,y(tk+1/4)]、f[tk+1/2,y(tk+1/2)]、f[tk+3/4,y(tk+3/4)]、f[tk+1,y(tk+1)]。
泰勒展开的形式如式(13)所示,展开阶次为4阶。

(13)
式(13)中:

(14)

将非线性系统状态方程(2)代入到式(14)中,则式(14)中的各高阶导数项可写为如下形式的方程:

(15)
通过重复将系统状态方程代入到式(15)中,高阶导数被有效地降阶。当求得Taylor展开式(13)中的系数D、E、F后,利用该式即可求得时间段[tk,tk+1]中未知时刻的非线性项值,如式(16)所示。

(16)
将式(16)所得系统状态值代入Romberg积分式(12)中,则非线性项得解。利用逐步递推的暂态时积公式(4),则可求得非线性微分式(1)时域内的数值解。
下面求解三次强非线性振子方程。三次强非线性振子方程形式为

(17)
式(17)中的参数分别取为:a=1.5,b=3。


(18)

图1 4阶Runge-Kutta法和新暂态积分法求解强非线性振子方程的结果对比
对于非线性项f=-ay13-bsiny1,按照式(13)~式(14)在t=tk处进行Taylor展开,结果如下:

(19)
将式(19)代入式(16)中,则时间区间[tk,tk+1]内未知值f[tk+1/4,y(tk+1/4)]、f[tk+1/2,y(tk+1/2)]、f[tk+3/4,y(tk+3/4)]、f[tk+1,y(tk+1)]得求,利用Romberg积分式(12),可求得非线性项的值,通过逐步递推积分式(4),即可求得强非线性振子式(17)时域内的数值解。
利用上述方法对式(17)进行求解,仿真时长为50 s。作为对比,选择4阶Runge-Kutta法求解式(17),结果如图1所示。由图1可知,新暂态时程积分法可以有效求得非线性微分方程的数值解。时间步长相同时,暂态时程积分法和4阶Runge-Kutte法可以取得相近的结果,如表1所示,误差量级在10-3左右,这证明了暂态时程积分解法的有效性。

表1 新暂态时程积分法(ITTI)和Runge-Kutta法的结果和误差
2 含时滞的非线性动力学问题的暂态时程积分解法
对于一般包含时滞的结构动力学系统,可以用以下动力学微分方程表示为

(20)
暂态时程积分法宜于处理一阶方程,因此将式(20)写为状态方程形式为
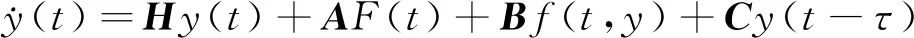
(21)
式(21)中:H、A、B是与M、C、K有关的常系数矩阵。将式(17)右侧后3项均看作非齐次项,根据常微分理论,式(21)有一般解:

{AF(s)+Bf[s,y(s)]+Cy(s-τ)}ds
(22)
取时间步长Δt=tk+1-tk,对式(18)进行离散,即

s)]{AF(s)+Bf[s,y(s)]+
Cy(s-τ)}ds=exp(HΔt)yk+



(23)
式(23)右侧前3项根据上文方法可解,时滞项采用第一部分式(9)~式(12)所给Romberg积分进行求解。
Romberg积分需要求解的方程为

(24)

进行式(12)的计算时,[tk,tk+1]时间区间内时刻
所对应的y(s-τ)值可由线性插值法计算。

(25)
则通过Romberg积分式(9)~式(12),方程中的时滞项得解,然后利用式(19)逐步递推的积分公式即可求得含时滞非线性微分方程的数值解。
2.1 求解包含阻尼时滞扰动项的Duffing方程
包含阻尼时滞扰动项的Duffing方程可以描述为

(26)


(27)
对非线性项f=-cy13进行Taylor展开可得

(28)
通过式(9)~式(16)即可求得暂态时程积分过程中每一步内非线性项的暂态时程积分值。
式(26)~式(28)中参数值分别为:a=0.04,b=-0.2,c=0.53,A=0.4,ω=0.32,g为时滞项增益系数,τ为时滞量。
当阻尼时滞扰动项参数分别为g=-1.51 N/m,τ=1.325 s时。时滞积分项中:当tk<1.325 s,y2(t-τ)|tk=0,当tk≥1.325 s时y2(t-τ)|tk=y2(tk-13 250),其中
250。
通过线性插值式(24)、式(25)和Romberg积分式(9)~式(12)即可求得暂态时程积分中每一步中时滞项的积分值。
利用逐步递推的暂态时程积分式(23),即可解得含时滞的非线性微分方程的时域数值解。
利用MATLAB中时滞微分方程求解函数和本文方法分别对方程进行计算,可得结果如图2所示。

时滞扰动项参数为:g=-1.51 N/m,τ=1.325 s
当阻尼时滞扰动项参数为g=-1.51 N/m,τ=0.5 s时,可得结果如图3所示。
观察仿真结果图3可得,本文方法解得结果和MATLAB所解结果除开始几秒钟存在差异外,其余仿真结果几乎一样,MATLAB所绘制仿真图像有明显的转折点,本文解法所绘制图像更为连续光滑。当仿真时间为150 s,MATLAB所解数值结果共有 3 674 个,并且步长是不均匀的。本文方法时间步长为0.000 1 s,因此150 s仿真时间内共有150万个仿真结果点。由于本文方法是一种逐步递推的暂态时程积分方法,当仿真时长较长时的结果与MATLAB结果相同时,足以说明本文方法的正确性以及仿真时长较短时结果的精确性。因此两种方法仿真初始时的差异可以归结为二者的步长不同,本文方法更为精细,因此可以表现出MATLAB所没有表现的振动特征。
2.2 求解包含阻尼时滞作用的Van Der Pol受迫振动系统
Van Der Pol方程揭示了由于系统受到非线性阻尼作用而导致系统出现孤立周期振荡行为。包含阻尼时滞作用的Van Der Pol受迫振动系统,可由以下方程表示:

(29)


(30)
式(29)、式(30)中的参数值分别为:a=5,b=1,c=1,A=5,ω=2.466,g=3.5 N/m,τ=1.5 s。
通过和算例2相同的方法对非线性项和时滞项进行处理,利用暂态时积分求得包含阻尼时滞项的Van Der Pol方程的时域数值解。
分别采用MATLAB中时滞微分方程求解函数和本文方法对系统进行仿真,可得结果如图4所示。

时滞扰动项参数为:g=-1.51 N/m,τ=0.5 s

时滞扰动项参数为:g=-1.51 N/m,τ=0.5 s
仿真时间为600 s时,MATLAB dde23函数仿真数值结果共11 794个,步长间隔并不均匀。本文方法步长为0.000 1 s,相对于MATLAB方法计算步长更加精细。由图4可知,在仿真开始几秒钟,两种解法的结果存在小差异,原因与算例2相同,在几秒种后两种方法的结果几近一致。通过两种方法所解得的曲线,认为可取得相近的数值结果,并且本文方法更为精细,因此所得曲线更加光滑。
3 结论
(1)采用逐步递推的暂态时程积分方法对非线性微分方程进行求解,将非线性方程中的非线性项看作非齐次项。在每一段暂态时间区间内,方程中的齐次和非齐次项分别进行暂态时程积分计算,二者叠加可作为这一段时间历程内方程的实际状态。暂态时间逐步向前递推即可连续求得微分方程时域数值解。通过这种方法解得的非线性微分方程数值解和4阶Runge-Kutta法可以取得相近的数值结果,二者的误差在10-3左右。
(2) 对于包含时滞的非线性微分方程,将时滞项同样看作是非齐次项。在暂态时间区间内,通过分析时滞项的积分上下限确定时滞项的具体值,然后结合Romberg积分方法对时滞项进行积分计算。在Romberg积分过程中,对时间段内未知的时滞项值,通过线性插值的方法进行计算。通过这种逐步递推的暂态时程积分方法,求得的含时滞非线性微分方程的数值解和MATLAB函数的解大致相同,可以证明本文求解方法的有效性。并且本文方法相较于MATLAB解法更为精细,可控性更好,对方程中参数可以更方便地进行控制,为含时滞非线性微分方程的研究提供了新的路径。

