临河富水砂卵石层深基坑降水方案分析
何蕃民, 彭 涛, 邓 安, 李耀家, 杨华斌, 杨连枝
(1.中冶成都勘察研究总院有限公司, 成都 610023; 2.北京科技大学土木与资源工程学院, 北京 100083)
基坑降水是决定基坑工程成功与否的一个重要环节[1]。对于在临河砂卵石地层上的深基坑工程,因紧邻补给源、含水层渗透性强、基坑涌水量大等特点[2],基坑降水问题更加严峻。因此,如何控制好临河富水砂卵石层地层地下水是确保基坑安全施工的关键因素。
“大井法”[3]作为基坑降水方案设计中常采用的方法,也是中国实际工程中基坑设计规范采用的方法。该方法是将井群简化为一口大井,分别计算基坑总涌水量和单个降水井出水量,从而得出降水管井数量。中国基坑降水设计标准主要有《建筑基坑支护技术规程》(JGJ 120—2012)[4]和《管井技术规范》(GB 50296—2014)[5],其中《建筑基坑支护技术规程》未给出临河基坑降水方案的设计标准。《管井技术规范》对于临河基坑,考虑河流补给计算基坑总涌水量,确定降水管井布置的布置方案。
相关学者对基坑降水问题开展了大量的研究工作。薛丽影等[6]设计了基坑工程条件的模型试验系统,研究了完整井条件下的层状含水层渗流,获得与实际工程相符的渗流流网形态。Wang等[7]结合现场试验结果,基于Forchheimer方程,对基坑降水过程中的耦合非达西流动进行了数值模拟,研究了帷幕与抽水井不同组合方式下的耦合效应。刘历波等[8]采用MIDAS/GTS 岩土分析软件对邯郸市拟建建筑进行了渗流数值模拟,研究表明地下水由基坑外部向内部渗流,对基坑内部稳定性不利。徐永亮等[9]针对深厚卵石地层超深基坑降水问题,开展抽水、降水试验和数值模拟分析,指出对于形状不规则基坑,相比大井法,采用数值模拟定水位法计算开放式降水基坑涌水量更为合理。
对临河基坑降水问题,毛昶熙[10]采用“大井法”,给出了考虑河流不同补给方式下临河侧基坑涌水量的理论计算公式;刘俊龙[11]对位于潜水含水层中的近河基坑工程,讨论了《建筑基坑支护技术规程》中管井单井涌水量及基坑中某点水位降深计算公式的适用性及局限性, 并对相关计算公式进行了补充完善;Luo等[12]针对长江三角洲地区某深基坑降水工程,应用三维有限元数值计算方法,分析讨论了工程项目降水井布置方案,指出数值计算方法是该地区深基坑降水工程结构优化设计的基础理论;杨冬雪等[13]结合拉萨京藏交流中心邻河基坑降水项目的施工实践,分别比较了岸坡降水潜水非完整井和潜水完整井两种计算结果,并据此对邻河基坑管井降水的方案优化。可以看出,对于临河侧基坑降水问题,“大井法”和数值方法是基坑工程降水方案确定的常用方式。
现以具有复杂边界的某临河富水砂卵石层深基坑工程实例为背景,分别采用《建筑基坑支护技术规程》(JGJ 120—2012)、《管井技术规范》(GB 50296—2014)和临河基坑的理论公式进行降水设计分析,并辅助以精细化的数值方法,确定基坑降水设计方案,以期为调整基坑地下水提供科学依据。
1 工程概况
某临河基坑工程位于富水砂卵石地层上,东南侧有一条河流通过,河流转角为110°,河道宽度为15 m,距离基坑边10~20 m,河水位为498.18 m,基坑平面图如图1所示。基坑东西向长度为255.35 m,南北向长度为182.99 m,总面积为34 924.13 m2,开挖深度为8.0~11.00 m。项目场地绝对标高为502.45~503.95 m,基坑底部绝对标高为492.95~494.95 m。基坑施工过程中采用排桩支护方式进行支护,基坑降水采用管井降水。
依据项目勘察报告,场地地层主要由第四系全新统人工填土(Q4ml)、第四系全新统冲洪积层(Q4al+pl)及白垩系中统灌口组(K2g)泥岩组成。自上而下分别为杂填土①-1、粉质黏土②、粉土③、细砂④、中砂⑤、卵石层(松散⑥-1、稍密⑥-2、中密⑥-3、密实⑥-4)和泥岩层(强风化⑦-1、中等风化⑦-2),如图2所示。

图1 基坑平面图

图2 场地典型地质剖面图
本项目场地地貌单元系沱江水系Ⅰ级阶地,地下水类型主要为上部填土及粉质黏土层中的上层滞水、砂卵石中的孔隙型潜水及赋存于基岩中的基岩裂隙水,地下水位标高为498.60~499.66 m。砂卵石层为场地地下水的主要含水层,平均渗透系数值为20 m3/d。
2 基坑降水方案设计
工程实践中,基坑降水设计主要依据《建筑基坑支护技术规程》(JGJ 120—2012)和《管井技术规范》(GB 50296—2014)。第3.1和3.2节将分别采用这两个标准进行基坑降水设计。考虑到本项目东南侧存在河流补给边界,为基坑安全考虑,2.3节将采用毛昶熙[10]给出的临河基坑涌水量的理论解进行复核。
依据本项目勘察报告,项目场地标高取503.20 m,基坑标高取493.95 m,地下水位水位标高499.13 m。基岩埋深取最大埋深20 m,标高483.20 m。
2.1 《建筑基坑支护技术规程》推荐的方法
《建筑基坑支护技术规程》(JGJ 120—2012)未对靠河基坑的降水方案设计提供相应的指导,因而按照普通基坑进行设计。该工程的具体情况,采用均质含水层潜水完整井计算公式[4],对基坑降水进行设计。
(1)降水范围等效半径r0为

(1)
式(1)中:A为基坑面积,为34 924.13 m2。
(2)降水影响半径R为
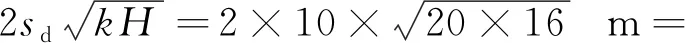
357.77 m
(2)
式(2)中:sd为基坑地下水设计降深,按基坑坑底最低标高492.95 m计算为6.68 m,取7 m。根据《规程》规定,当sd小于10 m,取10 m;H为含水层厚度15.93 m,取16 m。
(3)基坑降水总涌水量Q1(按均质含水层潜水完整井计算)为
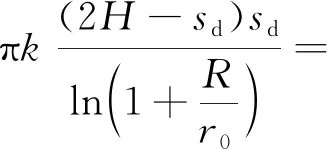
7 426.22 m3/d
(3)
式(3)中:k为渗透系数,依据项目勘察报告,取20 m/d。
(4)单井出水量q为
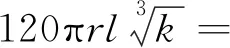
383.55 m3/d
(4)
式(4)中:r为过滤器半径,为0.15 m;l为过滤器进水部分有效长度,根据本项目支护及降水工程施工图设计报告,考虑到具体降水工艺及场地地质等情况,取2.5 m。
(5)管井数量n1为
(5)
按照《建筑基坑支护技术规程》计算,管井应布置22个,管井井距约为35.45 m。
2.2 《管井技术规范》推荐的方法
《管井技术规范》(GB 50296—2014)给出了靠河基坑的降水方案设计方法。采用均质含水层潜水完整井岸边降水计算公式[5],对基坑降水进行设计。
(1)基坑中心至河岸距离b为
b=15 m+105.46 m=120.46 m
(6)
(2)基坑总涌水量Q2为
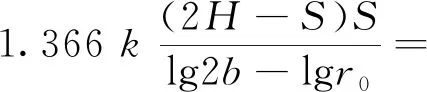
13 325.53 m3
(7)
式(7)中:降水范围等效半径r0同式(1)。
(3)管井数量n2为
(8)
式(8)中:q为式(3)得到的单井的涌水量。按照《管井技术规范》计算,管井应布置39个,管井井距约为20.10 m。
2.3 临河基坑涌水量理论公式
毛昶熙[10]给出了考虑不同河流补给条件下基坑的降水影响半径的理论公式。结合本项目实际,由图1可知,基坑东南角会同时受到东侧和南侧的河流补给边界的影响(河流转角110°)。为得到更符合本工程项目的涌水量计算,考虑图3所示的两种补给边界,采用影响半径的理论公式分别计算其涌水量和管井数。
2.3.1 单侧补水条件
计算图3(a)单侧直线水源补给条件下的基坑涌水量和管井数目。图3(a)中的L为基坑中心至河岸线的距离,计算为120.46 m。
(1)影响半径R1为
R1=2L=2×120.46 m=240.92 m
(9)
(2)基坑涌水量Q3为
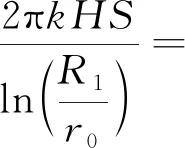
17 027.77 m3/d
(10)
(3)管井数量n3为
(11)
因而,对于单侧直线河流补给的情况,理论解算出基坑应布置49个管井,管井井距约为15.92 m。
3.2.2 直角两侧补水
设L1=L=120.46 m,按图3(b)所示计算基坑影响半径,再计算涌水量和管井数。
(1)影响半径R2为
(12)
(2)基坑涌水量Q4为

29 332.20 m3/d
(13)
(3)管井数量n4为
(14)
按85个管井布置,管井井距约为9.17 m。

图3 基坑在不同边界条件下的影响半径
因而,对于直角两侧河流补给的情况,理论解算出基坑应布置85个管井,管井井距约为9.17 m。
2.4 讨论
将上述计算的基坑涌水量、管井数量、井距结果汇总,如表1所示。从计算的基坑降水总涌水量来看,由于《建筑基坑支护技术规程》给出的基坑涌水量计算公式未考虑河道对基坑地下水的补给,计算得出基坑涌水量最小,为7 426.22 m3/d,井距35.45 m;《管井技术规范》岸边降水公式计算结果为13 325.53 m3/d,井距为20.10 m;单侧河流补给临河基坑涌水量理论解计算为17 027.77 m3/d,井距为15.92 m;直角两侧补给的理论解得到的基坑涌水量为29 332.20 m3/d,井距为9.17 m。可见,考虑补水边界计算的基坑涌水量比前两个标准的计算结果要大,而采用直角补给边界计算的涌水量更是基坑标准计算结果的4倍。由此可得,对于临河基坑降水计算应高度重视,为确保基坑安全,有必要采用多种计算公式相互复核校正。
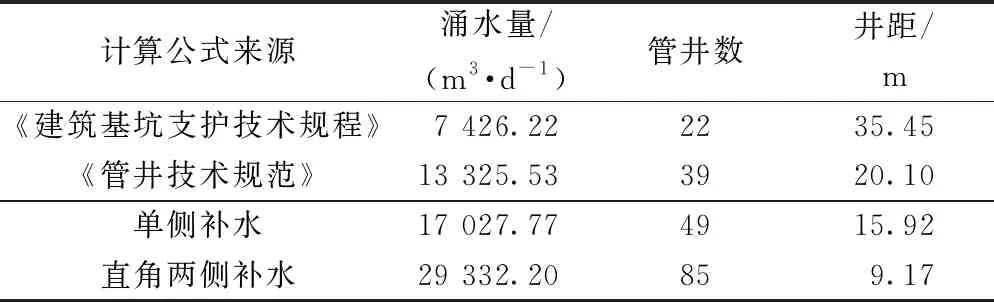
表1 基坑涌水计算结果
在本项目基坑降水设计中,依据国标《管井技术规范》计算结果进行基坑降水井布置,沿基坑周围共设置39个降水井,具体布置如图1所示。管井井深度20 m,直径350 mm。水泵功率7.5 kW,最大扬程30 m,最大排水量35 m3/h。然而,当开挖接近基坑底时,基坑临河侧G-H-I-J段出现不同程度积水,积水面积约7 000 m2(图1阴影区域),其中积水最深约1 m。
由此可见,本项目按照国标《管井技术规范》布置的管井数显然是不够的,有必要考虑直线和直角河流补给的理论解。鉴于基坑东南角河流的转角大于90°,因而基坑的涌水量和管井数可在单侧直线和两侧直角补给两种之间取值。下面将借助数值分析手段对基坑降水进行辅助设计。
3 基坑降水方案的数值辅助设计
3.1 计算方法
饱和-非饱和渗流的偏微分方程表达式为[14]
(15)
式(15)中:θ为土体的体积含水率;kr为相对渗透系数(0≤kr≤1);Kij为介质饱和渗透张量;h=ψ+z为水头;ψ为压力水头(ψ>0土体饱和,ψ≤0土体非饱和);z为参考平面上的高程;Q代表源项;i,j=1,2,…,D指几何坐标下标,D为空间维数;t为时间。
非饱和土体的含水率与毛细水压(吸力水头)的关系可通过Maluem公式[15]表示,即
(16)
式(16)中:θs为饱和体积含水率;θr为残余体积含水率;α为和平均粒径大小有关的参数;n为和粒径均匀性有关的参数;m=1-1/n。
土体非饱和相对渗透系数kr与饱和度的关系常采用Van Genuchten公式[16],即
(17)
式(17)中:se为有效饱和度,与含水率关系公式为
(18)
根据毛细水压,通过式(16)、式(17)和式(18)即可得到土体的非饱和计算参数:饱和度和相对渗透系数。通过式(15)进行空间和时间离散,可建立起土体饱和-非饱和渗流有限元数值计算方程,具体推导过程详见文献[14]。
3.2 计算模型及参数
以靠近河道基坑G-H-I-J段(图1)作为研究对象。考虑到管井沿基坑四周均匀布置,假定地下水流动主要发生在垂直于河道的平面内,取图1中26号井两侧半个井距作为数值模型计算区域(图4)。模型范围:右侧取河道中心线;左侧取一倍基坑深度,即基坑内侧10 m处;顶面为场坪标高502.45 m;底部范围取至基岩面以下10 m(高程478 m)。为研究不同井距的降水性能,取管井间距L为20、10、5 m 3组工况进行计算。
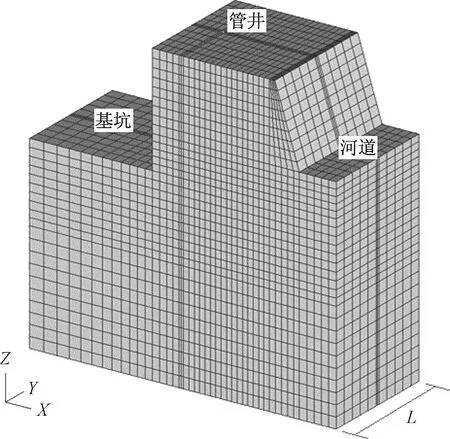
图4 三维计算模型(L=20 m)
根据现场钻孔资料,并为简化计算,对渗流系数比较接近土层合并,具体为杂填土、素填土、粉质黏土、粉土简化为粉土层,细砂、中砂、卵石层简化为砂卵石层,泥岩层分为强风化泥岩和中等风化泥岩层,如图5所示。管井边壁取为溢出面边界(井水内水位取设计水位486.23 m),基坑坑底面和基坑内壁截面取为可能的溢出面边界(溢出面水位设为基坑坑底高程493.45 m),溢出面边界具体设置如图5中蓝粗线所示,其余为不透水边界。
本项目勘察报告仅给出砂卵石含水层经验渗透系数建议值,取20 m/d;其他土层计算参数参考同地区类似工程[17],各土层饱和渗透参数如表 2所示。饱和-非饱和计算参数采用给定饱和度、毛细水压、相对渗透系数的关系曲线,饱和度与毛细水压的关系曲线如图6所示,饱和度与相对渗透系数的关系曲线如图7所示。

图5 计算模型地层剖面及边界

表2 土体计算系数
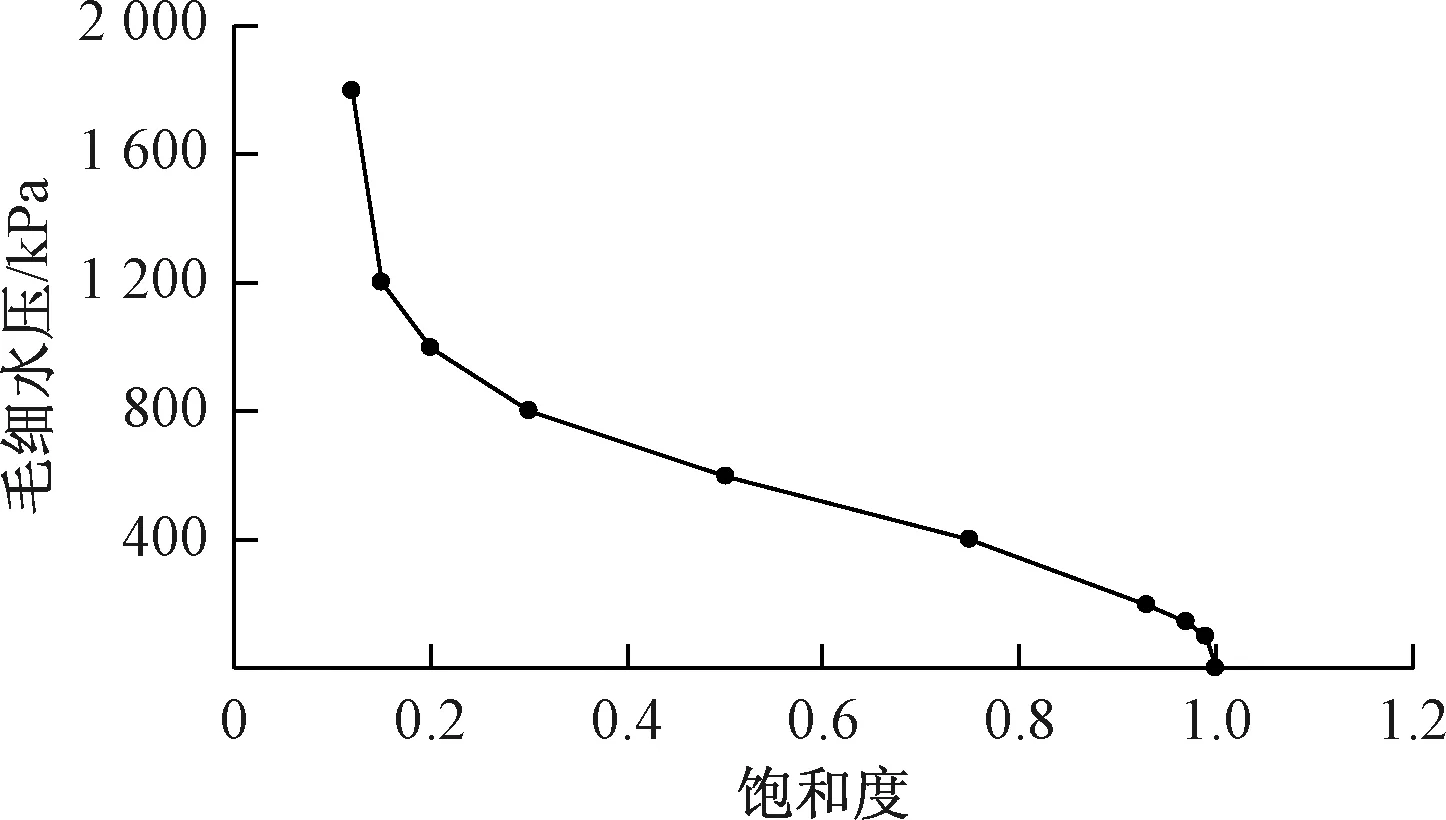
图6 饱和度与毛细水压的关系曲线
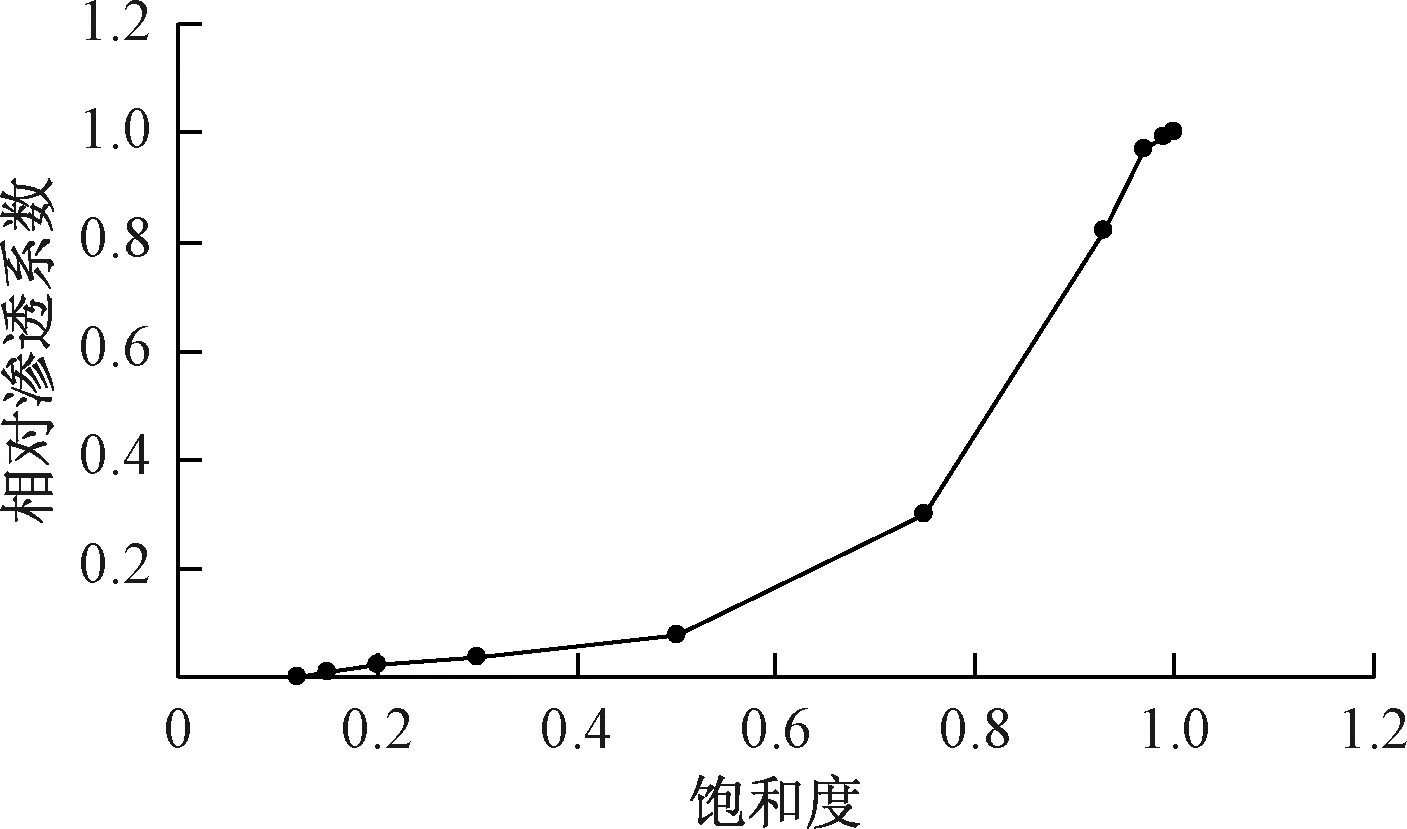
图7 饱和度与相对渗透系数的关系曲线
3.3 基坑地下水渗流分析
以管井间距10 m为例,分析基坑地下水渗流特性。基坑底部水平断面水头等值线分布如图8所示。水头等值线自右侧(河道)向左侧(基坑)逐渐降低,水头降低约为3.8 m。由此可以看出,河道水流是影响基坑东南区域地下水的首要因素。
为更加清晰呈现基坑降水管井附近地下水渗流特性,分别考察图8中Y=5 m剖面(管井剖面)和Y=0剖面(相邻管井中心剖面)饱和区的水头等值线,如图9、图10所示。从管井剖面水头等值线可以看出,受基坑施工降水影响,水头等值线在靠近从河道至管井呈现不断下降趋势,水头最大降低为8.68 m,约靠近管井,等值线越密集,水头下降越快。但相邻管井中心剖面水头等值线分布较为均匀(图10)。可见,管井降水对相邻管井中心剖面水头等值线分布的影响已明显减弱。

图9 基坑Y=5.0 m剖面(管井剖面)水头等值线
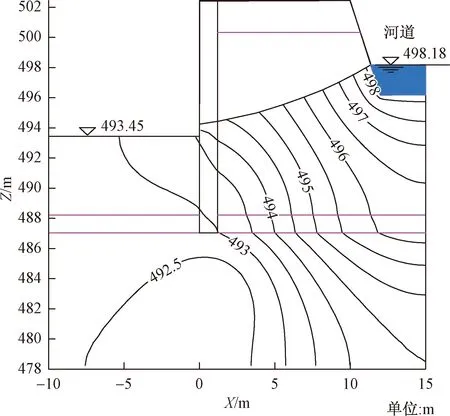
图10 基坑Y=0 m剖面(相邻管井中心剖面)水头等值线
3.4 不同井距降水效果分析
降水管井间距分别为20、10、5 m时,管井剖面孔隙水压力等值线如图11~图13所示。可以看出,水压力等值线在管井处仍较为密集,呈现出降水“漏斗”形状。按照采用《管井技术规范》设计降水方案(管井间距为20 m时),数值模拟计算出基坑底部孔隙水压力约为9 kPa,也即意味着基坑底部将会出现约0.9 m的积水,与施工中遭遇的情况基本吻合。
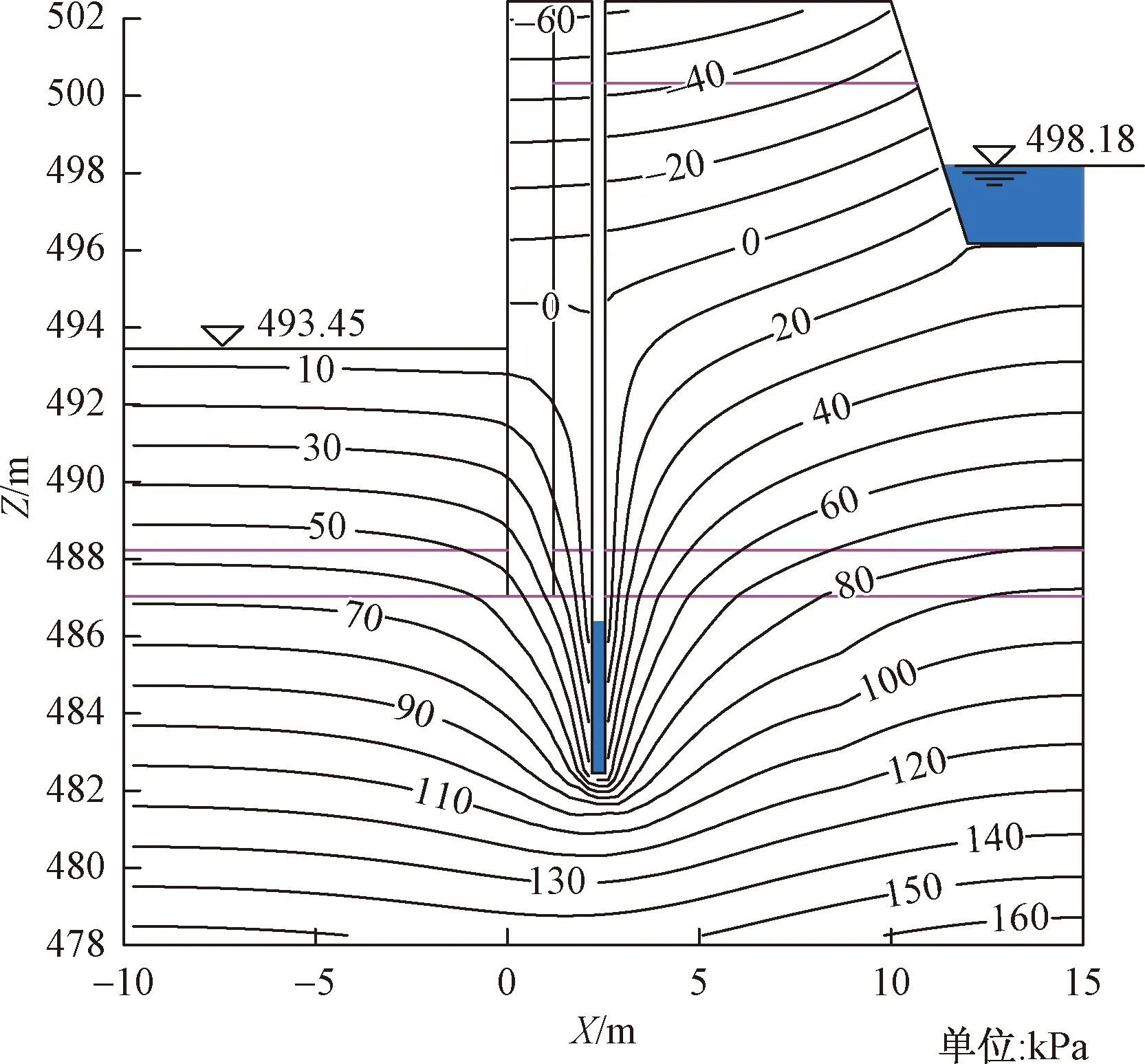
图11 井距20 m的管井剖面孔隙水压力等值线(设计方案)
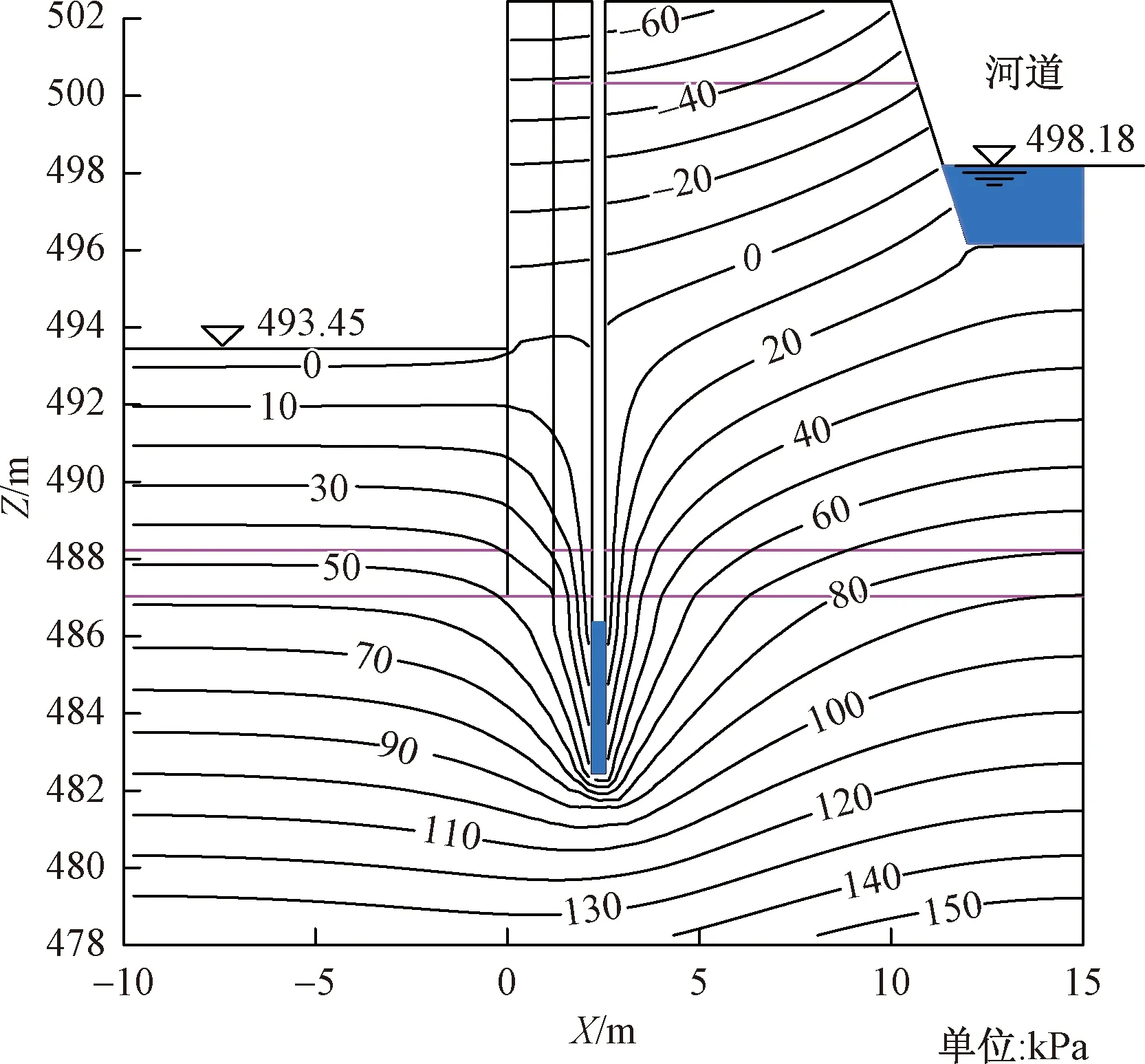
图12 井距10 m的管井剖面孔隙水压力等值线
当管井间距减少至10 m时,孔隙水压力零压力线下移至基坑底部约0.4 m(图13),基本满足基坑降水施工要求;当管井间距进一步降至5 m时,零压力线进一步降低,至基坑底部以下约1.5 m。
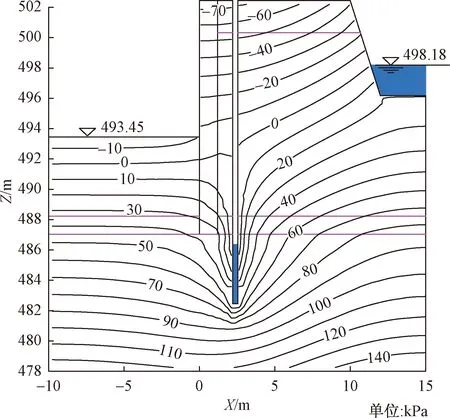
图13 井距5 m的管井剖面孔隙水压力等值线
通过数值模拟分析,对于靠近河道一侧的管井间距按20 m,将无法满足施工要求,合理的管井间距应控制在5~10 m。
4 基坑降水方案确定
由前文计算分析可知,按照《管井技术规范》设计的管井间距20 m并不能满足该基坑东南侧的降水需求。实际在施工过程中,基坑底部东南角也确实出现了积水现象(图1)。采用毛昶熙[10]提出的河流补给的理论解来确定井距,则基坑降水井的井距选择在9.17~15.92 m。对基坑东南侧河流拐弯处的降水管井的控制区域渗流场计算分析可知,管井距在5~10 m是比较合适的。结合理论解和数值解,最终确定基坑东南侧的管井井距在9~10 m。
根据计算成果,采用对基坑东南区域降水管井局部进行局部加密,以加大基坑降水力度。沿基坑河流侧新增13个降水管井,如图14所示,结合到场地条件,其中4个管井布置在坑内,7个管井布置在坑外。加密后,基坑河流侧管井井距最大值为11.5 m,最小值为7.3 m,平均间距9.33 m。新增13个降水管井投入运行后,有效降低了基坑地下水位。经施工现场勘查,基坑内部地下水水位控制在基坑底部1 m以下,满足施工要求。

图14 新增降水井位置
5 结论
针对某临河富水砂卵石层深基坑工程实例,分别采用《建筑基坑支护技术规程》《管井技术规范》和毛昶熙[10]给出的临河基坑的理论公式进行降水设计分析,并辅助以精细化的数值方法进行验证分析,得出以下结论。
(1)本工程案例中,《建筑基坑支护技术规程》计算出的管井间距最大,为35.45 m;设计方案采用的《管井技术规范》得出的管井间距次之,为20.10 m;临河基坑的理论公式计算得出的管井间距最小,分别为15.92 m(单侧补水)和9.17 m(直角两侧补水)。
(2)对临河侧管井间距为20 m(设计方案)、10 m和5 m 3种工况进行了数值模拟,计算得出管井间距为20 m时,基坑底部存在0.9 m积水,与实际施工情况基本吻合。结合理论公式计算和数值模拟结果,确定基坑东南侧的管井井距在9~10 m,并据此结果,沿基坑临河侧新增了13个降水管井,解决了本项目基坑降水问题。
(3)由本案例可知,对于临河的基坑降水设计时,应充分考虑河流补给的影响。利用规范、结合理论和数值手段的分析方法,是对复杂边界条件下深基坑降水方案设计比较好的方式,具有广阔的应用前景。

