基于行波衰减理论的多端直流网络故障定位
张怿宁, 方 苏, 罗国敏, 刘燕莹, 黑嘉欣
(1.中国南方电网超高压公司检修试验中心, 广州 510663; 2.北京交通大学电气工程学院, 北京 100044)
随着中国新能源发电快速发展,同时受发电能源与用电负荷逆向分布的制约,中国存在大规模电能输送的需求。由于电力电子器件的成本低、可靠性高,柔性直流输电技术是一种控制灵活方便、高效的新型高压直流输电技术[1],使得电网互联更方便,在诸多方面应用前景广泛,逐渐形成了多端直流输电系统[2]。多端直流输电常采用架空线,架空线经过不同的气候和地形环境,是柔直输电系统中故障率最高的元件[3-4]。线路故障后,及时、正确地找到故障点,不仅提高了电力系统的可靠性,而且可以减少停电造成的经济损失,因此有必要研究多端柔直输电线路故障定位[5-6]。
直流断路器的是多端直流系统发展和应用的瓶颈,近几年混合式直流断路器的出现,增强了多端直流电网的稳定性。但是直流断路器的造价十分昂贵,制作工艺复杂,研发难度大,技术要求高。浙江舟山五端工程中只有舟定一端配置了直流断路器[7],线路发生故障后,影响区域也增大。针对以上情况,为了保证在无直流断路器的多端系统发生故障后,仍然可以快速准确找到故障点进行了一些研究。
无直流断路器的多端直流输电系统的故障定位包括判断故障线路和计算故障位置。一方面,由于直流系统的故障特征与交流系统的差异,传统交流电网中基于序分量的各种故障定位法[8]已不适用;另一方面,多端直流输电网拓扑千变万化,传统点对点直流系统中常用的各类故障定位方法,如故障分析法[9-10]、固有频率法[11-13]和行波法[14-15],只能用来计算故障线路上的故障距离,而不能识别故障线路,因此不能直接应用到多端直流系统中,多端直流输电系统的故障定位面临着许多挑战。中外学者对多端系统进行许多研究,针对树状网络,文献[16]提出利用零模和线模行波分量速度差的故障测距算法,由于只判断行波的初始波头到达时刻,所以不受分支的影响。针对星型连接的三端系统,文献[17]给出了计算波速和定位方法,该方法在已知故障位置的基础上先求波速,然后在实际故障中利用波头时刻和波速进行故障定位,并且此方法可推广到N端星型网络。针对多端网状环型结构,文献[18]提出了基于扰动初始行波波头到达时刻的广域行波定位方法。文献[19]利用换流站检测的初始行波波头时刻及线路长度排除一些非故障线路,根据评估指数识别故障线路,最后故障测距。文献[20]提出了在部分换流站安装行波记录仪的广域系统中的故障定位方法,利用初始行波时刻得到曼哈顿距离矩阵,找到正确的测量组合,得到初步定位结果,最后通过时间及拓扑关系验证结果的正确性。针对不满足三角形原则的多端系统,文献[21]提出了基于最小故障发生时刻的故障定位方法。以上各种拓扑多端系统的故障定位方法,都是基于识别初始行波波头进行故障定位。在文献[21]的仿真模型基础上,现提出另一种故障定位方法,针对无直流断路器的多端直流系统,首先,对多端系统的拓扑和限流电抗器影响及多端定位总结,然后结合多端系统的拓扑结构,分析不满足三角形原则的多端系统的盲区问题,基于行波衰减理论提出方法,阐述具体步骤。最后在四端模型中进行仿真验证。
1 多端直流系统定位问题分析
1.1 多端直流系统拓扑
直流输电系统拓扑分为双端和多端结构,多端直流拓扑如图1所示,有树状、星型、环型,由于线路长度不同,环型结构分为满足三角形原则结构和不满足三角形原则结构。
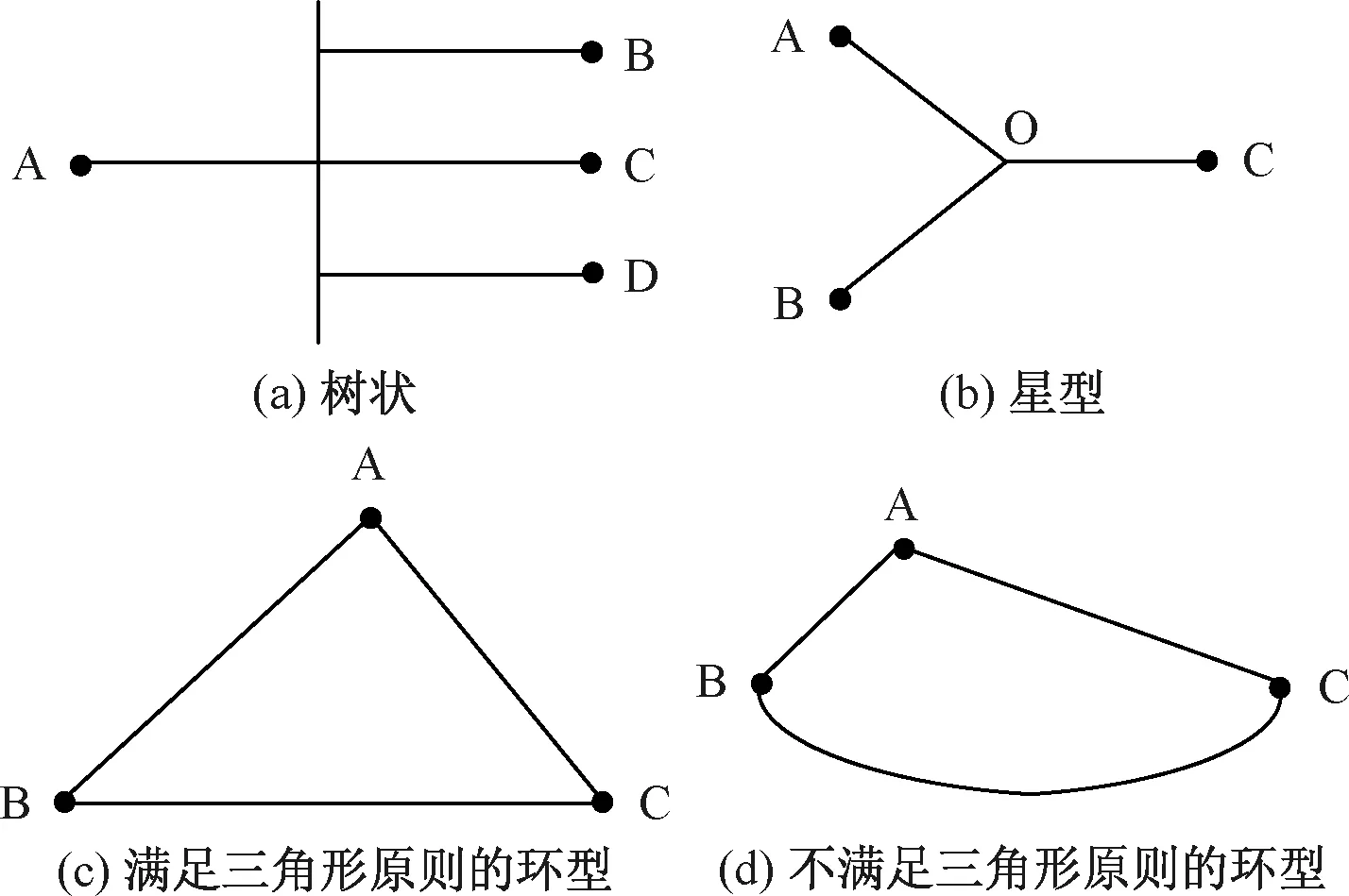
图1 多端直流系统的拓扑类型
对树状和星型开环结构,故障发生后,故障行波从故障点到测量点的传播路径只有一条。而对环型结构,由于是闭环网络,故障行波到每个测量点存在多条路径,其中一条线路故障后,只利用初始行波故障信息,定位准确度不高。对不满足三角形原则的环型结构,可能故障线路定位错误,因此有必要考虑新的故障定位算法。
1.2 限流电抗器的影响
由于少数多端直流工程在线路两端安装限流电抗器以减小故障对电网的影响,所以本节分析了限流电抗器大小对行波的影响如图2所示。
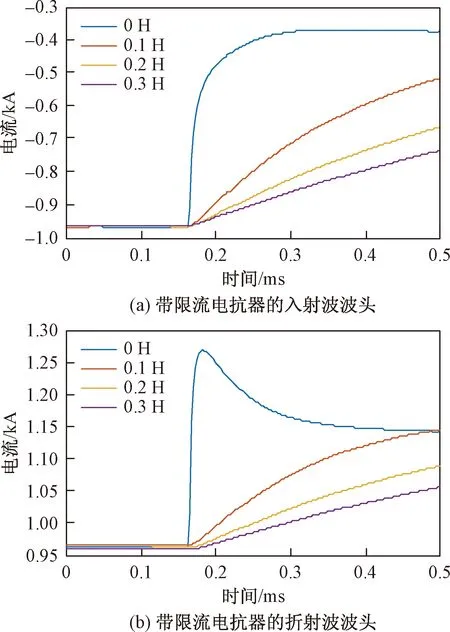
图2 限流电抗器的影响
由图2可知,增大电抗器的值会降低行波幅值,延缓电流上升速度,使得行波波头变缓。对于装设限流电抗器的多端系统,区内故障时波头变化幅度较大,区外故障时波头检测困难,区内外故障特征明显,可有效辨识故障线路。然而,这样的工程较少,所以针对无限流电抗器这样的多数多端直流系统进行研究。
1.3 多端定位
由于拓扑结构的不同,多端直流输电线路故障定位存在很大差异。对树状、星型以及满足三角形原则的环型结构,故障点到测量点的直接路径即为最短路径,可使用初始行波定位。
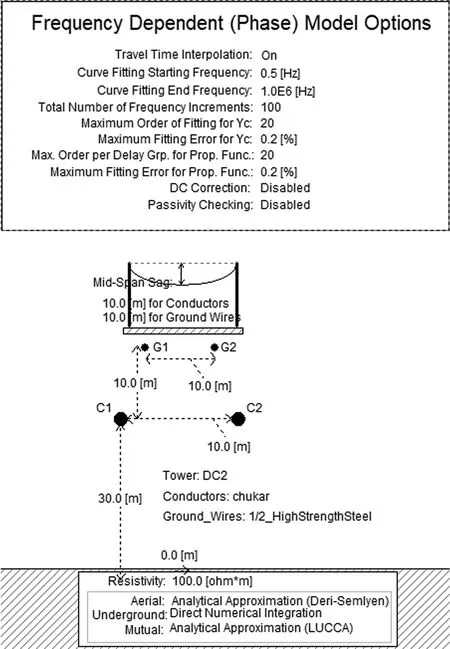
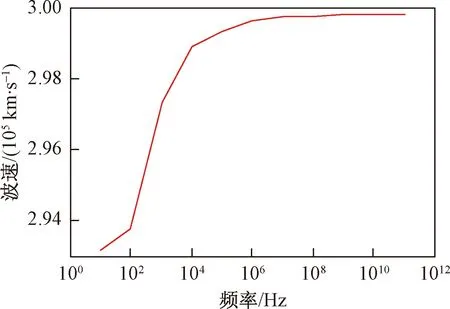
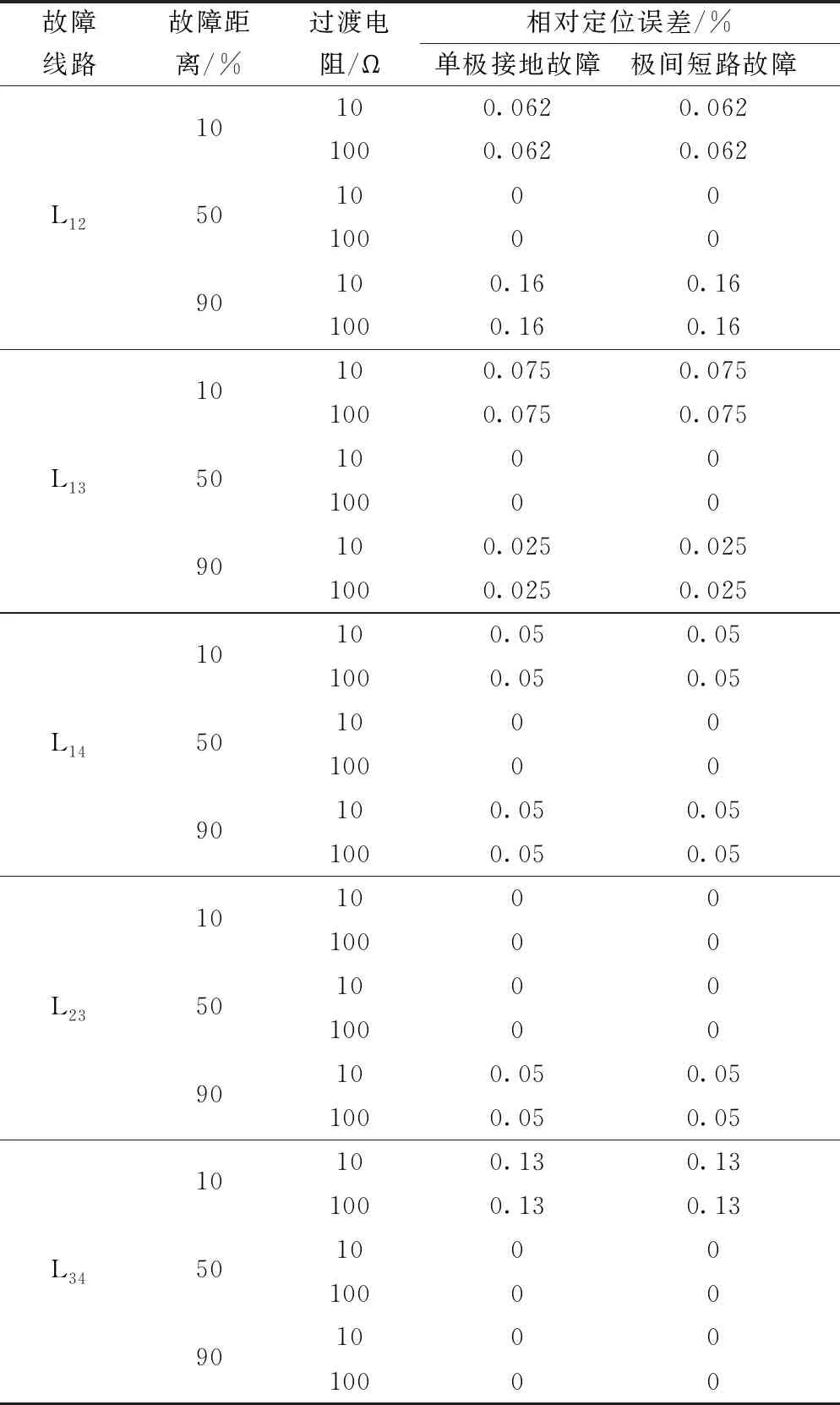
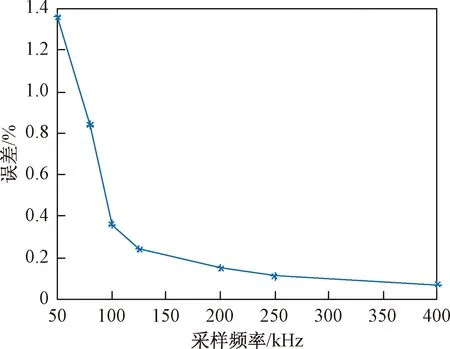
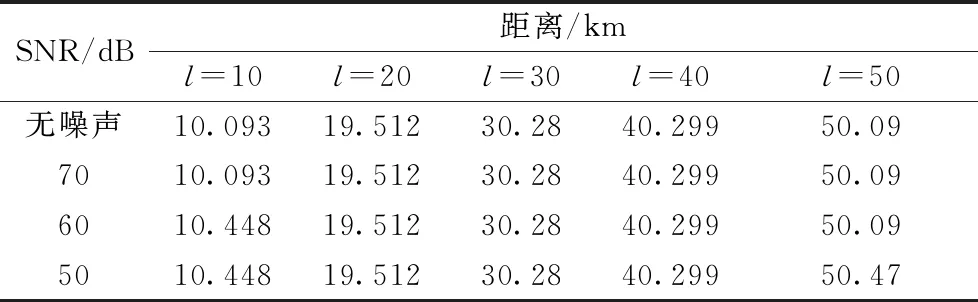
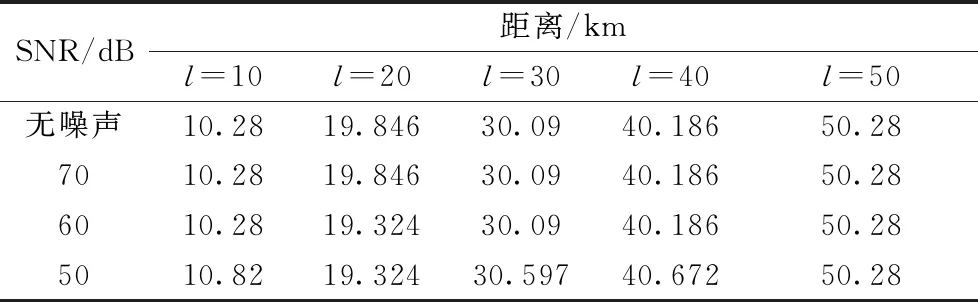
在不满足三角形原则的多端环型结构中,如图3所示,利用初始行波进行故障定位存在盲区问题。行波记录仪安装在A、B、C 3个换流站,换流站之间的距离分别为lAB、lAC、lBC,lAB+lAC 图3 三端直流输电系统模型 利用初始行波定位,将通过行波最短路径得到的计算结果作为故障距离,测距精度会受影响,甚至会出现错误的定位结果。出现错误结果的故障点f的位置区域称为盲区,位于最长线路LBC两端附近,如图3中的BB′和CC′,且两端盲区相等,用式(1)表示为 (1) 式(1)中:lblind为盲区的长度,km;lAB、lAC、lBC分别为线路LAB、LAC、LBC的长度,km。 由式(1)可知,盲区大小取决于最长线路长度lBC和其余线路长度之和lAB+lAC的差。差值越大,盲区越大。为解决多端环型结构中的盲区问题,对行波的传播特性展开研究。 线路故障后,可等效为在故障点加一个电压源,该电压源产生电压波和电流波。电流波又分为入射波、折射波和反射波。行波传播特性是故障定位的基础,故对多端系统行波的传播特性展开研究。 多端直流系统线路故障后,电压波和电流波沿故障线路传播到两端换流站。线路传播距离与入射电流波在线路上衰减情况如图4所示。 由图4可知, 行波传播的距离越长,衰减程度越严重,且行波在电缆中传播的衰减程度大于架空线路。电流入射波在沿架空线路和电缆传播500 km后幅值分别衰减为原来的0.8、0.5。 图4 入射波在线路上的衰减 线路均匀性遭到破坏的点称为节点,多端柔性直流系统中,线路的均匀性在经过分支时遭到破坏。当行波传播到节点时,在节点处发生折反射。由于所用线路均为参数相同的架空线路,即各线路波阻抗相等,因此可忽略行波在节点处的反射,只考虑折射情况。 多端环型结构中,假设一条母线上有N条线路,其中一条线路故障,根据彼德逊法则,故障线路上入射电压波U0或者电流波I0传输到母线节点T时,连接到母线节点的其他线路上的折射电压波和电流波分别为 (2) 式(2)中:UT为经母线分支折射的电压波,kV;IT为经母线分支折射的电流波,kA;U0为故障线路上产生的电压波,kV;I0为故障线路上产生的电流波, kA;N为母线公共节点上所连的分支数。 根据式(2)不难得出,当母线公共节点上所连的分支数N越多,折射电压波和电流波衰减越严重。实际应用中,环型结构的公共节点最少连接两条输电线路,N最少为2,行波幅值折射衰减至少为原来的1/2。所以,行波经分支折射衰减比其在线路上的衰减程度大得多。 图3中的f点发生故障,行波传播路径f-B′-C′-C和f-B-A-C分别记为直接路径(direct path,DP)和间接路径(indirect path,IP)。两条路径在C点检测到的故障行波波头如图5所示。 由图5可知,DP衰减程度小于IP,即行波在线路上的衰减程度小于经过公共节点发生折射的衰减程度。 图5 两个行波波头的对比 无直流断路器的多端直流输电系统中,查找故障线路和计算故障距离是故障定位的主要任务。同时确定波速和标定波头时刻是计算故障距离的关键,而波速难以直接确定且随频率变化。所以提出一种新的研究思路:首先根据波速的频率特性确定参考波速范围,再测定实际波速,通过对比波速大小排除部分非故障线路以及确定实际波速。此外希尔伯特-黄变换可用于标定幅值变化最大的波头时刻。根据波速和最大行波波头时刻实现多端系统的故障定位。基于行波衰减理论的故障定位算法流程如图6所示。 图6 基于行波衰减理论的故障定位算法流程 实际输电线路,单位长度的电感和电容是随频率变化的,而波速又与线路参数相关,所以频率改变时,波速随之改变[22],即 (3) 式(3)中:v为波速,km/s;w为角频率,rad/s;Z为线路的阻抗,Ω/km;Y为线路的导纳,S/km;Im表示取虚部计算。 仿真系统模型的架空线路的频率相关模型如图7所示,架空导线距地面高度为30 m,接地线与导线上方的垂直距离为10 m,双极导线水平间距为10 m,由线路模型可得波速的频率特性如图8所示。由于零模波速不稳定,对测距精度影响也较大,线模波速相对较稳定,因此以线模波速作为参考波速。由于线模波速的低频较符合正态分布且不超过光速,根据正态分布的3σ原则得到波速的最小置信区间为2.957 8×105~3×105km/s。 C1和C2分别代表直流正负极线路;G1和G2分别表示两条架空地线(也就是两条避雷线) 图8 线模波速的频率特性 对暂态线模电压进行经验模态分解(empirical mode decomposition,EMD),得到信号不同频率的固有模态函数(intrinsic modal function,IMF),对第一个固有模态函数求一阶差分,利用一阶差分最小值点准确标定行波幅值变化最大的波头时刻,时间窗宽度是行波经过最长线路所用时间。 区外故障时,行波将穿越整条线路,利用换流站间的距离和波头到达时间差测定在线波速为 (4) 式(4)中:vij为在线测量的波速,km/s;lij为线路Lij的长度,km;ti和tj分别为线路Lij两端检测到的幅值变化最大的行波波头时刻,s。 在线测量波速个数等于多端系统中线路数量。若测得的行波波速vij接近光速且在参考波速区间内,则故障发生在区外,即线路 Lij是非故障线路。多端系统线路数多,符合条件的波速不止一个,为了减小测量误差,取满足条件的波速平均值作为故障定位波速v。 由3.3节将部分非故障线路排除,依次假设其他线路故障,利用式(5)计算相应的故障发生时刻。故障发生时刻个数等于其他假设故障线路个数。 (5) 为找到故障线路,计算其他假设故障线路到达各个换流站的时间矢量。通过假设故障线路两端记录的最大行波波头时刻和线路长度及波速,计算行波到达时间矢量。到达时刻矢量Tai的个数等于假设故障线路的数目。 将计算的到达时间矢量Tai与行波记录仪记录的到达时间矢量Tm之间的欧式距离进行比较。若假设故障线路是实际的故障线路,则计算得到Tai和行波记录仪记录的Tm相等,否则,是不同的。如上所述,利用欧式距离的最小值可识别出实际的故障线路,如式(6)所示。若假设故障线路有n条,则得到n个欧式距离。 Dmin=min(D1,D2,…Di)= i=1,2,…,n (6) 式(6)中:Dmin为最小欧式距离,s;Di为第i个假设故障时间矢量之间的欧式距离,s;Tai为第i个假设故障计算的到达时间矢量,s;Tm是行波记录仪记录的到达时间矢量,s。 根据3.5节可识别故障线路,若故障线路Lij的长度为lij,将线路两端最大的波头时刻以及波速代入式(7)中,得到故障距离。 (7) 式(7)中:lcal为故障距离,km。 为验证所提方法的准确性, 在 PSCAD上搭建一个± 200 kV四端柔性直流输电线路模型,如图9所示。换流站1采用定直流电压和定无功功率控制模式,换流站2、3、4均采用定有功和定无功功率控制策略。线路单位长度参数R=0.034 46 Ω/km,L=1.287 mH/km,C=9.030 7×10-3μF/km。系统采样频率为400 kHz,4个换流站母线节点处均设置同步测量装置。 图9 四端柔性直流输电线路模型 以图9所示的故障位置为例,对定位方法的进行测试。故障发生位置距换流站4为10 km,故障类型为单极接地,过渡电阻为0.01 Ω。根据1.3节分析可知,该故障发生在盲区。换流站3母线处,检测的初始行波和幅值变化最大的行波分别是间接路径f-4-1-3和直接路径f-3传播过来的。系统的最长线路L34为600 km,数据窗宽度为600 km/(30 000 km/s)=0.002 s。换流站3的线模电压和线模电压的第一个固有模态函数IMF1的一阶差分如图10、图11所示。 由图10、图11可知,初始行波幅值变化较小,第二个行波幅值变化最大,一阶差分的最小值点对应幅值变化最大的行波波头到达时刻,记为t3。 图10 换流站3的线模电压 图11 IMF1分量的一阶差分 当故障发生时刻为t0=0 s时,4个换流站的行波幅值变化最大的波头到达时刻如表1所示。 表1 各个换流站的最大行波波头到达时刻 根据行波幅值变化最大的波头到达时刻以及换流站间的距离,利用式(4),得到在线波速v12=2.996 3×105km/s,v13=2.496 1×105km/s,v14=2.985 1×105km/s,v23=3.208 6×105km/s,v34=3.096 8×105km/s。线路L12、L14上的波速接近光速且在参考波速区间内,所以线路L12、L14是非故障线路,取v12和v14的平均值作为故障定位所用波速v。 其余假设故障的计算值如表2所示,L13、L23,L34分别是从站1、 2、 3出发计算的。根据行波幅值变化最大的波头到达时刻,利用式(5)计算出相应的故障发生时刻、故障距离和到达时间矢量,最后将表1记录的时间矢量和表2中计算的时间矢量代入式(6)得到各个欧式距离。 由表2可知,线路L34的欧式距离最小,所以判断L34是故障线路,距离换流站3为589.720 6 km,距离换流站4为10.279 4 km,绝对误差为0.279 4 km,满足相关要求,即对于超过300 km的长线路,测距误差最大不超过1 km,定位精度较高。 为了验证本文方法的准确性,在不同故障条件下仿真,相应定位结果和误差如表3所示。误差是相对定位误差,为|lcal-lact|/lline,lcal是仿真计算的故障距离,lact是实际故障距离,lline是故障线路长度。相对误差越小,表明定位精度越高。当误差低于1.397 5×10-6时,近似认为误差为0。 由表3可知,基于行波衰减理论的多端直流网络故障定位法,最大相对定位误差是0.13%,误差较小,测距精度较高。当故障发生在线路中点,从故障点到线路两端的距离相等,所以两端点的行波波头时间差较准确,定位误差较小。 4.3.1 故障距离的影响 分别在线路L13、L34上距换流站1、换流站3为10~300 km设置单极接地故障,故障电阻为0.01 Ω,步长为10 km,相对定位误差随故障距离变化如图12所示。 由图12可知,相对误差在0~0.15%,表明本文所提方法定位误差较小,准确性较高。 表2 假设故障的计算值 表3 不同故障条件下的定位结果 图12 不同故障距离的定位误差 4.3.2 采样频率的影响 行波波头标定的精度与采样频率有很大关系,采样频率对定位的影响如图13所示。线路L13上距换流站1为30 km处发生单极接地故障,过渡电阻为0.01 Ω。 由图13可知,采样频率越高,定位误差越小。 图13 不同采样频率的定位误差 4.3.3 过渡电阻的影响 基于行波的故障定位法优点之一是对过渡电阻的鲁棒性。采用0~100 Ω一组过渡电阻仿真,步长为20 Ω。分别在线路L13和L34上距换流站1、换流站3为30 km处发生单极接地故障,相对定位误差E13、E34随过渡电阻的变化如表4所示。 由表4可知,在一定范围内,过渡电阻的变化并不影响本文方法定位的精确度。 表4 不同接地电阻的定位误差 4.3.4 噪声的影响 实际系统中,测量到的行波混杂有不同成分的噪声,如高斯白噪声,有可能会对故障定位的结果产生影响。在线路L13、L34上距离换流站1、换流站4为10、20、30、40、50 km处发生单极接地故障,过渡电阻为0.01 Ω。将不同幅度的高斯白噪声添加到仿真系统得到的电压波信号中,故障距离随信噪比(signal to noise ratio,SNR)的变化如表5、表6所示。表5中l代表线路L13上故障点距离换流站1的距离,km。表6中,l代表线路L34上故障点距离换流站4的距离,km。 表5 不同噪声下线路L13的定位结果 表6 不同噪声下线路L34的定位结果 由表5、表6可知,在一定范围内,噪声不会对定位方法产生大的干扰,具有一定的抗噪声能力,而且噪声越小,定位越准确。如果噪声太大,就需要加去噪设备。 无直流断路器且不满足三角形原则的环型多端直流系统存在盲区问题,为了解决此问题,提出了基于行波衰减理论的故障定位方法,通过仿真,可得如下结论。 (1)利用希尔伯特-黄变换确定行波幅值变化最大的波头时刻,在线测量波速度,本文方法很好地解决盲区问题。 (2)不同故障情况的定位结果表明,无论是单极接地故障还是极间故障,本文方法测距精度都较高,受故障距离、过渡电阻、噪声的影响较小,有效地提高了多端直流输电系统故障定位的准确性。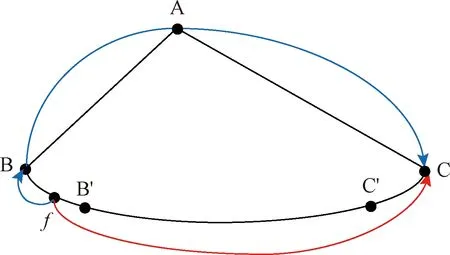
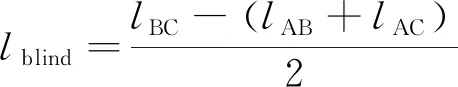
2 多端系统行波传播特性
2.1 行波在线路上的衰减
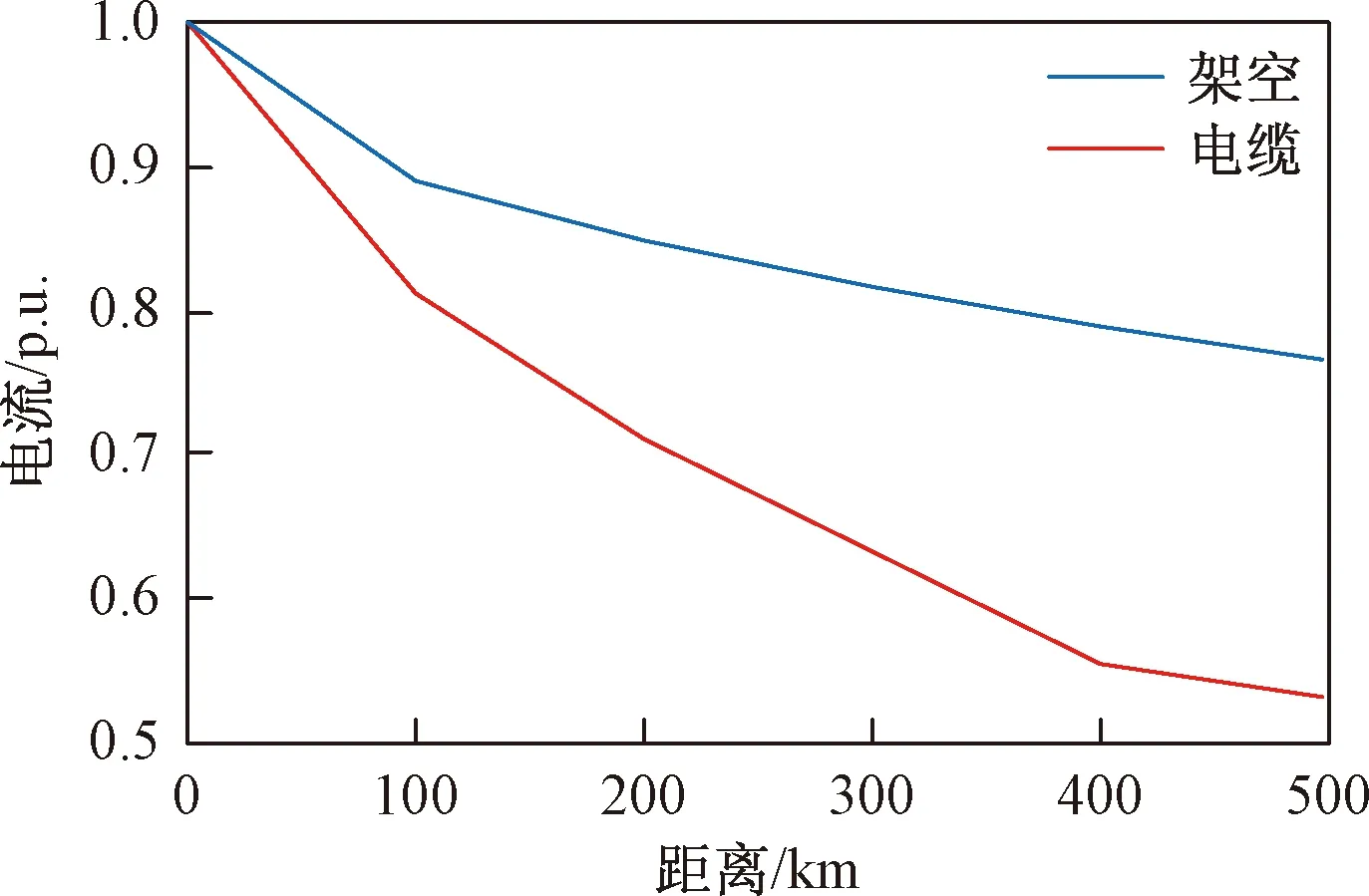
2.2 行波经过分支的衰减
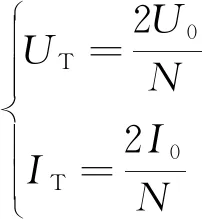
2.3 行波衰减特性对比
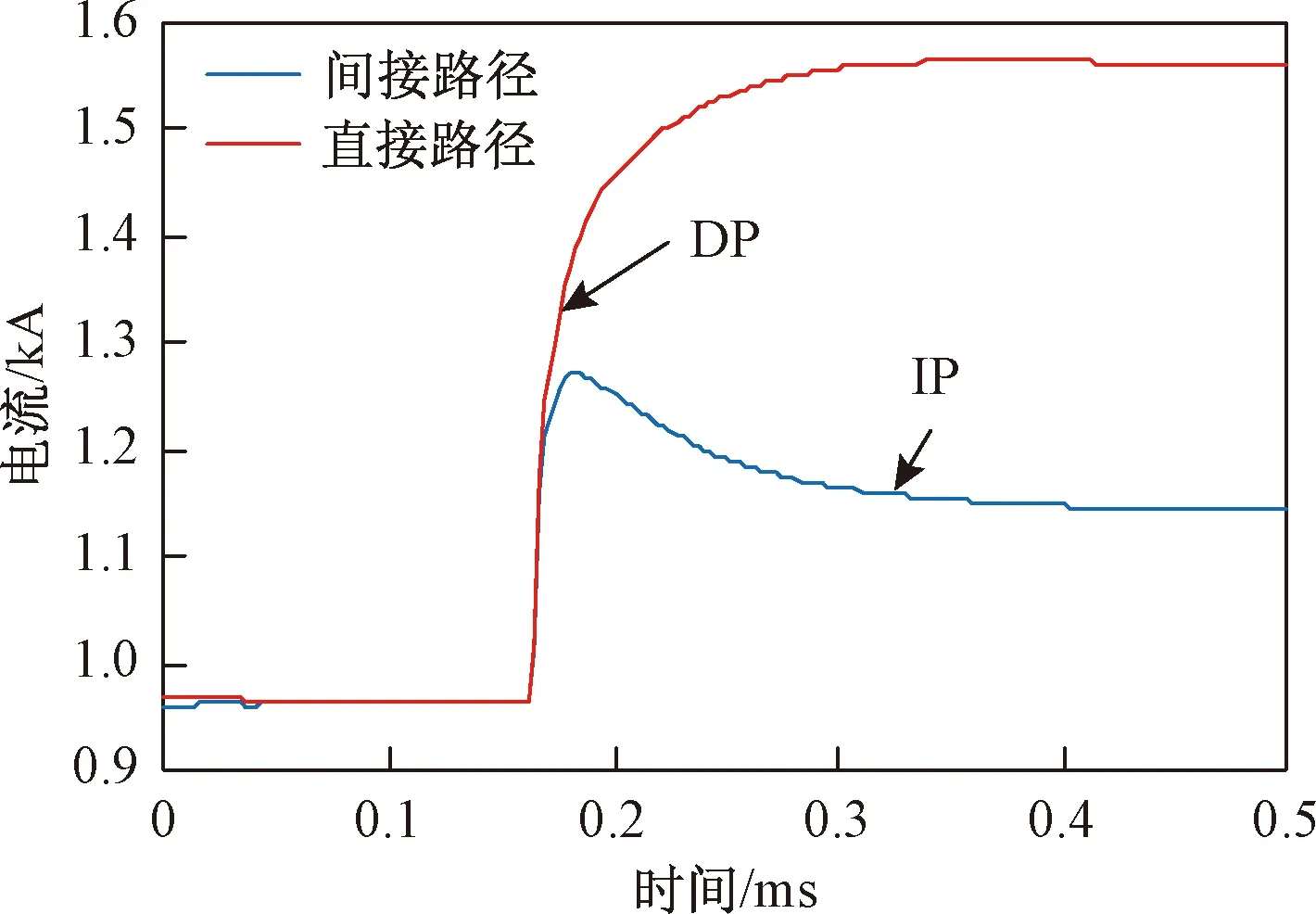
3 基于行波衰减理论的故障定位算法
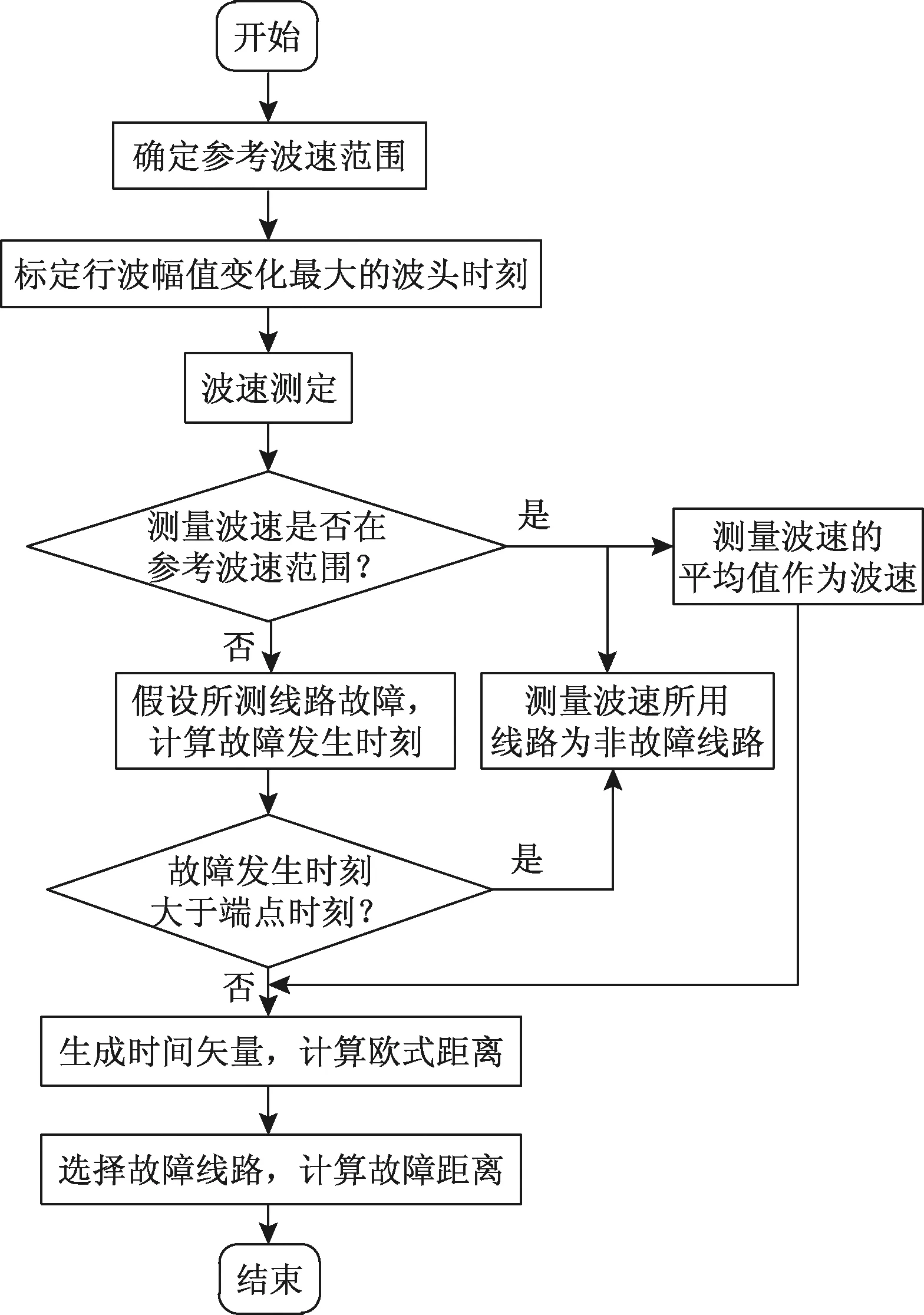
3.1 参考波速范围的确定
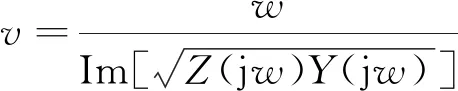
3.2 幅值变化最大波头的标定
3.3 波速测定
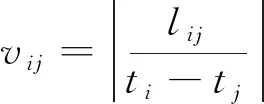
3.4 故障发生时刻的计算
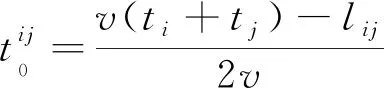
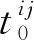
3.5 故障线路的查找
3.6 故障测距
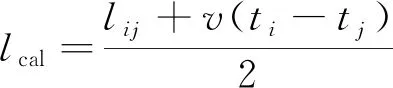
4 仿真测试及特性分析
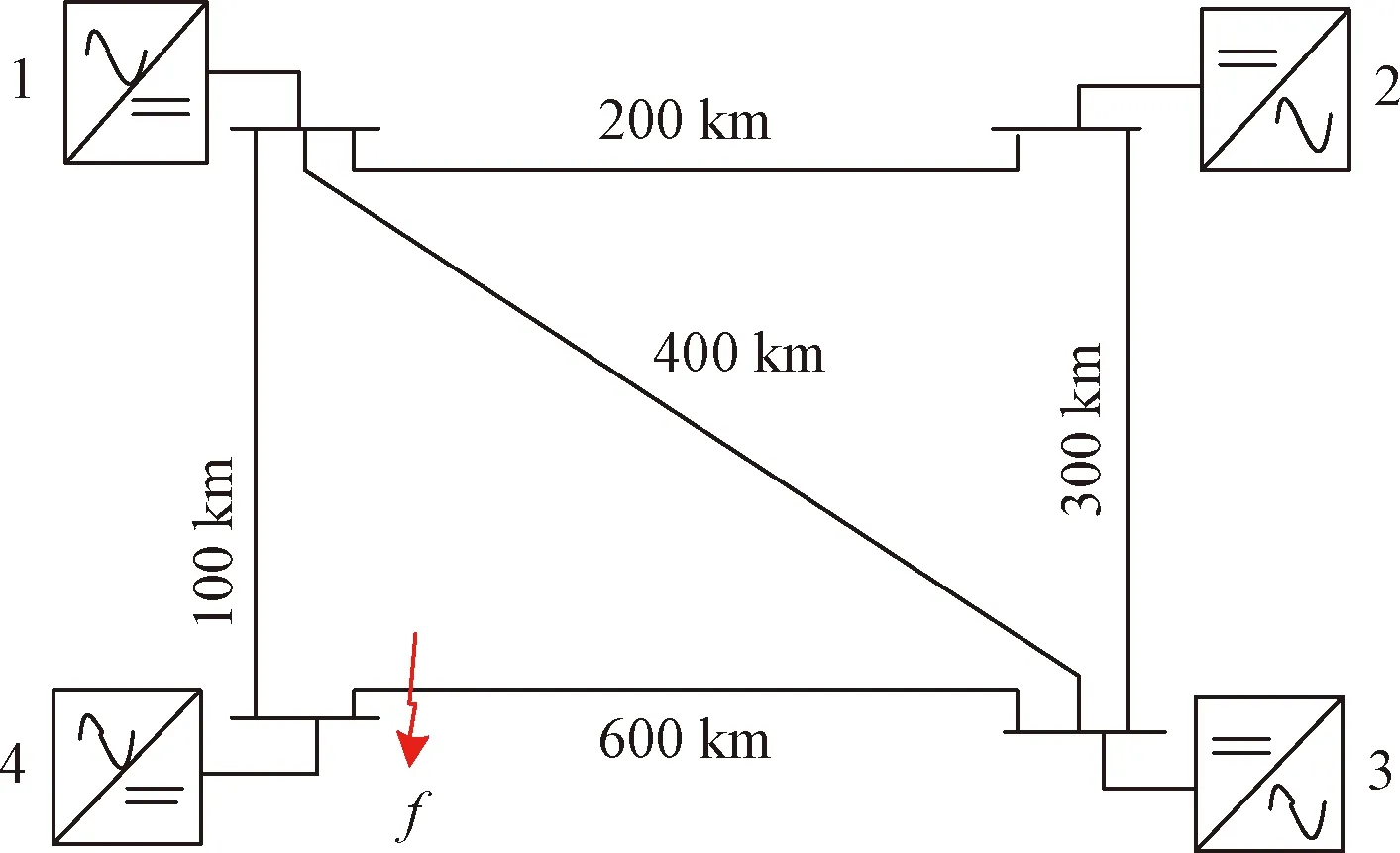
4.1 仿真测试
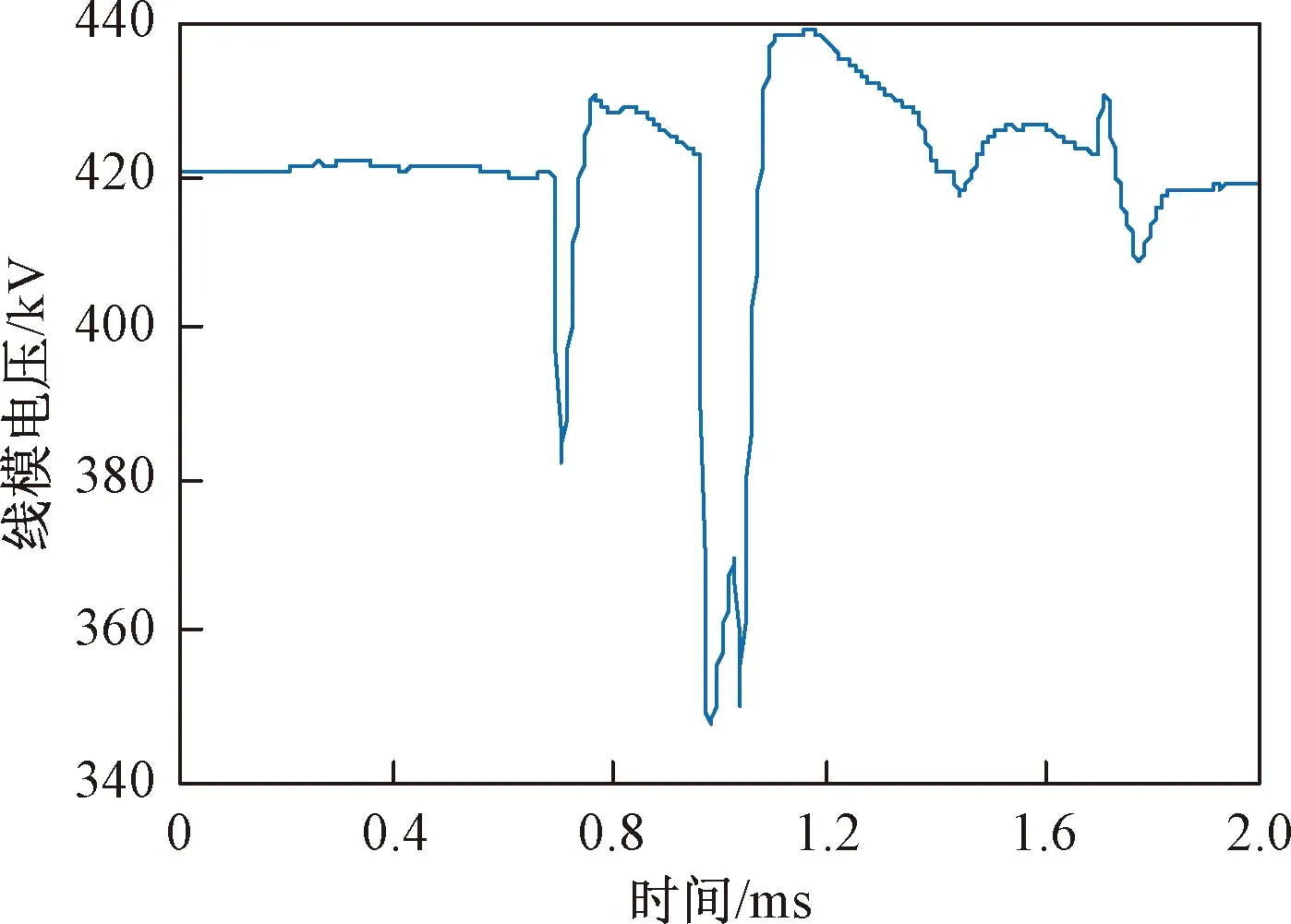
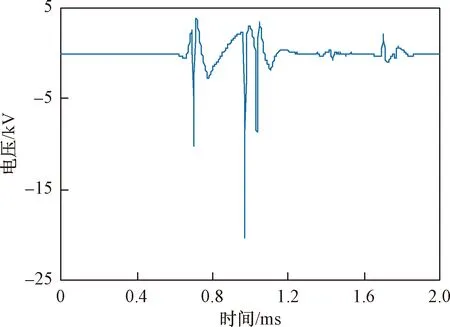

4.2 结果分析
4.3 影响因素分析

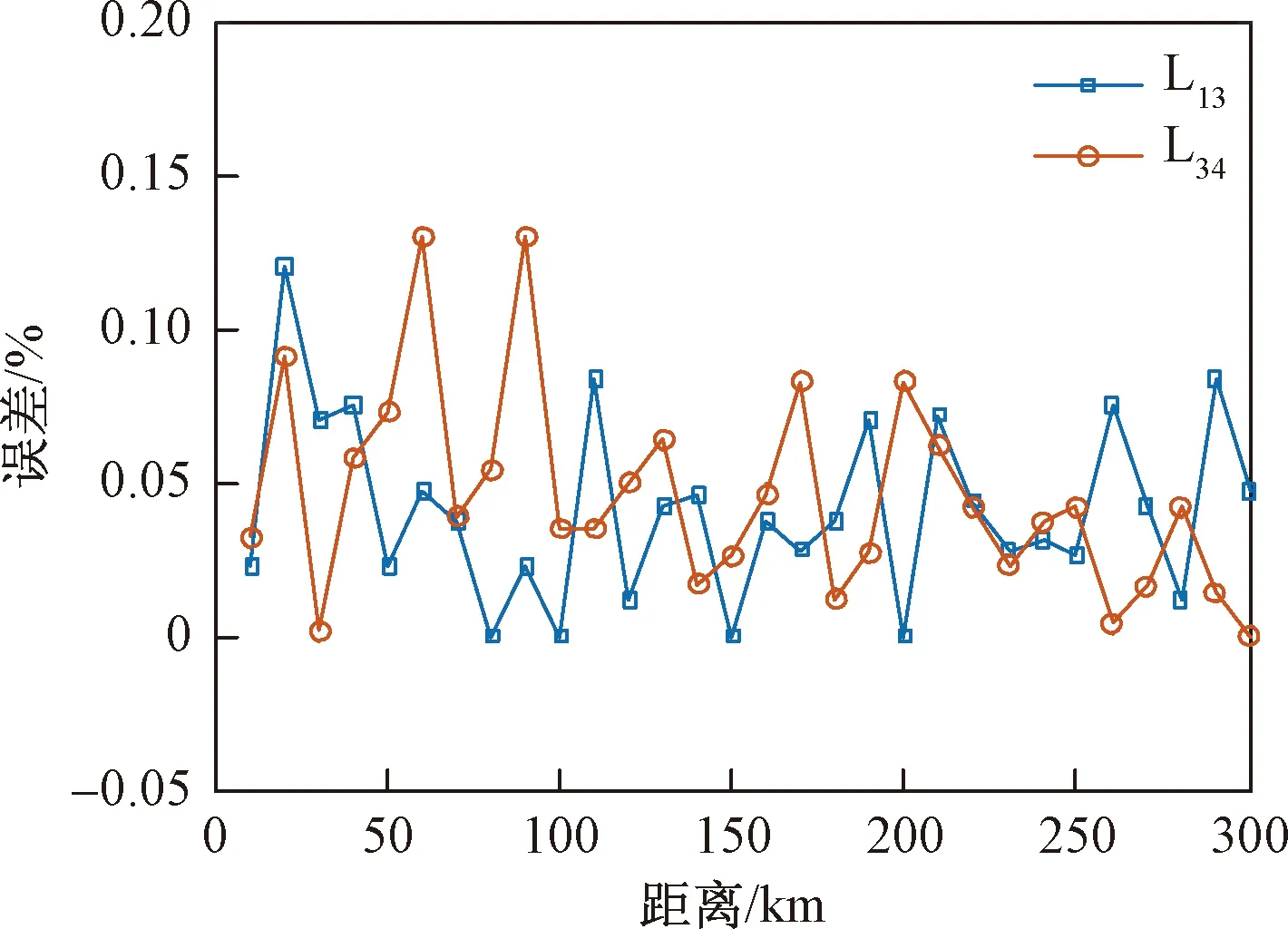

5 结论

