基于健康因子驱动的风力发电变桨系统自适应容错控制
王宏伟, 张 倩
(1.新疆大学电气工程学院, 乌鲁木齐 830047; 2. 大连理工大学控制科学与工程学院, 大连 116024)
风力发电属于分布式发电系统中的重要构成部分之一,作为清洁能源中的典型代表,此种能源的利用不需要付出严重的环境代价,可以有效规避对环境造成的污染。当前不少欧洲国家都在大力推广风电,中国也都在适合建设风力发电的区域内大量建设风电场基地。风力发电一般包含控制系统、感应发电机和传动装置等,同时也包含其他方面的设备。风力发电机在整个系统中的作用就是转化风的动能,再转化为机械能之后再转变为电能。一般而言,叶片会在风的作用下发生旋转,再在轴承及变速齿轮的作用下实现风力发电机的发电[1]。
在双馈式风电机组发电系统中,由于系统转动惯量、风机叶片质量、永磁体的磁化强度等系统本身参数的变化[2],以及元器件的老化或非正常工作等因素的影响,用原有的鲁棒方法设计的控制器可能会导致系统性能变坏甚至不稳定,系统会发生失速、转动轴严重破坏,出现故障,影响到整个系统的安全运行[3-4]。由于对于风力发电系统在野外运行时间较长,经常遇到很多极端天气、系统的自身故障和执行器内部故障。由于大型风电系统结构复杂,系统何时、何地、何处发生故障,这些都很难给予预测,同时,故障发生后又可能导致风电机组整体系统结构和控制性能发生一些变化。因此,对于大型风电机组发生故障的动态系统,如何保证系统稳定性和性能指标是控制器设计的基本问题。
可靠控制在近年来得到很多研究者的关注,提出了许多可靠控制的研究成果[5-9]。可靠控制的优点是:故障发生时,能及时地实现容错控制,特别是采用自适应容错控制,不需要故障诊断机构提供精确信息,利用自适应控制的思想,设计自适应调节律来处理在线估计诊断和控制[10-11]。自适应容错控制已在重大安全系统,如石油化工[12]、核反应堆[13]、飞行器[14]等系统中进行了应用。在这些自适应容错控制方法中,如何处理非线性系统现象仍是自适应容错控制器设计的难点问题。
现提出基于健康因子函数的模型参考自适应的容错控制方法,用以解决大型风电系统同时存在执行器故障、外界干扰和模型不确定性等非线性特性的控制问题。其核心思想是:在执行器发生故障不可控部分、含有的非线性部分、外界干扰部分,它们和函数的范数要求有界的前提下,利用健康因子函数来衡量执行器的健康状态,并将健康因子函数加入控制器中,通过李雅普诺夫稳定性定理设计自适应容错控制器。最后,通过大型双馈风电变桨系统的容错控制证明所提出方法的有效性。
1 问题的提出
考虑一类存在执行器故障和外界干扰的风力发电系统,其模型为
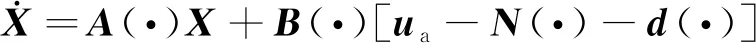
(1)
式(1)中:X∈Rn为状态变量;A(·)∈Rn和B(·)∈Rn×m为未知矩阵;N(·)∈Rm为系统中的非线性项;d(·)∈Rm为外界干扰项;ua(t)∈Rm为系统的控制信号。控制的目标是:设计一个控制器,保证闭环系统的所有信号有界。为此,采用模型参考自适应控制方式,让系统的状态向量跟踪参考模型的状态向量。对于控制的参考模型为
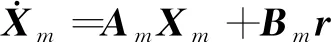
(2)
式(2)中:Xm∈Rn为参考模型的状态变量;Am∈Rn×n,Bm∈Rn×m为已知矩阵;r(t)为有界且一致连续的参考输入。
为了更好地描述执行器发生故障,引入了“健康因子函数”来描述执行器的健康状况。
定义1健康因子函数0≤ρi(t)≤1,i=1,2,…,m。用ρi(t)来表示t时刻的第i个执行器的健康状态。当ρi(t)=1时,表示第i个执行器是完全健康的;当ρi(t)在[0,1]时,第i个执行器属于亚健康状态,ρi(t)越低,则第i个执行器的健康程度越糟糕。当ρi(t)=0,第i个执行器则彻底失去工作能力。
采用健康因子函数来描述大型风电机组的健康,含有健康因子的风力发电机组可以用图1描述。
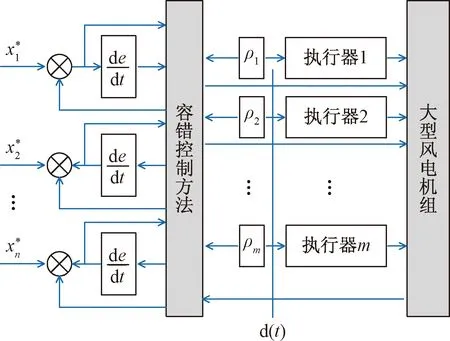
图1 含有健康因子的风力发电机组的控制结构
由于多个输入信号与多个执行器连接,可以用执行器的健康程度矩阵来表示执行器的健康情况,记为ρ(t)=diag{ρi(t)}。当执行器发生故障(如停电、部分失效或几种故障的组合)时,可以采用健康程度矩阵来表示多个执行器的健康状况,此时,被控对象实际控制输入ua(t)与所设计控制输入u(t)不再一致,它们的关系为
ua(t)=ρ(t)u(t)+υ(t)
(3)
式(3)中:ρ(t)=diag{ρi(t)},其对角元素ρi(t)为线性时变标量函数,ρi(t)∈(0,1],(i=1,2,…,m)。υ(t)为向量函数,反映执行器失效时执行器产生的不可控部分。执行器故障的几种常见类型如表1所示。

表1 执行器故障的几种常见类型
在设计控制器时,系统模型和参考控制模型之间还需要满足一些假设。
假设1系统矩阵A(·)和B(·)未知,需满足以下的匹配条件,即
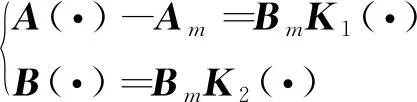
(4)
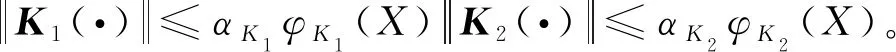
假设2矩阵C=K2ρ是正定的,并存在一个正常数λm使得式(5)存在:
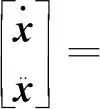
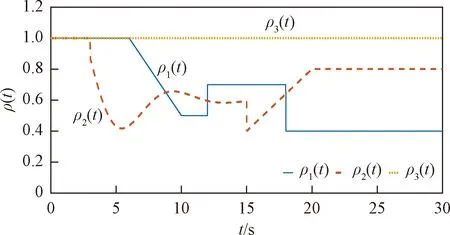
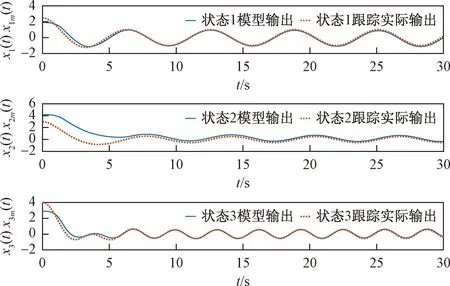
0<λm (5) 式(5)中:λi(·)为括号矩阵内的第i个特征值。 对于系统[式(1)],采用的控制器形式为 u(t)=-K0E(t)+K(t) (6) 由假设1可以得到系统误差动态方程为 AmE+[A(·)-Am]X+ B(·)[ua-N(·)-d(·)]-Bmr= (7) 根据假设1和假设3,式(7)中的L(·)可以使下列不等式成立: (8) 若α=max{1,αK1,αK2αϑ,αK2,αK2αN},就有: (9) 令: φ(·)=1+φK2(1+φN)+ (10) 那么,式(9)可写为 (11) 则就有: (12) 定理1针对式(1)的风电系统,采用式(3)含有健康因子描述的控制器。如果存在正定对称矩阵P、K0,以及常数φK2>0、φK1>0、φN>0,γ>0,并且假设1~假设3成立,采用如下公式进行控制: (13) 证明:首先,令 (14) 考虑如下Lyapunov函数: (15) 式(15)中:γ>0的常数。 式(15)对时间求导数,结合式(7)、式(9)可以得到: (16) 由式(14)和式(13)可知: (17) 令C=K2(·)ρ,当C为正定矩阵时,根据假设2就能得到: (18) 利用式(18),式(17)可整理为 (19) 由式(12)、式(19)可以进一步整理得到: (20) 根据式(13),有: (21) 因此可得出V∈L,这意味着u∈L,E∈L,当E→0状态X(t)→Xm(t)。 讨论1定理1提出的控制算法不依赖于故障的时刻、健康情况、规模或者尺寸,只要在故障、外界扰动是有界的,就能实现控制,控制算法具有一定的鲁棒性。 定理2对于式(1)的风电系统,采用式(3)含有健康因子描述的控制器。如果存在正定对称矩阵P、K0,以及常数φK2>0、φK1>0、φN>0,γ>0,并且假设1~假设3成立,设计控制如下: (22) 则能够保证系统[式(1)]的状态能够有一致有界稳定跟踪。 证明首先,考虑如下Lyapunov函数: (23) 式(23)中:γ>0的常数。 式(15)对时间求导数,并利用式(7)、式(8)、式(14)、式(22)可得: (24) 令C=K2(·)ρ,利用式(12)、式(18)可得: (25) (26) (27) (28) 将式(27)的非正项消去,从而变为 (29) (30) 考虑如下某大型风电机组的叶轮桨动态方程: (31) N(·)= d(·)∈R3为不平衡载荷、叶片弯曲、推进器、叶片升力引起的总力矩;ua(·)∈R3为实际的控制输入;JLBi(i=1,2,3)为空气加速引起的等效惯量力矩;JBIi(i=1,2,3)—转子叶片沿其纵轴的全部惯性力矩;kDBi(i=1,2,3)为阻尼系数;kRLi(i=1,2,3)为摩擦系数。 式(31)可以写为 (32) 或者写为 (33) 选择控制参考模型为 (34) 系统初始状态为X(0)=[3 1 3 0 0 0]T。在研究中,选择参考模型矩阵为A0=A1=I。执行器故障时不可控部分的控制输出为υ(t)=[0.5sinx10.2sinx20]T。3个通道执行器的健康因子函数如图2所示,其中通道3的执行器始终完好。在仿真开始时风电系统正常运行,但是外界干扰一直存在系统中。在t=3 s以后,系统通道2的执行器发生一定程度的故障,系统t=6 s以后,系统通道1的执行器发生一定程度的故障。两个通道的执行器健康因子有时低于了50%,且在整个时段,故障呈现时变状态。 在仿真中,参考模型的输入为r(t)=[4 2 3]T,xm(0)初始状态为xm(0)=[2.5 3 4]T。风机运行中两个桨距角执行器发生严重故障,健康因子平均值只在0.4左右,采用定理2提出的控制器对风电系统进行控制。图3给出了跟踪过程。 图2 风电系统中3个执行器的健康因子曲线 模型输入r(t)=[-sint0.5cost-sin2t]T,xm(0)初始状态为xm(0)=[2.5 3 4]T。采用定理2提出的控制器对系统进行控制。图4给出了跟踪过程。通过仿真可以看出,在不同输入信号下,对于执行器存在不同健康情况下,通过控制器的设计可以使系统完成跟踪任务,效果良好,简单适用。 图3 风电系统的桨距角跟踪过程 图4 风电系统的桨距角跟踪过程 通过理论分析和仿真,模型参考自适应容错方法能够解决风机发电机组模型的不确定性,外界干扰、执行器故障的非线性系统的控制问题。通过健康因子函数对执行器故障进行分析,控制设计简单、方便、适用,同时能够在系统存在不确定性、外界干扰和执行器出现故障时,根据健康因子函数的评估直接进行对系统进行自适应容错控制。健康因子函数往往不容易产生,但可以通过专家进行量化,量化后的系统可以看作是一个混杂切换非线性系统,这是今后的研究方向。
2 鲁棒自适应容错控制器的设计
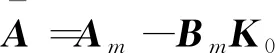
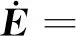
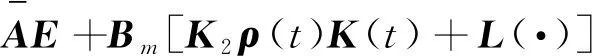

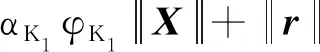

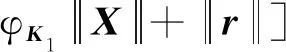
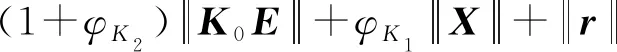


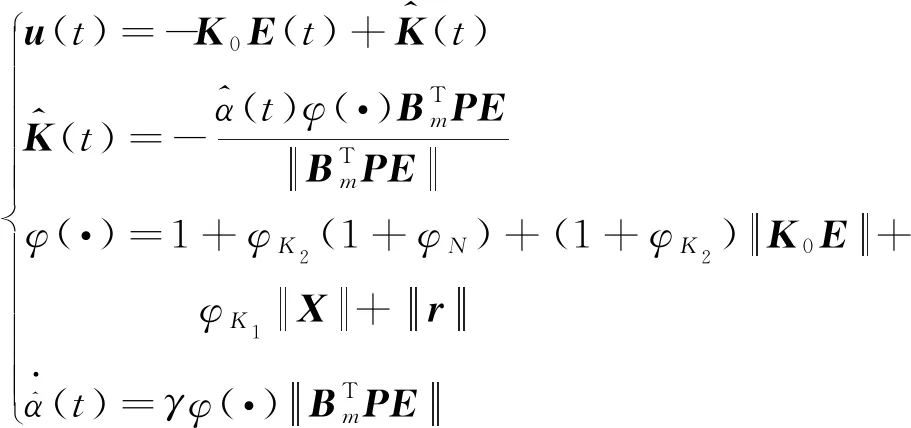
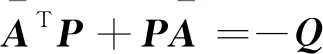
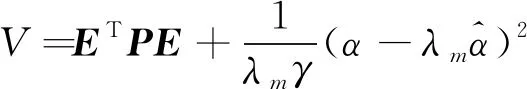
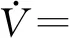
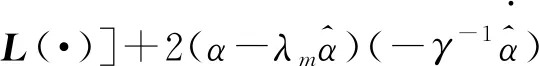

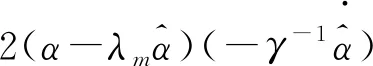
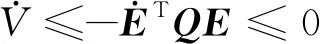
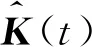
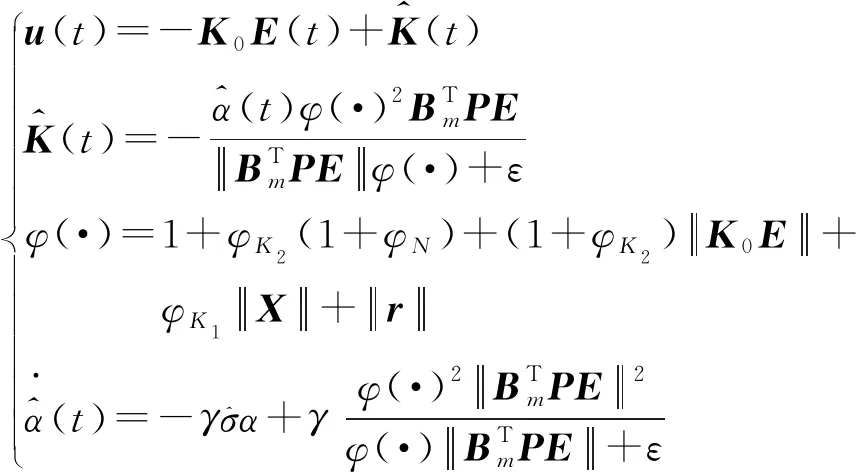
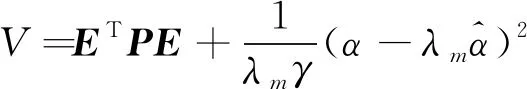
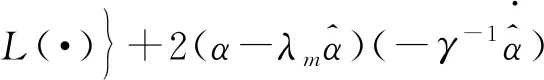
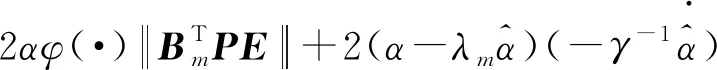

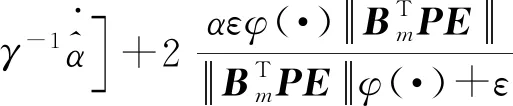
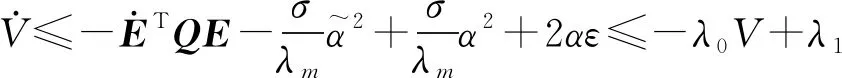


3 风电机组的变桨系统的容错控制
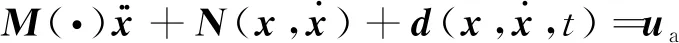
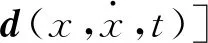
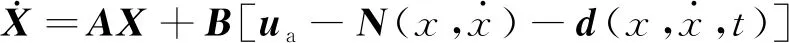
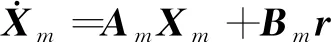

4 结论

