基于Realizablek-ε湍流模型的泵站进水池水流流态研究
陶东 周冬蒙 刘子金

摘 要:泵站进水池进水喇叭口附近因抽吸力的作用而产生大量旋涡,进而严重影响水泵吸水效率。为探究进水池内部水流流态特性,基于Realizable k-ε湍流模型对泵站进水池水流流态进行数值模拟,并与HXH03-1S型超声波多普勒流速流向仪在泵站进水池的原型监测结果进行对比,验证数值模拟结果的可靠性。在此基础上,对泵站进水池水流流动特性进行分析。结果表明:Realizable k-ε湍流模型对泵站进水池水流流态的模拟与HXH03-1S型超声波多普勒流速流向仪在泵站进水池的原型监测结果吻合度较高,表明该数学模型模拟泵站进水池水流流态具有较高可靠性;喇叭口两侧出现相反方向的涡流,与吸入喇叭口内的水流形成新的涡带,致使管道内的流态受到了前池流态的影响。
关键词:泵站进水池;Realizable k-ε湍流模型;旋涡;数值模拟
中图分类号:TV675;TV698.1+6 文献标志码:A
doi:10.3969/j.issn.1000-1379.2020.11.006
Abstract:In the vicinity of the inlet bell of the pumping station, a large number of vortices are generated due to the suction force, which seriously affects the water absorption efficiency of the pump. In order to explore the flow characteristics of the water in the inlet pool, the flow regime of the pumping station was numerically simulated based on the Realizable k-ε turbulence model and compared with the prototype monitoring results of the HXH03-1S ultrasonic Doppler flow rate meter in the pumping station inlet tank to verify the reliability of the numerical simulation results. On this basis, the flow characteristics of the pumping station inlet water were analyzed. The results show that the coincidence degree of the flow pattern of the pumping station inlet and the prototype monitoring results of the HXH03-1S ultrasonic Doppler flow rate meter used in the pumping station is high, showing that has higher reliability. The vortex in the opposite direction on both sides of the bell mouth and the water flow in the suction bell mouth form a new vortex belt, so that the flow regime in the pipeline is affected by the flow state of the front pool. The research results have important guiding significance for guiding the optimization design of the front pool of large pumping stations and the flow analysis during the structural transformation process.
Key words: pump sumps; Realizable k-ε Turbulence Model; vortex; numerical simulation
泵站是灌區最主要的建筑物,而进水前池是泵站的重要组成部分,其主要作用是引导水流平稳地进入泵站进水池,保证水泵良好的进水条件。泵站运行中,前池流态是否平稳直接影响水泵吸水管的进水流态,进水池中的水流流态对泵站提水效率及水泵的气蚀性能具有重要影响[1]。目前该领域学者针对泵站进水池内部涡流特性开展了大量研究,取得了丰富的研究成果。LI等[2]采用二维PIV系统,从PIV数据中得到流速、流线、湍流强度和涡度,通过对这些参数的分析,找出了具有特殊结构的集水池的流动特性,并在实验的基础上确定了最佳的流动条件;SUERICH-GULICK等[3]通过对进近流和涡旋内部流的速度测量,提出了一种半经验模型,粗略地预测了进近气流和进气口几何形状如何决定核心涡特性;TEMMERMAN等[4]利用大涡模拟湍流,考虑流体黏度的影响,讨论了速度分布的数值计算结果,并与ANSAR和NAKATO的实验数据进行了比较,取得了较为理想的模拟结果;JAKIRLI等[5]采用大涡模拟技术对某小型水电设施进水口三维非定常流场进行了数值模拟,基于针对自由表面流动改进的高度简化的MAC迭代法,采用近壁面阻尼修正的标准Smagorinsky模型对亚网格尺度应力进行了计算,利用数值网格对实验室尺度雷诺数的近壁面流场进行了数值求解,较好地再现了涡旋流场的复杂性和非定常性;YU等[6]首次通过对黏性子层的充分求解,对SST k-ω湍流模型进行改进,并与标准的SST k-ω湍流模型进行比较,改进后的模型对气体污染物在孤立建筑物周围的扩散模拟有很好的适用性;为保障泵站稳定、高效运行,学者们运用多种湍流模型对前池的水流流动特性进行仿真模拟,并提出了多种整流措施[7]。以上研究为泵站进水池水流流态优化提供了可靠的理论依据。但受早期测流手段的限制,前人们的研究方法主要集中在物理模型试验和数值模拟,对前池原型的测流手段较少,有针对性的泵站进水池流态理论研究尚不充分。
近年来,随着测量技术的发展,测量结果的精度已有了较大幅度的提升,泵站前池流速监测技术已经在工程建设相关领域得到了广泛应用,具有安全、高效、精度较高等优势。鉴于此,本次研究基于Realizable k-ε湍流模型对泵站进水池水流流态进行数值计算,并与HXH03-1S型超声波多普勒流速流向仪在泵站进水池的原型监测结果进行对比,验证数值模拟结果的准确性。在此基础上,对泵站进水池水流流动特性进行分析。
1 数学方法和计算模型
1.1 控制方程
1.2 边界条件设置
①前池断面尺寸以及泵站设计流量均已知,前池进口断面处平均流速可求,故选用速度进口边界条件;②出口压力和流速均未知,假定出口边界对上游水流运动无影响,水流视为完全发展流动,设置出口边界条件为outflow边界条件;③在近壁面区域,由于流体运动变化比较大,因此选用壁面函数法[8]处理固壁边界;④泵站进水前池自由表面受外部环境扰动较小,浮动变化可以忽略,同时考虑到网格划分以及对计算时间的要求,选用刚盖假定法[9]对自由表面进行模拟计算,将自由表面条件设置为symmetry。
1.3 网格划分和流场离散化
流动问题数值模拟计算的效率与精度主要取决于网格生成的质量及所采用的算法[10]。由于所选泵站侧向进水前池结构形态复杂,因此采用非结构化四面体网格进行划分,局部位置适当加密。应用Fluent软件进行浑水两相均质流模拟,基于有限体积法对计算区域进行离散化,采用二阶迎风格式的隐式求解方法以确保计算精度,并选用基于分离求解器的SIMPLEC算法进行流场耦合。
1.4 模型构建
本研究采用的泵站进水池物理模型是按照泵站前池实际尺寸1∶1构建,如图1所示。图中吸水管内径为1.6 m,泵管内流量为2.41 m3/s,喇叭口水深为6 m。管内雷诺数为75 000左右,进水池内雷诺数为10 000左右,Fr和Wb(韦伯系数)为模拟所需确定的相似准则数,其值分别为1.1和840。本研究取前池及进水池作为研究对象,采用非结构化网格进行划分,在扩散角变化处及水泵进水口附近位置进行网格局部加密,计算区域及局部细节如图2所示。研究工况是设计工况,其进口取在渠道渐变段与前池连接处,设置为体积进口,流量为8.5 m3/s。出口设置在进水池水泵进水喇叭口处,将自由表面简化为对称面并且不考虑其他表面波动。
2 模拟结果验证
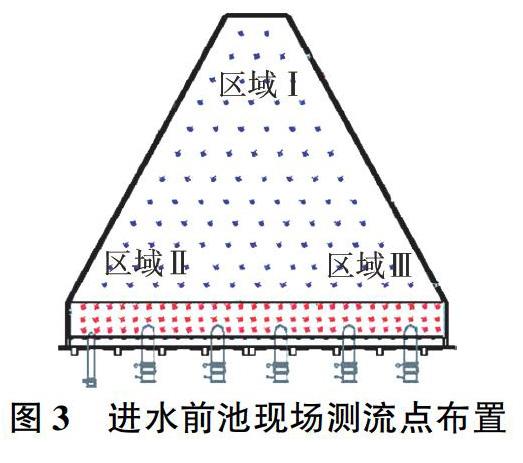
为进一步确认数值计算的准确性,本次研究对泵站前池水流流速采用HXH03-1S型超声波多普勒流速流向仪进行测量,此型号流速仪采用最先进的电子技术,具有高度灵敏性,尤其对于高含沙水流抗干扰能力强,对弱流和强流都有很好的适用性,在选定的泵站图纸上建立坐标系,先对泵站前池进行划分,选取158个测点,测点布置如图3所示,连接水下探头沿不同深度对流速进行测量,得到每个测点不同深度的流速数据,再利用Surfer等值线绘制软件绘制不同断面处的流速等值线图。
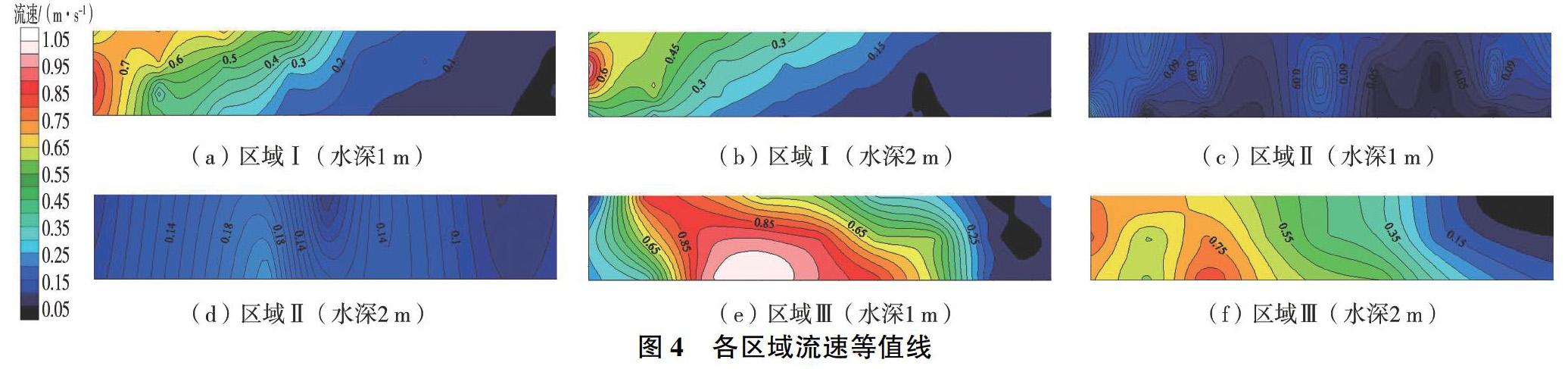
依据现场测流数据可知,各点流速范围均在0.00~1.05 m/s之间,运用Surfer软件分别绘制3个典型区域水深1 m、2 m处流速等值线图,如图4所示。图3 进水前池现场测流点布置
区域Ⅰ受运行机组影响,在各个深度左侧流速总体大于右侧流速,随着水深加大,右侧低流速区域逐渐增大直到出现静水区;区域Ⅱ侧壁处整体流速较小,且出现较多旋涡回流,整体流速变化较小,旋涡在水深1 m处集中;区域Ⅲ水流入口处流速较大,且受侧壁处旋涡的影响,主流有向左偏移的趋势,随着流速的增大低速区范围逐渐变大。由此可见,机组打开的区域水流流速大于机组未打开的区域,且受侧壁处旋涡影响主流向左偏移,与现场测流结果趋势一致。
3 结果与讨论
3.1 喇叭管下方速度分布分析
为验证Realizable k-ε湍流模型在喇叭管周围流态模拟的准确性,对喇叭口下方进行3种不同工况下的流速测量,图5按照进水流道内各个方向速度平均值对其3个方向的速度值作无量纲处理,Vx、Vy、Vz分别代表x、y、z方向上的速度,Ly为测点距喇叭口的距离。
图5(a)为3种工况(工况一、二、三的流量依次增大)条件下基于Realizable k-ε湍流模型与实测数据在x方向的速度分布对比,可以看出,Vx模拟值与实测值变化趋势一致,随着流量增大,在近壁处的速度梯度也随之增大,而在非近壁区域随工况变化沿x方向速度分布出现一定的波动性,但整体来说3种不同工况下沿x方向的速度分布呈现出相似的趋势;图5(b)为y方向的速度分布对比,沿着y方向速度呈现的趋势为由正到负先增大后减小,其位置分别对应喇叭口测线的两侧,速度最大值出现在Ly的三分之一处,最小值出现在四分之三处;图5(c)为z方向的速度分布,在此方向3种不同工况下速度分布都呈现出相同的变化趋势,在壁面两侧因壁面效应出现了速度降低的现象。总的来说,基于Realizable k-ε湍流模型數值模拟与实测数据在3种不同工况条件下3个方向上均呈现相似的趋势,吻合度较高。
3.2 水流流动特性分析
图6、图7分别为平行水流方向和垂直水流方向的平面流速分布。水流在整个前池中均有涡流产生,主要分成3段:靠近进口端,涡流分布在进水口两边侧壁,涡流旋转方向主要是切向水流方向翻转带动向前,涡带较长;靠近前池中部的位置,涡带位于取水前池的中下部,涡带逐步缩短,表面流速较为均匀;前池尾部的涡带主要分布在表面,受到侧墙反射回来的水流的干扰,涡带水流方向呈现出周期性。在各个泵取水喇叭口对应的位置上呈现出一定速度的涡,涡的位置偏离取水喇叭口的正前方,沿着水流方向,在两台泵取水喇叭口中间位置也出现了涡流,涡流的主要方向是顺着水流方向向前,且涡带较长,沿着水流方向,涡带的长度在缩短变宽,沿着四周旋转。沿着水流方向在喇叭口左端涡流方向向上,右端涡流向下,呈现出喇叭口两侧的水流存在搓动现象,与进入喇叭口的水流进行了较明显的切向旋转状态的流动,生成新的涡带,该类涡带在喇叭口右前方扩大并拓展到水流的表面,喇叭口周围产生的涡带沿着侧向前池的宽度方向减小。水体的流动在喇叭口前端产生了不均匀的涡带,涡带的旋转方向不确定,在靠近前池末端的机组管道的前池中相互掺混顶托向上翻滚,在前池前端入口处的机组的水中涡顺着入流方向倾斜旋转,对前池未放置进水管的侧墙产生二次冲击,形成新的不规则的涡流,进而影响取水口取水,在取水口底部交汇出现涡流分布,旋涡产生区域随着工况变化而变化,也显示出一定的动态性和不间断性,影响到水泵前端取水引流管道,致使管道内的流态受到了前池流态的影响。
4 结 论
(1)与HXH03-1S型超声波多普勒流速流向仪实测数据对比,基于Realizable k-ε湍流模型对泵站进水池水流流态的模拟在数值上存在一定差异,但整体变化趋势一致,表明该数学模型模拟精度较高,模拟结果可以很好地反映出进水前池的水流流态。
(2)喇叭口两侧出现方向相反的涡流与吸入喇叭口的水流形成了新的涡带,对前池未放置进水管的侧墙产生二次冲击,在取水口底部形成新的不规则的涡流进而对喇叭口管道内部流态产生影响,表明当进水池结构尺寸设计不当时,侧壁撞击形成的旋涡危害是不可忽视的。
(3)对泵站进水池的数值模拟会略微高估进水池边壁处的流速,主要原因是进水池两侧水流流速较中间部位小,导致大量泥沙淤积,而模拟过程中未考虑泥沙浓度对水流黏滞性的影响。对于高含沙水流的模拟是复杂的、多维的,高含沙水流颗粒间的相互作用以及水沙两相的相互作用对进水池流态模拟有一定影响,后续研究将主要集中在这一领域。
参考文献:
[1] 高传昌,曾新乐,解克宇,等.泵站进水池超低水位下组合整流方案与验证[J].农业工程学报,2017,33(23):101-108.
[2] LI Y, WU Y, MANSA K, et al. The Flow Research in an Open Type Sump by PIV Experiments[C]//ASME Proceedings of ASME Heat Transfer/Fluids Engineering Summer Conference. New York:ASME, 2004:5-12.
[3] SUERICH-GULICK F, GASKIN S J, VILLENEUVE M, et al. Free Surface Intake Vortices: Theoretical Model and Measurements[J].Journal of Hydraulic Research, 2014, 52(4):502-512.
[4] TEMMERMAN L, HADIABDI M, LESCHZINER M A, et al. A Hybrid Two-Layer URANS-LES Approach for Large Eddy Simulation at High Reynolds Numbers[J].International Journal of Heat and Fluid Flow, 2005, 26(2):173-190.
[5] JAKIRLI S, KADAVELIL G, KORNHAAS M, et al. Numerical and Physical Aspects in LES and Hybrid LES/RANS of Turbulent Flow Separation in a 3-D Diffuser[J]. International Journal of Heat and Fluid Flow, 2010, 31(5):820-832.
[6] YU H S, JESSE T. Simulation of Gaseous Pollutant Dispersion Around an Isolated Building Using the k-ω SST (Shear Stress Transport) Turbulence Model[J]. Air Repair, 2017, 67(5):517-536.
[7] CONSTANTINESCU G S, PATEL V C. Numerical Model for Simulation of Pump-Intake Flow and Vortices[J]. Journal of Hydraulic Engineering, 1998, 24(2):123-134.
[8] 資丹,王福军,陶然,等.边界层网格尺度对泵站流场计算结果影响研究[J].水利学报,2016,47(2):139-149.
[9] 陆林广,刘军,梁金栋,等.大型泵站出水流道三维流动及水力损失数值计算[J].排灌机械,2008,26(3):51-54.
[10] TRAN T T, KIM D H. A CFD Study into the Influence of Unsteady Aerodynamic Interference on Wind Turbine Surge Motion[J]. Renewable Energy, 2016,90(5):204-228.
【责任编辑 张 帅】

