谈求分式型函数最值(或值域)的解法

◇ 湖北 何红星

(作者单位:湖北省襄阳市第三中学)

同学们在求函数最值或值域时,会遇到各种各样的分式型函数.不同类型的分式型函数求最值或值域需要采用不同的方法,但各题型之间又不是孤立的,是有着密切联系的.只要我们掌握其联系和规律,就可以很轻松地在各题之间进行转化.本文将对分式型函数的各种转化方法进行总结.

题型1当a1＝a2＝b1＝c2＝0时,分式型函数为(其中分子是常数,分母中x 的最高次数为1次).

例1求函数x∈[－2,0)∪(0,1]的值域.

图1

题型2当a1＝a2＝b1＝0时,分式型函数为y＝(其中分子是常数,分母中x 的最高次数为1次).

例2求函数0]的值域.

题型 3当a1＝a2＝0时,分式型函数为y ＝其中分子、分母中x的最高次数都为1次).

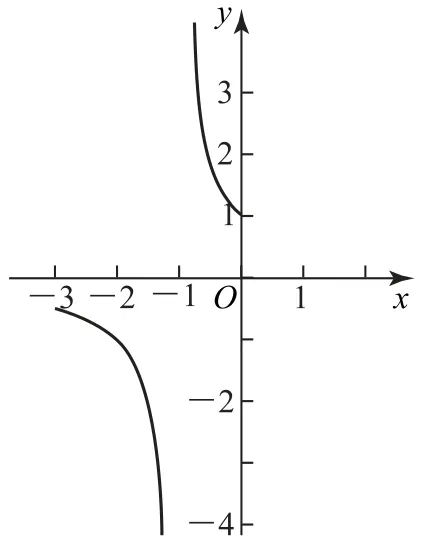
图2

例3求函数y ＝(－1,0]的值域.

(分离常数法)对于分子、分母x 的最高次数为1次的分式函数,通过分离常数可以把分子化为常数,从而可以把题型3转化为题型2.

题型 4当a2＝0 时,分 式 型 函 数 为y ＝其中分子中x 的最高次数为2次,分母中x 的最高次数为1次).

例4求函数的最小值.

(换元法)对于分母x 的最高次为1次、分子x 的最高次为2次的分式型函数,解题方法是对分母进行换元,通过换元简化函数解析式.

令x－1＝t＞0,则x＝t＋1,那么

综上,当x＝2时,函数的最小值为2.

题 型 5当 a1＝0 时,分 式 型 函 数 为 y ＝其中分子中x 的最高次数为1次,分母中x 的最高次数为2次).

例5求函数的最小值.

该分式函数的分母最高次数是2次,分子最高次数是1次.解决方法是把分子和分母同时除以分子就可以变为此时求最大值问题就变成了解决例4的问题了.

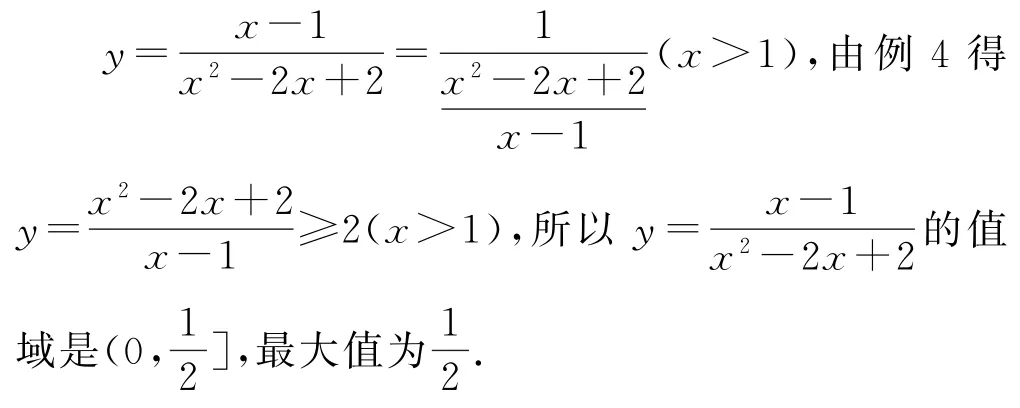
题型6当a1≠0且a2≠0时,分式型函数为y＝(其中分子、分母中x 的最高次数都为2次).

例6求函数的值域.

对于分子和分母x 的最高次项都为2次的分式函数,先通过分离常数法把分子变为最高次为1次的分式函数,就可以按照题型5的方法解决了.

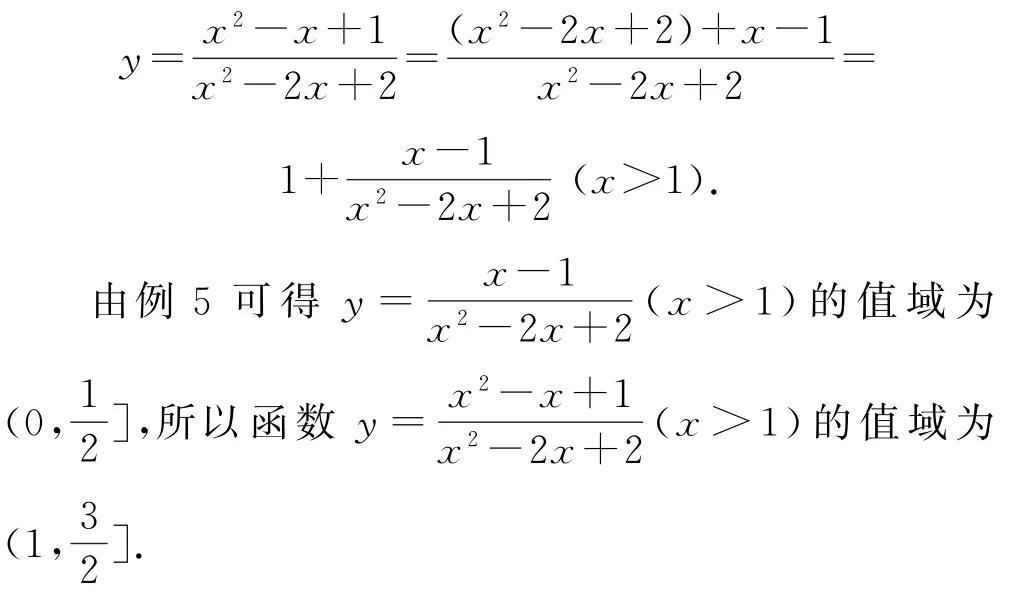
转化与化归思想在数学解题中的作用很大,它可以把难题一步一步变成简单题,分式型函数就是一个很好的例子.分式型函数各式各样、变幻莫测,但只要掌握了其变化规律和内在联系,纵然其有七十二般变化,也“逃不出我们的手掌心”.我们只要坚持由繁到简、由未知到已知进行转化,题目解决起来就很容易了.题型6通过分离常数可以转化成题型5,题型5将分子、分母同时除以分子就可以转化成题型4,变为题型4以后可以通过换元法化简,再用均值不等式或函数求导就可以解决问题.题型3可以通过分离常数法转化为题型2,题型2可以由题型1通过平移转化得到.因此,只要掌握了题型1和题型4,所有的分式型函数的最值(或值域)问题都可以得到解决.