基于光场偏振特性的目标表面漫反射分量获取技术*

蔡玉栋 韩平丽 刘飞3) 闫明宇 邵晓鹏3)†

1) (西安电子科技大学，西安市计算成像重点实验室，西安 710071)

2) (西安电子科技大学物理与光电工程学院，西安 710071)

3) (西安电子科技大学，先进光学成像前沿交叉研究中心，西安 710071)

针对三维成像、图像匹配及模式识别等领域中目标表面镜面反射光成分影响所导致成像效果受限、特征识别准确度低等问题, 提出一种基于光场偏振特性的目标表面漫反射光分量获取技术. 该技术通过对反射光场中镜面反射与漫反射分量的偏振特性进行深入挖掘, 充分利用各分量之间的偏振差异性及彼此独立性的特点, 建立线性约束模型; 此外, 通过确定线性约束模型的最佳混合系数矩阵, 实现复杂反射光场中对漫反射分量的精确获取和解译. 仿真与真实场景数据处理结果表明, 该技术能够有效地分离复杂光场中的漫反射光分量, 解决了目前三维成像及模式识别技术中对纯漫反射条件的依赖, 为被动式远距离三维成像技术在复杂反射光场中的应用奠定基础.

1 引 言

目前, 在物体表面三维形貌复原技术及图像匹配、模式识别技术[1−6]中, 为提升算法普适性, 通常假设探测器所接收到的为完全漫反射光. 然而,由于自然界中的绝大多数物体表面反射光场中镜面反射分量的存在导致以上技术的重建精度大幅降低. 因此, 全面深入分析反射光场特性, 对无先验的目标镜面反射分量与漫反射分量分离技术进行研究, 是一项很有意义又亟待解决的问题.

长期以来, 为了去除反射光场中的镜面反射分量, 精确获取漫反射分量, 国内外学者们进行了大量研究. 早在1985 年Shafer[7]基于反射光强度特性提出双色反射模型来对物体表面镜面反射光与漫反射光进行有效分离. 随后Klinker 等[8,9]在RGB颜色空间中进一步深入研究了双色反射分布模型,得到漫反射像素和镜面反射像素成斜“T”形分布,并用主成分分析法去除单张彩色图片中的镜面反射光. 然而, 受实际物体表面粗糙程度、几何形状[10]以及噪声等原因的影响, 提取到斜“T”形是很困难的, 因此降低了该算法的适用性. Tan 等[11]在把像素点投影到最大亮度-色度空间时发现, 同种颜色只含漫反射的像素点成竖直直线, 含有镜面反射的呈倒弧形, 于是提出了无镜面反射(specular-free,SF)图, 并成功地分离了漫反射分量和镜面反射分量. Shen 和Zheng[12]与Ren 等[13]在Tan 的基础上提出改进的SF 图(modified specular-free, MSF),通过将图像像素分类成簇, 利用最大光强值和光强范围值之间的比来计算图像像素点的镜面反射含量, 由于具有相同光强度比的像素可能具有不同的漫反射色度, 因此该方法会损失图像纹理特征.Sato 和Ikeuchi[14]通过在移动光源下采集图像序列的颜色成分来计算镜面反射光, 并得到了较好的结果. 但实际成像中光源方向的限制导致该方法的应用大幅受限.

随着探测技术的成熟, 光场多维物理特性的获取和解译能力的提升使得对光波偏振特性的利用得到了长足进步. 与传统的强度成像技术相比, 偏振成像技术凸显目标的能力更强, 更具有优势. 因此Wolff 和Boult[15]在针对面型测量技术中, 引入偏振技术, 将物体表面的反射光成分进行分类, 提出菲涅耳反射模型, 在忽略漫反射部分偏振特性的前提下, 首次利用偏振片实现了黑白图像中的镜面反射分量和漫反射分量的分离. Nayar 等[16]改进了这种方法, 将色彩信息和偏振信息结合来对反射光进行分离, 该方法虽然具有较高的算法鲁棒性,但对获取的多个偏振子图像的每一个像素点进行偏振参数拟合的这一迭代过程却大幅降低了算法的时效性. Umeyama 及Godin[17]在Wolff 的基础上, 研究得出漫反射和镜面反射分量在图像形成过程中是同时存在的, 通过旋转偏振片采集多幅高反射率物体表面图像, 得到采集图像中含有恒定漫反射分量和不同强度的镜面分量, 利用漫反射和镜面反射分量的独立性构建价值函数, 通过最小化价值函数来分离反射分量. 上述所有基于偏振技术的反射分离方法都建立在漫反射光为完全非偏振光的假设之上, 而由于实际探测时漫反射光具有一定偏振特性[18], 这就导致目前的分离方法的适用性受限.

针对以上问题, 本文提出一种更具普适性的基于光场偏振特性的目标表面漫反射分量获取技术,在无光源色度、方向及图像颜色信息等先验知识的前提下, 充分考虑目标反射光场中漫反射与镜面反射分量的部分偏振特性, 利用其偏振特性的唯一性及差异性建立线性约束模型, 并求解满足该约束的最佳分量混合系数, 提取目标表面反射光的漫反射分量. 仿真及真实场景数据处理结果表明, 该分离方法不仅有效地实现了镜面反射与漫反射的分离,而且具有良好的算法鲁棒性.

2 反射光偏振特性分析

由光场传输理论可知, 物体表面反射光由于表面粗糙度、反射率等因素的影响, 会产生不同的反射成分. 1991 年Wolff 和Boult[15]在深入分析了物体表面的影响因素后, 结合Fresnel 定律对非朗伯体表面反射光成分进行了详细的四类划分, 如图1 所示. ①光束在远大于入射光波长尺寸的平面经过单次反射而形成的镜面反射光; ②光束在物体表面的多个微面元产生多次(≥ 2 次)反射, 然后重新返回到入射介质中的反射光; ③光束在介质界面先进入到物体内部, 通过物体内部微粒之间相互作用后, 最终折射进入到入射介质中的反射光;④光束在遇到尺寸与其入射光波长在同一个量级的细小微小面元而产生的衍射光.

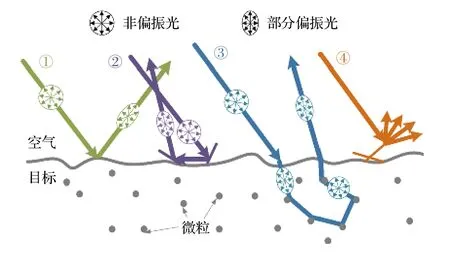
图1 物体表面反射光分类Fig. 1. Classification of reflected light on the reflection surface.

图1中①所描述的反射成分, 即通常所说的镜面反射光, 是在入射光的波长尺寸远小于物体表面的尺寸时候形成的, 这种光具有极强的方向性, 通常只能在特定的方向才能够观察到, 与②中的成分一起, 它们构成人眼看到物体表面的高光部分, 其颜色与光源颜色一致. 对于光滑物体来说, 一次镜面反射光成分较多, 物体局部反射亮度高, 高光范围窄; 对于粗糙物体, 多次反射光成分较多, 物体高光部分亮度较低, 高光范围也较宽. 通常情况下,④中描述的反射光需要物体表面具有波长尺寸量级才会发生, 所以大多数情况下它的存在极少, 可以忽略. ③属于漫反射光, 反映了物体对入射光的散射和吸收作用, 对于人眼来说, 可以通过它来区分物体的颜色信息, 同时由于它在进入到物体表面之后经过物体内部微粒的散射然后再次折射进入到空气当中, 带有物体丰富的表面形状信息, 而且其方向性没有镜面反射强, 探测起来更为方便, 所以经常被选来用作三维形貌复原. 也常被用在诸如图像分割、图像识别与匹配等大多数计算机视觉中.

此外, 光在传播过程中, 在不考虑吸收和色散等能量损耗的情况下, 入射光经过介质表面的反射与折射就只是能量重新划分的过程, 入射光能量按照一定的比例分别进入到反射光和折射光之中. 由于任意偏振态的光均可以分解为两个相互垂直的分量, 一般是把它分解成平行入射面的p 分量和垂直于入射面的s 分量. 假设界面上的入射光、反射光和折射光同相位, 则根据菲涅尔定律可知平行和垂直分量的菲涅耳系数如下式所示:

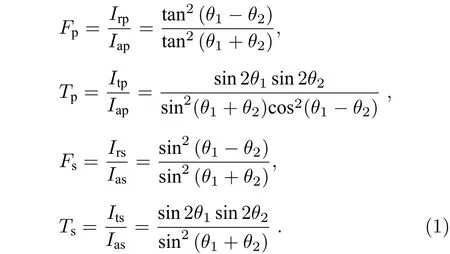
其中Iap,Ias分别是平行于和垂直于入射面的入射光强;Irp,Irs分别是平行于和垂直于入射面的反射光强;Itp,Its分别是平行于和垂直于入射面的透射光强;θ1与θ2分别是入射角及折射角. 当非偏振光照射到物体表面时, 由于菲涅耳系数的差异性导致反射光和透射光均具有一定的偏振特性. 此外, 由Wolff 的反射模型可知, 在入射面上一次或多次反射的镜面反射光呈现出与入射角相关的部分偏振特性, 同理可知, 漫反射光虽然在物体内部经历了一次完全退偏过程, 但再经过一次透射回到空气中时, 具有只和出射面形状相关的部分偏振特性. 而目前的反射分离方法中为计算简便, 通常忽略漫反射光的部分偏振特性, 将其视为完全非偏振光进行处理[15−17], 这在一些特定情况下是可行的, 但不具有普适性. 因此, 本文考虑漫反射光的部分偏振特性, 利用其与镜面反射光彼此独立的性质, 通过偏振相机采集四幅标准偏振子图像, 并能够将反射光光强表示为如下形式:

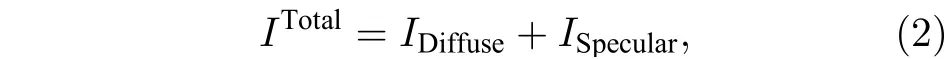
其中ITotal是总光强图像;IDiffuse和ISpecular分别是目标表面漫反射和镜面反射强度图像; 由于镜面反射与漫反射成份中偏振方向的差异性, 设fd(φi) 和fs(φi) 为相应的调制函数, 均为偏振片旋转角度φi的函数. 因此, 对于偏振方位角图像的强度Ii则应为fd(φi)IDiffuse+fs(φi)ISpecular. 而对于完全非偏振光部分, 由于其旋转偏振片过程中强度的不变性, 强度为最小透射光强Imin的2 倍.

3 漫反射成分获取模型

通过第2 节对反射光的偏振特性进行分析可知, 探测器接收到的光强是由具有完全偏振特性的漫反射光、镜面反射光及完全非偏振光三部分组成, 如(2)式所示. 如果不考虑完全非偏振部分, 则经过偏振片后获得的目标表面反射光强是相互独立的镜面反射分量与漫反射分量偏振部分的线性和[7]. 在信号处理领域, 独立成分分析就是一种用于将多元信号分离为加性子分量的计算方法. 它是在盲信号分离的研究过程中出现的一种新兴的、功能强大的非线性数据分析方法, 该方法着眼于数据间的高阶统计特性, 其本质是在源信号和混合参数均未知的前提下, 仅依据源信号的一些基本统计特征, 由混合信号恢复出源信号[19−22]. 假设m个随机观测向量x1,x2··· ,xm是由n个未知的独立分量s1,s2··· ,sn线性组合而成的, 则独立成分分析的数学模型可以表示为

其 中X=[x1,x2··· ,xm], R=[s1,s2··· ,sn] ,M为m×n的混合矩阵,M和R是未知的. 独立成分分析解决的基本问题就是根据对R的一些先验知识和随机观测向量xi来估计M和R. 据此, 可以利用独立成分分析的这种架构来对目标表面的反射成分进行分离.

Wolff 在文献[15]中提到,Imax-Imin的差值表示线性偏振反射光的大小. 最小透射辐射Imin是反射光中的非偏振分量的一半, 可以用Imin来消除(2)式中完全非偏振光成分, 建立镜面反射分量与漫反射分量的线性约束关系. 考虑到采集有四幅偏振子图像, 在去除完全非偏振光成分后, 通过行扫描将偏振子图像矩阵矢量化为行向量xj,j=1,2,3,4, 用新的观测矩阵X来表示. 同时将镜面反射分量与漫反射分量在不同偏振角度下得到的线性方程矩阵化, 得到如(4)式所示线性约束模型,其中矩阵M表示所有偏振子图像对应线性方程组的系数矩阵, 矩阵R对应的两个元素和分别是矢量化的反射光场中偏振部分的漫反射分量和镜面反射分量.

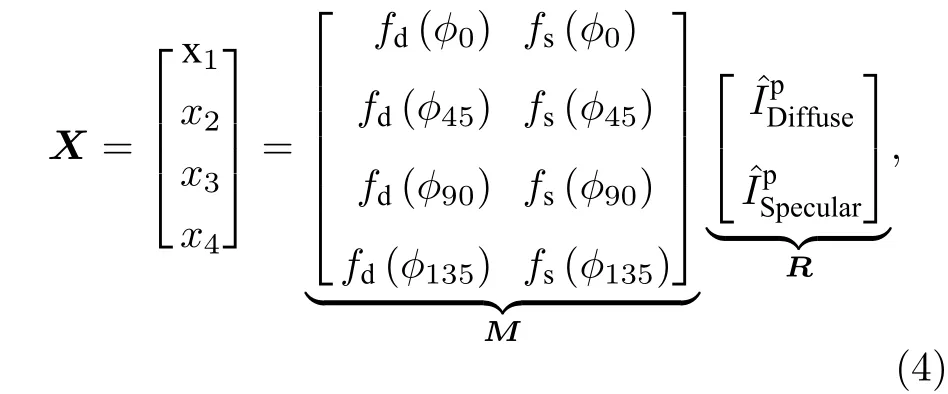
因此, 镜面反射与漫反射分离的问题就转化为对线性约束模型中的观测矩阵X进行最优分解的问题. 在旋转偏振片采集不同光强图像时, 漫反射的完全偏振部分的透光轴方向被选作φ0方向, 考虑到镜面反射光与漫反射光的透光轴不在同一个位置, 根据马吕斯定律, 矩阵M的第一列元素为fd(φ0)∗[1;1/2;0;1/2]. 考 虑到fd(φ0) 是 一个 常 数,它只影响图像整体的亮暗, 不影响矩阵的分解结果, 为求解方便假设其值为1. 此外, 由于矩阵M和R的秩是2, 所以它们的乘积矩阵的秩也为2.因此, 我们用一个秩为2 且易分解的矩阵来近似X, 并把它按需求分解成两个矩阵的乘积.

(3)鼓励企业实行公司制改制，国企混改、民企股改，加快产业转型升级。把科技创新落实到产业转型升级上，聚焦新能源新材料等新兴产业领域，加快技术引进和创新成果推广应用，提升产业核心竞争力。

由于矩阵X( 4×n阶,n＞4 )是任意的, 把任意矩阵的奇异值按从大到小的顺序排列后, 容易发现, 奇异值衰减迅速, 其前10%甚至前1%的奇异值的和已经占了全部奇异值和的99%以上[23−25].据此为了匹配秩为2 这个条件同时减少计算量, 在这里采用奇异值分解(SVD)的方法, 用一个秩较小的矩阵逼近一个矩阵并将其分解为两个矩阵的乘积. 将X的奇异值分解表示为X4×n=U4×4Σ4×4(VT)4×n, 其 中U是4 × 4 阶 酉矩阵;Σ是4 × 4 阶非负实数对角矩阵;VT即V的共轭转置,V是n× 4 阶酉矩阵. 引入一个任意的2 × 2非奇异矩阵W矩阵, 则最终期望的分解如下式所示:

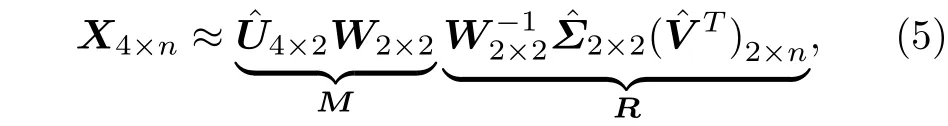
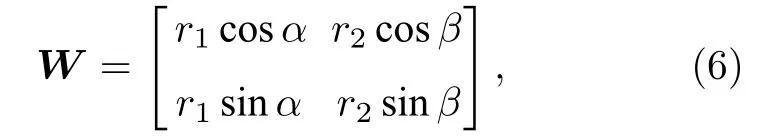
其 中r1和r2都是正实数, 且r1和α的值可以通过M矩阵的第一列元素求得. 同时考虑到W的行列式为∆=r1r2sin(β-α),∆的绝对值对应于镜面反射图像的缩放. 因此, 为了不失一般性令∆=1 ,考虑β,r2＞0,逐步改变β∈[0,π] 并利用R=计算漫反射和镜面反射图像.为了实现准确分离, 采用互信息MI (mutual information)来衡量漫反射光部分和镜面反射光部分之间的相关性[26]:

其中m和n分别为漫反射光图像和镜面反射光图像的灰度级; p rob(m,n) 表示联合概率分布函数; p rob(m) 和 prob(n) 通常为边缘分布函数. 根据互信息的定义, 当互信息取最小值时, 漫反射和镜面反射光之间相关性最低, 利用此时得到的W矩阵去求解,R中分离出的漫反射分量将不再包含镜面反射分量, 然后根据Imin的灰度直方图分布, 利用镜面反射光强明显大于漫反射这一物理规律, 寻找波峰位置所对应最高的灰度级作为阈值, 小于该阈值的光强保持不变, 大于该阈值的光强赋值为该阈值, 得到非偏振部分的漫反射光强值, 结合得到通常意义上的完整漫反射光强值, 最终实现二者的最佳分离效果.

4 实验结果及分析

为验证基于光场偏振特性的目标表面漫反射与镜面反射分离方法的有效性, 根据Lambert 漫反射模型和Torrance-Sparrow 镜面反射模型分别对实验仿真得到的人脸数据进行渲染, 得到表面是漫反射光和镜面反射光的仿真结果如图2 所示.

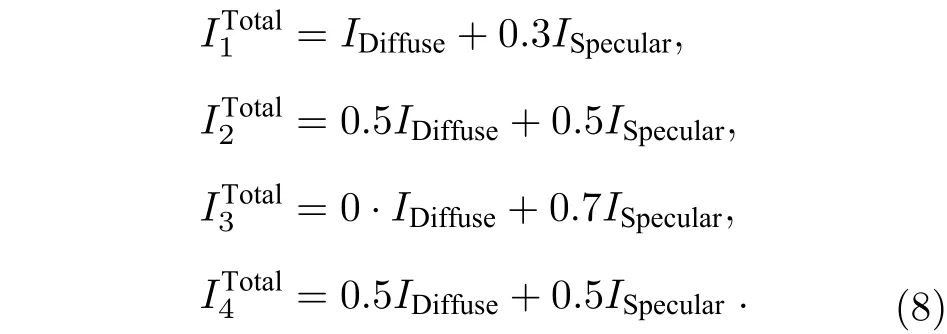
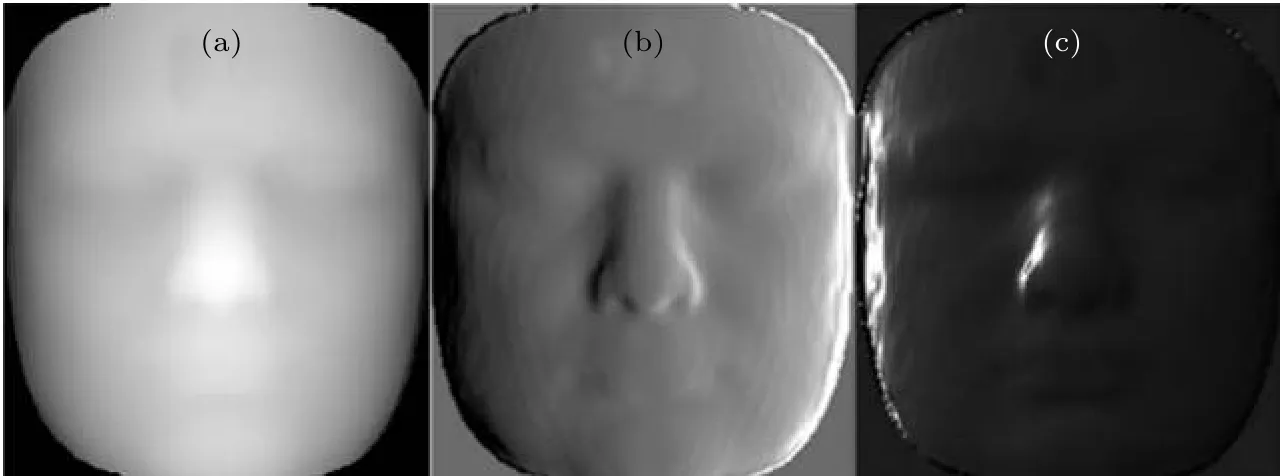
图2 (a) 仿真人脸深度信息; (b), (c) 通过渲染后的漫反射和镜面反射仿真图像Fig. 2. (a) Simulated face depth information ; (b), (c) simulated images with diffuse and specular reflections after rendering,respectively.

图3 基于二色反射模型的四幅模拟图像 (a), (b), (c), (d)分别代表(8)式混合后的光强分布 I 1T otal , I 2T otal , I 3T otal 和I4TotalFig. 3. Four simulated images based on dichromatic reflection model, (a), (b), (c) and (d) represent the intensity image I 1T otal , I 1Total ,I3T otal and I 4Total obtained from Eq. (8), respectively.

此时设定的真实分量混合系数矩阵为

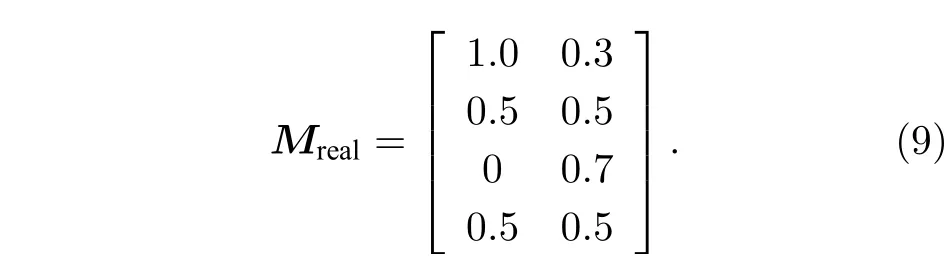
根据第3 节中提出的反射分离算法, 不断改变β利用(6)式获取不同的W矩阵来得到不同的分离结果, 利用(7)式计算每次分离后两个子分量间的互信息结果如图4 所示, 当β=0.545 rad 取得极小值时镜面反射与漫反射图像的相关性最小, 在该条件下求得的W矩阵可以得到最佳分离结果, 此时算法求取的混合系数矩阵M'如(10)式所示, 通过与(9)式真实混合系数做对比可发现, 本文提出的算法有效恢复了仿真图像的子分量混合系数, 成功提取出了漫反射分量与镜面反射分量,

在算法分离过程中得到的所有互信息值如图4所示, 其中图4(a), (b)分别是互信息在最小处β=0.545 rad 时所得到的漫反射分量与镜面反射分量的分离结果. 图4 中随着β增大到2.4 位置开始, 互信息值出现明显剧烈的起伏运动, 首先是由于该图的处理对象是仿真的镜面反射与漫反射分量随意组合的结果, 其两者之间较低的相关性导致纵坐标范围在0—0.17 之间, 会进一步突显抖动的剧烈程度. 其次, 在计算互信息(MI)(IDpiffuse,ISppecular)时, 由(7)式可知, 需要统计IDpiffuse和ISppecular图像中所占每一灰度级像素的个数, 随着β∈[0,π] 的改变, 将会得到具有不同程度相关的两幅图像, 若其中一副图像部分区域的像素值在原来的基础上减小1, 也会导致在统计灰度级的个数时, 数目发生明显迁移, 从而导致位于该灰度级像素的概率发生变化, 进而导致分布函数突变. 该现象在任意一段由β改变所导致图像灰度级所占像素个数发生明显迁移的过程中都可能存在, 仅仅与β改变时其每次增加的间隔大小有关系, 但是随着分离过程的进行, 所获得的子分量图像会逐渐接近最独立的状态, 互信息度的值总会呈现减小趋势, 从而达到最优的分离结果, 所以对β最小值的选取是没有影响的. 这里为了更加准确, 详尽的反映出β改变时对分离结果的影响, 设定β每次增加量只为0.001 去计算混合系数矩阵得到最终分离结果如图4 所示.

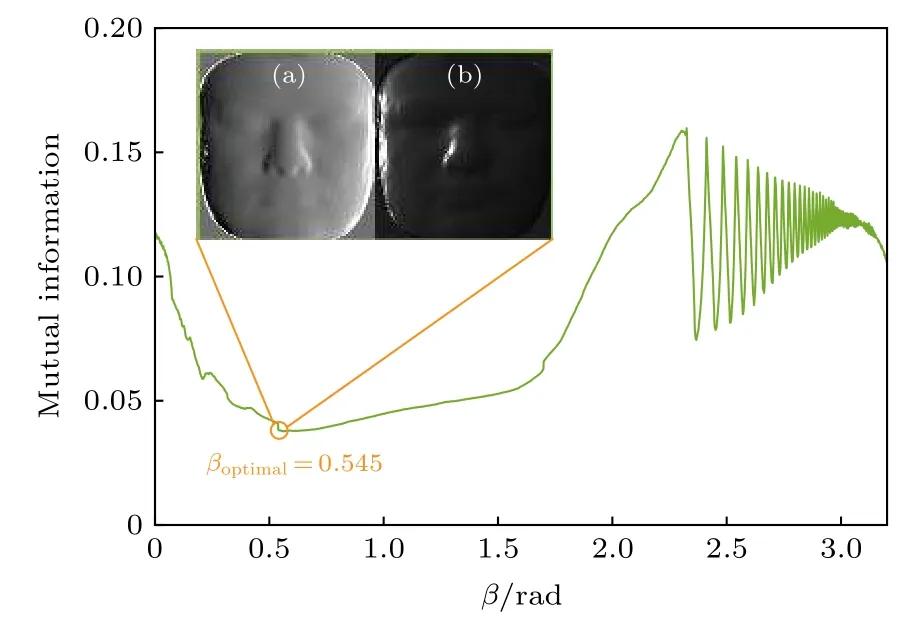
图4 互信息随β 变化情况及镜面反射和漫反射最终分离结果 (a) 分离的最优漫反射; (b) 分离的最优镜面反射Fig. 4. Mutual information variation and the finally separated diffuse and specular reflection: (a) The optimal separated diffuse reflection; (b) the optimal separated specular reflection.

为了验证算法的鲁棒性与稳定性, 保持分量混合系数矩阵第一列数值不变, 通过改变第二列中的四个系数进行精度分析, 结果如图5 所示. 曲线上的圆圈表示镜面反射分量混合系数所对应的设定值, 菱形表示通过算法获取到的镜面反射分量的系数值. 不同颜色的曲线变化是相对独立的, 代表4 个不同分量混合系数之间没有关联性. 同一颜色下每一组测试所对应的两个点的距离反映了处理效果的鲁棒性. 带有蓝色五角星的曲线表示每一组镜面反射分量设定值组成的向量与算法计算得到的系数组成向量之间的欧氏距离, 其值越小表示算法计算的数值越接近设定值. 对比其他几组数据来说, 第1 组和第7, 10 组的误差较大, 分析其原因主要是紫色线所对应的系数3 误差大导致的. 这是由于在计算时该系数在混合系数矩阵中所对应的漫反射分量系数值为0, 该部分漫反射分量不受约束, 而在利用基于ICA 架构的分离算法去求解时,由于算法不能无限逼近0 值, 漫反射分量无法实现绝对消除, 从而导致系数3 相对于其他三个系数来说误差大, 但是总体而言其误差不会超过0.1, 这意味着对最终分离结果影响不大.

图5 10 组仿真测试数据图 Coef1, Coef2, Coef3 和Coef4 是镜面反射分量混合系数的4 个设定值; Coef1-Ours, Coef2-Ours, Coef3-Ours 和Coef4-Ours 是算法得到的混合系数值; Eu-Dis 表示每组设定值组成的向量跟算法计算值组成的向量之间的欧氏距离Fig. 5. Plots of ten sets of simulation test data: Coef1, Coef2, Coef3 and Coef4 are four set values of the coefficients of the specular reflection components; Coef1-Ours, Coef2-Ours, Coef3-Ours and Coef4-Ours are the coefficients obtained by our algorithm; Eu-Dis represents the Euclidean distance between the vector composed of set values and the vector composed of the calculated values of our algorithm in each group.

考虑到生活中目标的多样性以及光场环境的复杂性, 利用Thorlab LPVISC100-MP2 线偏振片配合EOS77 D 佳能相机对一个非理想朗伯体陶瓷物体采集偏振子图像, 利用基于光场偏振特性的目标表面漫反射成分获取算法对真实场景下的目标进行镜面反射与漫反射分量分离, 结果如图6所示.

如图6(d)所示为偏振片在0°方向下获取的目标原始光强图片, 其中高光区域主要是由镜面反射造成的. 图6(e)和图6(f)分别是在互信息最小β=2.46 rad 时, 计算所得的真实场景下的镜面反射与漫反射分量. 图6(a), (b), (c)分别是图6(d), (e), (f)沿图示红虚线处的光强梯度分布, 表示每一像素位置处光强值的变化情况. 图6(a), (c)中300 像素位置附近存在尖峰, 光强梯度值产生突变, 这是镜面反射光的存在所导致的, 因此在去除镜面反射后的漫反射分量图6(b)中, 该位置不再存在梯度的突变. 图6(h)是图6(d), (e), (f)沿图示蓝实线位置获取的光强截面结果, 横坐标对应像素位置, 纵坐标表示光强值的大小, 由此可见, 总光强是镜面反射分量跟漫反射分量的线性叠加, 去除镜面反射后的漫反射分量光强分布符合物体表面形状的变化趋势.

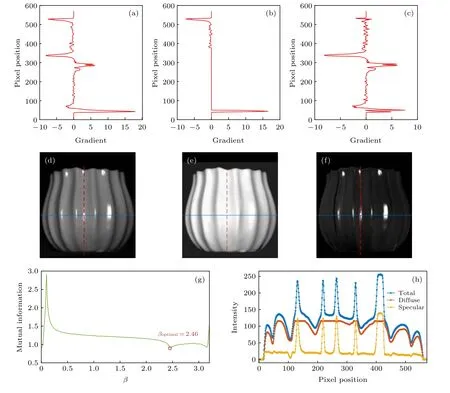
图6 陶瓷目标表面反射光强分布及分离结果 (a), (b)和(c)分别为图(d), (e)和(f)沿图示红虚线处的光强梯度分布; (d)是偏振片在0°方向下获取的目标原始光强图片; (e)和(f)分别是算法处理后最优的漫反射和镜面反射光强分布; (g)是算法处理过程中得到的互信息图; (h)是(d), (e), (f)沿图示蓝实线位置的光强截面结果Fig. 6. Intensity distribution and separation results on the surface of ceramic object: (a), (b) and (c) are the light intensity gradient distribution along the red dotted line shown in Fig. (d), (e) and (f), respectively; (d) is the original light intensity of the target obtained from the polarizer at the direction of 0°; (e) and (f) are the optimal light intensity distributions of diffuse and specular component after our algorithm, respectively; (g) is the mutual information plot obtained during algorithm processing; (h) is the results of light intensity cross section obtained along the blue solid line in Fig. (d), (e) and (f).

图7 其他目标反射成分分离结果 (a) 总光强分布; (b), (c) 分离后的漫反射分量和镜面反射分量光强分布; (d), (e), (f) 分别为(a), (b), (c)的光强空间显示结果Fig. 7. Reflection separation of three different objects: (a) Total light intensity distribution; (b), (c) light intensity distributions of separated diffuse and specular reflection, respectively; (d), (e), (f) spatial display of (a), (b) and (c) respectively.

为表征算法的普适性,本文还对其他表面纹理单一和表面纹理复杂物体的三种非朗伯体目标进行了实验,结果如图7 所示.图7(b)和图7(c)分别表示在各自对应互信息取得最小值时,所得的分离后最优的漫反射分量跟镜面反射分量,图7(e)和图7(f)是它们各光强分布的空间展示结果.由此可见,对于各类具有非理想朗伯体表面的物体,在考虑漫反射跟镜面反射所具有的部分偏振特性后,仍然能够有效地将叠加到一起的镜面反射分量跟漫反射分量进行分离,同时在镜面反射高光区域内成功地恢复出了物体表面的形状等细节信息,客观表明了基于光场偏振特性的目标表面漫反射分量获取技术的普适性.

5 结 论

针对三维重建、图像匹配及模式识别等技术中目标表面反射光复杂的问题,提出了基于光场偏振特性的目标表面漫反射分量获取技术.深入挖掘漫反射分量和镜面反射分量的部分偏振特性,利用二者的差异和互相独立的特点,建立线性约束模型;采用奇异值分解方法求解其最佳混合系数矩阵,从而实现了从复杂反射光场中对漫反射分量的精确获取和解译.仿真结果表明,该算法能够在无光源色度、方向及图像颜色信息等先验知识的前提下准确计算最佳混合系数矩阵,具有较好的分离效果稳定性与普适性.此外,实验结果证明了该算法不仅能够实现对镜面反射区域的精准获取,而且能够恢复出被镜面反射光所覆盖掉的符合物体表面形状变化趋势的漫反射光强值.该技术能够在图像分割、特征匹配以及模式识别等计算机视觉算法中,移除镜面反射强光的干扰,凸显物体表面的形状纹理等特征,克服复杂反射光场对目标结果的影响.同时由于该技术在进行反射分离时保留了漫反射分量所具有的偏振特性,提高了偏振探测方法的适用性.