铷原子系综自旋噪声谱实验研究*

杨煜林 白乐乐 张露露 何军2) 温馨3) 王军民2)†

1) (山西大学光电研究所, 量子光学与光量子器件国家重点实验室, 太原 030006)

2) (山西大学, 教育部-山西省-省部共建极端光学协同创新中心, 太原 030006)

3) (清华大学物理系, 北京 100084)

自旋噪声谱是一种测量自旋涨落的光谱技术, 由于无扰动的测量机制, 其光谱信号非常微弱. 本文基于含有一定压力的缓冲气体的天然丰度铷原子气室, 搭建了无外磁干扰的铷原子系综自旋噪声谱测量装置, 获得了微弱的铷原子系综自旋噪声谱信号, 实现了对铷原子系综自旋特性的测量与表征. 研究了探测光光强、频率失谐量、铷原子数密度等参数对自旋噪声谱信号的影响. 自旋噪声谱信号的积分与探测光光强的平方成正比, 光强会展宽自旋噪声谱的半高全宽. 自旋噪声谱信号的积分依赖于探测光的失谐量, 共振处呈现凹陷,这是由一定压力的缓冲气体的充入引起均匀展宽所导致. 自旋噪声信号的积分与原子数密度的1/2 次幂成正比. 本研究有助于铷原子自旋噪声谱技术应用于磁场的精密测量等方面, 也为高信噪比、小型化铷原子自旋噪声谱测量系统的研制提供了参考.

1 引 言

噪声的研究可以揭示系统的某些固有属性. 例如: 电流中的散粒噪声反映了载流子电荷的数目涨落; 电子系统的温度相关的热噪声(Johnson 噪声)反映了系统的电压涨落[1]. 自旋噪声(spin noise)在1946 年由Bloch 等[2]首次提出, 它表示核自旋系统中自旋向上和向下的随机涨落. 根据统计学原理, 对于包含N个磁性粒子且粒子之间相互作用可忽略的系统, 在热平衡态下其平均磁矩起伏正比于. 1981 年, Aleksandrov 和Zapasskii[3]实验上验证了碱金属原子的自旋噪声可以利用失谐激光以无扰动的方式通过法拉第旋转记录下来.1985 年, 原子核的自旋噪声首次由Sleator 等[4]测量得到. 2004 年, Crooker 等[5]基于法拉第旋转的光谱技术(自旋噪声谱, SNS), 对碱金属原子的自旋噪声进行了高信噪比的测量, 并预言了该光学技术在半导体自旋动力学及量子信息处理等方面的应用前景. 近年来, 随着探测方案的优化、数据采集及数据处理能力的提高, 自旋噪声谱技术成为非扰动光学探测的最佳手段之一[6−9]. 2007 年,Römer 等[10]首次利用实时傅里叶变换的高速采集卡来提高数据利用率, 将测量时间缩短两个数量级, 大大提高了信噪比. 与此同时, 相位控制技术及平衡零拍探测也是实现高信噪比及灵敏度的光学探测手段[11]. 此外, 偏振压缩光的使用可以突破散粒噪声的限制, 进一步提高了自旋噪声谱的信噪比[12,13]. 自旋噪声谱技术有助于进行一些基础物理量的测量, 包括同位素丰度比、朗德g因子、自旋相干寿命、超精细分裂、核自旋及核磁矩等的测量表征. 该技术除了研究传统的碱金属原子及半导体材料[14]之外, 还应用于纳米线[15]、量子点[16,17]等自旋系统.

本文搭建了铷原子系综自旋噪声谱测量装置,实验研究了探测光光强、频率失谐量、铷原子数密度等参数对自旋噪声谱信号的影响.

2 实验原理及装置

2.1 实验原理

自旋噪声谱是将自旋随机涨落映射在线偏振光偏振面的旋转上, 其基本物理机理是法拉第旋转的圆双折射检测. 自旋噪声谱技术的主要特点在于探测光光强小且大失谐于原子跃迁线, 对原子系综实现无扰动的光学探测. 采用Voigt 型[18]自旋噪声测量装置, 磁场B与探测光方向垂直. 实验原理示意图如图1, 失谐于铷原子D1 线的线偏振光作为探测光, 偏振面平行于磁场B. 探测光穿过由铷原子气室、λ/2 波片、沃拉斯顿(Wollaston)棱镜及差分探测器(DPD)构成的偏振干涉仪. 无磁场时设置λ/2 波片使差分探测器输出置零. 将铷原子气室的前内壁和后内壁看作两个分束器, 气室内光束路径长度为L, p偏振光在第一个分束器分解为空间上不分离等大的左旋圆偏光σ+和右旋圆偏光σ–本征矢量, 它们在铷原子气室内光束路径上干涉. 磁场B使铷原子基态Zeeman 态分裂, 由于存在分裂间距频率(νL=γ×B)相同的交流真空电磁场, 其随机涨落诱导铷原子基态相邻Zeeman态的磁偶极跃迁, 铷原子基态以拉莫尔频率被随机极化. 铷原子系综对左旋圆偏光σ+、右旋圆偏光σ–分量的吸收系数a±随之涨落. 根据Kramers–Kronig 关系,σ+、σ–光的折射率n±也不同[5]. 因此两正交分量的光程差L(n+-n−) 不为零, 在第二个分束器处矢量合成线偏光. 穿过铷原子气室的线偏光偏振面与入射光相比有频率为νL的微弱的随机旋转角θ. 探测器输出的光电流强度表征偏振光场的正交分量差值. 光电流信号送入快速傅里叶变换(FFT)分析仪, 从而得到自旋噪声谱[19,20].

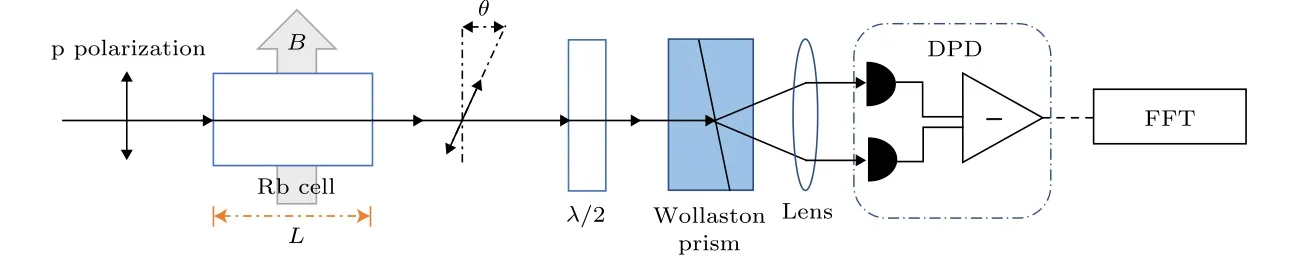
图1 铷原子系综自旋噪声谱的测量原理示意图Fig. 1. Schematic diagram of rubidium atomic ensemble spin noise spectroscopy measurement.

2.2 实验装置

实验装置如图2 所示, 795 nm 波长激光束由DBR 半导体激光器输出. 整形后激光主要分成三部分: 一部分较弱激光进入高精度波长计(Topica-Amstrong, High Finess WS-7)进行实时波长监测;另一部分激光通过天然丰度的铷原子气室, 通过铷原子D1 线饱和吸收谱实现激光频率与铷原子跃迁线的失谐量监测. 饱和吸收谱如图3 所示， 其中Fg为Rb原子基态总角动量量子数,Fe为Rb 原子激发态总角动量量子数; 激光主要部分经过高消光比的Glan Taylor 棱镜得到线偏振光束, 通过一定焦距的透镜使光斑聚焦, 穿过原子气室. 原子气室被放置在无磁保温材料的炉子内加热控温. 含原子气室的炉子放置于磁屏蔽筒中心. 输出激光信号经λ/2波片和Wollaston 棱镜(相对垂直偏振设置在45°)分束, 利用可变增益的差分光电探测器(PDB)(Thorabs PDB450)探测, 该探测方式对偏振面旋转信号敏感, 且能消除共模噪声[21]. 最后通过FFT动态分析仪(ZI Instrument MFLI)进行分析, 得到自旋噪声谱.

本实验具有良好的实验条件. 1) 激光器使用Photodigm 公司的795 nm 波长的DBR型半导体激光器, 在MHz分析频率段, 输出激光的强度噪声可达到散粒噪声水平, 光子数满足且由于探测光大失谐于原子跃迁线, 探测光的位相噪声不通过铷原子系综向光场的强度噪声转换.2) 采用天然丰度的圆柱型铷原子气室,φ= 20 mm,L= 30 mm, 内部充有10 Torr ( 1 Torr≈133.3 Pa )氖气(Ne)和20 Torr 氦气(He)作为缓冲气体. 无缓冲气体情况下, 由于铷原子和气室内壁碰撞导致

图2 铷原子系综自旋噪声测量的实验装置示意图. λ/2, 1/2 波片; APP, 整形棱镜对; ISO, 光隔离器; PBS, 偏振分光棱镜;NDF, 衰减片; M, 0°高反镜; λ/4, 1/4 波片; PD, 光电探测器; HF, 45°高反镜; DPD, 差分探测器Fig. 2. Schematic diagram of experimental setup for measuring rubidium atomic ensemble's spin noise spectroscopy. λ/2, half-wave plate; APP, anamorphic prism pairs; ISO, optical isolator;, PBS, polarization beam splitter cube; NDF, neutral density filter; M, 0°high-reflectivity mirror; λ/4, quarter-wave plate; PD, photodetector; HF, 45° high -reflectivity mirror; DPD, differential photodiode.

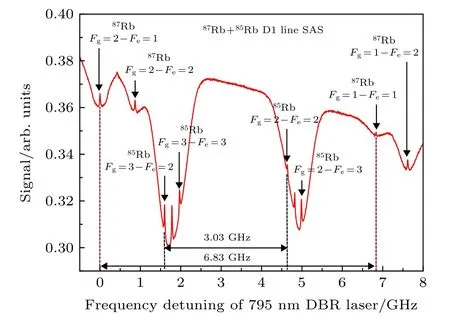
图3 铷原子D1 线饱和吸收光谱Fig. 3. Saturation absorption spectra of rubidium atomic D1 line.

其自旋弛豫时间缩短, 铷原子系综的自旋噪声谱线宽被非均匀展宽, 为高斯线型. 而Ne 和He 是惰性气体, 铷原子和其碰撞时, 基本上不改变铷原子的自旋态. 缓冲气体可以有效减少铷原子之间、铷原子和气室内壁的自旋破坏碰撞, 延长铷原子自旋的横向弛豫时间T2, 使自旋噪声谱本征半高全宽νh更窄,[14]. 因此, 选用有一定压力缓冲气体的铷原子气室作为介质, 此时铷原子系综的自旋噪声谱为均匀展宽的洛伦兹线型[22]. 原子气室内壁镀石蜡抗自旋弛豫膜也可以延长铷原子自旋的横向弛豫时间, 但不能耐受高温. 3) 放置铷原子气室的屏蔽筒由四层高磁导率坡莫合金构成, 原子气室处的剩磁小于2 nT. 由此屏蔽了地磁和实验室环境磁场, 避免磁场造成自旋噪声谱的漂移、展宽和干扰. 实验中磁场B为由低噪声恒流源驱动的磁屏蔽筒内的横向线圈产生. 采用交变电流加热技术及控温仪实现原子气室的加热控温, 为避开实验研究关心的MHz 频段, 加热电流频率设为600 kHz[23]. 4) Glan Taylor 棱镜消光比达20000∶1,探测光为高偏振度的线偏光. Wollaston棱镜也是高消光比的光学元件, 对微弱偏振面旋转很敏感.Thorlabs 公司 PDB450 型差分探测器在 MHz 的共模抑制比达到45 dB, 有效抑制测量系统的共模噪声.

3 实验结果及讨论

探测光频率相对于87Rb 原子52S1/2(F= 2) ↔52P1/2(F'= 1)超精细跃迁线失谐–10 GHz, 功率500 µW, 高斯直径约15 µm, 原子气室温度T=50 ℃, 所加横向磁场B= 3.448 G (1 G = 10–4T).图4 所示为典型自旋噪声谱, 黑线为实验测得的自旋噪声谱数据, 红色曲线为85Rb 自旋噪声谱的洛伦兹线型拟合曲线, 蓝色曲线为87Rb自旋噪声谱的洛伦兹线型拟合曲线. 峰值所对应的横坐标为铷原子在磁场中的拉莫尔进动频率νL, 分别约为1.596 和2.408 MHz. 洛伦兹曲线半高全宽 Δν分别约为82.15 和83.74 kHz. 本实验条件下, 由于横向磁场B在原子气室长度L上的不均匀和探测光的线宽、探测光频率起伏、光强起伏、光强横向在空间中不均匀[9]等因素的影响, Δν为铷原子自旋噪声谱本征半高全宽νh的上限值, 可知铷原子自旋的横向弛豫时间85T2＞3.87 μs,87T2＞3.80 μs . 铷原子的朗德因子gF取决于角动量量子数,

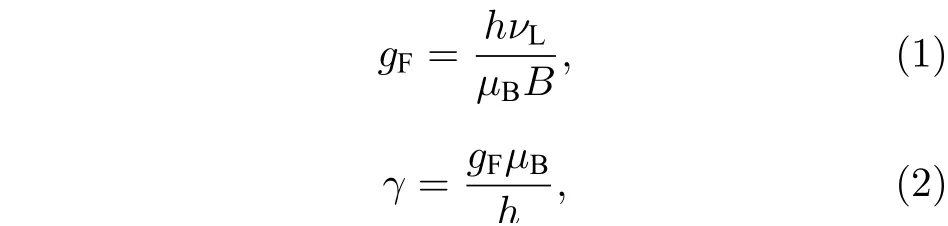
其中h为普朗克常数,µB为玻尔磁子,B为外加横向磁场, 经计算可得85Rb 与87Rb 对应的基态的朗德gF因 子 分 别 为85gF≈0.33516 和87gF≈0.50049 ,与 理 论 值85gF=1/3 和87gF=1/2 近 似 相 等, 同 时根据(2)式可以得到两种同位素对应的旋磁比分别为85γ ≈4.69098 Hz/nT ,87γ ≈7.00061 Hz/nT ,与理论值85γ ≈4.681 Hz/nT,87γ ≈7.010 Hz/nT 接近.

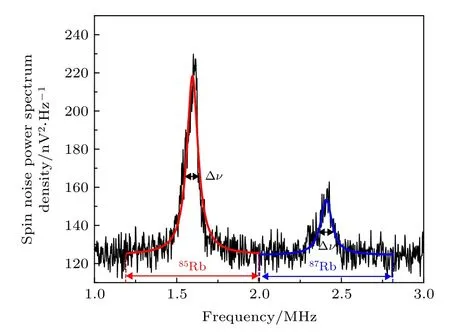
图4 典型的热平衡状态下铷原子自旋噪声谱Fig. 4. Spin noise spectra of rubidium atoms in a thermal equilibrium state.

3.1 自旋噪声谱与探测光光强的关系

图5(a)给出了自旋噪声谱功率谱密度随探测光功率的变化. 其他条件相同, 探测光功率由200 µW 增大至5.0 mW, 自旋噪声信号幅度随之增大, 信号峰的半高全宽也展宽. 根据铷原子自旋噪声谱的本征线宽只与铷原子自旋的横向弛豫时间有关, 可知探测光光强对自旋噪声谱的展宽应被充分消除才能得到本征线宽, 即测得铷原子自旋横向弛豫时间的必要条件之一是足够小的探测光光强.

分别对85Rb 与87Rb 原子的自旋噪声谱进行洛伦兹线型拟合, 积分得到其面积, 可以得到自旋噪声谱的信号幅度与探测光光强的关系, 如图5(b)所示. 差分探测输出的偏振面旋转信号F正比于光强I, 而自旋噪声峰信号幅度S是对偏振面旋转角信号进行FFT 变换再取模平方得到的, 因此积分的自旋噪声谱信号大小与光强I之间的关系为S ∝F2∝I2, 设系数为κ, 即S=κ×I2.κ与原子数密度、探测光的频率失谐量、横向磁场等参数相关. 拟合实验数据得到本实验条件下κ85Rb=0.71 ,κ87Rb=0.20.

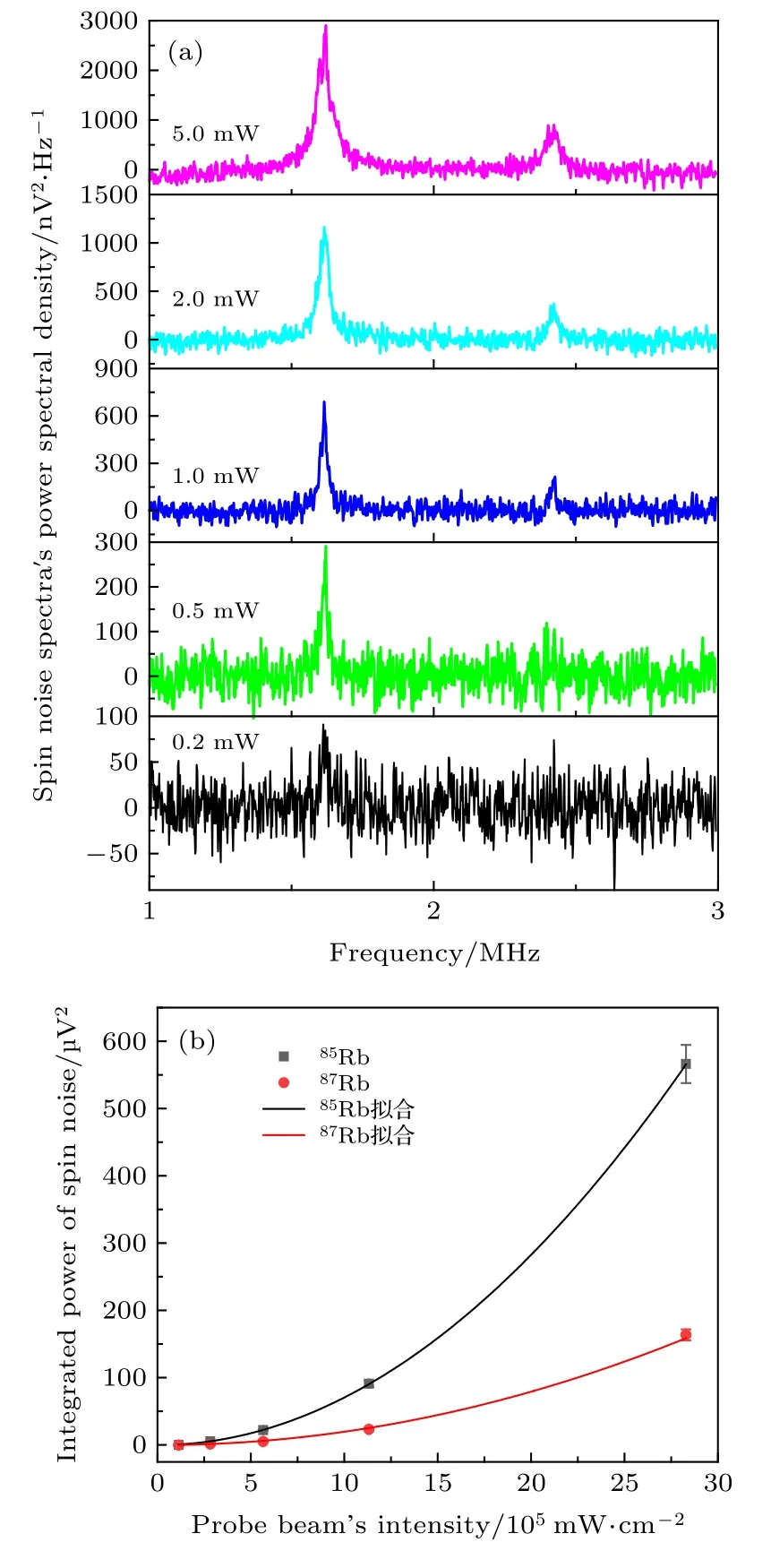
图5 (a) 不同探测光光强下的铷原子自旋噪声谱; (b)自旋噪声谱信号幅度与探测光光强的关系, S=κ×I2 拟合数据Fig. 5. (a) Rubidium spin noise spectra at different probe optical instensity; (b) relationship between spin noise spectrum signal amplitude and probe optical intensity, with the data fitted by S=κ×I2 .

3.2 自旋噪声谱信号与探测光频率失谐的关系

探测光光强约17.0 × 105mW/cm2, 横向磁场B= 0.345 G, 原子气室温度T= 50 ℃. 改变探测光频率, 图6(a)是同一气室的铷原子D1 线透射谱, 黑色方块为对应探测光频率处的透射率, 洛伦兹拟合得到红色曲线的半高全宽 Δνt为6.9 GHz.与图3 对比,85Rb 和87Rb 原子不同基态、激发态精细结构的谱线被覆盖, 主要展宽原因是探测光的强度展宽. 弱探测光时测透射谱得到的碰撞展宽约为1 GHz. 缓冲气体压强增大透射谱会进一步展宽. 透射信号谷底中心频率标为∆=0 . （注： 除本小结研究自旋噪声谱与探测光频率的关系外, 其余研究内容保持探测光频率相对于87Rb 原子52S1/2(F= 2) ↔ 52P1/2(F'= 1)超精细跃迁线中心频率失谐–10 GHz）.

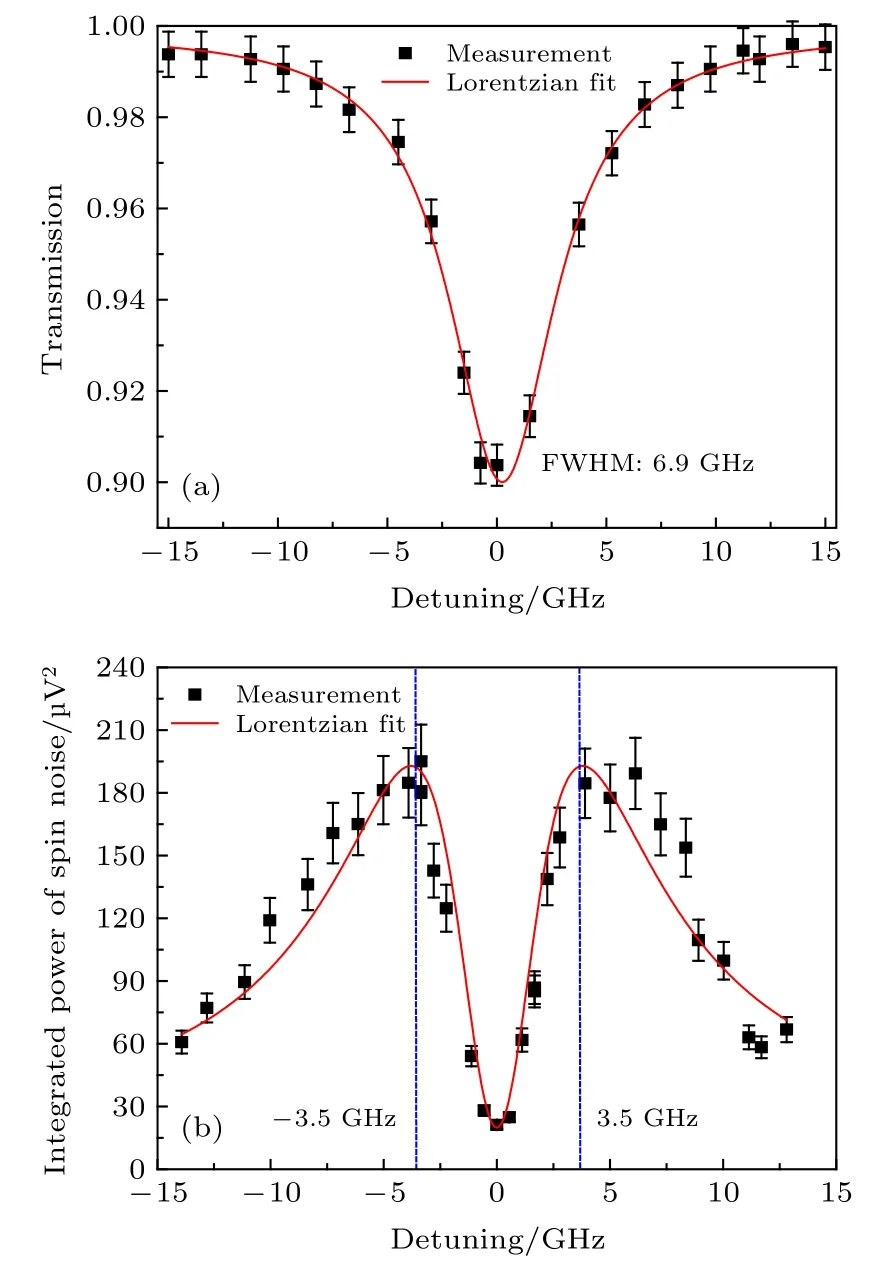
图6 (a) 铷原子D1 线的透射谱; (b)积分后的85Rb 自旋噪声信号随探测光频率变化. 黑色方块为实验数据, 根据(3)式拟合得到红色曲线Fig. 6. (a) Transmission spectra of rubidium atomic D1 line; (b) 85Rb spin noise signal intensity (integrated) varies with probe light frequency in a naturally isotopic abundant rubidium atomic ensemble containing 10 Torr neon gas and 20 Torr helium gas. The black squares are experimental data and the red curve is fitted by Eq. (3), respectively.

探测光频率依次固定于从∆=-15 GHz 附近到∆=+15 GHz 附 近 的 若 干 频 率 失 谐 值 处,积 分的85Rb 原子自旋噪声信号的变化如图6(b), 呈现M 型. 探 测 光 失 谐 在 3.5 GHz<|∆|<15 GHz 时,积分的自旋噪声信号正比于∆−1. 表明失谐的探测光对铷原子基态自旋随机涨落导致的色散率变化敏感, 与前人的研究结果一致[5]. 对于|∆|<3.5 GHz 时, 积分的自旋噪声信号减小, 在共振处自旋噪声信号最小. 这也是由于缓冲气体对铷原子的碰撞, 使自旋噪声谱信号关于探测光频率均匀展宽. 图6(a)透射谱的洛伦兹线宽和图6(b)的自旋噪声凹陷的全宽频率间隔接近. 图6(b)数据拟合公式为[6,8]

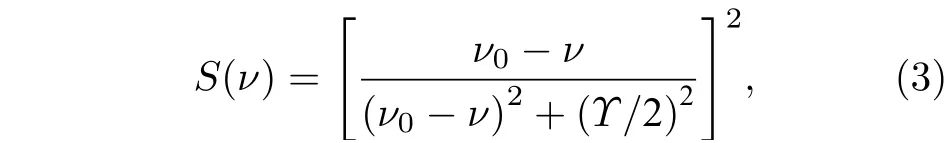
其中S是积分后的自旋噪声信号,ν为探测光频率,ν0为中心频率,Υ为透射谱的线宽.

3.3 自旋噪声谱信号与原子数密度的关系

图7 为85Rb 的自旋噪声谱信号与原子数密度n的关系. 探测光光强约1.7 × 105mW/cm2,横向磁场B= 3.448 G, 探测光频率相对于87Rb 52S1/2(F= 2) ↔ 52P1/2(F'= 1)失谐–10 GHz. 控制铷原子气室温度分别在25, 35, 45, 55 和65 ℃,n相应地增加[24],

其中p是压强,T是开尔文温度,n是85Rb 原子数密度,kB是玻尔兹曼常数.

图7(a)显示, 随着铷原子数密度的增加, 自旋噪声谱信号幅度变大, 自旋噪声谱的半高全宽随温度升高而展宽. 根据(4)式, 铷原子气室温度升高,铷原子数密度增大, 贡献的自旋噪声也增大. 铷原子间、铷原子和气室内壁的自旋破坏碰撞也更剧烈, 导致铷原子自旋的横向弛豫时间缩短, 即原子数密度越大自旋噪声谱的本征线宽越宽.

横向磁场在铷原子气室内的不均匀导致探测光路径上不同空间位置的铷原子拉莫尔进动频率不一致, 使得谱线展宽. 实验测得在铷原子气室长度内横向磁场的不均匀性为 ± 0.22%, 最大值Bmax=3.455G,最小值Bmin=3.440G.那么自旋噪声谱中心至少展宽了ν∆=γ×(Bmax-Bmin)= 7.1 kHz .

自旋噪声谱信号积分后与原子数密度的关系如图7(b)所示,黑色方块为自旋噪声谱信号的积分.热平衡条件下数密度为n的铷原子的涨落为,对自旋噪声的贡献为S=ζn1/2.系数ζ与原子数密度、探测光光强、失谐量、横向磁场等参数相关.对数据拟合得到红色曲线,ζ=1.1.

图7 (a)不同温度(25−65℃)下85Rb 原子的自旋噪声谱;(b)不同原子数密度下的自旋噪声信号Fig.7.(a)Spin noise spectrum of 85Rb at some different temperatures(25−65℃);(b)the spin noise signal am plitude versus atomic number densities.

4 结 论

本实验基于充有10 Torr氖气和20 Torr氦气作为缓冲气体的天然丰度铷原子气室作为介质,搭建了磁屏蔽环境中的铷原子自旋噪声谱实验系统,得到了典型的铷原子自旋噪声谱信号.研究了自旋噪声谱对探测光光强、频率和原子数密度等参数的依赖关系.积分的自旋噪声谱信号与探测光光强的关系为S∝I2.铷原子气室的透射谱半高全宽被均匀展宽,Δνt=6.9GHz.透射谱中心对应的探测光频率标为∆=0.积分的自旋噪声谱信号与探测光频率失谐量的关系为:探测光频率失谐量从大失谐到透射谱的半高全宽过程中,积分的自旋噪声信号反比于失谐量,即|∆|＞Δνt/2时S∝∆−1;探测光频率失谐量在透射谱的半高全宽范围内|∆|<Δνt/2时,积分的自旋噪声信号呈现一个凹陷,这是缓冲气体和铷原子的碰撞导致的.积分的自旋噪声谱信号正比于原子数密度的平方根,即.温度升高铷原子自旋的横向弛豫时间变短.在非扰动的探测条件下的自旋噪声谱半高全宽接近本征线宽,包括探测光远失谐、弱光强、横向磁场均匀等.除此之外,缓冲气体的分压比、光场噪声等也会对原子系综自旋噪声谱产生影响. 本实验为高信噪比、小型化、鲁棒的实用型碱金属原子自旋噪声谱仪的研究积累了经验.下一步将利用偏振压缩光进一步提高自旋噪声谱的精度,实现突破标准量子极限的测量.

感谢日本国立电气通信大学(UEC)硕士研究生Koh Minorikawa(御法川·航)在本实验早期所做的贡献.