基于改进飞蛾扑火算法的机场航班时刻衔接优化

严 宇，熊 静，张文成，刘 超 YAN Yu, XIONG Jing, ZHANG Wencheng, LIU Chao

（上海工程技术大学 航空运输学院，上海201620）

(Air Transport College, Shanghai University of Engineering Science, Shanghai 201620, China)

0 引 言

目前我国航空旅客周转量快速增加，由2014 年的6 334.19 亿人次增长到2019 年的11 705.10 亿人次。虽然现在的航空网络非常发达，但也不是任意两个机场之间都可以直航，但是可以选择合适的中转机场到达自己的目的地。旅客不希望中转候机时间太长，这样就要求中转机场对到达航班和接续航班的时刻能够很好的衔接。由于枢纽机场日航班起降量大，要讨论的是整个枢纽机场各个航向上的衔接，计算数据量庞大，必须使用优化算法对目前航班时刻表进行优化。

在航班时刻表优化问题上，目前使用的算法有：粒子群算法、遗传算法、模拟退火算法、蚁群算法等。齐莉[1]以航班调整量最小为目标考虑了航班的衔接水平，并用基于小世界效应的快速搜索算法求解。徐晨等[2]建立了国际航班中转效率最大为目标的航班时刻优化模型，提出针对不同航班特性的时隙优化方法，最后通过遗传算法优化禄口机场时刻表。随着科学的进步，不断有新的仿生算法出现。澳大利亚的Mirjalili[3]提出了一种模仿夜间飞蛾横向定位导航方式的新颖启发式算法——飞蛾扑火算法（MFO算法），且该算法全局搜索能力和局部收敛速度均优于以上优化算法。目前，关于该算法的研究也刚刚开始[4-5]，其应用研究有：把飞蛾扑火算法应用于水资源的优化配置问题[6]、作业间车辆的调度问题[7-8]等，用于机场时刻表的优化研究还很少。本文将以枢纽机场各个中转航班对的平均衔接时间最小为目标，利用改进飞蛾扑火算法（MFO算法） 给出新的航班时刻表。

1 最小机场衔接时间的优化模型

首先，在航班飞行方向上用绕航系数筛选合适的城市对；然后在机场运行约束下，针对城市对的衔接航班进行最小衔接时刻优化。

1.1 相关概念

绕航系数影响枢纽机场对旅客的吸引力[9]。设Dik为始发机场i与枢纽机场k的距离，Akj是枢纽机场k与目的地机场j的距离，Dij是始发机场i与目的地机场j的距离，定义绕航系数Rij如下：

航班时隙、计划过站时间、机场时刻容量需要满足国家的相关要求。

1.2 航班时刻表优化问题解析与模型构建

1.2.1 确定满足绕航条件的航班对

设出发城市集合为X=｛i|i=1,2,3,…,n｝；抵达城市集合为Y=｛j|j=1,2,3,…,n｝；枢纽机场为k；由式（1） 绕航系数的定义可知，一般情况下Dik+Akj≥Dij，即Rij≥1。根据文献[11]，绕航系数Rij的范围选定可认为小于等于1.4 时，转机有效；大于1.4时，为无效转机。由此定义转机决策系数uij：

1.2.2 目标函数

考虑所有可中转城市对的所有航班的平均衔接时间，使得它们的和最小。目标函数为：

其中：是i市到j市的中转等候时长；kij表示一条i市到j市的转机线路。对航班时刻表的优化，符合绕航系数的城市对是航班时刻优化的前提，机场时刻容量、航班最小过站时间相互影响，又是航班时刻优化的约束，目的是使枢纽机场平均旅客的衔接时间最小。

1.2.3 约束条件

在本研究中，根据已有航班时刻表，认为航空公司已安排合适的机组和机型。因此，认为航班时刻表优化问题的限制条件为机场运行时刻限制、飞行器最小过站时间限制和航班调整时间限制。

定义以下参数：ij城市对航班中，i城市到枢纽机场的航班抵达时刻（k1代表某航班）；ij城市对航班中，枢纽机场到j城市的航班出发时刻（k2代表某航班）；枢纽机场的平均旅客衔接时间Zk；i市到j市的转机线路总数Xij。航班时刻表应满足约束如表1 所示。

表1 模型约束条件

2 改进飞蛾扑火算法

2.1 传统飞蛾扑火算法

2015 年格里菲斯大学学者Mirjalili 根据飞蛾围绕火焰做对数螺旋曲线轨迹的行为提出了飞蛾扑火算法（Moth-flame optimization algorithm，MFO）。设矩阵M为飞蛾的集合，即当前的搜索位置，矩阵OM为飞蛾的适应度值；矩阵F为烛火的集合，即当前的搜索的最优解位置，矩阵OF为烛火的适应度值。问题的变量为空间中飞蛾的位置，通过改变飞蛾的位置向量，逐步得到最优的烛火位置。

记：

式中：n指飞蛾的数量，d指变量的维数。

MFO算法是一个近似优化问题全局最优的三元组：

I是一个生成飞蛾随机种群和相应适应度值的函数。I的模型如下：

算法中的主函数P，它负责在搜索空间中的移动飞蛾。这个函数接收M的矩阵，并最终返回其更新后的矩阵。函数P可以表示为：

T函数是终止条件判断函数。若终止条件满足，T函数返回true，如果终止条件不满足，返回false。函数T可以表示为：

记Mi为第i只飞蛾的位置，Fj为第j个火焰的位置，b为对数螺旋函数的一个常数；t为［-1,1 ］之间的随机数。飞蛾的螺旋模拟飞行公式如下：

飞蛾通过此迭代公式不断更新自己的位置，最后求得火焰的位置。由于飞蛾的路径是逐步接近火焰的，所以其迭代过程很容易陷入局部最优解。因此，得到新的火焰后，对所有火焰的适应值排序，通过式（13） 得到火焰数量的自适应变化公式。其中，N为烛火数目的最大值，l为当前迭代次数，T为最大迭代次数。

2.2 改进的飞蛾扑火算法

传统MFO算法中飞蛾位置的更新机制是使飞蛾飞向烛火，但易使飞蛾错过全局最优，有一定的不足。本文引进自适应权重方法，当飞蛾在靠近最优解时，自适应权重的值减小，可以提高算法后期的探测能力[10]。自适应权重ω 的具体计算公式如下：

由此得到更新的飞蛾位置：

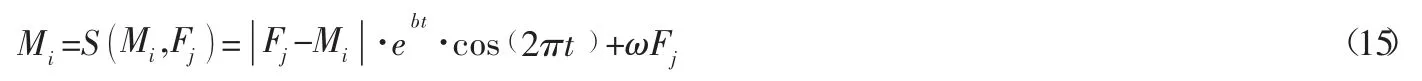
随着迭代的进行，ω 的值由1 到0 逐步减少，迭代步长变短，避免了飞蛾错过最优解。通过测试函数检验，改进后的MFO算法具有较好的收敛精度和全局寻优能力，寻优效果优于传统的MFO算法。

改进MFO算法流程结构如图1 所示。

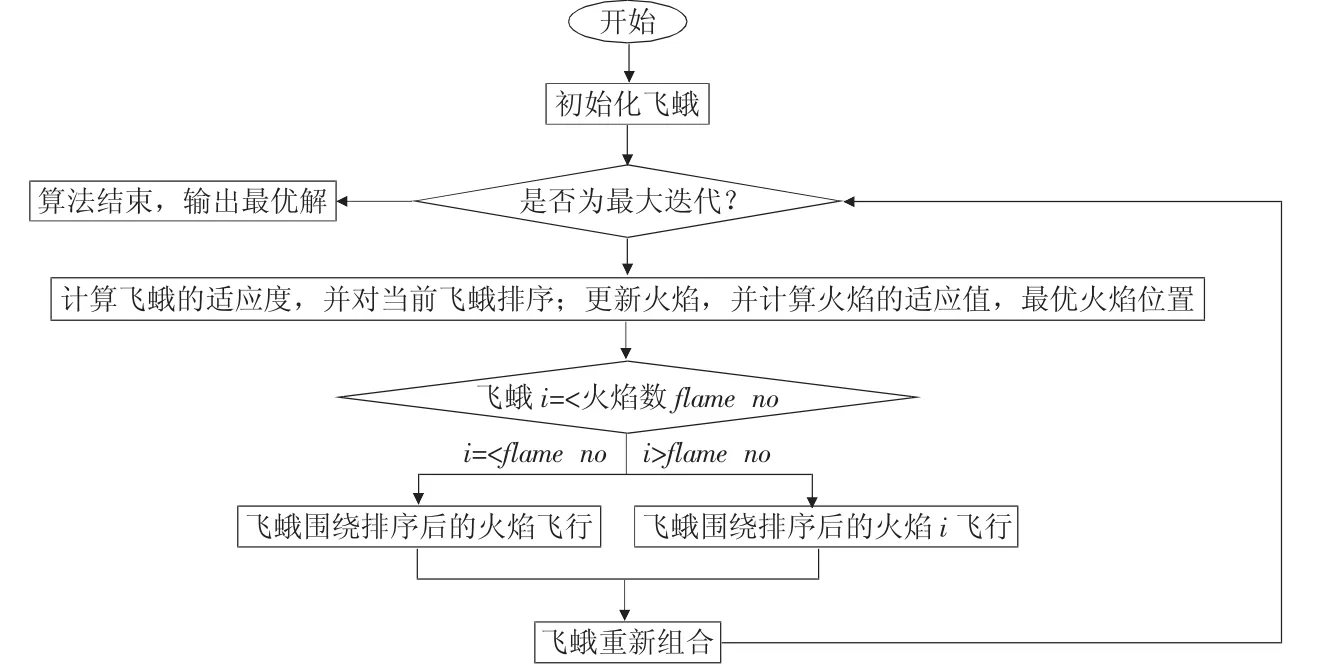
图1 改进MFO 算法流程图

3 运算实例分析

西安咸阳机场是我国西部重要的航空枢纽机场。本文以西安咸阳机场为中转枢纽机场，利用改进飞蛾扑火算法，以优化衔接时间最小为目标进行时刻优化。根据2019 年7 月8 日西安咸阳机场的国内航班时刻表，通过Matlab R2018a 仿真，得到以下优化结果。

（1） 航班平均衔接时间

使用传统MFO算法与改进MFO算法航班优化后平均衔接时间与迭代次数的关系如图2所示。

由图2，传统MFO算法得到的平均衔接时间为1.45 小时，改进的MFO算法得到的平均衔接时间为1.26 小时，说明改进的MFO算法寻优能力优于传统MFO算法。

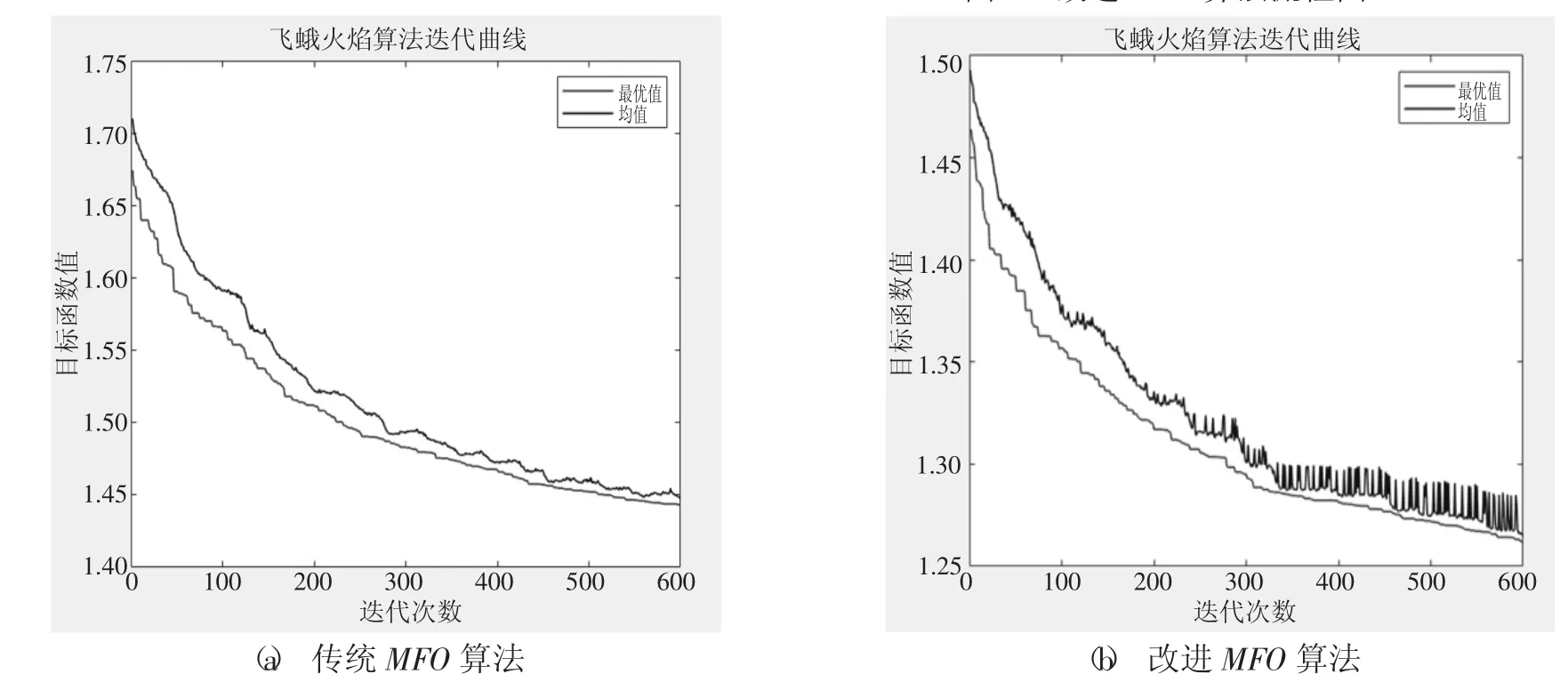
图2 西安机场的航班时刻表优化的目标函数值计算

（2） 优化后中转信息

输出优化后的西安机场航班时刻表符合要求的中转航班对共有1 688 对，数据较大，此处不一一列出。仅举一例，延安机场一天有2 班至西安的航班，按改进MFO算法优化后的转机衔接航班共有21 个，如表2 所示。

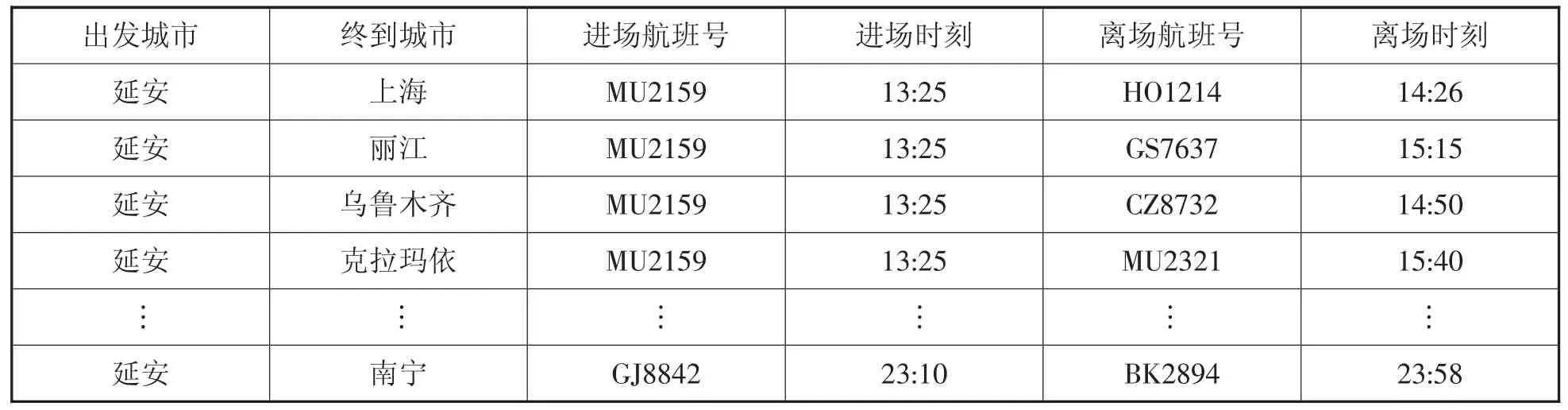
表2 优化后的西安机场时刻表延安与其他城市的中转航班对

（3） 航班调整时间量

原始航班时刻表经改进MFO算法优化后航班需调整时间如表3 所示（部分）：

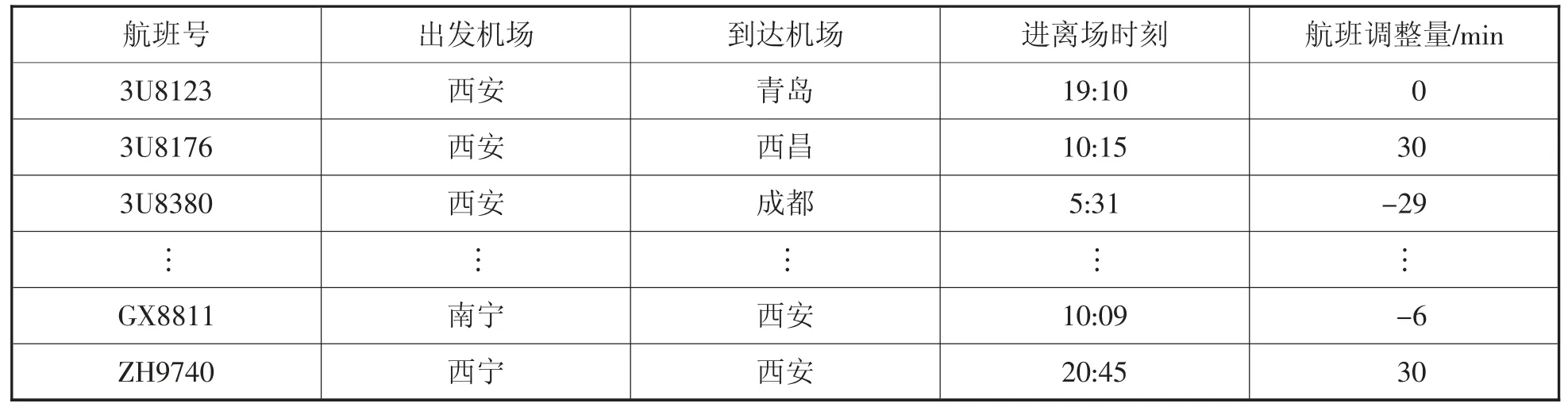
表3 优化后西安机场时刻表的调整时间

（4） 调整量分布

原始航班时刻表经改进MFO算法优化后航班调整时间分布如图3 所示。

在西安机场起降的812 个航班中，有618 个航班的调整量为26～30min。可见为了满足转机条件，航班需要进行较大规模的调整，若机场航班时刻表的优化应用则需要多方面协调。

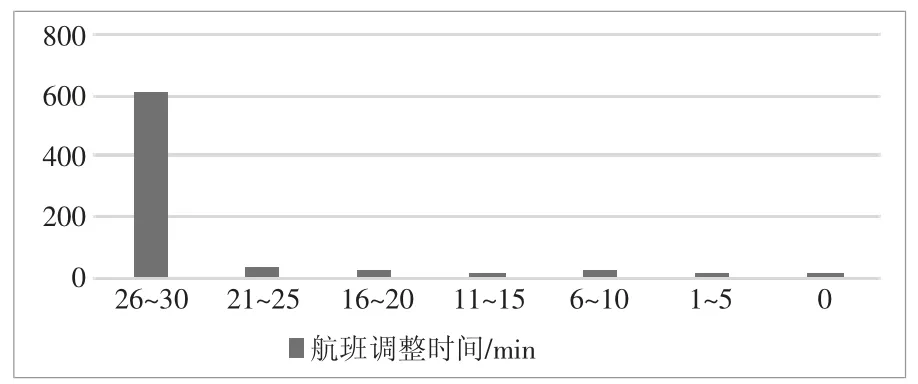
图3 西安机场时刻表优化后航班调整时间分布

4 总 结

航班时刻表中转时刻优化对我国建设区域枢纽机场及支线航班网络建设有较大的实用价值。本文首先筛选适合中转的航班对，建立优化模型，通过仿真实验，介绍飞蛾扑火算法的原理，并说明使用改进飞蛾扑火算法优化航班中转衔接时间优于传统飞蛾扑火算法，改进后的航班提高了枢纽机场的整体衔接水平。本文算法还可以给出各机场在中转机场具体的各方向中转时刻表，适用性广。

下一步研究，航班时刻模型可以涉及机场资源、航路资源等，在CDM 系统上对航班时刻中转优化。