基于超越对数成本函数的航空公司延误成本测算

朱 江，黄建伟，亓洋洋，王乐乐 ZHU Jiang, HUANG Jianwei, QI Yangyang, WANG Lele

（上海工程技术大学，上海201620）

(Shanghai University of Engineering Science, Shanghai 201620, China)

0 引 言

随着我国社会经济的快速发展，我国民航运输业发展迅速，快速增长的市场需求同民航有限的资源之间的矛盾导致我国航班延误现象日益严重。如图1 所示，从2011 年至2015 年，国内主要航空公司航班正常率不断走低，2015 年正常率仅为68.90%，在国际上处于落后水平。经过不懈的治理，近年来航班延误率有所减少。2016 回升至76.54%，2017 年又跌至71.25%，2018 年正常率增至79.95%，但仍未达到民航管理当局设定的高于80.00%的目标，航班延误问题仍然严峻。

图1 国内主要航空公司航班正常率

航班延误将导致航空公司运营成本的增加，包括航空器消耗更多的燃油，飞机等高价值设备资产的利用率降低，机组等人员工资支出增加等。都业富、田振才（2004）[1]通过研究测算1992 年至2002 年航班延误的成本，并预测了2004 年至2020 年航班延误成本，指出我国航班延误成本呈逐年上升的趋势，值得引起重视。但是基于20 年前数据对未来十余年的航班延误成本所作的长期预测，通常很难确保预测精度。因此，对航班延误问题建立数学模型，通过定性和定量分析较为准确地估算航班延误对航空公司带来的成本负担，将有利于航空公司发现经营管理中的薄弱点，并针对出现的问题采取相应改善措施。为了测算航班延误给航空公司所带来的损失，本文将构建航空公司航班延误Trans-log 成本函数模型，并将包含有航班延误架次的航空公司经营过程中的众多解释变量纳入，研究航空公司航班延误对航空公司运营成本的影响，并针对研究结果提出相应的对策建议。

1 文献综述

航班延误引起的航空公司成本估算方法通常分为两类。第一种是从航班运行的角度将航班运行的各个环节进行分类，分别计算各环节中航班延误引起的损失，最后将其汇总估算出航班延误总损失。李雄、刘光才等（2007）[2]通过将航班延误损失划分为航空公司损失、旅客经济损失以及非经济性的隐性损失，结合各环节各类损失计算公式，测算了2004 年及2005 年航班延误的经济损失。赵文智、刘博（2011）[3]通过将航班延误成本划分为常值费用、油费和时费三类，构建航班延误成本模型，对B737-800 与A320-200 两种常见机型进行延误成本测算，指出在长时间延误下，旅客的食宿费占比会随着延误程度逐步上升。

第二种是从宏观的角度构建相关模型，将航班延误或其它延误相关变量作为模型的解释变量，通过模型的拟合结果以及航班延误相关变量在模型中对应系数的二者关系，从而估算航班延误对航空公司运营成本的影响。2010 年，美国NEXTOR 研究了2007 年航班延误对美国航空公司的影响，运用了超越对数成本函数测算了航班延误造成的航空公司损失[4]。武勇彦、鱼海洋（2017）[5]采用对数函数建立了航班航程与航速之间的关系，测算了2005 年中国航班时间延误损失。冯敏、李鹤等（2007）[6]通过构建柯布—道格拉斯成本函数模型进行了估计，综合考虑了各类影响，指出此模型适用于大规模、长时间的延误成本测算。陈俣秀、于剑（2016）[7]通过将航班延误时间作为模型的解释变量之一，构建航空公司的成本函数模型，测算了2013 年国内航班延误的航班计划时刻延误损失与航班计划缓冲时间损失。

以上第一种方法不适用于长时间，全行业大规模的航空公司延误成本测算，第二种测算方法大多只考虑到延误时间这一解释变量，而本文提出的延误架次对比延误时间有着更好的数据可获得性和验证性。因此，本文针对如上情况将航班延误架次作为解释变量，且以近年航空业的实际数据作为基础，构建航空公司Trans-log 成本函数模型。该模型从宏观的角度整体测算航班延误对航空公司成本的影响，为航班延误的治理打下理论基础。

2 模型构建

2.1 影响因素选择

企业的成本函数被定义为：在给定的投入要素价格Pit下，生产一定数量的产品Qit（i表示特定的航空公司，t表示时间），其成本：Y=f（Qit,Sit,Pit）。这表明可以通过构建航空公司成本函数模型来反映和研究航空公司的生产全过程，其中Qit表示航空公司的产出，本文选择收入吨公里（RTM，Revenue-Ton-Miles） 来表示航空公司产出；Sit表示投入资本；Pit表示投入要素价格，航空公司的投入要素价格主要有三种，即燃油价格、材料价格及劳动力价格。

航空公司的成本也取决于航空公司产出的性质、质量及数量，因此在构建成本函数时需要考虑网络经济对航空公司的影响[8]。网络经济性包含密度经济性和范围经济性，密度经济性指航空运输在保持平均航程、平均载运率及通航城市数量的基础上，由于航空公司客货运输量的增加导致的单位运输成本的下降；范围经济性指航空公司增加通航点扩大通航范围时获得更广的辐射范围，在维持航班平均航程、平均载运率和平均通航点运输量不变的情况下，航空公司运输的单位成本的下降。因此需要在成本函数模型中考虑航空网络运营特点Nit，即Y=f（Qit,Sit,Pit,Nit）。Nit主要包含该航空公司的平均航程、平均载运率和通航城市数量。

航班延误是航空公司生产活动中难以杜绝的扰动因素，天气情况、空域管制、航空公司以及旅客等造成航班延误的原因，航班延误的发生则会增加航空公司的运营成本。因此，航空公司成本函数又可以扩充为Y=f（Qit,Sit,Pit,Nit,Dit），其中Dit表示航班延误情况，本文模型中的延误情况主要指航班延误数量，模型相关解释变量如表1 所示：

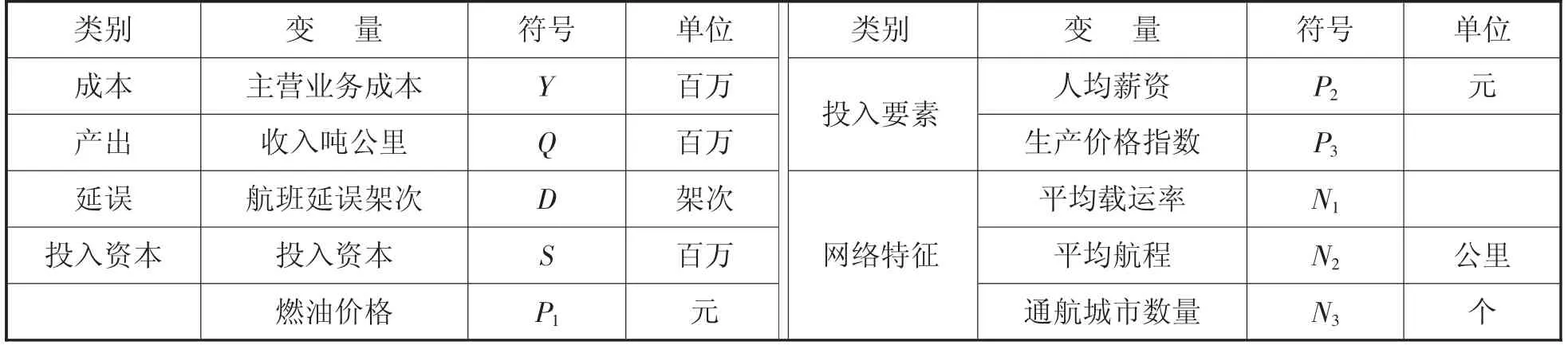
表1 解释变量

2.2 模型构建

超越对数成本函数（Trans-log Cost Function, TCF）[9]实际上是Cobb-Douglas 成本函数的扩展，与Cobb-Douglas 成本函数相比，Trans-log 成本函数不以固定弹性为假设前提条件，其参数更容易通过标准统计方法进行估计。

模型使用的数据类型为面板数据，因此模型中包括了时间虚拟变量Tm及横截面虚拟变量Ln，目的是为了表示随着时间而发展的技术变化及某一航空公司对成本的特有影响；Pi（i=1,2,3）表示航空公司第i种投入要素的价格，分别是燃油价格、人均薪酬及材料价格[10]；Ni（i=1,2,3）表示航空公司第i种网络运营特征，分别是平均载运率、平均航程及通航城市数量；D表示航班延误架次，为了使得平航班延误架次能够取到0，取其状态值。

本文基于超越对数成本函数（Trans-log Cost Function, TCF） 构建航空公司成本函数模型，如式（1） 所示。

Trans-log 函数需要满足投入要素价格的线性齐次性[11]，因此，本文所建立的公式（1） 需要满足以下的条件：

Shephard's lemma 指出投入要素的成本分摊份额方程可以用成本函数求出投入要素价格的偏导数得出[12-13]，以所建立的模型求投入要素价格Pi（燃油价格P1、人均薪资P2、生产价格指数P3） 的偏导数，结果如式（3） 所示：

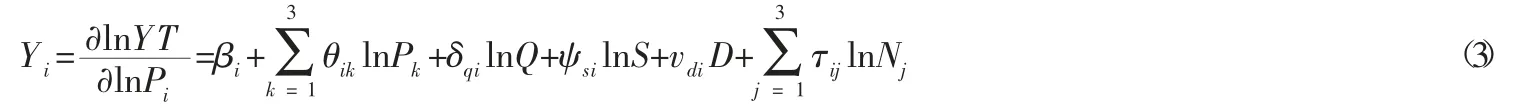
一般对成本函数（1） 与成本份额等式（3） 联立求解以增加求解效率，联立求解采用似无关回归（Seemingly Unrelated Regression, SUR）[14]方法进行估计。并且为了克服异方差奇异矩阵问题，一般在使用SUR 方法求解之前去掉一个成本份额等式[15]。

3 数据及其描述性分析

本文采用2014 年至2018 年国内主要的4 家航空公司的面板数据（中国东方航空公司、中国国际航空公司、中国南方航空公司、海南航空公司）。2011 年至2018 年4 家主要航空公司运输总周转量均达到国内全部航空公司总周转量的85%以上。

数据主要来源于各大航空公司年报、官方网站、中国统计局以及中国民航局年度报告。其中主营业务成本、收入吨公里、人均薪酬、平均航程、通航城市数量及平均载运率均来源于航空公司年报。平均燃油价格鉴于数据可获得性，因此采用了布伦特原油价格作为参考。航空公司投入资本主要包括飞机及发动机、地面房屋建筑及高价周转件的价值。由于航空公司投入要素价格中的材料价格获取有难度，因此本文采用了扣除通货膨胀因素的生产价格指数（PPI） 表示材料价格的变化。国内航班延误架次可通过民航局年度报告与航空公司年报数据计算获取，相关数据描述性统计如表2 所示。

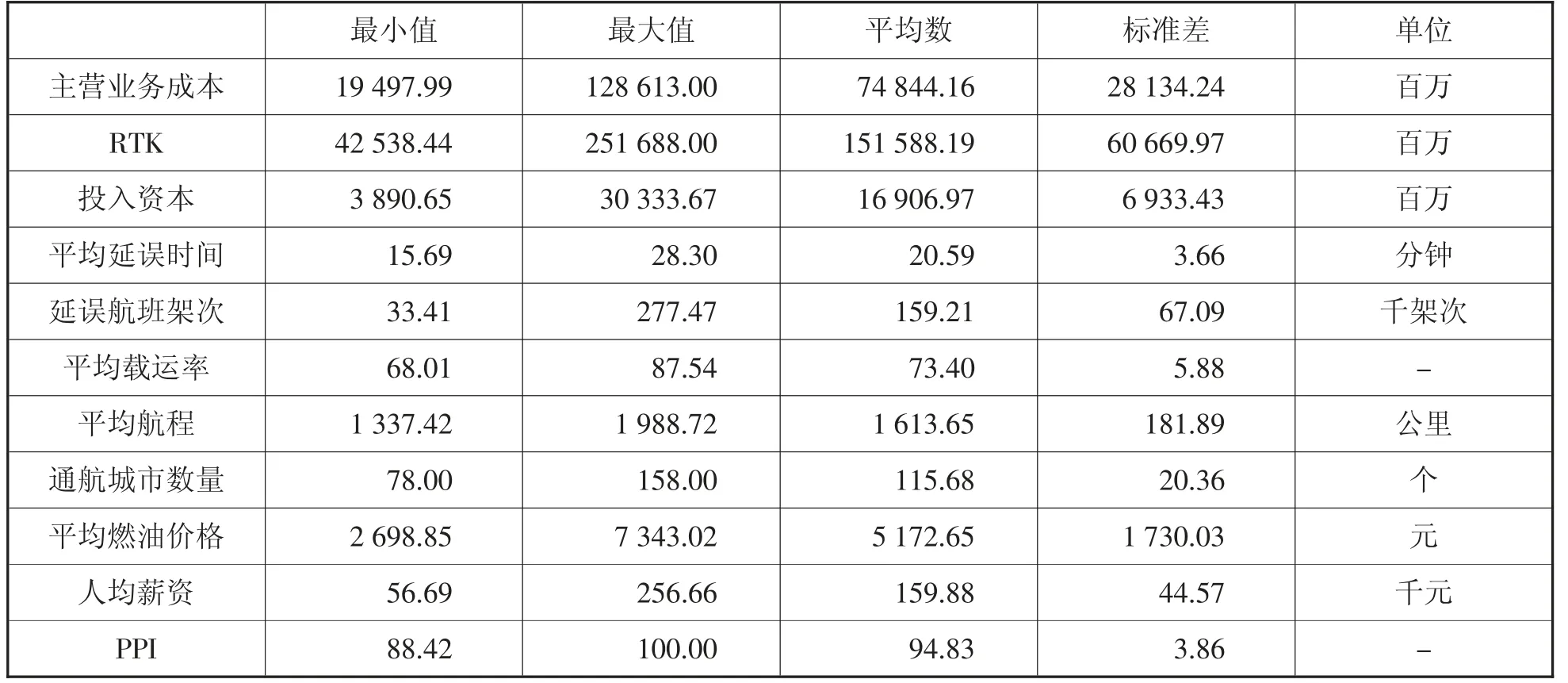
表2 变量描述性统计

4 航空公司航班延误损失测算

本文建立的Trans-log 模型求解是基于公式（1） 和公式（3） 联立方程组，而在实际的数据搜集过程中会出现同一航空公司前后年份数据不全、不同航空公司数据口径不一致等问题，因此本文统计搜集了2014 年至2018 年4 个主要航空公司5 年共计20 个样本（4 个截面单位的5 年数据）。因为Trans-log 成本函数是由Cobb-Douglas 成本函数利用泰勒级数的二阶展开式推导出，以取得更高的近似精度。因此，在本文数据量有限的情况下采取一阶展开式对模型进行拟合。

运用EViews10 软件建立4 个航空公司2014 年至2018 年的面板数据，运用似无关回归对模型进行拟合。取a=0.05，在模型拟合结果中去掉了t-统计量不显著的平均航程和员工平均薪资两个解释变量，之后再次尝试拟合，最终建立的Trans-log 成本函数模型回归结果如表3 所示。

表3 似不相关回归（SUR） 结果

除了延误架次以外所有纳入的变量均取其对数值，为了使延误架次能够取值为0，因此取其状态值纳入。最终模型的R2为0.985，具有相当高的解释力，证明了Trans-log 成本函数模型具有相当强的理论基础，在样本量较少的情况下仍然能够有着相当高的拟合精度。

表3 中的所示解释变量均通过了5%显著性检验，说明航空公司主营业务成本与收入吨公里、投入资本、平均载运率、通航城市数量、燃油和PPI 指数有着显著的相关性。最终构建如式（4） 的航空公司成本函数模型：

当航空公司在其他变量保持不变时，收入吨公里每提高1%其成本提高0.706%；投入资本每提高1%时其成本提高0.09%；当航班平均载运率每提高1%其成本降低0.542%；当通航城市数量每提高1%其成本增加0.242%。模型中关于航班延误架次的系数则表明延误的航班架次每增加1 千架次，其主营业务成本则增加0.0521%。

将航班延误架次降低至0 时，保持其他变量不变，可测算出在无延误情况下航空公司主营业务成本数值，航班延误引起航空公司的损失即为：

根据以上模型，测算得到2018 年航班延误共计给国内4 大主要航空公司带来的成本增加约720.93 亿，占当年主营业务成本的17.76%。2014 年至2018 年航班延误成本及其占总成本比例结果如图2 所示。

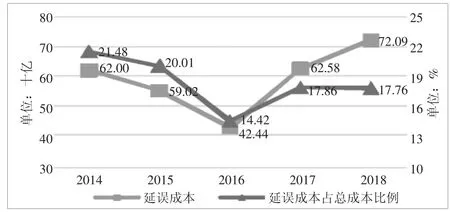
图2 2014～2018 年航班延误成本及其占总成本比例

5 结论与建议

本文通过构建航班延误的Trans-log 成本函数模型并引入延误航班架次作为解释变量之一，间接地测算了航班延误对航空公司的影响。2018 年航班延误对我国4 家主要航空公司合计造成的成本增加达720.93 亿元。由于延误成本是通过增加航油、人工成本等项目隐性的增加，因此更容易被忽视。总结全文可以得出如下结论：

（1） 降低延误成本为航空公司节约运营成本提供了一个有吸引力的潜在途径。如能有效降低此项成本，对于航空公司节约成本提升盈利能力意义重大。

（2） 航班正常率与延误成本/主营成本之间表现出一定的反向关系。对比图1 和图3 有关航班正常率和延误成本占主营成本比率的数据，正常率相对较高的年份，其延误成本占主营成本的比例较低。这意味着航空公司提高航班正常率有助于降低延误成本。

（3） 降低航班延误成本是一个系统工程，需要各方协调运作和软硬件共同投入。降低航班延误需要加强民航监管机构、航空公司、机场、空管，甚至空军的协调沟通，进一步提升管理水平[16-19]。